Praktičan rad
matematike
1. Pronalaženje granice funkcije. Prvo i drugo su divne granice.
2. Derivat kompleksne funkcije. Proučavanje funkcije jedne varijable i crtanje grafova.
3. Test “Primjena diferencijalnog računa na proučavanje funkcija.”
4. Pronalaženje neodređenih integrala. Izračunavanje određenih integrala.
5. Izračunavanje determinanti.
6. Rješavanje sistema linearnih jednačina Cramerovom metodom. Test.
7. Rješavanje zadataka na temu “Skupovi”. Formule logičke algebre.
8. Proračun vjerovatnoće slučajnih događaja. Formula ukupne vjerovatnoće.
9. Proračun numeričkih karakteristika.
10. Test “Osnove teorije vjerovatnoće i matematičke statistike”
11. Trigonometrijski oblik kompleksnog broja.
12. Radnje sa kompleksnim brojevima u raznim oblicima.
METODOLOŠKA UPUTSTVA ZA PRAKTIČNI RAD IZ MATEMATIKE
KURS 2
Praktična nastava je oblik organizovanja obrazovnog procesa koji podrazumijeva izvođenje jednog ili više praktičnih radova učenika po zadatku i pod vodstvom nastavnika.
Tako se u praktičnoj nastavi matematike kod učenika razvija sposobnost rješavanja zadataka, što bi u budućnosti trebalo koristiti za rješavanje stručnih zadataka iz posebnih disciplina.
U toku praktičnog rada studenti ovladavaju sposobnošću korištenja izvora informacija, rada sa regulatornim dokumentima i nastavnim materijalom, priručnikom, izradom crteža, dijagrama, tabela, rješavanjem raznih vrsta zadataka i proračunima.
Zadaci koji se rješavaju na praktičnim časovima matematike:
1) proširenje i učvršćivanje teorijskih znanja iz matematike stečenih na predavanjima;
2) razvijanje kod učenika praktičnih veština i sposobnosti neophodnih za uspešno rešavanje zadataka iz matematike;
3) razvijanje potrebe učenika za samoobrazovanjem i usavršavanjem znanja i veština u procesu izučavanja matematike;
4) formiranje kreativnog stava i istraživačkog pristupa u procesu izučavanja matematike;
5) formiranje profesionalno značajnih kvaliteta budućeg specijaliste i veština primene stečenih znanja u stručnoj oblasti.
Praktična lekcija br. 1. Proračun granica funkcije. Prvo i drugo su divne granice.
Predmet : Proračun granica funkcije.
Cilj: sticanje osnovnih znanja iz oblasti osnovnih grana matematike . Testiranje asimilacije znanja na izračunavanju granica funkcija. Ponoviti i sistematizovati znanje o ovoj temi.
Zadaci:
Razvoj kreativnog profesionalnog mišljenja;
Ovladavanje jezikom nauke, vještine upravljanja konceptima;
Ovladavanje vještinama postavljanja i rješavanja problema;
Produbljivanje teorijske i praktične obuke;
Razvoj inicijative i samostalnosti učenika.
Jačanje računarskih vještina;
Nastavite sa radom na matematičkom govoru.
Formiranje vještina za samostalan rad, rad sa udžbenikom, vještina za samostalno sticanje znanja;
Razvoj sposobnosti isticanja glavne stvari pri radu s tekstom;
Formiranje samostalnog mišljenja, mentalne operacije: poređenje, analiza, sinteza, generalizacija, analogija;
Ukazati učenicima na ulogu sistematskog rada na produbljivanju i jačanju znanja, o kulturi izvršavanja zadataka;
Razvoj kreativnih sposobnosti učenika.
Pružanje praktičnog rada:
Teorijski materijal metodoloških preporuka za praktičan rad.
Matematika, – Serija: Srednje stručno obrazovanje. - Rostov na Donu “Feniks”, str.
Napredak praktične nastave.
1.Formulacija teme časa, objašnjenje povezanosti teme sa drugim temama nastavne discipline;
2.Provjera spremnosti učenika za nastavu;
3. Izvođenje samog časa prema temi iu skladu sa programom rada discipline:
Proučite teorijski materijal na temu „Izračunavanje granica funkcija“.
Razmotrite primjere rješavanja tipičnih zadataka.
Uradite samostalan rad na izračunavanju granica funkcija koristeći prvu i drugu izuzetnu granicu.
Odgovorite na sigurnosna pitanja.
Teorijske informacije i metodološke preporuke
o rješavanju problema.
1. Prezentacija teorijskog materijala.
Da biste izračunali granicu funkcije u tački, trebate:
1) Zamijenite umjesto varijable x ono čemu teži x.
2) Ako nakon završetka koraka 1) dobijemo nesigurnost oblika https://pandia.ru/text/78/405/images/image003_6.png" width="19" height="22 src=">i zamijenimo strelica sa minusom: (x-a).
3) Ako nakon završetka koraka 1) dobijemo nesigurnost oblika https://pandia.ru/text/78/405/images/image002_13.png" width="18" height="31 src="> povezane s vrijednostima trigonometrijskih funkcija, moramo koristiti prvu izvanrednu granicu.
Definicija. Prva izuzetna granica se zove granica
https://pandia.ru/text/78/405/images/image007_4.png" alt="$\displaystyle \lim_(x\to0)\dfrac(\sin x)(x)=1. $" width="102" height="52">!}
5) definicija:Druga izuzetna granica zove limit

Broj koji daje ova granica igra veoma važnu ulogu kako u matematičkoj analizi tako iu drugim granama matematike. Broj je pozvan baza prirodnih logaritama ( https://pandia.ru/text/78/405/images/image009_4.png" alt="$ e$" width="11" height="14">показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:!}
![]()
2. Konsolidacija proučenog materijala.
Primjer 1
https://pandia.ru/text/78/405/images/image015_1.png" width="28" height="30 src=">= -4
Koristili smo pravilo 1) i umjesto x zamijenili ono čemu x treba težiti, tj. x=2.
Primjer 2
https://pandia.ru/text/78/405/images/image017_1.png" width="154" height="32 src=">.png" width="21" height="30 src=">= 5
Primjer 3
https://pandia.ru/text/78/405/images/image021_1.png" width="199" height="37 src=">.png" width="137" height="35 src=">. png" width="138" height="24 src=">=3+3=6
Primjer 4
https://pandia.ru/text/78/405/images/image004_7.png" width="22" height="31 src=">.png" width="104" height="46 src=">. png" height="30 src=">
Primjer 5
https://pandia.ru/text/78/405/images/image032_0.png" width="61" height="46 src=">.png" height="30 src=">=2
Primjer 6
https://pandia.ru/text/78/405/images/image036_0.png" width="18" height="28 src=">
b) 
V) 
3. Konsolidacija znanja, vještina i sposobnosti.
Samostalan rad na izračunavanju granica funkcija.
Praktični rad br.1. Opcija 1 Izračunajte granicu funkcije: 1. 2. 3. 10. | Praktični rad br.1. Opcija 2 Izračunajte granicu funkcije: 1. 2. 3. 10. |
Praktični rad br. 2.
Predmet : Pronalaženje derivacije funkcije. Proučavanje funkcije jedne varijable i crtanje grafa.
Target : U praksi provjeriti poznavanje pojma izvoda funkcije, sposobnost pronalaženja izvoda elementarnih funkcija, složenih funkcija, inverznih funkcija, korištenjem tablice derivacija i pravila diferencijacije, pojma kompleksne i inverzne funkcije, sposobnost koristiti derivat za proučavanje funkcija.
Pružanje praktičnog rada:
Udžbenik. "Matematika". – M.: Drfa, 2010.
Matematika. M: Forum-Infa 2008.
Individualne kartice sa mogućnošću praktičnog rada.
1. Teorijski materijal i primjeri nalaženja derivacije funkcije.
definicija: Derivat funkcije f(x) (f"(x)) u tački x je granica omjera prirasta funkcije i prirasta argumenta kada inkrement argumenta teži nuli:
https://pandia.ru/text/78/405/images/image061_0.png" width="209 height=235" height="235">
Pravila diferencijacije.
Ako funkcije f(x) i g(x) imaju izvode, onda
2. (u+v)′=u′+v′
3. (uv)′=u′v+v′u
4. (C u)′=C u′, gdje je C=konst
5..png" width="49" height="54 src=">
6. Derivat kompleksne funkcije:
f′(g(x))=f′(g) g′(x)
2. Primjeri.
1..png" width="61" height="41 src=">.png" width="20" height="41 src=">.png" width="20" height="41 src="> .png" width="69" height="41 src=">+4).
Funkcija je proizvod dva faktora: u=https://pandia.ru/text/78/405/images/image071_0.png" width="72" height="41 src=">.png" width=" 64" height="41 src=">.png" width="19" height="41 src=">.png" width="45" height="51 src=">.
Funkcija je kvocijent dvaju izraza: u=https://pandia.ru/text/78/405/images/image079.png" width="52" height="41 src=">..png" width= "215" " height="57 src=">.png" width="197 height=36" height="36">
Rješenje. Nađimo izvod ove funkcije koristeći pravilo diferencijacije složenih funkcija (formula 6):

5. Ako , onda 
6. y = x 3 – 3x 2 + 5x+ 2. Nađimo y "(–1).
y " = 3x 2 – 6x+ 5. Dakle, y "(–1) = 14.
7. Ako y= log x cos x, To y" = (ln x)"cos x+ln x(cos x) " =1/x∙cos x–ln x grijeh x.
Neka je data funkcija. Da biste ga proučili potrebno vam je:
1) Pronađite njen domen definicije. Ako nije previše teško, korisno je pronaći i raspon. (Međutim, u mnogim slučajevima, pitanje nalaženja se odlaže dok se ne pronađu ekstremi funkcije.)
2) Saznajte opća svojstva funkcije koja će pomoći u određivanju njenog ponašanja: da li je funkcija parna ili neparna, da li je periodična.
3) Saznajte kako se funkcija ponaša kada se argument približi graničnim tačkama domene definicije, ako postoje takve granične tačke. Ako funkcija ima tačke diskontinuiteta, tada i ove tačke treba provjeriti na prisutnost vertikalnih asimptota funkcije. Pronađite kose asimptote.
4) Pronađite presečne tačke grafa sa koordinatnim osama, što se sastoji od jednostavnog izračunavanja vrednosti funkcije pod uslovom:
Sa OX osom: y=0;
Sa OY osom: x=0.
Pronalaženje točaka presjeka sa osom može dovesti do potrebe rješavanja složene algebarske jednadžbe, što se, možda, može učiniti samo približno. Nakon što smo pronašli korijene funkcije i točke diskontinuiteta, možemo odrediti predznak funkcije u svakom od intervala između ovih tačaka. Ovo se može učiniti ili izračunavanjem vrijednosti funkcije u bilo kojoj tački intervala ili korištenjem metode intervala.
5) Pronađite intervale monotonosti. Da biste to učinili, pronađite izvod i riješite nejednakost:
https://pandia.ru/text/78/405/images/image089.png" width="49" height="19 src=">, funkcija se smanjuje.
Nakon što smo pronašli intervale monotonosti, odmah možemo odrediti točke lokalnog ekstremuma: gdje se povećanje zamjenjuje smanjenjem, nalaze se lokalni maksimumi, a gdje je smanjenje zamijenjeno povećanjem, nalaze se lokalni minimumi.
6) Pronalaženje intervala konveksnosti i konkavnosti vrši se pomoću druge derivacije..png" width="39" height="19 src="> na intervalima:
ako je https://pandia.ru/text/78/405/images/image090.png" width="39" height="19 src=">‹0, tada je kriva grafa funkcije konveksna.
U isto vrijeme, definiramo točke pregiba kao one tačke u kojima funkcija mijenja smjer konveksnosti (i kontinuirana je).
7) Pronalaženje tačaka preseka grafa sa asimptotom i dodatnim tačkama. Ova tačka nije obavezna, ali pronalaženje takvih tačaka čini proučavanje funkcije i njenog grafa potpunim i potpunim.
Imajte na umu da je korisno odmah ucrtati tačke na koordinatne ose i na graf koji se dobijaju tokom proučavanja funkcija na crtežu. Ovo pomaže u razumijevanju izgleda grafa na putu.
3. Uradite sami:
|
opcija | Pronađite izvod funkcije y: |
opcija | Pronađite izvod funkcije y: |
1.y=6- | 1. y=-6- 5.y= |
||
1. y=-7-1 | 1. y=-7-1 |
||
1.y=4x-3tgx+6x-8 | 1.y=-5x+2ctgx+3x-2 |
||
Ciljevi lekcije:
Obrazovni- poznaju formule diferencijacije; pravila diferencijacije;
diferencijacija složene funkcije; fizičko i geometrijsko značenje derivacije;
jednadžba tangente na graf funkcije.
razvojni - biti u stanju pronaći derivate funkcija; rješavati probleme koristeći fizičko značenje, geometrijsko značenje; pronaći vrijednost derivacije funkcije u tački; matematički ispravno objasniti i opravdati izvršene radnje.
edukativni – negovati nezavisnost, odgovornost, promišljanje.
Tokom nastave
I. Organizacioni momenat.
II. Provjera domaćeg
(za vrijeme odmora konsultanti provjeravaju (učenike) i dodjeljuju ocjene).
III. Postavljanje ciljeva i motivacija
Nastavnik obavještava učenike da je ovaj čas završni čas na temu „Izračunavanje izvoda“ i poziva ih da sami formulišu svoje ciljeve.
Učitelj: „Veliki filozof Konfučije je jednom rekao: „Tri puta vode do znanja: put razmišljanja je najplemenitiji put, put oponašanja je najlakši put, a put iskustva je najgorči put.” Tako će danas na času svako od vas odrediti na kom se putu do znanja o ovoj temi nalazi.”
Učenicima se daje zadatak da pokažu svoje znanje i vještine u računanju izvedenica i dobijaju plan časa.
I faza: Dovršavanje zadatka pomoću kartice "Zapamti".
(provjera znanja formula i pravila diferencijacije).
II faza: Usmeni frontalni rad na ponavljanju i generalizaciji znanja.
III faza:“Probna prognoza” (prilikom obavljanja ovog zadatka, pomoć konsultanata je prihvatljiva).
IV. faza: Rješenje praktičnog problema.
V. faza: Samostalan rad
Ocjenjuju se I, III, V faze rada i domaće zadaće. Konsultanti provjeravaju i unose rezultate u tabelu evaluacije.
Kriterijumi ocjenjivanja: "5"- 19-20 bodova;
"4"- 15-18 bodova;
"3"- 10-14 poena.
Putevi do znanja
- Reprodukcija i korekcija referentnog znanja
Faza I.
Cilj: kontrola, samokontrola znanja formula i pravila diferencijacije
Zapamtite! F.I. ___________________________________________________ |
|
Derivat |
|
c,c - kontra t |
|
|
|
|
|
f"(x)+ g"(x) |
|
f(x)* g(x) |
|
|
|
Na kraju ovog zadatka vrši se samotestiranje pomoću „Tabele izvedenica“. Kartice se predaju konsultantima na verifikaciju (ispravke na karticama nisu dozvoljene).
V. Generalizacija i sistematizacija znanja
Faza II.
1. Oralni frontalni rad.
A. Generirajte zadatak za ovaj uslov i riješite ga.
![]()
1. Pronađite vrijednost izvoda funkcije u tački t = 3. (Odgovor: 21.)
2. Napravite jednačinu za tangentu na graf funkcije u tački t = 3. (Odgovor: y = 21x-45.).
3. Odrediti brzinu tijela i ubrzanje u trenutku t=3c, ako je zakon kretanja dat formulom. (Odgovor: 21 m/s, 16 m/s²).
4. Odrediti ugaoni koeficijent tangente povučene na graf funkcije u tački t = 3. (Odgovor: 21.).
5. Naći tangentu ugla nagiba tangente na graf funkcije u tački t = 3 i odrediti vrstu ugla između tangente i pozitivnog smjera ose Ox. (Odgovor: tgα, ugao α je oštar)
B. Pronađite izvode funkcija

2. Faza III“Test prognoza”


Na kraju ovog zadatka vrši se samotestiranje na osnovu konačnih odgovora i testovi se predaju konsultantima. (ispravke na karticama nisu dozvoljene).
odgovori:
1 opcija |
||||
Opcija 2 |
- Rješenje problema
IFaza V
Frontalno rješenje problema naprednog nivoa (rješenje sprovode konsultanti zajedno sa razredom).
Zadatak
Na kojim vrijednostima parametara a tangente na graf funkcije ![]()
nacrtane u tačkama njegovog preseka sa X osom, formiraju ugao od 60° između sebe?

Graf je parabola sa granama nagore koje sijeku os X u dvije tačke (slučaj a=0 ne zadovoljava značenje problema):
IX. Sumiranje i ocjenjivanje
1. Pitanja: a) Da li je svrha lekcije postignuta?
b) Koja faza je izgledala najteža?
c) Šta je bilo najzanimljivije?
2. Konsultanti objavljuju rezultate (broj i imena učenika na putu
imitacija, načini refleksije i načini iskustva).
Praktična lekcija
Predmet: Pronalaženje derivata. Primjena derivacije u proučavanju funkcija i crtanju grafova.
Cilj: Savladajte izračunavanje izvoda, naučite istraživati funkciju koristeći izvod
Sredstva obrazovanja: sveske za praktične vježbe, prezentacije na temu, internet resursi.
1. Razmotriti teorijski materijal na teme: „Pravila za računanje izvoda“, „Ekstremum funkcije“, „Konveksnost, konkavnost. Prevojna tačka."
2. Pregledajte uzorke zadataka.
3. Odraditi testni zadatak br.
Kontrolna pitanja:
1. Definirajte maksimum (minimum) funkcije u tački. Šta se može reći o predznaku prirasta funkcije u prilično maloj okolini maksimalne (minimalne) tačke?
2. Koji su uslovi neophodni za postojanje ekstremuma funkcije? Koje je njihovo geometrijsko značenje?
3. Koje je pravilo za pronalaženje najveće i najmanje vrijednosti funkcije na segmentu?
4. Definirati konveksnost (konkavnost) krive na intervalu.
5. Koje je pravilo za pronalaženje intervala konveksnosti i konkavnosti krive?
6. Prevojna tačka krive. Kako je pronaći?
7. Koji je algoritam za konstruisanje grafa funkcije?
Pravila za obračun derivata
Derivat kompleksne funkcije.
Ako at=ƒ( I), u=φ(x), onda at¢ ( X)=ƒ¢ (i)·φ¢ (X).
Derivat sume.
Ako at(X)=I(X)+v (X), To at¢ (X)=I¢ (X)+v ¢ (X)
Derivat proizvoda.
Ako y(x)=u(X)· v (X), To at¢ = I¢ · v + u · v ¢ .
Konkretno, ( With· i)¢ =c· I¢, tj. konstantni faktor je uzet ispod predznaka derivacije. Lako je to provjeriti
(u 2 ) ¢ = 2 u·u ¢ , (u 3 ) ¢ =3u 2 u ¢ , … , (u n ) ¢ =n·u n–1 u ¢ .
Derivat količnika.
Ako onda  .
.
Tabela derivata
1. (sa)¢ =0
Za složenu funkciju: if u=u(x), To:
2. (X)¢ =1
3. (X α )¢ = α · Xα–1, A– bilo koji realan broj.
 .
.
3. 

4. (A X ) ¢ =a X · ln A
4. 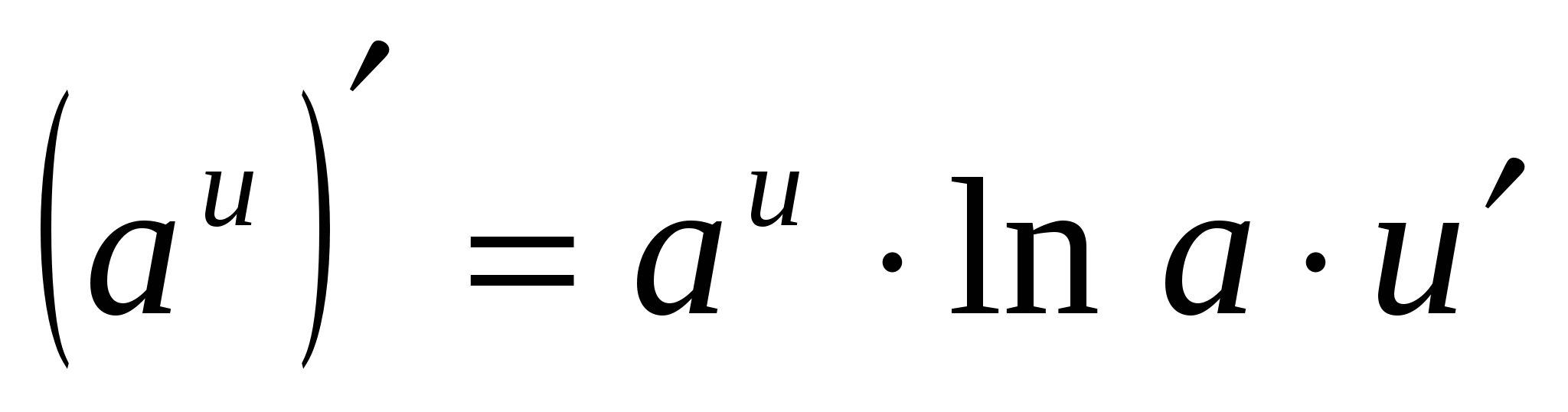

5. (log
a
x)
¢
=
 .
.
5. 

6. (grijeh x)¢ =cos x
6. 
7. (cos x)¢ = –sin x
7. 
8. (tg x)¢
=
8. 
9. (ctg x)¢
=
9. 
10. 
10. 
11. 
11. 
12. 
12. 
13. 
13. 
Pregledajte primjere
Primjer 1.
y=(3–2 sin 5x ) 4 | Primjenjujemo derivacijske formule za I α ,sin u |
y ¢ =4·(3–2·sin5x) 3·(3–2sin5x) ¢ =4·(3–2·sin5x) 3 ·(0–2·cos5x·5) = –40·(3–2·sin5x) 3 .
Primjer 2.
. 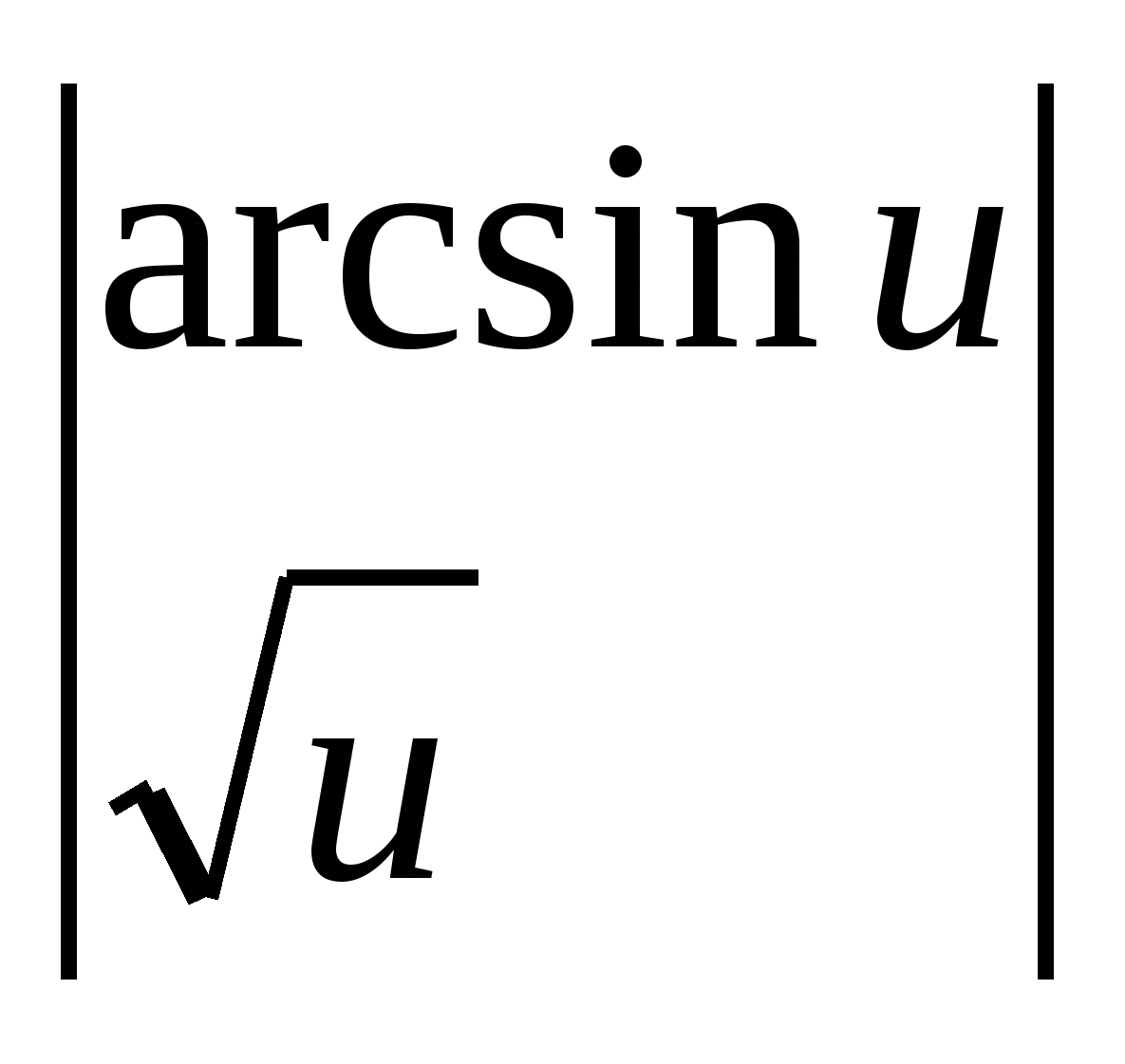

Primjer 3.
 .
. 

Primjer 4.



Primjer 5.
 .
. 

Ekstremum funkcije
Proučavanje funkcije na ekstremumu jedna je od najvažnijih primjena derivacija. Pogledajmo definiciju minimuma i maksimuma i kako ih pronaći.
Neka je funkcija ƒ( X) je definiran i diferencibilan na određenom skupu i tački X 0 je tačka unutar njega.
Definicija. Funkcija ƒ (X) u tački X 0 ima maksimum(minimum), ako postoji takva okolina tačke X 0, što je za sve X sa ovog područja ƒ (X) < ƒ (X 0 ) (ƒ (X) > ƒ (X 0 )).
Dot X 0 se tada naziva tačka maksimum(minimum).

Rice. 1.
Prikazan je graf funkcije koja ima dvije maksimalne točke ( X 1 i X 3) i dva minimalna boda ( X 2 i X 4), a maksimalna vrijednost može biti manja od minimalne ( ƒ (X 1 ) < ƒ (X 4)). Ovo naglašava činjenicu da karakteriziramo singularnost funkcije samo blizu određene točke.
Vrijednosti funkcije u tačkama maksimuma i minimuma nazivaju se ekstremne vrijednosti ili ekstremi. Gornji grafikon pokazuje da tačke ekstrema ( X 1 , X 2 , X 3 , X 4) odrediti intervale monotonosti funkcije u kojima derivacija zadržava određeni predznak. U tačkama ekstrema, naravno, izvod ide na nulu. Hajde da formulišemo teoremu o neophodno stanje postojanje ekstremuma.
Teorema. Ako je funkcija ƒ (X) u tački X 0 ima ekstrem, tada je derivacija funkcije u ovoj tački jednaka nuli, tj. ƒ¢ ( X 0)=0.
Odmah da primetimo da ovaj uslov nije dovoljan, tj. obrnuti iskaz nije uvek tačan. Od jednakosti ƒ ¢ ( X 0)= 0 ne mora nužno pratiti to u tački X 0 postoji ekstrem.
To potvrđuje primjer s funkcijom ƒ (X)=x 3 .
Naći ćemo ƒ ¢ ( X)= 3X 2 . U tački X=0 ƒ ¢ (0)=0 . Ali koliko god želite X=0 ćemo naći X> 0, gde ƒ (X)=x 3 > 0, naći ćemo X< 0, где ¦ (X)=X 3 < 0. Т. е. не существует какая-либо малая окрестность точки X=0, gdje za sve X vrijednost funkcije u tački X=0 će biti najveći ili najmanji. Stoga tačka X=0 nije tačka ekstrema.
Može se i drugačije raspravljati. Pošto je derivat ƒ ¢ (x)=3x 2 , zatim funkciju ƒ(x)=x 3 raste za bilo koji realni x i nema ekstrema.
Tačke u kojima je zadovoljen neophodan ekstremni uslov (ƒ ¢ (x)=0) su pozvani kritičan .
Očigledno, tangenta na graf funkcije u tačkama gdje je ƒ ¢ (x)=0, paralelno sa x-osom Ox .
Dovoljno stanje ekstrem je dat u sljedećim teoremama.
Teorema 1. Ako X 0 je kritična tačka funkcije i pri prolasku kroz nju derivacija mijenja predznak X 0 je tačka ekstrema, naime, ako derivacija promijeni predznak sa plus na minus, to je tačka maksimuma, a ako promijeni predznak sa minusa na plus, to je minimalna tačka.
Imajte na umu da nema ekstremuma u tački ako derivacija ne promijeni predznak. Iz školskog kursa je poznato pravilo za proučavanje ekstremuma pomoću prve izvedenice. Ponekad je zgodnije formulisati dovoljan uslov za ekstrem koristeći drugi izvod.
Neka je funkcija ƒ( X) je dvaput diferencibilan u nekoj domeni (tj. ƒ( X) ima ƒ¢ ( X) I ƒ ¢¢ ( X)).
Teorema 2. Ako X 0 – kritična tačka funkcije ƒ(x) i ƒ ¢¢ (X 0 ) > 0 , To X 0 – minimalna tačka, ako ƒ ¢¢ (X 0 ) < 0, то X 0 – maksimalna tačka.
Koristeći drugi izvod, određuje se konveksnost ili konkavnost grafa funkcije.
Konveksnost, konkavnost. Prevojna tačka.
Curve y=ƒ(X) se zove konveksnoth ispod bilo koja od nje tangenta
ƒ ¢¢ ( X) < 0.
Curve y=ƒ(X) se zove konkavna na intervalu ako sve tačke krive leže viši bilo koja od nje tangenta na ovom intervalu. Zatim na ovom intervalu
ƒ ¢¢(x) > 0
Definicija. Prevojna tačka Kriva je tačka u kojoj je sa jedne strane kriva konveksna, a sa druge konkavna.
Na prevojnoj tački ƒ ¢¢ ( X)=0.
Dakle, znak drugog izvoda (kao i znak same funkcije i njenog prvog izvoda) ukazuje na karakteristike grafa funkcije. Pogledajmo ih ponovo.
Ako za svakoga X na intervalu ( A, b) ƒ (X) > 0 (ƒ (X) < 0), tada graf leži iznad (ispod) x-ose.
Ako za svakoga X na intervalu ( A, b) ƒ ¢ ( X) > 0 (ƒ ¢ ( X) < 0), то функция на (A, b) povećava (smanjuje).
Ako za svakoga X na intervalu ( A, b) ƒ ¢¢ ( X) > 0 (ƒ ¢¢ ( X) < 0), то график на (A, b) konkavno (konveksno).
Jednačina ƒ( X)=0 definiše „nule“ funkcije, odnosno tačke preseka grafika sa Ox osom.
Jednačina ƒ ¢ ( X)=0 definira kritične tačke.
Jednačina ƒ ¢¢ ( X)=0 definira moguće točke pregiba.
Shema proučavanja funkcija
Za proučavanje funkcije ƒ (X) i crtanje y=ƒ(X) treba pronaći:
1) domen definicije funkcije i tačka preseka grafika sa koordinatnim osama;
2) intervali monotonije;
3) tačke ekstrema i vrednosti funkcije u tim tačkama;
4) intervali konveksnosti i konkavnosti grafa;
5) prevojne tačke grafika;
6) konstruisati u Dekartovom koordinatnom sistemu sve dobijene tačke (ponekad se, radi pojašnjenja grafika, dobijaju dodatne tačke) i sam graf.
Najmanje i najveće vrijednosti funkcije na segmentu
Prilikom rješavanja nekih problema optimizacijske metode važno je moći pronaći najmanju ili najveću vrijednost funkcije na određenom segmentu. Funkcija postiže ove vrijednosti ili na kritičnim tačkama ili na krajevima segmenta.
Šema pretraživanja najmanja i najveća vrijednost funkcije ƒ (X) na segmentu [ A, b].
1. Pronađite izvod funkcije ƒ ¢ ( X).
2. Pronađite kritične tačke iz jednačine ƒ ¢ ( X)=0.
3. Odaberite one kritične tačke koje pripadaju ovom segmentu [ A, b] i pronađite vrijednost funkcije ƒ (X) u svakoj takvoj tački.
4. Izračunajte vrijednosti funkcije ƒ (X) na krajevima segmenta: ƒ( A) i ƒ( b).
5. Iz dobivenih vrijednosti funkcije odabrati najveću (najveću) i najmanju (najmanju).
Primjer 2.
Pronađite najveću i najmanju vrijednost funkcije ƒ(x)=X 3 –9x 2 +24h–10 na segmentu.
1. ƒ ¢ ( X)= 3X 2 – 9·2 X 2 + 24.
2. ƒ ¢ ( X)=0, 3(X 2 –6X+8)=0, X 1 =2, X 2 =4.
3. Tačka x 2 =4 ne pripada segmentu. Stoga izračunavamo vrijednost funkcije samo u tački X 1 =2
ƒ(2)=2 3 –9·2 2 +24·2–10=10.
4. Vrijednosti funkcije na krajevima segmenta: ƒ(0)= –10, ƒ(3)=3 3 –9·3 2 +24·3–10, ƒ(3)=8.
5. Dobijene vrijednosti:
ƒ(2)=10, ƒ(0)= –10, ƒ(3)=8.
Najveća vrijednost je 10 i dostiže se u tački X=2. Najmanji je jednak –10 i postiže se u tački X=0.
Primjer 3.
Naći intervale konveksnosti i konkavnosti i pregibne tačke krivulje y=x+36X 2 –2X 3 –X 4 .
Područje definicije ove funkcije je skup svih realnih brojeva, tj. XЄ(–∞, +∞).
Nađimo drugi izvod.
at¢ =1+72 X–6X 2 –4X 3 .
at¢¢ =72–12 X–12X 2 = –12(X 2 +X–6).
Iz Eq. at¢¢ =0 dobijamo apscisu prevojne tačke:
–12(X 2 +X–6)=0 X 1 = –3; X 2 =2.
Hajde da definišemo znak at¢¢ na intervalima
(–∞; –3), (–3; 2), (2, +∞).
X
(–∞, –3)
(–3; 2)
(2; +∞)
at¢¢
oblik krive
konveksan
fleksija
konkavna
fleksija
konveksan
Nađimo ordinate prevojnih tačaka:
at(–3)=726; M 1 (–3; 726) – prevojna tačka
at(2)=114; M 2 (2; 114) – prevojna tačka.
Na intervalu (–3; 2) kriva je konkavna. Na intervalima (–∞; –3) i (2; +∞) – konveksna.
Uzorci zadataka
Zadatak br. 1.
Pronađite prijelomne točke funkcije i nacrtajte graf

Funkcija ƒ (X) je definiran za sve realne X i kontinuirano je na svakom od naznačenih intervala: (–∞; –1), [–1; 0], (0, +∞). Hajde da istražimo funkciju ƒ (X) za kontinuitet u tačkama X= –1 i X=0.
Da bismo to učinili, pronaći ćemo jednostrane granice u svakoj od ovih tačaka.

Pošto su jednostrane granice različite, onda X = –1 – tačka diskontinuiteta prve vrste.

Jednostrane granice su jednake, tj. u tački x=0 postoji granica funkcije i 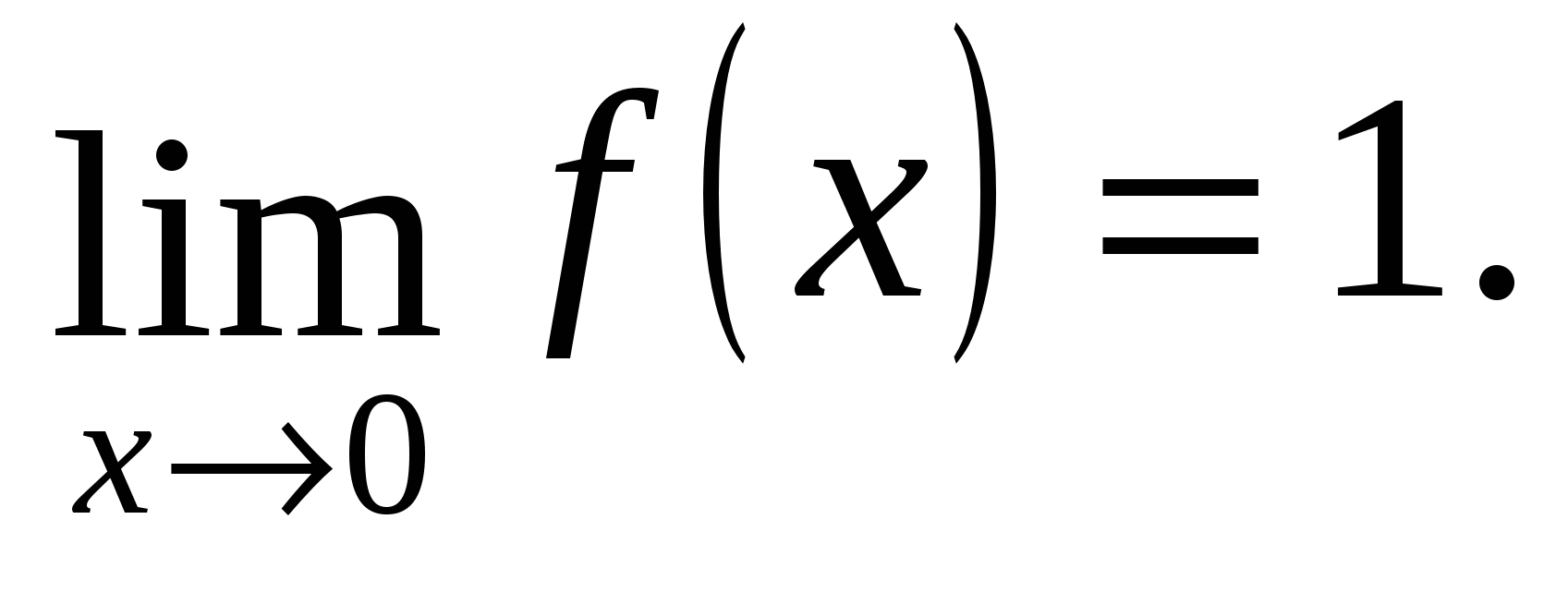
Uporedimo ovu granicu sa vrijednošću funkcije u tački: 
Jer  zatim unutra pri x=0 funkcija ƒ(x) je kontinuirana.
zatim unutra pri x=0 funkcija ƒ(x) je kontinuirana.
Nacrtajmo funkciju ƒ (X), s obzirom na to
1)  – jednačina prave linije,
– jednačina prave linije,
2)  – jednačina gornjeg polukruga
– jednačina gornjeg polukruga  sa centrom u početku i poluprečnikom jednakim jedinici, i pod uslovom –1 £ X£ 0 jednadžba
sa centrom u početku i poluprečnikom jednakim jedinici, i pod uslovom –1 £ X£ 0 jednadžba  definira četvrtinu kruga.
definira četvrtinu kruga.
3) za X > 0 graf je dat jednadžbom  . Tačke preseka ove krive sa Ox osom nalazimo iz jednačine
. Tačke preseka ove krive sa Ox osom nalazimo iz jednačine  za x > 0. x= π
n, Gdje n
=1, 2, 3, 4,
za x > 0. x= π
n, Gdje n
=1, 2, 3, 4,

Rice. 2.
Zadatak br. 2.
Napišite jednadžbe za tangente na pravu  na mestima gde X=0 i X=4. Nađite tačku preseka tangenti i ugao između njih. Napravite crtež.
na mestima gde X=0 i X=4. Nađite tačku preseka tangenti i ugao između njih. Napravite crtež.
Jednadžba tangente na pravu y=ƒ(x) izgleda kao
Gdje at 0 =ƒ( X 0).
U tački X=0 at(0)=ƒ(0)=5.
at¢ =ƒ ¢ (X)=X–3 ƒ¢ (0)= –3.
M 1 (0, 5) ima oblik y– 5= –3(X–0) ili
y= –3X+5.
U tački X=4 at(4)=ƒ(4)=1. ƒ¢ (4)=4–3=1.
Jednačina tangente u tački M 2 (4, 1) ima oblik y– 1=X–4 ili
y=x–3.
Rešavanjem sistema dobijamo tačku preseka tangenti

Tačka raskrsnice M 3 (2, –1).
Ugao φ između tangenti nalazimo iz formule:
 ,
,
Gdje k 1 = –3; k 2 =1 – ugaoni koeficijenti tangenti.
 .
.
Ugao φ =arctg 2.
Hajde da napravimo ovu liniju  – parabola sa vrhom u tački gde X=3, jer at¢
=0 at X=3. Naći ćemo
– parabola sa vrhom u tački gde X=3, jer at¢
=0 at X=3. Naći ćemo  . Dot M 4 (3;
. Dot M 4 (3;  ) je vrh parabole.
) je vrh parabole.
R 
je. 3.
Zadatak br. 3.
Funkcija istraživanja  i zacrtaj.
i zacrtaj.
1. Ova funkcija je polinom (možete otvoriti zagrade, dobijamo polinom trećeg stepena), stoga je definirana, kontinuirana i diferencibilna za bilo koji X.
2. Nađimo izvod.
 .
.
Iz Eq. at¢ =0 hajde da nađemo kritične tačke: 3 X·( X–2)=0, X 1 =0, X 2 =2.
Hajde da ih istražimo.
X
(–∞, 0)
(0; 2)
(2; +∞)
at ¢
at
3. Dakle, funkcija raste na intervalima (–∞, 0) i (2, +∞), opada na intervalu (0; 2), ima maksimum na x=0 i minimum na x=2:
at max = at(0)=4; at min = at(2)=0.
4. Nađimo drugi izvod.
at¢¢ = 6·( X-1).
Kriva je konveksna gdje at¢¢ < 0, т. е. 6·(X–1) < 0, X < 1.
Kriva je konkavna gdje at¢¢ > 0, tj. X > 1.
Dakle, na intervalu (–∞, 1) kriva je konveksna; a na intervalu (1, +∞) je konkavna.
5. Tačku pregiba nalazimo iz jednačine at¢¢ =0. dakle, X=1 – apscisa prevojne tačke, jer ova tačka razdvaja intervale konveksnosti i konkavnosti krive. Ordinata tačke pregiba: at(1)=2.
Grafikon funkcije at=(X+1)·( X–2) 2 siječe os Ox u at=0, tj. kada X= –1 i X=2;
prelazi Oy osu na X=0, tj. kada at=4. Dobili smo tri boda: (–1; 0), (2; 0), (0; 4). Sve dobijene tačke ćemo uneti u tabelu, dodajući i one pored njih.
–2
–1



–16


je. 4 Kriva y=(x+1)(x–2) 2.
Zadatak br. 1
Predstavljamo vam zadatke koji mogu imati jedan, dva, tri ili više tačnih odgovora. Zaokružite brojeve svih tačnih odgovora.
1. Ako  zatim funkciju
zatim funkciju
1) povećanje
2) opadajući
3) konstanta
2. Ako
1) Povećanje
2) Smanjenje
3. Ako  , zatim funkciju
, zatim funkciju
1) Povećanje
2) Smanjenje
4. Ako  , zatim funkciju
, zatim funkciju
1) Raste 3) Opadaju
2) Konstantno 4) Monotono
5. Funkcija  Is
Is
1) Čak
2) Čak ni
3) ni paran ni neparan
4) Periodični
5) Nije periodično
6) Trigonometrijski
7) Osnovno
6. Funkcija  Is
Is
1) čak
2) neparan
3) ni paran ni neparan
4) periodični
5) nije periodično
6) trigonometrijski
7) osnovno
2) Weierstrass 4) Dirichlet 6) Leibniz
8) Rešenje  Jednačine
Jednačine
1) 0 3) 0 i 3 5) 2 7) 3
2) 2 i 3 4) 2 6) -5 i 1 8) 5 i 1
9) rješenje nejednakosti 
1) ( ; 1) 3) (
; 1) 3) ( ; 1) 5) (-
; 1) 5) (- ;1)
;1)
2) (1; 5) 4) (2;  ) 6)
) 6) 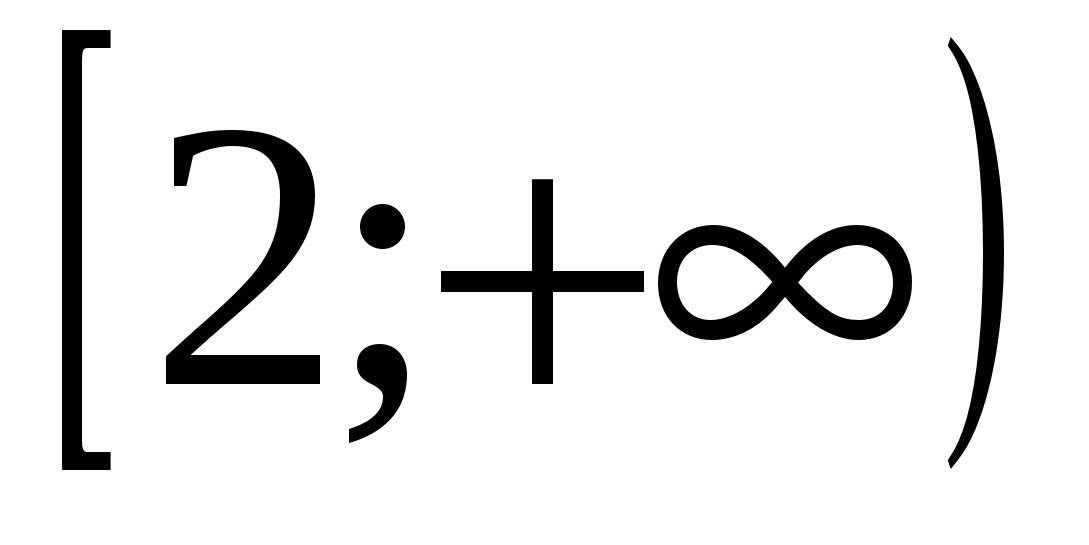
10) Metoda  Iznos je pronađen
Iznos je pronađen
1) vektori
2) ravno
3) segment
11) Ako  , zatim funkciju
, zatim funkciju
1) Konkavno 3) Konveksno 5) Opadajuće
2) Monotono 4) Rastuće 6) Konstantno
12) domen definicije funkcije je jednak 
1) ( ;0)
;0)
2) (0;  )
)
3) (- ;
; )
)
4) (0;1)
5) 
6) 
7) (-1;1)
8) 
9) 
13) funkcija  je
je
1) indikativno
2) trigonometrijski
3) moć
4) logaritamski
14) ako su funkcije y = x  onda je ona
onda je ona 
1) čak
2) neparan
3) ni paran ni neparan
15) funkcija  at
at  je
je

 .
.



