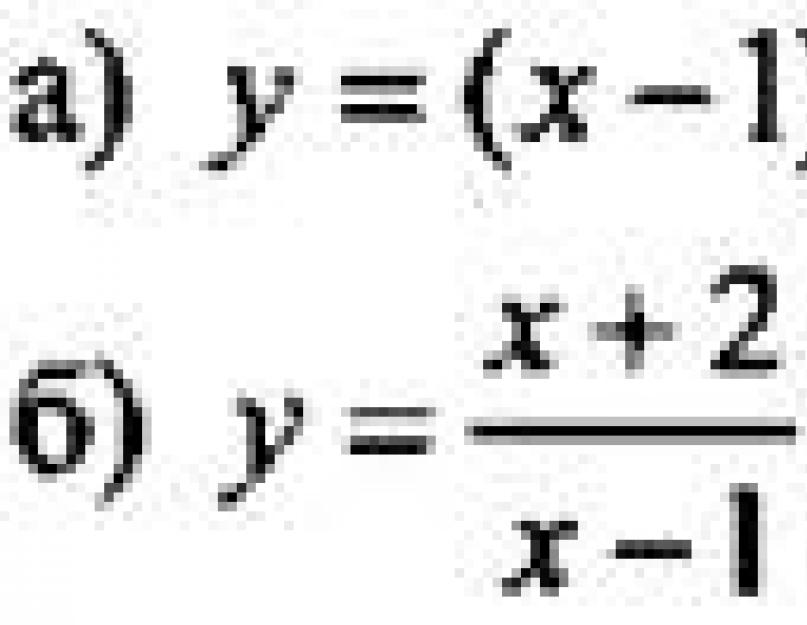Transcriere

1 Conferință științifică și practică regională a lucrărilor educaționale și de cercetare ale elevilor din clasele 6-11 „Aspecte aplicate și fundamentale ale matematicii” Aspecte metodologice ale studierii matematicii Construirea graficelor de funcții care conțin modulul Gabova Angela Yuryevna, clasa a X-a, MOBU „Gimnaziul 3 ” Kudymkar, Pikuleva Nadezhda Ivanovna, profesor de matematică al instituției de învățământ municipal „Gymnasium 3”, Kudymkar Perm, 2016

2 Cuprins: Introducere...3 p. I. Partea principală...6 p. 1.1 Referință istorică.. 6 pagina 2. Definiții de bază și proprietăți ale funcțiilor pagina 2.1 Funcția pătratică.. 7 pagina 2.2 Funcția liniară... 8 pagina 2.3 Funcția fracțională-rațională 8 pagina 3. Algoritmi pentru construirea de grafice cu modulul 9 pagina 3.1 Definirea modulului .. 9 pagina 3.2 Algoritm pentru construirea unui grafic al unei funcții liniare cu un modul...9 pagina 3.3 Construirea graficelor de funcții care conțin „module imbricate” în formula.10 pagina 3.4 Algoritm pentru construirea graficelor funcțiilor de forma y = a 1 x x 1 + a 2 x x a n x x n + ax + b...13 p. 3.5 Algoritm pentru construirea unui grafic al unei funcții pătratice cu modul.14 p. 3.6 Algoritm pentru construirea unui grafic al unei funcții raționale. 15 pp. 4. Modificări ale graficului unei funcții pătratice în funcție de locația semnului valorii absolute..17p. II. Concluzie...26 p. III. Lista referințelor și surselor...27 p. IV. Anexă....28 pagini. 2

3 Introducere Crearea grafică a funcțiilor este una dintre ele cele mai interesante subiecte la matematica scolara. Cel mai mare matematician al timpului nostru, Israel Moiseevich Gelfand, a scris: „Procesul de construire a graficelor este o modalitate de a transforma formulele și descrierile în imagini geometrice. Această reprezentare grafică este un mijloc de a vedea formule și funcții și de a vedea cum se schimbă acele funcții. De exemplu, dacă se scrie y =x 2, atunci vedeți imediat o parabolă; dacă y = x 2-4, vedeți o parabolă coborâtă cu patru unități; dacă y = -(x 2 4), atunci vedeți parabola anterioară respinsă. Această capacitate de a vedea imediat o formulă și interpretarea ei geometrică este importantă nu numai pentru studiul matematicii, ci și pentru alte materii. Este o abilitate care rămâne cu tine de-a lungul vieții, cum ar fi să mergi pe bicicletă, să tastezi sau să conduci o mașină.” Bazele rezolvării ecuațiilor cu module au fost obținute în clasele a VI-a-7. Am ales acest subiect special pentru că cred că necesită o cercetare mai profundă și mai amănunțită. Vreau să dobândesc mai multe cunoștințe despre modulul numerelor, diferite moduri de a construi grafice care conțin semnul valorii absolute. Când semnul modulului este inclus în ecuațiile „standard” de linii, parabole și hiperbole, graficele lor devin neobișnuite și chiar frumoase. Pentru a învăța cum să construiți astfel de grafice, trebuie să stăpâniți tehnicile de construire a figurilor de bază, precum și să cunoașteți și să înțelegeți cu fermitate definiția modulului unui număr. La cursul de matematică din școală, graficele cu modulul nu sunt discutate suficient de aprofundat, motiv pentru care mi-am dorit să-mi extind cunoștințele pe această temă și să-mi fac propriile cercetări. Fără a cunoaște definiția unui modul, este imposibil să construim chiar și cel mai simplu grafic care conține o valoare absolută. Trăsătură caracteristică grafice ale funcțiilor care conțin expresii cu semnul modulului, 3

4 este prezența deformărilor în acele puncte în care expresia sub semnul modulului își schimbă semnul. Scopul lucrării: a lua în considerare construcția unui grafic de funcții liniare, pătratice și fracționale raționale care conțin o variabilă sub semnul modulului. Obiective: 1) Studierea literaturii de specialitate cu privire la proprietățile valorii absolute a liniare, pătratice și fracționar-rațional funcții. 2) Investigați modificările graficelor de funcții în funcție de locația semnului valorii absolute. 3) Învață să grafici ecuații. Obiectul de studiu: grafice ale funcțiilor liniare, pătratice și raționale fracționale. Obiectul cercetării: modificări ale graficului funcțiilor liniare, pătratice și raționale fracționale în funcție de locația semnului valorii absolute. Semnificație practică munca mea este: 1) să folosesc cunoștințele dobândite pe această temă, precum și să le aprofundez și să le aplic altor funcții și ecuații; 2) în utilizarea deprinderilor muncă de cercetareîn viitor activități educaționale. Relevanță: Sarcinile de reprezentare grafică sunt în mod tradițional unul dintre cele mai dificile subiecte din matematică. Noi absolvenții ne confruntăm cu problema promovării cu succes a examenului de stat și a examenului unificat de stat. Problemă de cercetare: construirea graficelor de funcții care conțin semnul modulului din partea a doua a GIA. Ipoteza cercetării: aplicație dezvoltată pe baza metode comune construirea de grafice ale funcțiilor care conțin semnul modulului, metodele de rezolvare a sarcinilor din partea a doua a GIA vor permite elevilor să rezolve aceste sarcini 4

5 în mod conștient, alegeți cea mai rațională metodă de rezolvare, aplicați diferite metode de rezolvare și promovați cu mai mult succes examenul de stat. Metode de cercetare utilizate în lucrare: 1. Analiza literaturii matematice și a resurselor de pe Internet pe această temă. 2. Reproducerea reproductivă a materialului studiat. 3. Activități cognitive și de căutare. 4.Analiza si compararea datelor in cautarea solutiilor la probleme. 5. Enunţarea ipotezelor şi verificarea acestora. 6. Comparație și generalizare fapte matematice. 7. Analiza rezultatelor obtinute. La redactarea acestei lucrări s-au folosit următoarele surse: resurse de internet, teste OGE, literatură matematică. 5

6 I. Partea principală 1.1 Context istoric. În prima jumătate a secolului al XVII-lea, a început să apară ideea funcției ca dependență a unei variabile de alta. Astfel, matematicienii francezi Pierre Fermat () și Rene Descartes () și-au imaginat o funcție ca dependența ordonatei unui punct de o curbă de pe abscisa acestuia. Iar omul de știință englez Isaac Newton () a înțeles o funcție ca fiind coordonatele unui punct în mișcare care se schimbă în funcție de timp. Termenul „funcție” (din latinescul execuție a funcției, realizare) a fost introdus pentru prima dată de matematicianul german Gottfried Leibniz(). El a asociat o funcție cu o imagine geometrică (graficul unei funcții). Ulterior, matematicianul elvețian Johann Bernoulli (și membru Academia din Sankt Petersburgștiințe, celebrul matematician al secolului al XVIII-lea Leonard Euler () considera o funcție ca expresie analitică. Euler are, de asemenea, o înțelegere generală a unei funcții ca dependență a unei variabile de alta. Cuvântul „modul” provine de la cuvânt latin„modul”, care înseamnă „măsură”. Acest cuvânt ambiguu(omonim), care are multe semnificații și este folosit nu numai în matematică, ci și în arhitectură, fizică, tehnologie, programare și altele științe exacte. În arhitectură, aceasta este unitatea inițială de măsură stabilită pentru o anumită structură arhitecturală și utilizată pentru a exprima mai multe rapoarte ale acesteia. elemente constitutive. În tehnologie, acesta este un termen folosit în diverse domenii ale tehnologiei, care nu are un sens universal și servește la desemnarea diferiților coeficienți și cantități, de exemplu, modulul de angajare, modulul de elasticitate etc. 6

7 Modulul de volum (în fizică) este raportul dintre efortul normal dintr-un material și alungirea relativă. 2. Definiții de bază și proprietăți ale funcțiilor Funcția este unul dintre cele mai importante concepte matematice. O funcție este o dependență a variabilei y de variabila x, astfel încât fiecare valoare a variabilei x să corespundă unei singure valori a variabilei y. Metode de specificare a unei funcții: 1) metodă analitică (funcția este specificată folosind o formulă matematică); 2) metoda tabulară (funcția este specificată folosind un tabel); 3) metoda descriptivă (funcția este specificată prin descriere verbală); 4) metoda grafica(funcția este specificată folosind un grafic). Graficul unei funcții este mulțimea tuturor punctelor planului de coordonate, ale căror abscise sunt egale cu valoarea argumentului, iar ordonatele sunt egale cu valorile corespunzătoare ale funcției. 2.1 Funcția pătratică O funcție definită prin formula y = ax 2 + in + c, unde x și y sunt variabile, iar parametrii a, b și c sunt orice numere reale, iar a = 0, se numește pătratică. Graficul funcției y=ax 2 +in+c este o parabolă; axa de simetrie a parabolei y=ax 2 +in+c este o linie dreaptă, pentru a>0 „ramurile” parabolei sunt îndreptate în sus, pentru o<0 вниз. Чтобы построить график квадратичной функции, нужно: 1) найти координаты вершины параболы и отметить её в координатной плоскости; 2) построить ещё несколько точек, принадлежащих параболе; 3) соединить отмеченные точки плавной линией.,. 2.2Линейная функция функция вида 7

8 (pentru funcțiile unei variabile). Proprietatea principală a funcțiilor liniare: incrementul funcției este proporțional cu incrementul argumentului. Adică, funcția este o generalizare a proporționalității directe. Graficul unei funcții liniare este o linie dreaptă, de unde provine numele acesteia. Aceasta se referă la o funcție reală a unei variabile reale. 1) Când, linia dreaptă formează un unghi ascuțit cu direcția pozitivă a axei absciselor. 2) Când, linia dreaptă formează un unghi obtuz cu direcția pozitivă a axei x. 3) este indicatorul de ordonate al punctului de intersecție a dreptei cu axa ordonatelor. 4) Când, linia dreaptă trece prin origine. , 2.3 O funcție fracționară-rațională este o fracție al cărei numărător și numitor sunt polinoame. Are forma unde, polinoame în orice număr de variabile. Un caz special sunt funcțiile raționale ale unei variabile:, unde și sunt polinoame. 1) Orice expresie care poate fi obținută din variabile folosind patru operații aritmetice este o funcție rațională. 8

9 2) Mulțimea funcțiilor raționale este închisă sub operațiile aritmetice și operația de compunere. 3) Orice funcție rațională poate fi reprezentată ca o sumă de fracții simple - aceasta este folosită în integrarea analitică.. , 3. Algoritmi pentru construirea de grafice cu modul 3.1 Definiția modulului Modulul unui număr real a este numărul a însuși, dacă este nenegativ, iar numărul opus a, dacă a este negativ. a = 3.2 Algoritm pentru construirea unui grafic al unei funcții liniare cu modul Pentru a construi grafice ale funcțiilor y = x trebuie să știți că pentru x pozitiv avem x = x. Aceasta înseamnă că pentru valorile pozitive ale argumentului, graficul y= x coincide cu graficul y=x, adică această parte a graficului este o rază care iese de la origine la un unghi de 45 de grade față de axa absciselor. . La x< 0 имеем x = -x; значит, для отрицательных x график y= x совпадает с биссектрисой второго координатного угла. Впрочем, вторую половину графика (для отрицательных X) легко получить из первой, если заметить, что функция y= x чётная, так как -a = a. Значит, график функции y= x симметричен относительно оси Oy, и вторую половину графика можно приобрести, отразив относительно оси ординат часть, начерченную для положительных x. Получается график:y= x 9

10 Pentru a construi, luăm punctele (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2). Acum să construim un grafic y= x-1 Dacă A este un punct pe graficul y= x cu coordonatele (a; a), atunci punctul de pe grafic y= x-1 cu aceeași valoare a ordonatei Y. fie punctul A1(a+1; a). Acest punct al celui de-al doilea grafic poate fi obținut din punctul A(a; a) al primului grafic prin deplasarea paralelă cu axa Ox la dreapta. Aceasta înseamnă că întregul grafic al funcției y= x-1 se obține din graficul funcției y= x prin deplasarea paralelă cu axa Ox la dreapta cu 1. Să construim graficele: y= x-1 Pentru a construi , luați punctele (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1). 3.3 Construirea graficelor de funcții care conțin „module imbricate” în formulă Să luăm în considerare algoritmul de construcție folosind un exemplu specific. Construiți un grafic al unei funcții: 10

11 y=i-2-ix+5ii 1. Construiți un grafic al funcției. 2. Afișăm graficul semiplanului inferior în sus simetric față de axa OX și obținem graficul funcției. unsprezece

12 3. Afișăm graficul funcției în jos simetric față de axa OX și obținem graficul funcției. 4. Afișăm graficul funcției în jos simetric față de axa OX și obținem un grafic al funcției 5. Afișăm graficul funcției în raport cu axa OX și obținem un grafic. 12

13 6. Drept urmare, graficul funcției arată astfel 3.4. Algoritm pentru construirea graficelor de funcții de forma y = a 1 x x 1 + a 2 x x a n x x n + ax + b. În exemplul anterior a fost destul de ușor să dezvăluiți semnele de modul. Dacă există mai multe sume de module, atunci este problematic să luăm în considerare toate combinațiile posibile de semne ale expresiilor submodulare. Cum se construiește, în acest caz, un grafic al funcției? Rețineți că graficul este o linie întreruptă, cu vârfuri în puncte având abscisele -1 și 2. La x = -1 și x = 2, expresiile submodulare sunt egale cu zero. În practică, ne-am apropiat de regula pentru construirea unor astfel de grafice: Graficul unei funcții de forma y = a 1 x x 1 + a 2 x x a n x x n + ax + b este o linie întreruptă cu legături extreme infinite. Pentru a construi o astfel de linie întreruptă, este suficient să cunoașteți toate vârfurile acesteia (abscisele vârfurilor sunt zerourile expresiilor submodulare) și un punct de control pe legăturile infinite stânga și dreapta. 13

14 Problemă. Reprezentați grafic funcția y = x + x 1 + x + 1 și găsiți cea mai mică valoare a acesteia. Rezolvare: 1. Zerourile expresiilor submodulare: 0; -1; Vârfurile poliliniei (0; 2); (-13); (1; 3) (substituim zerourile expresiilor submodulare în ecuație) 3 Punct de control în dreapta (2; 6), în stânga (-2; 6). Construim un grafic (Fig. 7), cea mai mică valoare a funcției este Algoritmul pentru construirea unui grafic al unei funcții pătratice cu modulul Elaborarea algoritmilor de conversie a graficelor de funcții. 1. Trasarea unui grafic al funcției y= f(x). Prin definiția unui modul, această funcție este împărțită într-un set de două funcții. În consecință, graficul funcției y= f(x) este format din două grafice: y= f(x) în semiplanul drept, y= f(-x) în semiplanul stâng. Pe baza acesteia se poate formula o regulă (algoritm). Graficul funcției y= f(x) se obține din graficul funcției y= f(x) astfel: la x 0 se păstrează graficul, iar la x< 0полученная часть графика отображается симметрично относительно оси ОУ. 2.Построение графика функции y= f(x). а). Строим график функции y= f(x). б). Часть графика y= f(x), лежащая над осью ОХ, сохраняется, часть его, лежащая под осью ОХ, отображается симметрично относительно оси ОХ. 14

15 3. Pentru a construi un grafic al funcției y= f(x), trebuie mai întâi să construiți un grafic al funcției y= f(x) pentru x> 0, apoi pentru x< 0 построить изображение, симметричное ему относительно оси ОУ, а затем на интервалах, где f(x) <0,построить изображение, симметричное графику y= f(x) относительно оси ОХ. 4.Для построения графиков вида y = f(x)достаточно построить график функции y= f(x) для тех х из области определения, при которых f(х) 0, и отобразить полученную часть графика симметрично относительно оси абсцисс. Пример Построим график функции у = х 2 6х +5. Сначала построим параболу у= х 2 6х +5. Чтобы получить из неё график функции у = х 2-6х + 5, нужно каждую точку параболы с отрицательной ординатой заменить точкой с той же абсциссой, но с противоположной (положительной) ординатой. Иными словами, часть параболы, расположенную ниже оси Ох, нужно заменить линией, ей симметричной относительно оси Ох (Рис.1). Рис Алгоритм построения графика дробно рациональной функции с модулем 1. Начнем с построения графика В основе его лежит график функции и все мы знаем, как он выглядит: Теперь построим график 15

16 Pentru a obține acest grafic, trebuie doar să mutați graficul obținut anterior cu trei unități la dreapta. Rețineți că dacă numitorul fracției conține expresia x + 3, atunci am deplasa graficul la stânga: Acum trebuie să înmulțim toate ordonatele cu două pentru a obține graficul funcției. În cele din urmă, deplasăm graficul în sus două unități: Ultimul lucru pe care trebuie să-l facem este , este să construim un grafic al unei funcții date dacă este închisă sub semnul modulului. Pentru a face acest lucru, reflectăm simetric în sus întreaga parte a graficului ale cărei ordonate sunt negative (acea parte care se află sub axa x): Fig. 4 16

17 4.Modificări în graficul unei funcții pătratice în funcție de locația semnului valorii absolute. Construiți un grafic al funcției y = x 2 - x -3 1) Deoarece x = x la x 0, graficul necesar coincide cu parabola y = 0,25 x 2 - x - 3. Dacă x<0, то поскольку х 2 = х 2, х =-х и требуемый график совпадает с параболой у=0,25 х 2 + х) Если рассмотрим график у=0,25 х 2 - х - 3 при х 0 и отобразить его относительно оси ОУ мы получим тот же самый график. (0; - 3) координаты точки пересечения графика функции с осью ОУ. у =0, х 2 -х -3 = 0 х 2-4х -12 = 0 Имеем, х 1 = - 2; х 2 = 6. (-2; 0) и (6; 0) - координаты точки пересечения графика функции с осью ОХ. Если х<0, ордината точки требуемого графика такая же, как и у точки параболы, но с положительной абсциссой, равной х. Такие точки симметричны относительно оси ОУ(например, вершины (2; -4) и -(2; -4). Значит, часть требуемого графика, соответствующая значениям х<0, симметрична относительно оси ОУ его же части, соответствующей значениям х>0. b) Prin urmare, completez construcția pentru x<0 часть графика, симметричную построенной относительно оси ОУ. 17

18 Fig. 4 Graficul funcției y = f (x) coincide cu graficul funcției y = f (x) pe mulțimea valorilor nenegative ale argumentului și este simetric față de acesta față de axa OU pe setul de valori negative ale argumentului. Dovada: Dacă x 0, atunci f (x) = f (x), adică. pe setul de valori nenegative ale argumentului, graficele funcțiilor y = f (x) și y = f (x) coincid. Deoarece y = f (x) este o funcție pară, graficul său este simetric față de amplificatorul operațional. Astfel, graficul funcției y = f (x) poate fi obținut din graficul funcției y = f (x) astfel: 1. construiți un grafic al funcției y = f (x) pentru x>0; 2. Pentru x<0, симметрично отразить построенную часть относительно оси ОУ. Вывод: Для построения графика функции у = f (х) 1. построить график функции у = f(х) для х>0; 2. Pentru x<0, симметрично отразить построенную часть относительно оси ОУ. Построить график функции у = х 2-2х Освободимся от знака модуля по определению Если х 2-2х 0, т.е. если х 0 и х 2, то х 2-2х = х 2-2х Если х 2-2х<0, т.е. если 0<х< 2, то х 2-2х =- х 2 + 2х Видим, что на множестве х 0 и х 2 графики функции у = х 2-2х и у = х 2-2х совпадают, а на множестве (0;2) графики функции у = -х 2 + 2х и у = х 2-2х совпадают. Построим их. График функции у = f (х) состоит из части графика функции у = f(х) при у?0 и симметрично отражённой части у = f(х) при у <0 относительно оси ОХ. Построить график функции у = х 2 - х -6 1) Если х 2 - х -6 0, т.е. если х -2 и х 3, то х 2 - х -6 = х 2 - х

19 Dacă x 2 - x -6<0, т.е. если -2<х< 3, то х 2 - х -6 = -х 2 + х +6. Построим их. 2) Построим у = х 2 - х -6. Нижнюю часть графика симметрично отбражаем относительно ОХ. Сравнивая 1) и 2), видим что графики одинаковые. Работа на тетрадях. Докажем, что график функции у = f (х) совпадает с графиком функции у = f (х) для f(х) >0 și partea reflectată simetric y = f(x) la y<0 относительно оси ОХ. Действительно, по определению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий: у = f(х), если f(х) 0; у = - f(х), если f(х) <0 Для любой функции у = f(х), если f(х) >0, atunci f (x) = f (x), ceea ce înseamnă că în această parte graficul funcției y = f (x) coincide cu graficul funcției în sine y = f (x). Dacă f(x)<0, то f (х) = - f(х),т.е. точка (х; - f(х)) симметрична точке (х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ "отрицательную" часть графика у = f(х). Вывод: действительно для построения графика функции у = f(х) достаточно: 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс. (Рис.5) 19

20 Fig.5 Concluzie: Pentru a construi un grafic al funcției y= f(x) 1. Construiți un grafic al funcției y=f(x) ; 2. În zonele în care graficul este situat în semiplanul inferior, adică unde f(x)<0, строим кривые, симметричные построенным графикам относительно оси абсцисс. (Рис.6, 7.) 20

21 Lucrări de cercetare privind construirea de grafice ale funcției y = f (x) Folosind definiția valorii absolute și exemplele discutate anterior, vom construi grafice ale funcției: y = 2 x - 3 y = x 2-5 x y = x 2 -2 și trageți concluzii. Pentru a construi un grafic al funcției y = f (x) trebuie să: 1. Construiți un grafic al funcției y = f (x) pentru x>0. 2. Construiți a doua parte a graficului, adică reflectați graficul construit simetric față de amplificatorul operațional, deoarece Această funcție este uniformă. 3. Convertiți secțiunile graficului rezultat situat în semiplanul inferior în semiplanul superior simetric față de axa OX. Construiți un grafic al funcției y = 2 x - 3 (prima metodă de determinare a modulului) 1. Construiți y = 2 x - 3, pentru 2 x - 3 > 0, x >1,5 adică. X< -1,5 и х>1,5 a) y = 2x - 3, pentru x>0 b) pentru x<0, симметрично отражаем построенную часть относительно оси ОУ. 2. Строим у = -2 х + 3, для 2 х - 3 < 0. т.е. -1,5<х<1,5 а) у = -2х + 3, для х>0 b) pentru x<0, симметрично отражаем построенную часть относительно оси ОУ. У = 2 х - 3 1) Строим у = 2х-3, для х>0. 2) Construim o linie dreaptă, simetrică cu cea construită în raport cu axa op-amp-ului. 3) Afișez secțiuni ale graficului situate în semiplanul inferior simetric față de axa OX. Comparând ambele grafice, vedem că sunt aceleași. 21

22 Exemple de probleme Exemplul 1. Se consideră graficul funcției y = x 2 6x +5. Deoarece x este la pătrat, indiferent de semnul numărului x, după pătrat va fi pozitiv. Rezultă că graficul funcției y = x 2-6x +5 va fi identic cu graficul funcției y = x 2-6x +5, adică. graficul unei funcții care nu conține un semn de valoare absolută (Fig. 2). Fig.2 Exemplul 2. Se consideră graficul funcției y = x 2 6 x +5. Folosind definiția modulului unui număr, înlocuim formula y = x 2 6 x +5 Acum avem de-a face cu atribuirea de dependență pe bucăți care ne este familiară. Vom construi un grafic astfel: 1) construim o parabolă y = x 2-6x +5 și încercuim partea care are 22

23 corespunde valorilor nenegative ale lui x, adică. partea situată în dreapta axei Oy. 2) în același plan de coordonate, construiți o parabolă y = x 2 +6x +5 și încercuiți partea care corespunde valorilor negative ale lui x, adică. partea situată în stânga axei Oy. Părțile încercuite ale parabolelor formează împreună un grafic al funcției y = x 2-6 x +5 (Fig. 3). Fig.3 Exemplul 3. Se consideră graficul funcției y = x 2-6 x +5. Deoarece graficul ecuației y = x 2 6x +5 este același cu graficul funcției fără semnul modulului (discutat în exemplul 2), rezultă că graficul funcției y = x 2 6 x +5 este identic la graficul funcției y = x 2 6 x +5 , considerată în exemplul 2 (Fig. 3). Exemplul 4. Să construim un grafic al funcției y = x 2 6x +5. Pentru a face acest lucru, să construim un grafic al funcției y = x 2-6x. Pentru a obține un grafic al funcției y = x 2-6x din aceasta, trebuie să înlocuiți fiecare punct al parabolei cu o ordonată negativă cu un punct cu aceeași abscisă, dar cu ordonată opusă (pozitivă). Cu alte cuvinte, partea parabolei situată sub axa x trebuie înlocuită cu o linie simetrică față de aceasta în raport cu axa x. Deoarece trebuie să construim un grafic al funcției y = x 2-6x +5, apoi graficul funcției pe care am considerat-o y = x 2-6x trebuie doar să fie ridicat de-a lungul axei y cu 5 unități în sus (Fig. 4 ). 23

24 Fig.4 Exemplul 5. Să construim un grafic al funcției y = x 2-6x+5. Pentru a face acest lucru, vom folosi binecunoscuta funcție pe bucăți. Să găsim zerourile funcției y = 6x +5 6x + 5 = 0 la. Să luăm în considerare două cazuri: 1) Dacă, atunci ecuația va lua forma y = x 2 6x -5. Să construim această parabolă și să încercuim partea în care. 2) Dacă, atunci ecuația ia forma y = x 2 + 6x +5. Să stăm această parabolă și să încercuim acea parte a ei care este situată în stânga punctului cu coordonate (Fig. 5). 24

25 Fig.5 Exemplul6. Să construim un grafic al funcției y = x 2 6 x +5. Pentru a face acest lucru, vom construi un grafic al funcției y = x 2-6 x +5. Am construit acest grafic în Exemplul 3. Deoarece funcția noastră este complet sub semnul modulului, pentru a construi un grafic al funcției y = x 2 6 x +5, avem nevoie de fiecare punct al graficului funcției y = x 2 6 x + 5 cu ordonată negativă trebuie înlocuite cu un punct cu aceeași abscisă, dar cu ordonată opusă (pozitivă), adică. partea de parabolă situată sub axa Ox trebuie înlocuită cu o linie simetrică față de aceasta în raport cu axa Ox (Fig. 6). Fig.6 25

26 II. Concluzie „Informația matematică poate fi folosită cu pricepere și cu folos numai dacă este stăpânită în mod creativ, astfel încât elevul să vadă singur cum ar putea ajunge la ea singur.” UN. Kolmogorov. Aceste probleme sunt de mare interes pentru elevii de clasa a IX-a, deoarece sunt foarte frecvente la testele OGE. Abilitatea de a construi grafice de date ale funcțiilor vă va permite să promovați examenul cu mai mult succes. Matematicienii francezi Pierre Fermat () și Rene Descartes () au imaginat o funcție ca dependența ordonatei unui punct de o curbă de pe abscisa acestuia. Iar omul de știință englez Isaac Newton () a înțeles o funcție ca fiind coordonatele unui punct în mișcare care se schimbă în funcție de timp. 26

27 III. Lista referințelor și surselor 1. Galitsky M. L., Goldman A. M., Zvavich L. I. Culegere de probleme de algebră pentru clasele 8-9: Manual. manual pentru elevii școlii. si clase avansate studiat Matematică ed. a II-a. M.: Iluminarea, Dorofeev G.V. Matematică. Algebră. Funcții. Analiza datelor. Clasa a IX-a: m34 Educativ. pentru studii de învăţământ general. stabilire ed. a 2-a, stereotip. M.: Bustard, Solomonik V.S. Culegere de întrebări și probleme de matematică M.: „Școala superioară”, Yashchenko I.V. GIA. Matematică: opțiuni standard de examen: Despre opțiuni.m.: „Educația Națională”, p. 5. Iascenko I.V. OGE. Matematică: opțiuni standard de examen: Despre opțiuni.m.: „Educația Națională”, p. 6. Iascenko I.V. OGE. Matematică: opțiuni standard de examen: Despre opțiuni.m.: „Educația Națională”, cu

28 Anexa 28

29 Exemplul 1. Reprezentați grafic funcția y = x 2 8 x Soluție. Să determinăm paritatea funcției. Valoarea pentru y(-x) este aceeași cu valoarea pentru y(x), deci această funcție este pară. Apoi graficul său este simetric față de axa Oy. Reprezentăm grafic funcția y = x 2 8x + 12 pentru x 0 și afișăm simetric graficul față de Oy pentru negativ x (Fig. 1). Exemplul 2. Următorul grafic de forma y = x 2 8x Aceasta înseamnă că graficul funcției se obține astfel: construiți un grafic al funcției y = x 2 8x + 12, lăsați partea din grafic care se află deasupra axa Ox neschimbată și partea graficului care se află sub axa absciselor și este afișată simetric față de axa Ox (Fig. 2). Exemplul 3. Pentru a reprezenta un grafic al funcției y = x 2 8 x + 12, se efectuează o combinație de transformări: y = x 2 8x + 12 y = x 2 8 x + 12 y = x 2 8 x Răspuns: Figura 3. Exemplul 4 Expresia sub semnul modulului, semnul schimbă în punctul x=2/3. La x<2/3 функция запишется так: 29

30 Pentru x>2/3 funcția se va scrie astfel: Adică punctul x=2/3 împarte planul nostru de coordonate în două zone, în una dintre care (în dreapta) construim o funcție și în cealaltă (la stânga) construim un grafic al funcției: Exemplul 5 Următorul Graficul este și el rupt, dar are două puncte de întrerupere, deoarece conține două expresii sub semnele modulului: Să vedem în ce puncte își schimbă semnul expresiile submodulare: aranjați semnele pentru expresiile submodulare pe linia de coordonate: 30

31 Extindem modulele pe primul interval: Pe al doilea interval: Pe al treilea interval: Astfel, pe intervalul (- ; 1.5] avem un grafic scris de prima ecuație, pe interval un grafic scris de a doua ecuație , și pe interval)