Modele de interacțiune de două tipuri
ipotezele lui Volterra. Analogii cu cinetica chimică. Modele Volterra de interacțiuni. Clasificarea tipurilor de interacţiuni Concurenţă. Prădător-pradă. Modele generalizate de interacțiuni între specii . Modelul Kolmogorov. Modelul lui MacArthur de interacțiune între două specii de insecte. Parametric și portrete de fază ale sistemului Bazykin.
Fondatorul teoriei matematice moderne a populațiilor este considerat pe bună dreptate matematicianul italian Vito Volterra, care a dezvoltat teoria matematică a comunităților biologice, al cărei aparat este ecuațiile diferențiale și integro-diferențiale.(Vito Volterra. Lecons sur la Theorie Mathematique de la Lutte pour la Vie. Paris, 1931). În deceniile următoare, dinamica populației s-a dezvoltat în principal în conformitate cu ideile exprimate în această carte. Traducerea în limba rusă a cărții lui Volterra a fost publicată în 1976 sub titlul: „Teoria matematică a luptei pentru existență” cu o postfață de Yu.M. Svirezhev, care examinează istoria dezvoltării ecologiei matematice în perioada 1931-1976.
Cartea lui Volterra este scrisă așa cum sunt scrise cărțile de matematică. Mai întâi formulează câteva ipoteze despre obiectele matematice care ar trebui să fie studiate, apoi efectuează un studiu matematic al proprietăților acestor obiecte.
Sistemele studiate de Volterra constau din două sau mai multe tipuri. În unele cazuri, se ia în considerare furnizarea de alimente utilizate. Ecuațiile care descriu interacțiunea acestor tipuri se bazează pe următoarele concepte.
ipotezele lui Volterra
1. Alimentele fie sunt disponibile în cantități nelimitate, fie furnizarea lor în timp este strict reglementată.
2. Indivizii fiecărei specii mor în așa fel încât o proporție constantă de indivizi existenți mor pe unitatea de timp.
3. Speciile prădătoare mănâncă victime, iar pe unitatea de timp numărul victimelor consumate este întotdeauna proporțional cu probabilitatea de a întâlni indivizi din aceste două specii, i.e. produsul dintre numărul de prădători și numărul de pradă.
4. Dacă există hrană în cantități limitate și mai multe specii care sunt capabile să o consume, atunci ponderea hranei consumate de o specie pe unitatea de timp este proporțională cu numărul de indivizi ai acestei specii, luate cu un anumit coeficient în funcție de specii (modele de competiție interspecifică).
5. Dacă o specie se hrănește cu hrană disponibilă în cantități nelimitate, creșterea numărului de specii pe unitatea de timp este proporțională cu numărul speciilor.
6. Dacă o specie se hrănește cu hrană disponibilă în cantități limitate, atunci reproducerea acesteia este reglementată de rata consumului de alimente, adică. pe unitatea de timp, creșterea este proporțională cu cantitatea de mâncare consumată.
Analogii cu cinetica chimică
Aceste ipoteze au paralele strânse cu cinetica chimică. În ecuațiile dinamicii populației, ca și în ecuațiile cineticii chimice, se folosește „principiul coliziunii”, când viteza de reacție este proporțională cu produsul concentrațiilor componentelor care reacţionează.
Într-adevăr, conform ipotezelor lui Volterra, viteza proces Dispariția fiecărei specii este proporțională cu numărul speciilor. În cinetica chimică, aceasta corespunde unei reacții monomoleculare de descompunere a unei anumite substanțe, iar într-un model matematic, corespunde unor termeni liniari negativi din partea dreaptă a ecuațiilor.
Conform conceptelor de cinetică chimică, viteza reacției bimoleculare de interacțiune între două substanțe este proporțională cu probabilitatea de coliziune a acestor substanțe, i.e. produsul concentrației lor. În același mod, în conformitate cu ipotezele lui Volterra, rata de reproducere a prădătorilor (moartea prăzii) este proporțională cu probabilitatea întâlnirilor dintre indivizii prădători și pradă, adică. produsul numerelor lor. În ambele cazuri, termenii biliniari apar în sistemul model în partea dreaptă a ecuațiilor corespunzătoare.
În sfârșit, termenii liniari pozitivi din partea dreaptă a ecuațiilor Volterra, corespunzători creșterii populațiilor în condiții nelimitate, corespund termenilor autocatalitici. reacții chimice. Această asemănare a ecuațiilor în modelele chimice și de mediu ne permite să aplicăm aceleași metode de cercetare pentru modelarea matematică a cineticii populației ca și pentru sistemele de reacții chimice.
Clasificarea tipurilor de interacțiune
În conformitate cu ipotezele lui Volterra, interacțiunea a două specii, ale căror numere X 1 și X 2 poate fi descris prin ecuațiile:
(9.1)
Aici sunt parametrii A i - constante ale ritmului de creștere proprie a speciei, c eu- constante de autolimitare a numerelor (competiție intraspecifică), b ij- constantele de interacțiune dintre specii, (i, j= 1,2). Semnele acestor coeficienți determină tipul de interacțiune.
În literatura biologică, interacțiunile sunt de obicei clasificate în funcție de mecanismele implicate. Diversitatea de aici este enormă: diverse interacțiuni trofice, interacțiuni chimice care există între bacterii și alge planctonice, interacțiunile ciupercilor cu alte organisme, succesiunea de organisme vegetale, asociată în special cu competiția pentru lumina soareluişi odată cu evoluţia solurilor etc. Această clasificare pare vastă.
E . Odum, ținând cont de modelele propuse de V. Volterra, a propus o clasificare nu după mecanisme, ci după rezultate. Conform acestei clasificări, relațiile ar trebui evaluate ca pozitive, negative sau neutre, în funcție de faptul că abundența unei specii crește, scade sau rămâne neschimbată în prezența altei specii. Apoi, principalele tipuri de interacțiuni pot fi prezentate sub formă de tabel.
TIPURI DE INTERACȚIUNE ALE SPECIILOR
|
SIMBIOZĂ |
b 12 ,b 21 >0 |
||
|
COMENSALISM |
b 12 ,>0, b 21 =0 |
||
|
PRĂDATOR-VICTICĂ |
b 12 ,>0, b 21 <0 |
||
|
AMENSALISM |
b 12 ,=0, b 21 <0 |
||
|
COMPETIȚIE |
b 12 , b 21 <0 |
||
|
NEUTRALISM |
b 12 , b 21 =0 |
Ultima coloană arată semnele coeficienților de interacțiune din sistemul (9.1)
Să ne uităm la principalele tipuri de interacțiuni
ECUATII DE CONCURS:
După cum am văzut în cursul 6, ecuațiile concurenței sunt:
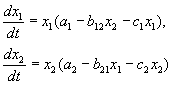 (9.2)
(9.2)
Soluții de sistem staționar:
(1).
![]()
Originea coordonatelor, pentru orice parametri de sistem, este un nod instabil.
(2).
![]() (9.3)
(9.3)
C starea staționară (9.3) este o șa la A 1 >b 12 /Cu 2 și
nod stabil la A 1 12 /s 2 . Această condiție înseamnă că o specie dispare dacă propria sa rată de creștere este mai mică decât o anumită valoare critică.
(3).
![]() (9.4)
(9.4)
C soluție staționară (9.4)¾ şa la A 2 >b 21 /c 1 si un nod stabil la A 2< b 21 /c 1
(4).
![]() (9.5)
(9.5)
Starea staționară (9.5) caracterizează coexistența a două specii concurente și reprezintă un nod stabil dacă relația este satisfăcută:
![]()
Aceasta implică inegalitatea:
b 12
b 21
permițându-ne să formulăm condiția de coexistență a speciilor:
Produsul coeficienților de interacțiune inter-populație este mai mic decât produsul coeficienților din interacțiunea populației.
Într-adevăr, să fie luate în considerare ratele naturale de creștere ale celor două speciiA 1 , A 2 sunt la fel. Atunci condiția necesară pentru stabilitate va fi
c 2 > b 12 ,c 1 >b 21 .
Aceste inegalități arată că o creștere a dimensiunii unui concurent suprimă propria creștere mai mult decât creșterea altui competitor. Dacă numărul ambelor specii este limitat, parțial sau complet, de resurse diferite, inegalitățile de mai sus sunt valabile. Dacă ambele specii au exact aceleași nevoi, atunci una dintre ele va fi mai viabilă și își va înlocui competitorul.
Comportamentul traiectoriilor de fază ale sistemului oferă o idee clară a posibilelor rezultate ale competiției. Să echivalăm laturile din dreapta ale ecuațiilor sistemului (9.2) cu zero:
X 1 (A 1-c 1 X 1 – b 12 X 2) = 0 (dx 1 /dt = 0),
X 2 (A 2 –b 21 X 1 – c 2 X 2) = 0 (dx 2 /dt = 0),
În acest caz, obținem ecuații pentru principalele izocline ale sistemului
X 2 = – b 21 X 1 / c 2 +A 2 /c 2, X 2 = 0
– ecuații ale izoclinelor tangentelor verticale.
X 2 = – c 1 X 1 / b 12 + A 1 /b 12 , X 1 = 0
– ecuații ale izoclinelor tangentelor verticale. Punctele de intersecție în perechi ale izoclinelor sistemelor tangente verticale și orizontale reprezintă soluții staționare ale sistemului de ecuații (9.2.) și coordonatele acestora ![]() sunt numere staţionare de specii concurente.
sunt numere staţionare de specii concurente.
Posibila locație a izoclinelor principale în sistemul (9.2) este prezentată în Fig. 9.1. Orez. 9.1Acorespunde supravieţuirii specieiX 1, fig. 9.1 b– supraviețuirea specieiX 2, fig. 9.1 V– coexistența speciilor când condiția (9.6) este îndeplinită. Figura 9.1Gdemonstrează sistemul de declanșare. Aici depinde rezultatul competiției condiții inițiale. Starea staționară diferită de zero (9.5) pentru ambele tipuri este instabilă. Aceasta este șaua prin care trece separatorul, separând zonele de supraviețuire ale fiecărei specii.

Orez. 9.1.Amplasarea principalelor izocline pe portretul de fază al sistemului Volterra de competiție de două tipuri (9.2) cu rapoarte diferite ale parametrilor. Explicații în text.
Pentru a studia competiția dintre specii, au fost efectuate experimente pe o mare varietate de organisme. De obicei, două specii strâns înrudite sunt selectate și crescute împreună și separat în condiții strict controlate. La anumite intervale se efectuează un recensământ complet sau selectiv al populaţiei. Datele din mai multe experimente replicate sunt înregistrate și analizate. Au fost efectuate cercetări asupra protozoarelor (în special, ciliate), multe specii de gândaci din genul Tribolium, drosophila și crustacee de apă dulce (daphnia). Multe experimente au fost efectuate pe populații microbiene (vezi prelegerea 11). Au fost efectuate experimente și în natură, inclusiv pe planari (Reynolds), două specii de furnici (Pontin), etc. În fig. 9.2. înfățișează curbele de creștere ale diatomeelor folosind aceeași resursă (ocupând aceeași nișă ecologică). Când este cultivat în monocultură Asterionella Formosa atinge un nivel constant de densitate și menține concentrația resursei (silicat) la un nivel constant scăzut. B. Când este cultivat în monocultură Synedrauina se comportă în mod similar și menține concentrația de silicați la un nivel și mai scăzut. B. În timpul cocultivării (în dublu exemplar) Synedrauina înlocuiește Asterionella formosa. Se pare că Synedra

Orez. 9.2.Concurență în diatomee. A - când este cultivat în monocultură Asterionella Formosa atinge un nivel constant de densitate și menține concentrația resursei (silicat) la un nivel constant scăzut. b - când este cultivat în monocultură Synedrauina se comportă în mod similar și menține concentrația de silicați la un nivel și mai scăzut. V - cu co-cultivare (în dublu exemplar) Synedruina înlocuiește Asterionella formosa. Se pare că Synedra câștigă competiția datorită capacității sale de a utiliza mai pe deplin substratul (vezi și Lectura 11).
Experimentele de studiere a concurenței de către G. Gause sunt larg cunoscute, demonstrând supraviețuirea uneia dintre speciile concurente și permițându-i să formuleze „legea excluderii competitive”. Legea prevede că într-o singură nișă ecologică poate exista o singură specie. În fig. 9.3. Rezultatele experimentelor lui Gause sunt prezentate pentru două specii de Parametium, care ocupă aceeași nișă ecologică (Fig. 9.3 a, b) și specii care ocupă nișe ecologice diferite (Fig. 9.3 c).

Orez. 9.3. A- Curbele de creștere a populației a două specii Parametiu la culturile cu o singură specie. cercuri negre - P Aurelia, cercuri albe – P. Caudatum
b- Curbele de creștere ale lui P Aurelia și P . Caudatum într-o cultură mixtă.
De Gause, 1934
Modelul de concurență (9.2) are dezavantaje, în special, rezultă că coexistența a două specii este posibilă numai dacă numărul acestora este limitat de factori diferiți, dar modelul nu indică cât de mari trebuie să fie diferențele pentru a asigura coexistența pe termen lung. . În același timp, se știe că pentru coexistența pe termen lung într-un mediu în schimbare este necesară o diferență care să atingă o anumită amploare. Introducerea elementelor stocastice în model (de exemplu, introducerea unei funcții de utilizare a resurselor) ne permite să investigăm cantitativ aceste probleme.
Sistem PREDATOR+VICTIM
 (9.7)
(9.7)
Aici, spre deosebire de (9.2), semnele b 12 Și b 21 sunt diferite. Ca și în cazul concurenței, originea
![]() (9.8)
(9.8)
este un punct special de tip nod instabil. Alte trei stări de echilibru posibile:
![]() ,(9.9)
,(9.9)
![]() (9.10)
(9.10)
![]() (9.11)
(9.11)
Astfel, este posibil ca doar prada să supraviețuiască (9.10), doar prădătorul (9.9) (dacă are alte surse de hrană) și coexistența ambelor specii (9.11). Am discutat deja ultima opțiune în Lectura 5. Tipuri posibile de portrete de fază pentru un sistem prădător-pradă sunt prezentate în Fig. 9.4.
Izoclinele tangentelor orizontale sunt drepte
X 2 = – b 21 X 1 /c 2 + A 1/c 2, X 2 = 0,
și izoclinele tangentelor verticale- Drept
X 2 = – c 1 X 1 /b 12 + A 2 /b 12 , X 1 = 0.
Punctele staționare se află la intersecția izoclinelor tangente verticale și orizontale.

Din fig. 9.4 este vizibil urmatorul. Sistem prădător-pradă (9.7) poate avea o poziţie stabilă de echilibru, în care o Populația de victime din rom s-a stins complet ( ) și au rămas doar prădători (perioada 2 din fig. 9.4 A). Evident, o astfel de situație poate fi realizată doar dacă, pe lângă tipul de victime în cauză, X 1 prădător X 2 – are surse suplimentare de alimentare. Acest fapt este reflectat în model de termenul pozitiv din partea dreaptă a ecuației pentru x2. Puncte speciale(1) și (3) (Fig. 9.4 A) sunt instabile. A doua posibilitate – o stare staționară stabilă în care populația de prădători s-a stins complet și rămâne doar prada – punct stabil(3) (Fig. 9.4 6 ). Există un punct special aici (1) – de asemenea un nod instabil.
În sfârșit, a treia posibilitate – coexistența durabilă a populațiilor de prădători și pradă (Fig. 9.4 V), ale căror numere staționare sunt exprimate prin formule (9.11).
Ca și în cazul unei singure populații (vezi Lectura 3), pentru model (9.7) Este posibil să se dezvolte un model stocastic, dar nu poate fi rezolvat în mod explicit. Prin urmare, ne vom limita la considerații generale. Să presupunem, de exemplu, că punctul de echilibru este situat la o anumită distanță de fiecare dintre axe. Apoi pentru traiectorii de fază pe care valorileX 1 , X 2 rămâne suficient de mare, un model determinist va fi destul de satisfăcător. Dar dacă la un moment dat în traiectoria fazei orice variabilă nu este foarte mare, atunci fluctuațiile aleatorii pot deveni semnificative. Ele duc la faptul că punctul reprezentativ se deplasează pe una dintre axe, ceea ce înseamnă dispariția speciilor corespunzătoare.
Astfel, modelul stocastic se dovedește a fi instabil, deoarece „deriva” stocastică duce mai devreme sau mai târziu la dispariția uneia dintre specii. În acest tip de model, prădătorul dispare în cele din urmă, fie din întâmplare, fie pentru că populația sa de pradă este eliminată prima. Modelul stocastic al sistemului prădător-pradă explică bine experimentele lui Gause (Gause, 1934), in care ciliati Paramettum candatum a servit drept victimă pentru un alt ciliat Didinium nasatum – prădător. Așteptată conform ecuațiilor deterministe (9.7) Numerele de echilibru în aceste experimente au fost de aproximativ cinci indivizi din fiecare specie, așa că nu este surprinzător că în fiecare experiment repetat fie prădătorii, fie prada (și după ei prădătorii) au murit destul de repede. Rezultatele experimentelor sunt prezentate în fig. 9.5.

Orez. 9.5. Înălţime Parametium caudatum și ciliați prădători Dadinium nasutum. Din : Gause G.F. Lupta pentru existență. Baltimore, 1934
Deci, o analiză a modelelor Volterra de interacțiune între specii arată că, în ciuda varietății mari de tipuri de comportament ale unor astfel de sisteme, nu pot exista deloc fluctuații neatenuate ale numărului în modelul speciilor concurente. Cu toate acestea, astfel de oscilații sunt observate în natură și în experiment. Necesitatea explicației lor teoretice a fost unul dintre motivele formulării descrierilor modelelor într-o formă mai generală.
Modele generalizate de interacțiune de două tipuri
S-a sugerat număr mare modele care descriu interacțiunea speciilor, ale căror părți din dreapta ecuațiilor au fost funcții ale numărului de populații care interacționează. A fost abordată problema dezvoltării criteriilor generale pentru a stabili ce tip de funcții pot descrie comportamentul mărimii temporare a populației, inclusiv fluctuațiile stabile. Cele mai faimoase dintre aceste modele aparțin lui Kolmogorov (1935, articol revizuit - 1972) și Rosenzweig (1963).
 (9.12)
(9.12)
Modelul include următoarele ipoteze:
1) Prădătorii nu interacționează între ei, adică rata de reproducere a prădătorilor k 2 și numărul victimelor L exterminat pe unitatea de timp de către un prădător nu depinde de y.
2) Creșterea numărului de pradă în prezența prădătorilor este egală cu creșterea în absența prădătorilor minus numărul de pradă exterminat de către prădători. Funcții k 1 (X), k 2 (X), L(X), sunt continue și definite pe semiaxa pozitivă X, y³ 0.
3) dk 1 /dx< 0. Aceasta înseamnă că rata de reproducere a prăzii în absența unui prădător scade monoton odată cu creșterea numărului de pradă, ceea ce reflectă disponibilitatea limitată a hranei și a altor resurse.
4) dk 2 /dx> 0, k 2 (0) < 0 < k 2 (¥ ). Odată cu creșterea numărului de pradă, coeficientul de reproducere al prădătorilor scade monoton odată cu creșterea numărului de pradă, trecând de la valori negative, (când nu e nimic de mâncat) la pozitiv.
5) Numărul de pradă distrusă de un prădător pe unitatea de timp L(X)> 0 la N> 0; L(0)=0.
Tipurile posibile de portrete de fază ale sistemului (9.12) sunt prezentate în Fig. 9.6:

Orez. 9.6.Portrete de fază ale sistemului Kolmogorov (9.12), care descrie interacțiunea a două tipuri la rapoarte diferite parametrii. Explicații în text.
Soluțiile staționare (sunt două sau trei) au următoarele coordonate:
(1). ` x=0;` y=0.
Originea coordonatelor pentru orice valoare a parametrilor este o șa (Fig. 9.6 a-d).
(2). ` x=A,` y=0.(9.13)
Adeterminată din ecuația:
k 1 (A)=0.
Staționar soluția (9.13) este o șa dacă B< A (Fig. 9.6 A, b, G), B determinată din ecuație
k 2 (B)=0
Punctul (9.13) este plasat în cadranul pozitiv dacă B>A . Acesta este un nod stabil .
Ultimul caz, care corespunde morții prădătorului și supraviețuirii prăzii, este prezentat în Fig. 9.6 V.
(3). ` x=B,` y=C.(9.14)
Valoarea lui C se determină din ecuațiile:
Punctul (9.14) – focalizare (Fig.9.6 A) sau nod (Fig.9.6 G), a cărui stabilitate depinde de semnul cantitățiis
s 2 = – k 1 (B) – k 1 (B)B+L(B)C.
Dacă s>0, un punct este stabil dacăs<0 ‑ точка неустойчива, и вокруг нее могут существовать предельные циклы (рис. 9.6 b)
În literatura străină, un model similar propus de Rosenzweig și MacArthur (1963) este mai des luat în considerare:
 (9.15)
(9.15)
Unde f(X) - rata de modificare a numărului de victime Xîn absența prădătorilor, F( X y) - intensitatea prădării, k- coeficient care caracterizează eficiența procesării biomasei de pradă în biomasă de prădători; e- mortalitatea prădătorilor.
Modelul (9.15) se reduce la un caz special al modelului Kolmogorov (9.12) sub următoarele ipoteze:
1) numărul de prădători este limitat doar de numărul de pradă,
2) viteza cu care un anumit prădător mănâncă prada depinde numai de densitatea populației de pradă și nu depinde de densitatea populației de prădători.
Atunci ecuațiile (9.15) iau forma.

Când se descrie interacțiunea speciilor reale, părțile din dreapta ale ecuațiilor sunt specificate în conformitate cu ideile despre realitățile biologice. Să luăm în considerare unul dintre cele mai populare modele de acest tip.
Model de interacțiune între două tipuri de insecte (MacArthur, 1971)
Modelul, pe care îl vom analiza mai jos, a fost folosit pentru a rezolva problema practică a controlului insectelor dăunătoare prin sterilizarea masculilor uneia dintre specii. Pe baza caracteristicilor biologice ale interacțiunii dintre specii, a fost scris următorul model
 (9.16)
(9.16)
Aici X y- biomasa a doua tipuri de insecte. Interacțiunile trofice ale speciilor descrise în acest model sunt foarte complexe. Aceasta determină forma polinoamelor din partea dreaptă a ecuațiilor.
Să ne uităm la partea dreaptă a primei ecuații. Specii de insecte X mănâncă larvele speciei la(membru +k 3 y), dar adulţii din specie la mănâncă larvele speciei X supuse abundenței mari de specii X sau la sau ambele tipuri (membri – k 4 xy, – y 2). La mic X mortalitatea speciilor X mai mare decât creșterea sa naturală (1 – k 1 +k 2 x–x 2 < 0 la mic X).În a doua ecuație termenul k 5 reflectă creșterea naturală a speciei y; – k 6 y – autocontrol de acest tip,– k 7 X– consumul de larve ale speciei la specii de insecte x, k 8 X y – creșterea biomasei speciilor la datorită consumului de către insectele adulte ale speciei la larvele speciei X.
În fig. 9.7 este prezentat un ciclu limită, care este traiectoria unei soluții periodice stabile a sistemului (9.16).

Soluția la întrebarea cum să se asigure coexistența unei populații cu mediul ei biologic, desigur, nu poate fi obținută fără a ține cont de specificul unui anumit sistem biologic și de o analiză a tuturor interrelațiilor sale. În același timp, studiul modelelor matematice formale ne permite să răspundem la câteva întrebări generale. Se poate susține că pentru modele precum (9.12), faptul compatibilității sau incompatibilității populațiilor nu depinde de mărimea lor inițială, ci este determinat doar de natura interacțiunii speciilor. Modelul ajută la răspunsul la întrebarea: cum să influențezi biocenoza și să o gestionezi pentru a distruge rapid speciile dăunătoare.
Managementul poate fi redus la o schimbare bruscă, pe termen scurt, a valorilor populației XȘi u. Această metodă corespunde unor metode de control, cum ar fi distrugerea unică a uneia sau ambelor populații prin mijloace chimice. Din afirmația formulată mai sus reiese clar că pentru populațiile compatibile această metodă de control va fi ineficientă, deoarece în timp sistemul va ajunge din nou la un regim staționar.
O altă modalitate este de a schimba tipul de funcții de interacțiune între vizualizări, de exemplu, atunci când se schimbă valorile parametrilor sistemului. Metodele de control biologic îi corespund acestei metode parametrice. Astfel, la introducerea masculilor sterilizati, coeficientul scade crestere naturala populatiilor. Dacă în același timp obținem un alt tip de portret de fază, unul în care există doar o stare staționară stabilă cu numere zero dăunători, controlul va duce la rezultatul dorit. – distrugerea populaţiei unei specii dăunătoare. Este interesant de menționat că uneori este recomandabil să aplicați impactul nu asupra dăunătorului în sine, ci asupra partenerului său. În general, este imposibil de spus care metodă este mai eficientă. Aceasta depinde de controalele disponibile și de forma explicită a funcțiilor care descriu interacțiunea populațiilor.
Model de A.D. Bazykin
Analiza teoretică a modelelor de interacțiuni dintre specii a fost realizată cel mai cuprinzător în cartea lui A.D. Bazykin „Biofizica populațiilor care interacționează” (M., Nauka, 1985).
Să luăm în considerare unul dintre modelele prădător-pradă studiate în această carte.
 (9.17)
(9.17)
Sistemul (9.17) este o generalizare a celui mai simplu model Volterra prădător-pradă (5.17) ținând cont de efectul saturației prădătorilor. Modelul (5.17) presupune că intensitatea pășunatului de pradă crește liniar odată cu creșterea densității de pradă, ceea ce nu corespunde realității la densități mari de pradă. Pot fi alese diferite funcții pentru a descrie dependența dietei unui prădător de densitatea prăzii. Cel mai important este ca funcția aleasă cu creștere X tinde asimptotic la o valoare constantă. Modelul (9.6) a folosit o dependență logistică. În modelul lui Bazykin, hiperbola este aleasă ca atare funcție X/(1+px). Să ne amintim că aceasta este forma formulei Monod, care descrie dependența ratei de creștere a microorganismelor de concentrația substratului. Aici prada joacă rolul de substrat, iar prădătorul joacă rolul de microorganisme. .
Sistemul (9.17) depinde de șapte parametri. Numărul de parametri poate fi redus prin înlocuirea variabilelor:
X® (ANUNȚ)X; y ® (ANUNȚ)/y;
t® (1/A)t; g (9,18)
și depinde de patru parametri.
Pentru un studiu calitativ complet, este necesar să se împartă spațiul parametrilor cu patru dimensiuni în zone cu diferite tipuri de comportament dinamic, i.e. construi un portret parametric sau structural al sistemului.
Apoi este necesar să se construiască portrete de fază pentru fiecare dintre zonele portretului parametric și să se descrie bifurcațiile care apar cu portretele de fază la granițele diferitelor zone ale portretului parametric.
Construcția unui portret parametric complet se realizează sub forma unui set de „slice” (proiecții) unui portret parametric de dimensiuni reduse cu valori fixe ale unora dintre parametri.
Portret parametric al sistemului (9.18) pentru fix g si mici e prezentate în Fig. 9.8. Portretul conține 10 zone cu diferite tipuri de comportament ale traiectoriilor de fază.

Orez. 9.8.Portret parametric al sistemului (9.18) pentru fixg
si mici e
Comportamentul sistemului la diferite rapoarte ale parametrilor poate fi semnificativ diferit (Fig. 9.9). Sistemul permite:
1) un echilibru stabil (regiunile 1 și 5);
2) un ciclu limită stabil (regiunile 3 și 8);
3) două echilibre stabile (regiunea 2)
4) ciclu limită stabil și echilibru instabil în interiorul acestuia (regiunile 6, 7, 9, 10)
5) ciclu limită stabil și echilibru stabil în afara acestuia (regiunea 4).
În regiunile parametrice 7, 9, 10, regiunea de atracție a echilibrului este limitată de un ciclu limită instabil aflat în interiorul unuia stabil. Cea mai interesantă structură este portretul de fază, corespunzător zonei 6 din portretul parametric. Este prezentată în detaliu în Fig. 9.10.

Zona de atracție a echilibrului B 2 (umbrită) este un „melc” care se răsucește din focarul instabil B 1. Dacă se știe că în momentul inițial de timp sistemul se afla în vecinătatea lui B 1, atunci este posibil să se judece dacă traiectoria corespunzătoare va atinge echilibrul B 2 sau un ciclu limită stabil care înconjoară trei puncte de echilibru C (șa), B 1 și B 2 pe baza considerațiilor probabilistice.

Fig.9.10.Portret de fază al sistemului 9.18 pentru regiunea parametrică 6. Regiunea de atracție B 2 este umbrită
Într-un portret parametric(9.7) sunt 22 diverse limite de bifurcație care se formează 7 diferite tipuri de bifurcații. Studiul lor ne permite să identificăm tipuri posibile de comportament al sistemului atunci când parametrii acestuia se modifică. De exemplu, la mutarea din zonă 1 la zona 3 are loc nașterea unui ciclu limită mic sau nașterea blândă a auto-oscilațiilor în jurul unui singur echilibru ÎN. O naștere moale similară a auto-oscilațiilor, dar în jurul unuia dintre echilibre și anume B 1 , apare la trecerea granițelor regiunilor 2 și 4. La părăsirea zonei 4 la zona 5 ciclu limită stabil în jurul unui punctB 1 „explosează” pe bucla separatricelor și singurul punct de atragere rămâne echilibrul B 2 etc.
Un interes deosebit pentru practică este, desigur, dezvoltarea criteriilor pentru apropierea unui sistem de granițele de bifurcație. Într-adevăr, biologii sunt foarte conștienți de proprietatea de „tampon” sau „flexibilitate” a sistemelor ecologice naturale. Acești termeni se referă de obicei la capacitatea unui sistem de a absorbi influențele externe. Atâta timp cât intensitatea influenței externe nu depășește o anumită valoare critică, comportamentul sistemului nu suferă modificări calitative. Pe planul de fază, aceasta corespunde revenirii sistemului la o stare stabilă de echilibru sau la un ciclu limită stabil, ai cărui parametri nu diferă mult de cel inițial. Când intensitatea impactului depășește nivelul permis, sistemul „se defectează” și intră într-un mod calitativ diferit de comportament dinamic, de exemplu, pur și simplu se stinge. Acest fenomen corespunde unei tranziții de bifurcație.
Fiecare tip de tranziție de bifurcație are propriile sale caracteristici distinctive, care fac posibilă aprecierea pericolului unei astfel de tranziții pentru ecosistem. Iată câteva criterii generale care indică apropierea unei granițe periculoase. Ca și în cazul unei specii, dacă, atunci când numărul uneia dintre specii scade, sistemul „se blochează” în apropierea unui punct instabil de șa, care se exprimă într-o restabilire foarte lentă a numărului la valoarea inițială, atunci sistemul este aproape de limita critică. Un indicator al pericolului este, de asemenea, o schimbare a formei fluctuațiilor numărului de prădători și pradă. Dacă oscilațiile apropiate de armonice devin de relaxare, iar amplitudinea oscilațiilor crește, aceasta poate duce la o pierdere a stabilității sistemului și la dispariția uneia dintre specii.
Aprofundarea în continuare a teoriei matematice a interacțiunii dintre specii merge pe linia detalierii structurii populațiilor înseși și luării în considerare a factorilor temporali și spațiali.
Literatură.
Kolmogorov A.N. Studiu calitativ al modelelor matematice ale dinamicii populației. // Probleme de cibernetică. M., 1972, numărul 5.
MacArtur R. Analiza grafică a sistemelor ecologice // Raportul Diviziei de biologie Universitatea Perinceton. 1971
A.D. Bazykin „Biofizica populațiilor care interacționează”. M., Nauka, 1985.
V. Volterra: „Teoria matematică a luptei pentru existență”. M.. Știință, 1976
Gause G.F. Lupta pentru existență. Baltimore, 1934.
Dinamica populației este una dintre ramurile modelării matematice. Este interesant pentru că are aplicații specifice în biologie, ecologie, demografie și economie. Există mai multe modele de bază în această secțiune, dintre care unul, modelul Predator-Prey, este discutat în acest articol.
Primul exemplu de model în ecologia matematică a fost modelul propus de V. Volterra. El a fost primul care a considerat modelul relației dintre prădător și pradă.
Să luăm în considerare afirmația problemei. Să fie două tipuri de animale, dintre care unul îl devorează pe celălalt (prădători și pradă). În acest caz, se fac următoarele ipoteze: resursele alimentare ale prăzii nu sunt limitate și, prin urmare, în absența unui prădător, populația de pradă crește după o lege exponențială, în timp ce prădătorii, separați de victimele lor, mor treptat. de foame, tot după o lege exponenţială. Odată ce prădătorii și prada încep să trăiască în imediata apropiere unul de celălalt, schimbările în dimensiunea populației lor devin interdependente. În acest caz, evident, creșterea relativă a numărului de pradă va depinde de mărimea populației de prădători și invers.
În acest model, se presupune că toți prădătorii (și toate prada) sunt în aceleași condiții. În același timp, resursele alimentare ale victimelor sunt nelimitate, iar prădătorii se hrănesc exclusiv cu victime. Ambele populații trăiesc într-o zonă limitată și nu interacționează cu alte populații și nu există alți factori care ar putea afecta dimensiunea populației.
Modelul matematic „prădător-pradă” în sine constă dintr-o pereche de ecuații diferențiale care descriu dinamica populațiilor de prădători și pradă în cel mai simplu caz, când există o populație de prădători și una de pradă. Modelul este caracterizat de fluctuații ale mărimii ambelor populații, cu vârful la prădători ușor în spatele vârfului la pradă. Acest model poate fi găsit în multe lucrări despre dinamica populației sau modelare matematică. Acesta a fost acoperit și analizat pe scară largă folosind metode matematice. Cu toate acestea, formulele pot să nu ofere întotdeauna o idee evidentă a procesului care are loc.
Este interesant să aflăm exact cum dinamica populației din acest model depinde de parametrii inițiali și cât de mult corespunde realității și bunului simț și să vedem acest lucru grafic fără a recurge la calcule complexe. În acest scop, pe baza modelului Volterra, a fost creat un program în mediul Mathcad14.
Mai întâi, să verificăm modelul pentru conformitatea cu condițiile reale. Pentru a face acest lucru, să luăm în considerare cazurile degenerate când doar una dintre populații trăiește în condiții date. Teoretic, s-a demonstrat că, în absența prădătorilor, populația de pradă crește nelimitat în timp, iar populația de prădători în absența prăzii se stinge, ceea ce corespunde în general modelului și situației reale (cu formularea specificată a problemă).
Rezultatele obținute le reflectă pe cele teoretice: prădătorii se sting treptat (Fig. 1), iar numărul de pradă crește la nesfârșit (Fig. 2).
Fig. 1 Dependența numărului de prădători de timp în absența prăzii

Fig. 2 Dependența numărului de pradă în timp în absența prădătorilor
După cum se poate observa, în aceste cazuri sistemul corespunde modelului matematic.
Să luăm în considerare modul în care sistemul se comportă în funcție de diferiți parametri inițiali. Să fie două populații - lei și antilope - prădători și, respectiv, pradă, și se dau indicatorii inițiali. Apoi obținem următoarele rezultate (Fig. 3):
Tabelul 1. Coeficienții modului oscilator al sistemului

Fig.3 Sistem cu valorile parametrilor din tabelul 1
Să analizăm datele obținute pe baza graficelor. Odată cu creșterea inițială a populației de antilope, se observă o creștere a numărului de prădători. Rețineți că creșterea maximă a populației de prădători se observă mai târziu, în timpul scăderii populației de pradă, ceea ce este destul de în concordanță cu conceptele reale și cu modelul matematic. Într-adevăr, o creștere a numărului de antilope înseamnă o creștere a resurselor de hrană pentru lei, ceea ce presupune o creștere a numărului acestora. În plus, consumul activ de antilope de către lei duce la o scădere rapidă a numărului de pradă, ceea ce nu este surprinzător, având în vedere apetitul prădătorului, sau mai degrabă frecvența prădătorilor care mănâncă pradă. O scădere treptată a numărului de prădători duce la o situație în care populația de pradă se află în condiții favorabile creșterii. Apoi situația se repetă cu o anumită perioadă. Concluzionăm că aceste condiții nu sunt potrivite pentru dezvoltarea armonioasă a indivizilor, deoarece implică scăderi accentuate ale populației de pradă și creșteri puternice la ambele populații.
Să setăm acum numărul inițial al prădătorului egal cu 200 de indivizi menținând în același timp alți parametri (Fig. 4).
Tabelul 2. Coeficienții modului oscilator al sistemului

Fig.4 Sistem cu valorile parametrilor din Tabelul 2
Acum sistemul oscilează mai natural. În aceste ipoteze, sistemul există destul de armonios, nu există creșteri și scăderi puternice ale numărului de numere în ambele populații. Concluzionăm că, cu acești parametri, ambele populații se dezvoltă suficient de uniform pentru a trăi împreună pe același teritoriu.
Să setăm numărul inițial de prădători la 100 de indivizi, numărul de pradă la 200, păstrând în același timp alți parametri (Fig. 5).
Tabelul 3. Coeficienții modului oscilator al sistemului

Fig.5 Sistem cu valorile parametrilor din Tabelul 3
În acest caz, situația este apropiată de prima situație luată în considerare. Rețineți că, odată cu creșterea reciprocă a populațiilor, trecerile de la o creștere la o scădere a populației de pradă au devenit mai lin, iar populația de prădători rămâne în absența prăzii la o valoare numerică mai mare. Concluzionăm că atunci când o populație este strâns legată de alta, interacțiunea lor are loc mai armonios dacă populațiile inițiale specifice sunt suficient de mari.
Să luăm în considerare modificarea altor parametri de sistem. Fie numerele inițiale să corespundă celui de-al doilea caz. Să creștem rata de reproducere a victimelor (Fig. 6).
Tabelul 4. Coeficienții modului oscilator al sistemului

Fig.6 Sistem cu valorile parametrilor din Tabelul 4
Să comparăm acest rezultat cu rezultatul obținut în al doilea caz. În acest caz, se observă o creștere mai rapidă a victimei. În acest caz, atât prădătorul, cât și prada se comportă ca în primul caz, ceea ce s-a explicat prin dimensiunea redusă a populației. Cu această interacțiune, ambele populații ajung la valori mult mai mari decât în al doilea caz.
Acum să creștem rata de creștere a prădătorilor (Fig. 7).
Tabelul 5. Coeficienții modului oscilator al sistemului

Fig.7 Sistem cu valorile parametrilor din Tabelul 5
Să comparăm rezultatele în mod similar. În acest caz, caracteristicile generale ale sistemului rămân aceleași, cu excepția modificării perioadei. După cum era de așteptat, perioada a devenit mai scurtă, ceea ce se explică prin scăderea rapidă a populației de prădători în absența prăzii.
Și, în sfârșit, să schimbăm coeficientul de interacțiune interspecifică. În primul rând, să creștem frecvența prădătorilor care mănâncă pradă:
Tabelul 6. Coeficienții modului oscilator al sistemului

Fig.8 Sistem cu valorile parametrilor din Tabelul 6
Deoarece prădătorul își mănâncă prada mai des, dimensiunea maximă a populației a crescut față de al doilea caz, iar diferența dintre dimensiunile maxime și minime ale populației a scăzut și ea. Perioada de oscilație a sistemului rămâne aceeași.
Și acum să reducem frecvența prădătorilor care mănâncă pradă:
Tabelul 7. Coeficienții modului oscilator al sistemului

Fig.9 Sistem cu valorile parametrilor din Tabelul 7
Acum prădătorul mănâncă prada mai rar, dimensiunea maximă a populației a scăzut față de cel de-al doilea caz, iar dimensiunea maximă a populației de pradă a crescut de 10 ori. Rezultă că, în aceste condiții, populația de pradă are o mai mare libertate în ceea ce privește reproducerea, deoarece prădătorul are nevoie de mai puțină masă pentru a obține suficientă. Diferența dintre dimensiunile maxime și minime ale populației a scăzut și ea.
Când se încearcă modelarea proceselor complexe din natură sau societate, într-un fel sau altul, se pune întrebarea cu privire la corectitudinea modelului. Desigur, la modelare, procesul este simplificat și unele detalii minore sunt neglijate. Pe de altă parte, există pericolul de a simplifica prea mult modelul, eliminând astfel trăsăturile importante ale fenomenului alături de cele neimportante. Pentru a evita această situație, înainte de modelare este necesar să se studieze domeniul în care este utilizat acest model, să se examineze toate caracteristicile și parametrii acestuia și, cel mai important, să se evidențieze acele caracteristici care sunt cele mai semnificative. Procesul trebuie să aibă o descriere naturală, intuitivă de înțeles, coincizând în punctele principale cu modelul teoretic.
Modelul luat în considerare în această lucrare are o serie de dezavantaje semnificative. De exemplu, asumarea unor resurse nelimitate pentru victimă, absența unor factori terți care influențează mortalitatea ambelor specii etc. Toate aceste ipoteze nu reflectă situația reală. Cu toate acestea, în ciuda tuturor neajunsurilor, modelul a devenit larg răspândit în multe domenii, chiar departe de ecologie. Acest lucru poate fi explicat prin faptul că sistemul „prădător-pradă” oferă o idee generală despre interacțiunea speciilor. Interacțiunile cu mediul și alți factori pot fi descrise prin alte modele și analizate împreună.
Relațiile prădător-pradă sunt o caracteristică esențială tipuri variate activități de viață în care există o coliziune între două părți care interacționează. Acest model are loc nu numai în ecologie, ci și în economie, politică și alte domenii de activitate. De exemplu, una dintre domeniile legate de economie este analiza pieței muncii, luând în considerare potențialii lucrători disponibili și locurile de muncă vacante. Acest subiect ar fi o continuare interesantă a lucrărilor asupra modelului prădător-pradă.
Predare- o formă de relații trofice între organisme de diferite specii, în care unul dintre ele ( prădător) atacă pe altul ( victimă) și se hrănește cu carnea sa, adică există de obicei un act de ucidere a victimei.
Sistem prădător-pradă- un ecosistem complex pentru care se realizează relații pe termen lung între speciile de prădători și prada, un exemplu tipic de coevoluție.
Coevoluția este evoluția comună a speciilor biologice care interacționează într-un ecosistem.
Relația dintre prădători și prada lor se dezvoltă ciclic, ilustrând un echilibru neutru.
1. Singurul factor limitator care limitează reproducerea prăzilor este presiunea asupra acestora din partea prădătorilor. Resursele limitate ale mediului pentru victimă nu sunt luate în considerare.
2. Reproducerea prădătorilor este limitată de cantitatea de hrană pe care o obțin (numărul de victime).
În esență, modelul Lotka-Volterra este o descriere matematică a principiului darwinian al luptei pentru existență.
Sistemul Volterra-Lotka, numit adesea sistemul prădător-pradă, descrie interacțiunea a două populații - prădători (de exemplu, vulpi) și pradă (de exemplu, iepuri de câmp), care trăiesc conform „legilor” ușor diferite. Prada își menține populația consumând o resursă naturală, cum ar fi iarba, ceea ce face ca populația să crească exponențial dacă nu există prădători. Prădătorii își mențin populația doar „mâncându-și” victimele. Prin urmare, dacă populația de pradă dispare, atunci populația de prădători scade exponențial. Mâncarea de pradă de către prădători dăunează populației de pradă, dar în același timp oferă o resursă suplimentară pentru reproducerea prădătorilor.
Întrebare
PRINCIPIUL DIMENSIUNII MINIMĂ A POPULAȚIEI
un fenomen care există în mod natural în natură, caracterizat ca un principiu natural unic, adică fiecare specie de animal are o anumită dimensiune minimă a populației, a cărei încălcare amenință existența populației și, uneori, a speciei în ansamblu.
regula maximă a populației, constă în faptul că populația nu poate crește la infinit, din cauza epuizării resurselor alimentare și a condițiilor de reproducere (teoria Andrevarta-Birch) și a limitării impactului unui complex de factori de mediu abiotici și biotici (teoria Fredericks).
Întrebare
Deci, așa cum era deja clar pentru Fibonacci, creșterea populației este proporțională cu dimensiunea sa și, prin urmare, dacă creșterea populației nu este limitată de niciun factor extern, ea accelerează continuu. Să descriem această creștere matematic.
Creșterea populației este proporțională cu numărul de indivizi din ea, adică Δ N~N, Unde N- dimensiunea populației și Δ N- modificarea acesteia într-o anumită perioadă de timp. Dacă această perioadă este infinitezimală, putem scrie asta dN/dt=r × N , Unde dN/dt- modificarea dimensiunii populației (creștere) și r - potenţialul de reproducere, o variabilă care caracterizează capacitatea unei populații de a-și crește dimensiunea. Ecuația dată este numită model exponenţial creşterea populaţiei (Fig. 4.4.1).
Fig.4.4.1. Crestere exponentiala.
După cum este ușor de înțeles, pe măsură ce timpul crește, populația crește din ce în ce mai repede și destul de curând se grăbește la infinit. Desigur, niciun habitat nu poate susține existența unei populații cu un număr infinit. Cu toate acestea, există o serie de procese de creștere a populației care, pe o anumită perioadă de timp, pot fi descrise folosind un model exponențial. Vorbim de cazuri de creștere nelimitată, când o anumită populație populează un mediu cu un exces de resurse libere: vacile și caii populează pampa, gândacii de făină populează un lift de cereale, drojdia populează o sticlă de suc de struguri etc.
În mod firesc, creșterea exponențială a populației nu poate dura pentru totdeauna. Mai devreme sau mai târziu resursa va fi epuizată, iar creșterea populației va încetini. Cum va fi această frânare? Ecologia practică cunoaște o varietate de opțiuni: o creștere bruscă a numărului, urmată de dispariția unei populații care și-a epuizat resursele și o încetinire treptată a creșterii pe măsură ce se apropie de un anumit nivel. Cel mai simplu mod de a-l descrie este frânarea lentă. Cel mai simplu model care descrie o astfel de dinamică se numește logisticăși a fost propus (pentru a descrie creșterea populației umane) de către matematicianul francez Verhulst încă din 1845. În 1925, un model similar a fost redescoperit de ecologistul american R. Pearl, care a sugerat că este universal.
În modelul logistic este introdusă o variabilă K- capacitate medie, dimensiunea populației de echilibru la care consumă toate resursele disponibile. Creșterea modelului logistic este descrisă de ecuație dN/dt=r × N × (K-N)/K (Fig. 4.4.2).

Orez. 4.4.2. Creșterea logisticii
Pa N este mică, creșterea populației este influențată în principal de factor r× N iar creșterea populației se accelerează. Când devine suficient de mare, dimensiunea populației începe să fie influențată în principal de factor (K-N)/K iar creșterea populației începe să încetinească. Când N=K, (K-N)/K=0 iar creșterea populației se oprește.
Cu toată simplitatea ei, ecuația logistică descrie în mod satisfăcător multe cazuri observate în natură și este încă folosită cu succes în ecologia matematică.
Nr. 16. Strategia de supraviețuire ecologică- un set dezvoltat evolutiv de proprietăți ale unei populații care vizează creșterea probabilității de supraviețuire și de a lăsa urmași.
Deci A.G. Ramensky (1938) a distins trei tipuri principale de strategii de supraviețuire în rândul plantelor: violenți, pacienți și explerenți.
Violente (siloviki) - suprimă toți concurenții, de exemplu, copacii care formează păduri indigene.
Pacienții sunt specii care pot supraviețui în condiții nefavorabile („iubitoare de umbră”, „iubitoare de sare”, etc.).
Explerenții (fillers) sunt specii care pot apărea rapid acolo unde comunitățile indigene sunt deranjate - în poieni și zone arse (aspen), în adâncime etc.
Strategiile ecologice ale populațiilor sunt foarte diverse. Dar, în același timp, toată diversitatea lor se află între două tipuri de selecție evolutivă, care sunt notate de constantele ecuației logistice: r-strategy și K-strategy.
| Semn | r-strategii | K-strategii |
| Mortalitate | Nu depinde de densitate | Depinde de densitate |
| Competiție | Slab | Acut |
| Durată de viaţă | Mic de statura | Lung |
| Viteza de dezvoltare | Rapid | Încet |
| Timp de reproducere | Din timp | Târziu |
| Îmbunătățirea reproducerii | Slab | Mare |
| Tipul curbei de supraviețuire | Concav | Convex |
| Marimea corpului | Mic | Mare |
| Caracterul urmașilor | Multe, mici | Mic mare |
| Dimensiunea populației | Fluctuații puternice | Constant |
| Mediu preferat | Schimbabil | Constant |
| Etapele succesiunii | Din timp | Târziu |
Informații conexe.
Agenția Federală pentru Educație
Instituție de învățământ de stat
studii profesionale superioare
„Universitatea Tehnică de Stat Izhevsk”
Facultatea de Matematică Aplicată
Departamentul „Modelarea matematică a proceselor și tehnologiilor”
Lucru de curs
la disciplina „Ecuații diferențiale”
Subiect: „Cercetarea calitativă a modelului prădător-pradă”
Izhevsk 2010
INTRODUCERE
1. PARAMETRI ȘI ECUAȚIA DE BAZĂ ALE MODELULUI „PRĂDATOR-VICTICĂ”.
2.2 Modele Voltaire generalizate de tip „prădător-pradă”.
3. APLICAREA PRACTICĂ A MODELULUI „PRĂDATOR-VICTICĂ”.
CONCLUZIE
BIBLIOGRAFIE
INTRODUCERE
În prezent, problemele de mediu sunt de o importanță capitală. Un pas important în rezolvarea acestor probleme este dezvoltarea modelelor matematice ale sistemelor ecologice.
Una dintre principalele sarcini ale ecologiei în stadiul actual este studiul structurii și funcționării sistemelor naturale, căutarea modelelor generale. Matematica a avut o mare influență asupra ecologiei, contribuind la formarea ecologiei matematice, în special secțiuni precum teoria ecuațiilor diferențiale, teoria stabilității și teoria controlului optim.
Una dintre primele lucrări în domeniul ecologiei matematice a fost opera lui A.D. Lotki (1880 - 1949), care a fost primul care a descris interacțiunea diferitelor populații legate prin relații prădător-pradă. O mare contribuție la studiul modelului prădător-pradă a avut-o V. Volterra (1860 - 1940), V.A. Kostitsyn (1883-1963) În prezent, ecuațiile care descriu interacțiunea populațiilor sunt numite ecuații Lotka-Volterra.
Ecuațiile Lotka-Volterra descriu dinamica valorilor medii - dimensiunea populației. În prezent, pe baza acestora, au fost construite modele mai generale de interacțiune a populației, descrise prin ecuații integro-diferențiale, și sunt studiate modele controlate prădător-pradă.
Una dintre problemele importante ale ecologiei matematice este problema stabilității ecosistemelor și a managementului acestor sisteme. Managementul poate fi efectuat cu scopul de a transfera un sistem dintr-o stare stabilă în alta, în scopul utilizării sau refacerii acestuia.
1. PARAMETRII ȘI ECUAȚIA DE BAZĂ ALE MODELULUI PREDATOR-PRIMATE
Încercările de a modela matematic dinamica atât a populațiilor biologice individuale, cât și a comunităților, inclusiv a populațiilor care interacționează ale diferitelor specii, au fost făcute de mult timp. Unul dintre primele modele de creștere a populației izolate (2.1) a fost propus în 1798 de Thomas Malthus:
Acest model este specificat de următorii parametri:
N - dimensiunea populației;
Diferența dintre ratele natalității și cele ale mortalității.
Integrând această ecuație obținem:
![]() , (1.2)
, (1.2)
unde N(0) este mărimea populației la momentul t = 0. Evident, modelul Malthus la > 0 dă o creștere infinită a numărului, ceea ce nu se observă niciodată la populațiile naturale, unde resursele care asigură această creștere sunt întotdeauna limitate. Modificări ale numărului de populații de floră și faună nu pot fi descrise lege simplă Malthus, dinamica creșterii este influențată de multe motive interdependente - în special, reproducerea fiecărei specii este autoreglată și modificată, astfel încât această specie să fie păstrată în procesul de evoluție.
Descrierea matematică a acestor modele este tratată de ecologia matematică - știința relațiilor dintre organismele vegetale și animale și comunitățile pe care le formează între ele și cu mediul.
Cel mai serios studiu al modelelor de comunități biologice, inclusiv mai multe populații de specii diferite, a fost efectuat de matematicianul italian Vito Volterra:
 ,
,
unde este dimensiunea populației;
Ratele de creștere naturală (sau mortalitate) a unei populații; - coeficienţii de interacţiune interspecifică. În funcție de alegerea coeficienților, modelul descrie fie lupta speciilor pentru o resursă comună, fie o interacțiune prădător-pradă, atunci când o specie este hrană pentru alta. Dacă lucrările altor autori s-au concentrat pe construcția diferitelor modele, atunci V. Volterra a efectuat un studiu aprofundat al modelelor construite ale comunităților biologice. Odată cu cartea lui V. Volterra, conform multor oameni de știință, a început ecologia matematică modernă.
2. CERCETARE CALITATIVĂ A MODELULUI ELEMENTAL „PRĂDATOR-VICTICĂ”.
2.1 Model de interacțiune trofică în funcție de tipul „prădător-pradă”.
Să luăm în considerare modelul interacțiunii trofice de tip „prădător-pradă”, construit de V. Volterra. Să existe un sistem format din două specii, dintre care una o mănâncă pe cealaltă.
Luați în considerare cazul în care una dintre specii este un prădător, iar cealaltă este o pradă și vom presupune că prădătorul se hrănește numai cu pradă. Să acceptăm următoarea ipoteză simplă:
rata de creștere a victimelor;
Rata de creștere a prădătorilor;
Dimensiunea populației de pradă;
Dimensiunea populației de prădători;
Rata pradă de creștere naturală;
Rata consumului de pradă de către un prădător;
Rata mortalității unui prădător în absența prăzii;
Coeficientul de „prelucrare” a biomasei de pradă de către un prădător în propria sa biomasă.
Apoi, dinamica populației în sistemul prădător-pradă va fi descrisă printr-un sistem de ecuații diferențiale (2.1):
 (2.1)
(2.1)
unde toți coeficienții sunt pozitivi și constanți.
Modelul are o soluție de echilibru (2.2):
Conform modelului (2.1), ponderea prădătorilor în masa totală a animalelor este exprimată prin formula (2.3):
 (2.3)
(2.3)
O analiză a stabilității stării de echilibru în raport cu micile perturbări a arătat că punctul singular (2.2) este stabil „neutru” (de tip „centru”), adică orice abateri de la echilibru nu se sting, ci transferă sistem la un mod oscilator cu o amplitudine în funcție de magnitudinea perturbației. Traiectoriile sistemului pe planul de fază au forma unor curbe închise situate la diferite distanţe de punctul de echilibru (Fig. 1).

Orez. 1 – Faza „portret” a sistemului clasic Volterra „prădător-pradă”
Împărțind prima ecuație a sistemului (2.1) la a doua, obținem ecuația diferențială (2.4) pentru curba pe planul de fază.
 (2.4)
(2.4)
Integrând această ecuație obținem:
![]() (2.5)
(2.5)
unde este constanta integrării, unde 
Este ușor de arătat că mișcarea unui punct de-a lungul planului de fază se va produce doar într-o singură direcție. Pentru a face acest lucru, este convenabil să înlocuiți funcțiile și prin mutarea originii coordonatelor pe plan într-un punct staționar (2.2) și apoi introducerea coordonatelor polare:
 (2.6)
(2.6)
În acest caz, înlocuind valorile sistemului (2.6) în sistemul (2.1), vom avea:
 (2.7)
(2.7)
Înmulțind prima ecuație cu și a doua cu și adunându-le, obținem:
După transformări algebrice similare obținem o ecuație pentru:
Cantitatea, după cum se poate vedea din (4.9), este întotdeauna mai mare decât zero. Astfel, nu se schimbă semnul, iar rotația este totul timpul curge Sens unic.
Integrând (2.9) găsim perioada:
Când sunt mici, atunci ecuațiile (2.8) și (2.9) se transformă în ecuații ale unei elipse. Perioada de circulație în acest caz este egală cu:
 (2.11)
(2.11)
Pe baza periodicității soluțiilor ecuațiilor (2.1), putem obține unele consecințe. Pentru a face acest lucru, să reprezentăm (2.1) sub forma:
 (2.12)
(2.12)
și să integreze pe parcursul perioadei:
 (2.13)
(2.13)
Deoarece substituțiile din și datorate periodicității dispar, mediile perioadei se dovedesc a fi egale cu stările staționare (2.14):
 (2.14)
(2.14)
Cele mai simple ecuații ale modelului „prădător-pradă” (2.1) au o serie de dezavantaje semnificative. Astfel, ei presupun resurse alimentare nelimitate pentru prada și creșterea nelimitată a prădătorului, ceea ce contrazice datele experimentale. În plus, după cum se poate observa din fig. 1, nici una dintre curbele de fază nu se distinge din punct de vedere al stabilității. În prezența unor influențe perturbatoare chiar și mici, traiectoria sistemului se va deplasa din ce în ce mai departe de poziția de echilibru, amplitudinea oscilațiilor va crește, iar sistemul se va prăbuși destul de repede.
În ciuda deficiențelor modelului (2.1), ideile despre natura fundamental oscilativă a dinamicii sistemului „ prădător-pradă» au devenit larg răspândite în ecologie. Interacțiunile prădător-pradă au fost folosite pentru a explica fenomene precum fluctuațiile numărului de animale răpitoare și pașnice din zonele de pescuit, fluctuațiile populațiilor de pești, insecte etc. De fapt, fluctuațiile numărului se pot datora și altor motive.
Să presupunem că în sistemul prădător-pradă există o distrugere artificială a indivizilor ambelor specii și să luăm în considerare întrebarea cum distrugerea indivizilor afectează valorile medii ale numărului lor dacă este efectuată proporțional cu acest număr, cu proporționalitate. coeficienţi şi, respectiv, pentru pradă şi prădător. Ținând cont de ipotezele făcute, rescriem sistemul de ecuații (2.1) sub forma:
 (2.15)
(2.15)
Să presupunem că, adică rata exterminării prăzii este mai mică decât rata creșterii sale naturale. În acest caz, se vor observa și fluctuații periodice ale numerelor. Să calculăm numerele medii:
 (2.16)
(2.16)
Astfel, dacă , atunci dimensiunea medie a populației de pradă crește, iar cea a prădătorului scade.
Să luăm în considerare cazul când coeficientul de exterminare a prăzii este mai mare decât coeficientul de creștere naturală a acesteia, adică. În acest caz ![]() pentru orice , și, prin urmare, soluția primei ecuații (2.15) este mărginită de sus de o funcție descrescătoare exponențial
pentru orice , și, prin urmare, soluția primei ecuații (2.15) este mărginită de sus de o funcție descrescătoare exponențial ![]() , eu mănânc .
, eu mănânc .
Pornind de la un anumit moment de timp t, la care , soluția celei de-a doua ecuații (2.15) începe și ea să scadă și tinde spre zero. Astfel, în cazul în care ambele specii dispar.
2.1 Modele Voltaire generalizate de tip „prădător-pradă”.
Primele modele ale lui V. Volterra, desigur, nu au putut reflecta toate aspectele interacțiunii în sistemul prădător-pradă, deoarece au fost mult simplificate în raport cu condițiile reale. De exemplu, dacă numărul unui prădător este zero, atunci din ecuațiile (1.4) rezultă că numărul de pradă crește la nesfârșit, ceea ce nu este adevărat. Valoarea acestor modele rezidă însă tocmai în faptul că ele au stat la baza pe care ecologia matematică a început să se dezvolte rapid.
Au apărut un număr mare de studii asupra diverselor modificări ale sistemului prădător-pradă, unde s-au construit modele mai generale care țin cont, într-o măsură sau alta, de situația reală din natură.
În 1936 A.N. Kolmogorov a propus folosirea prădătorului-pradă pentru a descrie dinamica sistemului următorul sistem ecuaţie:
 , (2.17)
, (2.17)
unde scade odată cu creșterea numărului de prădători și crește odată cu creșterea numărului de pradă.
Acest sistem de ecuații diferențiale, datorită generalității sale suficiente, face posibilă luarea în considerare a comportamentului real al populațiilor și, în același timp, efectuarea unei analize calitative a soluțiilor sale.
Mai târziu în lucrarea sa, Kolmogorov a explorat în detaliu un model mai puțin general:
 (2.18)
(2.18)
Diverse cazuri speciale ale sistemului de ecuații diferențiale (2.18) au fost studiate de mulți autori. Tabelul prezintă diverse cazuri speciale ale funcțiilor , , .
Tabelul 1 - Diverse modele de comunitate prădător-pradă
| Autorii | |||
| Volterra Lotka | |||
| Gause | |||
| Peaslow | |||
| Holing | |||
| Ivlev | |||
| Royama | |||
| Shimazu | |||
| Mai |
modelare matematică pradă prădător
3. APLICAREA PRACTICĂ A MODELULUI PRĂDATOR-VICTICĂ
Sa luam in considerare model matematic coexistența a două specii (populații) biologice de tip „prădător-pradă”, numite model Volterra-Lotka.
Lasă doi specii biologice trăiesc împreună într-un mediu izolat. Mediul este staționar și oferă cantități nelimitate din tot ceea ce este necesar pentru viață uneia dintre specii, pe care o vom numi victimă. O altă specie, un prădător, se află și ea în condiții staționare, dar se hrănește doar cu indivizii din prima specie. Aceștia ar putea fi carasul și știuca, iepuri de câmp și lupi, șoareci și vulpi, microbi și anticorpi, etc. Pentru claritate, le vom numi caras și știucă.
Sunt specificați următorii parametri inițiali:
De-a lungul timpului, numărul carasului și al știucii se modifică, dar întrucât în baltă sunt mulți pești, nu vom face distincția între 1020 caras și 1021 și de aceea îi vom considera și funcții continue ale timpului t. Vom numi o pereche de numere (,) starea modelului.
Este evident că natura schimbării stării (,) este determinată de valorile parametrilor. Prin modificarea parametrilor și prin rezolvarea sistemului de ecuații ale modelului, este posibil să se studieze modelele schimbărilor de stare sistem ecologic la timp.
Într-un ecosistem, rata de modificare a numărului fiecărei specii va fi de asemenea considerată proporțională cu numărul acesteia, dar numai cu un coeficient care depinde de numărul de indivizi ai altei specii. Deci, la carasul acest coeficient scade odata cu cresterea numarului de stiuci, iar la stiuci creste odata cu cresterea numarului de caras. Vom considera, de asemenea, această dependență ca fiind liniară. Apoi obținem un sistem de două ecuații diferențiale:

Acest sistem de ecuații se numește modelul Volterra-Lotka. Coeficienții numerici , , se numesc parametri de model. Este evident că natura schimbării stării (,) este determinată de valorile parametrilor. Prin modificarea acestor parametri și prin rezolvarea sistemului de ecuații model, este posibil să se studieze modelele de modificări ale stării sistemului ecologic.
Să integrăm ambele ecuații ale sistemului în raport cu t, care se va schimba de la momentul inițial de timp la , unde T este perioada în care au loc schimbări în ecosistem. Să fie în cazul nostru perioada de 1 an. Apoi sistemul ia următoarea formă:
 ;
;
 ;
;
Luând = și = și aducând termeni similari, obținem un sistem format din două ecuații:

Înlocuind datele inițiale în sistemul rezultat, obținem populația de știucă și caras din lac după un an:
Prădătorii pot mânca ierbivore și, de asemenea, prădători slabi. Prădătorii au o gamă largă de hrană și trec ușor de la o pradă la alta, una mai accesibilă. Prădătorii atacă adesea prada slabă. Echilibrul ecologic este menținut între populațiile de pradă-prădători.[...]
Dacă echilibrul este instabil (nu există cicluri limită) sau ciclul extern este instabil, atunci numerele ambelor specii, care experimentează fluctuații puternice, părăsesc vecinătatea echilibrului. Mai mult, degenerarea rapidă (în prima situație) are loc cu o adaptare scăzută a prădătorului, adică. cu mortalitatea sa ridicată (comparativ cu rata de reproducere a victimei). Aceasta înseamnă că un prădător care este slab din toate punctele de vedere nu contribuie la stabilizarea sistemului și el însuși se stinge.[...]
Presiunea prădătorilor este deosebit de puternică atunci când, în coevoluția prădător-pradă, echilibrul se deplasează către prădător și raza de acțiune a prădării se îngustează. Lupta competitivă este strâns legată de lipsa resurselor alimentare poate fi și o luptă directă, de exemplu, a prădătorilor pentru spațiu ca resursă, dar cel mai adesea este pur și simplu deplasarea unei specii care nu are suficientă hrană într-un teritoriu dat de o specie care are suficientă din aceeași cantitate de hrană. Este deja competiţie interspecifică.[ ...]
 |
Și, în sfârșit, în sistemul „prădător-pradă” descris de modelul (2.7), apariția instabilității de difuzie (cu stabilitate de echilibru local) este posibilă numai în cazul în care mortalitatea naturală a prădătorului crește odată cu creșterea populației sale mai rapid decât funcție liniară, iar funcția trofică diferă de cea a lui Volterra sau când populația de pradă este o populație de tip Ollie [...]
Teoretic, în modelele „un prădător - două pradă”, pășunatul echivalent (lipsa preferinței pentru una sau alta specie de pradă) poate afecta coexistența competitivă a speciilor de pradă doar în acele locuri în care există deja un echilibru potențial stabil. Diversitatea poate crește doar în condițiile în care speciile cu o capacitate competitivă mai mică au o rată de creștere a populației mai mare decât speciile dominante. Acest lucru ne permite să înțelegem situația când pășunatul uniform duce la o creștere a diversității speciilor de plante unde număr mai mare speciile care au fost selectate pentru reproducere rapidă coexistă cu specii a căror evoluție vizează creșterea competitivității.[...]
În mod similar, selecția de pradă dependentă de densitate poate duce la un echilibru stabil în modelele teoretice ale două specii de pradă concurente în care nu exista niciun echilibru anterior. Pentru a face acest lucru, prădătorul ar trebui să fie capabil de răspunsuri funcționale și numerice la modificările densității prăzii; este posibil, totuși, ca comutarea (atacuri disproporționat de frecvente asupra celei mai abundente pradă) să aibă mai multe important. De fapt, s-a stabilit că comutarea are un efect stabilizator în sistemele „un prădător - n pradă” și reprezintă singurul mecanism capabil să stabilizeze interacțiunile în cazurile în care nișele de pradă se suprapun complet. Prădătorii nespecializați pot juca un astfel de rol. Preferința prădătorilor mai specializați pentru un competitor dominant acționează în același mod ca schimbarea prădătorilor și poate stabiliza interacțiunile teoretice în modele în care anterior nu exista un echilibru între speciile de pradă, cu condiția ca nișele lor să fie într-o oarecare măsură separate.[...]
De asemenea, un prădător „puternic din toate punctele de vedere” nu stabilizează comunitatea, adică. bine adaptat la o pradă dată și cu mortalitate relativă scăzută. În acest caz, sistemul are un ciclu limită instabil și, în ciuda stabilității poziției de echilibru, degenerează într-un mediu aleatoriu (prădătorul mănâncă prada și ca urmare moare). Această situație corespunde unei degenerescențe lente.[...]
Astfel, cu o bună adaptare a unui prădător în vecinătatea unui echilibru stabil, pot apărea cicluri instabile și stabile, i.e. în funcție de condițiile inițiale, sistemul „prădător-pradă” fie tinde spre echilibru, fie, oscilând, se îndepărtează de acesta, fie se stabilesc fluctuații stabile ale numărului ambelor specii în vecinătatea echilibrului [...]
Organismele care sunt clasificate drept prădători se hrănesc cu alte organisme, distrugându-le prada. Astfel, printre organismele vii ar trebui să se distingă încă un sistem de clasificare, și anume „prădători” și „pradă”. Relațiile dintre astfel de organisme s-au dezvoltat de-a lungul evoluției vieții de pe planeta noastră. Organismele prădătoare acționează ca regulatori naturali ai numărului de organisme pradă. O creștere a numărului de „prădători” duce la o scădere a numărului de „pradă”, aceasta, la rândul său, reduce aprovizionarea cu hrană („pradă”) pentru „prădători”, ceea ce dictează în general o scădere a numărului. de „pradă” etc. Astfel, în biocenoză se produc constant fluctuații ale numărului de prădători și pradă, dar în general se stabilește un anumit echilibru pentru o anumită perioadă de timp într-un interval destul de conditii stabile mediu inconjurator.[...]
În cele din urmă, se ajunge la un echilibru ecologic între populațiile de prădători și de pradă.[...]
Pentru o funcție trofică de al treilea tip, starea de echilibru va fi stabilă dacă unde N este punctul de inflexiune al funcției (vezi Fig. 2, c). Aceasta rezultă din faptul că pe interval funcția trofică este concavă și, prin urmare, ponderea relativă a consumului de pradă de către prădător crește.[...]
Fie Гг = -Г, adică. există o comunitate de tip „prădător-pradă”. În acest caz, primul termen din expresia (7.4) este egal cu zero, iar pentru a satisface condiția de stabilitate în ceea ce privește probabilitatea stării de echilibru N, se cere ca nici cel de-al doilea termen să nu fie pozitiv.[.. .]
Astfel, pentru comunitatea considerată prădător-pradă, putem concluziona că poziția generală pozitivă de echilibru este asimptotic stabilă, adică pentru orice date inițiale 1H(0)>0, evoluția are loc în așa fel încât N(7) - ■ K la cu condiția ca N >0.[...]
Astfel, într-un mediu omogen care nu are adăpost pentru reproducere, prădătorul, mai devreme sau mai târziu, distruge populația de pradă și apoi se stinge singur. Valurile vieții” (modificări ale abundenței prădătorului și a prăzii) se succed cu o schimbare constantă de fază și, în medie, abundența atât a prădătorului, cât și a prăzii rămâne aproximativ la același nivel. Durata perioadei depinde de ritmurile de creștere ale ambelor specii și de parametrii inițiali. Pentru populația de pradă, influența prădătorului este pozitivă, deoarece reproducerea lui excesivă ar duce la prăbușirea populației sale. La rândul lor, toate mecanismele care împiedică exterminarea completă a prăzii contribuie la păstrarea rezervei de hrană a prădătorului.[...]
Alte modificări pot fi o consecință a comportamentului prădătorului. Numărul de indivizi pradă pe care un prădător este capabil să le consume timp dat, are limita ei. Efectul saturației prădătorilor la apropierea acestui prag este prezentat în tabel. 2-4, B. Interacțiunile descrise de ecuațiile 5 și 6 pot avea puncte de echilibru stabile sau pot prezenta fluctuații ciclice. Totuși, astfel de cicluri sunt diferite de cele reflectate în ecuațiile Lotka-Volterra 1 și 2. Ciclurile transmise de ecuațiile 5 și 6 pot avea amplitudine constantă și densități medii atâta timp cât mediul este constant; după ce a apărut o perturbare, pot reveni la amplitudinile și densitățile medii anterioare. Astfel de cicluri care se recuperează după perturbări sunt numite cicluri limită stabile. Interacțiunea dintre un iepure de câmp și un râs poate fi considerată un ciclu limită stabil, dar nu este un ciclu Lotka-Volterra.[...]
Să luăm în considerare apariția instabilității difuziei în sistemul prădător-pradă, dar mai întâi vom scrie condițiile care asigură apariția instabilității difuziei în sistemul (1.1) cu n = 2. Este clar că echilibrul (N, N). ) este local (adică[ .. .]
Să trecem la interpretarea cazurilor asociate cu coexistența pe termen lung a prădător și pradă. Este clar că în absența ciclurilor limită, un echilibru stabil va corespunde într-un mediu aleatoriu fluctuațiilor populației, iar amplitudinea acestora va fi proporțională cu dispersia perturbațiilor. Acest fenomen se va produce dacă prădătorul are o mortalitate relativă ridicată și în același timp un grad ridicat de adaptabilitate la o anumită pradă.[...]
Să luăm acum în considerare modul în care dinamica sistemului se schimbă odată cu creșterea aptitudinii prădtorului, adică cu b descrescând de la 1 la 0. Dacă fitness-ul este suficient de scăzut, atunci nu există cicluri limită, iar echilibrul este instabil. Odată cu o creștere a fitnessului în vecinătatea acestui echilibru, poate apărea un ciclu stabil și apoi unul extern instabil. În funcție de condițiile inițiale (raportul dintre biomasa prădătorului și pradă), sistemul poate pierde stabilitatea, adică părăsesc vecinătatea echilibrului, sau se vor stabili în acesta oscilații stabile în timp. Creșterea în continuare a fitnessului face imposibilă natura oscilativă a comportamentului sistemului. Cu toate acestea, când b [...]
Un exemplu de feedback negativ (stabilizator) este relația dintre prădător și pradă sau funcționarea sistemului de carbonat oceanic (soluție de CO2 în apă: CO2 + H2O -> H2CO3). De obicei, cantitatea de dioxid de carbon dizolvată în apa oceanului este în echilibru parțial cu concentrația de dioxid de carbon din atmosferă. Creșterile locale ale dioxidului de carbon din atmosferă după erupțiile vulcanice duc la o intensificare a fotosintezei și la absorbția acesteia de către sistemul carbonatului oceanic. Pe măsură ce nivelurile de dioxid de carbon din atmosferă scad, sistemul de carbonat oceanic eliberează CO2 în atmosferă. Prin urmare, concentrația de dioxid de carbon din atmosferă este destul de stabilă.[...]
[ ...]
După cum a remarcat R. Ricklefs (1979), există factori care contribuie la stabilizarea relațiilor în sistemul „prădător-pradă”: ineficiența prădătorului, disponibilitatea resurselor alimentare alternative pentru prădător, reducerea întârzierii reacția prădătorului, precum și restricțiile de mediu impuse Mediul extern pentru o populatie sau alta. Interacțiunile dintre populațiile de prădători și pradă sunt foarte variate și complexe. Astfel, dacă prădătorii sunt suficient de eficienți, ei pot regla densitatea populației de pradă, menținând-o sub capacitatea de transport a mediului. Prin influenta pe care o au asupra populatiilor de prada, pradatorii influenteaza evolutia diferitelor caracteristici ale prazii, ceea ce duce in final la echilibrul ecologic intre populatiile de prada si prada.[...]
Dacă una dintre condiții este îndeplinită: 0 1/2. Dacă 6 > 1 (kA [...]
Stabilitatea biotei și a mediului depinde doar de interacțiunea plantelor - autotrofe și organisme heterotrofe erbivore. Prădătorii de orice dimensiune nu sunt capabili să perturbe echilibrul ecologic al comunității, deoarece în conditii naturale nu își pot crește numărul dacă numărul victimelor rămâne constant. Prădătorii nu numai că trebuie să fie ei înșiși mobili, dar se pot hrăni doar cu animalele în mișcare.[...]
Niciun alt pește nu este la fel de răspândit ca știuca. În câteva zone de pescuit din rezervoare în picioare sau curgătoare, nu există presiune din partea știucilor pentru a menține echilibrul între pradă și prădător. lor. Știucile sunt excepțional de bine reprezentate în lume. Sunt prinși în toată emisfera nordică din Statele Unite și Canada până la America de Nord, prin Europa până în nordul Asiei.[...]
O altă posibilitate de conviețuire durabilă apare aici, într-o gamă restrânsă de adaptare relativ ridicată. La trecerea la un regim instabil cu un prădător foarte „bun”, poate apărea un ciclu limită extern stabil, în care disiparea biomasei este echilibrată de afluxul acesteia în sistem (productivitate ridicată a prăzii). Atunci apare o situație curioasă în care cele mai probabile două sunt valori caracteristice amplitudini ale oscilațiilor aleatorii. Unele apar în apropierea echilibrului, altele - în apropierea ciclului limită și sunt posibile tranziții mai mult sau mai puțin frecvente între aceste regimuri.[...]
Populații ipotetice care se comportă conform vectorilor din Fig. 10.11 A, sunt prezentate în Fig. 10.11,-B folosind un grafic care arată dinamica raportului dintre populațiile de prădători și pradă și în Fig. 10.11.5 sub forma unui grafic al dinamicii abundenței prădătorului și a prăzii în timp. În populația de pradă, pe măsură ce trece de la un echilibru cu densitate scăzută la un echilibru cu densitate mare și se întoarce înapoi, are loc o „explozie” de numere. Și această creștere a numărului nu este o consecință a unei schimbări la fel de pronunțate mediu inconjurator. Dimpotrivă, această modificare a numerelor este generată de impactul în sine (cu un nivel mic de „zgomot” în mediu) și reflectă, în special, existența mai multor stări de echilibru. Un raționament similar poate fi folosit pentru a explica mai multe cazuri complexe dinamica populației în populațiile naturale.[...]
Cea mai importantă proprietate a unui ecosistem este stabilitatea acestuia, echilibrul schimburilor și procesele care au loc în el. Capacitatea populațiilor sau ecosistemelor de a menține un echilibru dinamic stabil în condițiile de mediu în schimbare se numește homeostazie (homoios - același, similar; stază - stare). Homeostazia se bazează pe principiul feedback-ului. Menținerea echilibrului în natură nu necesită control extern. Un exemplu de homeostazie este subsistemul „prădător-pradă”, în care densitatea populației de prădător și pradă este reglementată.[...]
Ecosistem natural(biogeocenoza) funcționează stabil cu interacțiunea constantă a elementelor sale, circulația substanțelor, transferul de energie și informații chimice, energetice, genetice și de altă natură prin lanțuri-canale. Conform principiului echilibrului, orice sistem natural cu un flux de energie și informații care trece prin el tinde să dezvolte o stare de echilibru. În același timp, sustenabilitatea ecosistemelor este asigurată automat printr-un mecanism de feedback. Feedback-ul constă în utilizarea datelor primite de la componentele gestionate ale ecosistemelor pentru a face ajustări ale procesului de către componentele de gestionare. Relația „prădător”-„pradă” discutată mai sus în acest context poate fi descrisă ceva mai detaliat; da, într-un ecosistem acvatic pești răpitori(știucă într-un iaz) mănâncă alte specii de pești pradă (crap); dacă numărul carasului crește, acesta este un exemplu de feedback pozitiv; știuca, hrănindu-se cu caras, își reduce numărul - acesta este un exemplu de feedback negativ; pe măsură ce numărul prădătorilor crește, numărul victimelor scade, iar prădătorul, întâmpinând o lipsă de hrană, își reduce și creșterea populației; in final, in balta in cauza se stabileste un echilibru dinamic in numarul atat de stiuca cat si de caras. Echilibrul este menținut în mod constant, ceea ce ar exclude dispariția oricărei legături lanț trofic(Fig. 64).[...]
Să trecem la cea mai importantă generalizare, și anume că interacțiunile negative devin mai puțin vizibile în timp dacă ecosistemul este suficient de stabil și structura spatiala oferă posibilitatea adaptării reciproce a populaţiilor. În sistemele model de tip prădător-pradă descrise de ecuația Lotka-Volterra, dacă în ecuație nu sunt introduși termeni suplimentari care caracterizează acțiunea factorilor autolimitatori ai numerelor, atunci oscilațiile au loc continuu și nu se sting (vezi Lewontin , 1969). Pimentel (1968; vezi și Pimentel și Stone, 1968) a arătat experimental că astfel de termeni suplimentari pot reflecta adaptări reciproce sau feedback genetic. Când au fost create culturi noi din indivizi care au coexistat anterior doi ani într-o cultură în care numărul lor a fost supus unor fluctuații semnificative, s-a dovedit că au dezvoltat homeostazie ecologică, în care fiecare dintre populații a fost „suprimată” de cealaltă la astfel de într-o măsură în care s-a dovedit posibilă coexistența lor la un echilibru mai stabil.





