Plan - Geometrie descriptivă. Probleme cu un plan Liniile principale dintr-un plan

Semnele de apartenență sunt bine cunoscute din cursul de planimetrie. Sarcina noastră este să le luăm în considerare în raport cu proiecțiile obiectelor geometrice.

Un punct aparține unui plan dacă aparține unei linii situate în acest plan.

Apartenența la un plan drept este determinată de unul dintre cele două criterii:

a) o dreaptă trece prin două puncte situate în acest plan;

b) o dreaptă trece printr-un punct și este paralelă cu liniile situate în acest plan.

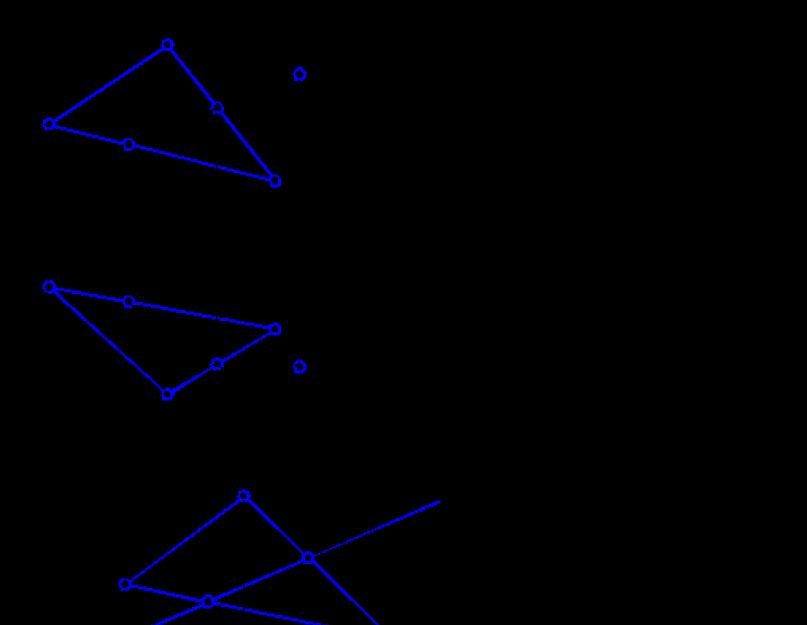
Folosind aceste proprietăți, să rezolvăm problema ca exemplu. Fie ca planul să fie definit printr-un triunghi ABC. Este necesar să se construiască proiecția lipsă D 1 puncte D aparținând acestui plan. Succesiunea construcțiilor este următoarea (Fig. 2.5).

Prin punct D 2 efectuăm o proiecție în linie dreaptă d, întins în avion DABC, intersectând una dintre laturile triunghiului și punctul O 2. Atunci punctul 1 2 aparține dreptelor O 2 D 2 și C 2 ÎN 2. Prin urmare, putem obține proiecția sa orizontală 1 1 pe C 1 ÎN 1 prin linia de comunicare. Punctele de legătură 1 1 și O 1, obținem o proiecție orizontală d 1. Este clar că ideea D 1 îi aparține și se află pe linia de legătură de proiecție cu punctul D 2 .

Problemele de a determina dacă îi aparține un punct sau un plan drept sunt rezolvate destul de simplu. În fig. Figura 2.6 prezintă progresul în rezolvarea unor astfel de probleme. Pentru claritatea prezentării problemei, definim planul printr-un triunghi.

Orez. 2.6. Probleme pentru a determina dacă un punct aparține unui plan drept.

Pentru a determina dacă un punct îi aparține E avion DABC, trageți o linie dreaptă prin proiecția sa frontală E 2 O 2. Presupunând că linia dreaptă a aparține planului DABC, să-i construim proiecția orizontală O 1 la punctele de intersecție 1 și 2. După cum vedem (Fig. 2.6, a), drept O 1 nu trece prin punct E 1. Prin urmare, punctul E ÏDABC.

În problema apartenenţei la o linie V planuri triunghiulare ABC(Fig. 2.6, b), este suficient să folosiți una dintre proiecțiile în linie dreaptă V 2 construi un altul V 1 * având în vedere că ВÌDAВС. După cum vedem, V 1* și V 1 nu se potrivesc. Prin urmare, drept în Ë DABC.

Linii de nivel într-un plan

Definiția liniilor de nivel a fost dată mai devreme. Se numesc linii de nivel aparținând unui plan dat principal . Aceste linii (linii drepte) joacă un rol semnificativ în rezolvarea unui număr de probleme de geometrie descriptivă.

Să luăm în considerare construirea unor linii de nivel în planul definit de triunghi (Fig. 2.7).

Orez. 2.7. Construirea liniilor principale ale unui plan definit printr-un triunghi

Plan orizontal DABCîncepem prin a desena proiecția sa frontală h 2, despre care se știe că este paralelă cu axa OH. Deoarece această linie orizontală aparține acestui plan, trece prin două puncte ale planului DABC, și anume, puncte Oși 1. Având proiecțiile lor frontale O 2 și 1 2, prin linia de comunicație obținem proiecții orizontale ( O 1 există deja) 1 1 . Conectarea punctelor O 1 și 1 1 , avem o proiecție orizontală h 1 plan orizontal DABC. Proiecția profilului h 3 planuri orizontale DABC va fi paralel cu axa OH prin definitie.

Avionul frontal DABC este construit într-un mod similar (Fig. 2.7), cu singura diferență că desenul său începe cu o proiecție orizontală f 1, deoarece se știe că este paralelă cu axa OX. Proiecția profilului f 3 fronturi trebuie să fie paralele cu axa OZ și să treacă prin proiecții CU 3, 2 3 din aceleași puncte CUși 2.

Linia de profil a planului DABC are o orizontală r 1 si fata r 2 proiecții paralele cu axele OYŞi OZ, și proiecția profilului r 3 poate fi obținut din față folosind puncte de intersecție ÎNși 3 s D ABC.

Aparținând unui plan drept:

2) o dreaptă aparține unui plan dacă trece printr-un punct aparținând unui plan dat și este paralelă cu o dreaptă a acestui plan.

Din aceste două semne de apartenență la un plan drept se pot trage următoarele concluzii:

1) dacă un plan este dat de urme, atunci linia aparține planului dacă urmele dreptei se află pe urme cu același nume de pe plan;

2) o dreaptă aparține unui plan dacă are un punct comun cu o urmă a planului și este paralelă cu cealaltă urmă.

Se consideră planul Q, în poziție generală, definit de urme (Figura 17). Linia dreaptă NM aparține acestui plan, deoarece urmele sale se află pe urmele planelor cu același nume.

Figura 18 prezintă planul definit de liniile de intersectare t și n. Pentru a construi o linie dreaptă situată în acest plan, este suficient să desenați în mod arbitrar una dintre proiecții, de exemplu, orizontală c1, și apoi să proiectați punctele de intersecție ale acestei linii cu liniile drepte ale planului pe planul frontal. Proiecția frontală a dreptei c2 va trece prin punctele obținute.

Figura 17 Figura 18

Conform celei de-a doua poziții, o dreaptă h aparținând planului P este construită în figura 19 - are un punct N (N1, N2) în comun cu planul P și este paralelă cu o dreaptă situată în plan - urmă orizontală P1.

Figura 19 Figura 20

Să luăm în considerare planuri cu o anumită poziție. Dacă o linie dreaptă sau o figură aparține unui plan care se proiectează orizontal (Figura 20), atunci proiecțiile orizontale ale acestor elemente geometrice coincid cu urma orizontală a planului.

Dacă o figură dreaptă sau plată aparține unui plan care se proiectează frontal, atunci proiecțiile frontale ale acestor elemente geometrice coincid cu urma frontală a planului.

Apartenența unui punct la plan:

Un punct aparține unui plan dacă aparține unei linii situate în acest plan.

Exemplu: dat un plan P (a || b). Proiecția orizontală a punctului B, aparținând planului P, este cunoscută Aflați proiecția frontală a punctului B (Figura 21).

Figurile 22, 23, 24 arată o soluție fragmentară la această problemă:

1) trageți orice linie dreaptă prin B1 (proiecția cunoscută a punctului B),

situată în planul P - pentru aceasta, linia dreaptă trebuie să aibă două puncte comune cu planul. Să le marchem pe desen - M1 și K1;

2) construiți proiecțiile frontale ale acestor puncte pe baza faptului că punctele aparțin unor drepte, adică M2 pe linia a, K2 pe linia b. Să desenăm o proiecție frontală a unei drepte prin proiecțiile frontale ale punctelor;

Figura 21 Figura 22

rezumatul altor prezentări

„Determinarea unghiurilor diedrice” - O linie dreaptă trasată într-un plan dat. Să aruncăm o grindă. Baza piramidei. Unghiuri diedrice în piramide. Sarcină. Punctul K. Rezolvarea problemelor. Definiţie. Romb. Planuri perpendiculare. Găsiți unghiul diedrului. Să construim BK. Punctele M și K se află pe fețe diferite. Punctul M este situat pe una dintre fețele unui unghi diedru egal cu 30. Definiție și proprietăți. Construcția unui unghi liniar. Găsiți unghiul. Desenați o perpendiculară.

„Axiome de bază ale stereometriei” - Primele lecții de stereometrie. Avion. Geometrie. Un vechi proverb chinezesc. Corolare din axiomele stereometriei. Imagini cu figuri spațiale. Subiect de stereometrie. Punctele unei linii drepte se află într-un plan. Patru triunghiuri echilaterale. Axiomele stereometriei. Corolare din axiome. Axiomă. Piramida lui Keops. Avioanele au un punct comun. Corpuri geometrice. Figuri de bază în spațiu. Surse și link-uri.

„Conceptul de piramidă” - Unghiuri egale. Modelul unei întreprinderi industriale moderne. Piramidele în chimie. Piramida în geometrie. Călătorește în jurul lumii. Secțiuni ale unei piramide pe planuri. Traseul de călătorie. Proiecții. Piramidele egiptene. Baza piramidei. Urma secțiunii. Coastă laterală. Piramida corectă. O călătorie virtuală în lumea piramidelor. Întrebări de testare. Fețe laterale adiacente. Minunile din Giza. Piramide în trepte. Poliedru.

„Sistemul cartezian” – Definiția unui sistem cartezian. Conceptul de sistem de coordonate. Coordonatele oricărui punct. Sistemul de coordonate carteziene. Sistem de coordonate dreptunghiular. Introducerea coordonatelor carteziene în spațiu. Coordonatele punctului. Rene Descartes. Întrebări de completat. Coordonatele vectoriale.

„Exemple de simetrie în natură” - Simetrie discretă. Exemple de distribuție simetrică. Simetrie în natură. Simetria formei exterioare a cristalului. Simetria cilindrului. Tipuri de simetrie. Obiecte naturale. Ce este simetria. Simetria este o proprietate fundamentală a naturii. Simetria în geografie. Simetria în biologie. Oamenii, multe animale și plante au simetrie bilaterală. Simetria în geologie. Simetria în fizică.

„Probleme cu paralelograme” - Centrele cercurilor. Perimetrul unui paralelogram. Aria unui paralelogram. Egalitatea segmentelor. Unghi ascuțit. Două cercuri. Proprietatea unui paralelogram. Linia de mijloc. Unghiuri. Semne ale unui paralelogram. Pătrat. Patrulater. Parte. Triunghiuri. Puncte. Tangent la un cerc. Dovada. Proprietățile unui paralelogram. Înălțimea paralelogramului. Diagonală. Geometrie. Cerc. Diagonalele unui paralelogram.

Definiţie. O dreaptă și un plan se numesc paralele dacă nu au puncte comune (a ||)

Un semn de paralelism între o dreaptă și un plan.

Teorema. Dacă o dreaptă care nu se află într-un plan dat este paralelă cu o dreaptă care se află în acest plan, atunci este paralelă cu planul însuși.

Concluzii.

Cazuri de poziție relativă a unei drepte și a unui plan:

A) linia dreaptă se află în plan;
b) o dreaptă și un plan au un singur punct comun;
c) o dreaptă și un plan nu au un singur punct comun.

Cazuri de aranjare reciprocă a avioanelor:

Proprietățile planurilor paralele:

Probleme și teste pe tema „Tema 3. „Paralelismul unei drepte și al unui plan; paralelismul planurilor”.

Paralelismul planurilor
Lecții: 1 Teme: 8 Teste: 1
Paralelism de drepte, drepte și plan - Paralelism de drepte și plane, nota 10
Semne de paralelism a două drepte. Axioma dreptelor paralele - linii paralele gradul 7
Lecții: 2 Teme: 11 Teste: 1
Poziția relativă a liniilor în spațiu. Unghiul dintre liniile drepte - Paralelism de drepte și plane, nota 10
Lecții: 1 Teme: 9 Teste: 1
Perpendicularitatea unei drepte și a unui plan - Perpendicularitatea dreptelor si a planurilor, nota 10
Lecții: 1 Teme: 10 Teste: 1

Subiectul „Axiomele stereometriei” joacă un rol important în dezvoltarea conceptelor spațiale, așa că încercați să implicați mai multe modele (carton și ace de tricotat) și desene.

Tema „Paralelism în spațiu” oferă cunoștințe despre paralelismul dreptelor și planurilor în spațiu. Acest material rezumă informațiile cunoscute din planimetrie despre paralelismul dreptelor. Folosind exemplul teoremei privind existența și unicitatea unei drepte paralele cu una dată, vă faceți o idee despre necesitatea de a redovedi faptele cunoscute din planimetrie în cazurile în care vorbim despre puncte și drepte în spațiu , și nu despre un anumit avion.

Problemele de demonstrare sunt rezolvate în multe cazuri prin analogie cu teoremele de demonstrare. Pentru a rezolva problemele de calcul a lungimilor segmentelor, este necesar să se repete cursul planimetriei: egalitatea și asemănarea triunghiurilor, definițiile, proprietățile și caracteristicile unui dreptunghi, paralelogram, romb, pătrat, trapez.

Un punct aparține unei linii dacă proiecțiile sale se află pe proiecțiile cu același nume de pe această dreaptă (Fig. 21a).

Un punct aparține unui plan dacă se află pe o dreaptă situată în acest plan (Fig. 21b).

O dreaptă aparține unui plan dacă trece prin două puncte situate în acest plan (Fig. 21c).

O linie este paralelă cu un plan dacă este paralelă cu orice dreaptă situată în acel plan. Figura 22 prezintă o dreaptă t paralelă cu o dreaptă b aparținând planului Σ: t // b О Σ (aÇ b).

Figura 22

Prin orice punct din spațiu puteți desena un număr infinit de drepte paralele cu un plan dat.

Aceasta este o sarcină pentru a determina punctul comun al unei linii și al unui plan. Se mai numește și punctul de întâlnire. Să considerăm intersecția unei drepte cu un plan de o anumită poziție.

Planul Σ este definit de triunghiul ABC și este un plan proiectat orizontal. Punctul de întâlnire al dreptei k cu planul Σ este determinat de proiecția orizontală. Proiecția frontală a punctului K este finalizată folosind o linie de comunicație. Notația simbolică va arăta astfel: k Ç Σ (ABC) = K.

Vizibilitatea liniei în raport cu planul este determinată folosind punctele 1 și 2 concurente frontal.

Figura 23

Intersecția unei linii cu un plan general este prezentată în Figura 24. În acest caz, este necesar să se încadreze linia în planul de proiectare.

tО Σ ^ П 2 - linie dreaptă t aparține planului Σ, care este perpendicular pe planul orizontal al proiecțiilor. Linia de intersecție a acestui plan cu acesta este linia (1, 2). Apoi se găsește punctul de intersecție al acestei drepte cu linia dreaptă t, care va fi punctul de întâlnire al dreptei și al planului. Vizibilitatea unei linii în raport cu un plan este determinată folosind puncte concurente. Să luăm punctele 3 și 4 concurente orizontal. Deoarece punctul 3, care aparține dreptei, s-a dovedit a fi mai jos decât punctul 4, prin urmare, linia de pe planul orizontal din dreapta punctului de intersecție este invizibilă. Apoi luăm punctele 1 și 5 concurente frontal. Punctul 1, care aparține planului, se află mai aproape, prin urmare, linia dreaptă este în spatele planului și este invizibilă pe proiecția frontală de la punctul 1 la punctul K.

Figura 24

Liniile drepte speciale aparținând planului includ liniile drepte orizontale, frontale și de profil. Construcția acestor linii este utilizată în rezolvarea multor probleme din geometria descriptivă. Imaginea lor este dată în Figura 25. Mai mult, pe plan orizontal orizontală are o dimensiune naturală, pe plan frontal - frontalul și pe planul profilului - linia dreaptă a profilului.

Figura 25