Munca practica
matematică
1. Găsirea limitei unei funcții. Prima și a doua sunt limite minunate.
2. Derivata unei functii complexe. Studiul unei funcții a unei variabile și reprezentarea graficelor.
3. Testul „Aplicarea calculului diferențial la studiul funcțiilor.”
4. Aflarea integralelor nedefinite. Calculul integralelor definite.
5. Calculul determinanților.
6. Rezolvarea sistemelor de ecuații liniare folosind metoda Cramer. Test.
7. Rezolvarea problemelor pe tema „Seturi”. Formule de algebră logică.
8. Calculul probabilităților de evenimente aleatoare. Formula probabilității totale.
9. Calculul caracteristicilor numerice.
10. Testul „Fundamentele teoriei probabilităților și statisticii matematice”
11. Forma trigonometrică a unui număr complex.
12. Acțiuni cu numere complexe sub diverse forme.
INSTRUCȚIUNI METODOLOGICE PENTRU LUCRĂRI PRACTICE LA MATEMATICĂ
CURS 2
O lecție practică este o formă de organizare a procesului educațional, care implică elevii să efectueze una sau mai multe lucrări practice la sarcină și sub îndrumarea unui profesor.
Astfel, la orele practice de matematică, elevii își dezvoltă capacitatea de a rezolva probleme, care în viitor ar trebui să fie folosită pentru rezolvarea problemelor profesionale la discipline speciale.
În cursul lucrărilor practice, studenții stăpânesc capacitatea de a utiliza surse de informații, de a lucra cu documente normative și materiale de instruire, cărți de referință, de a realiza desene, diagrame, tabele, de a rezolva diferite tipuri de probleme și de a face calcule.
Probleme care sunt rezolvate în timpul lecțiilor practice de matematică:
1) extinderea și consolidarea cunoștințelor teoretice în matematică dobândite în timpul prelegerilor;
2) dezvoltarea la elevi a abilităţilor practice şi a abilităţilor necesare rezolvării cu succes a problemelor de matematică;
3) dezvoltarea nevoii de autoeducare a elevilor și îmbunătățirea cunoștințelor și abilităților în procesul de studiere a matematicii;
4) formarea unei atitudini creative și a unei abordări de cercetare în procesul studierii matematicii;
5) formarea calităților semnificative din punct de vedere profesional ale unui viitor specialist și abilități în aplicarea cunoștințelor dobândite în domeniul profesional.
Lecția practică nr. 1. Calculul limitelor funcției. Prima și a doua sunt limite minunate.
Subiect : Calculul limitelor funcției.
Ţintă: însuşirea unor cunoştinţe de bază în domeniul ramurilor fundamentale ale matematicii . Testarea asimilării cunoștințelor privind calculul limitelor funcțiilor. Repetă și sistematizează cunoștințele pe această temă.
Sarcini:
Dezvoltarea gândirii profesionale creative;
Stăpânirea limbajului științei, abilități de operare a conceptelor;
Stăpânirea abilităților de stabilire și rezolvare a problemelor;
Aprofundarea pregătirii teoretice și practice;
Dezvoltarea inițiativei și a independenței elevilor.
Consolidarea abilităților de calcul;
Continuați să lucrați la vorbirea matematică.
Formarea abilităților pentru munca independentă, lucrul cu un manual, abilități pentru dobândirea independentă a cunoștințelor;
Dezvoltarea capacității de a evidenția principalul lucru atunci când lucrați cu text;
Formarea gândirii independente, operații mentale: comparație, analiză, sinteză, generalizare, analogie;
Arătați elevilor rolul muncii sistematice pentru aprofundarea și creșterea forței cunoștințelor, asupra culturii îndeplinirii sarcinilor;
Dezvoltarea abilităților creative ale elevilor.
Furnizarea de lucrări practice:
Material teoretic de recomandări metodologice pentru lucrări practice.
Matematică, – Seria: Învățământul secundar profesional. - Rostov-pe-Don „Phoenix”, p.
Progresul lecției practice.
1.Formularea temei lecției, explicarea legăturii temei cu alte subiecte ale disciplinei academice;
2. Verificarea gradului de pregătire a elevilor pentru curs;
3. Desfășurarea lecției propriu-zise conform temei și în conformitate cu programul de lucru al disciplinei:
Studiați materiale teoretice pe tema „Calculul limitelor funcțiilor”.
Luați în considerare exemple de rezolvare a sarcinilor tipice.
Efectuați lucrări independente privind calcularea limitelor funcțiilor folosind prima și a doua limite remarcabile.
Răspunde la întrebări de securitate.
Informații teoretice și recomandări metodologice
privind rezolvarea problemelor.
1. Prezentarea materialului teoretic.
Pentru a calcula limita unei funcții într-un punct, trebuie să:
1) Înlocuiți în loc de variabila x ceea ce tinde x.
2) Dacă după finalizarea pasului 1) obținem o incertitudine a formularului https://pandia.ru/text/78/405/images/image003_6.png" width="19" height="22 src=">și înlocuiți săgeata cu minus: (x-a).
3) Dacă, după parcurgerea pasului 1, primim o incertitudine a formularului https://pandia.ru/text/78/405/images/image002_13.png" width="18" height="31 src="> asociate cu valorile funcțiilor trigonometrice, trebuie să folosim prima limită remarcabilă.
Definiție. Prima limită remarcabilă se numește limită
https://pandia.ru/text/78/405/images/image007_4.png" alt="$\displaystyle \lim_(x\to0)\dfrac(\sin x)(x)=1. $" width="102" height="52">!}
5) Definiție:A doua limită remarcabilă numită limită

Numărul dat de această limită joacă un rol foarte important atât în analiza matematică, cât și în alte ramuri ale matematicii. Numărul este sunat baza logaritmilor naturali ( https://pandia.ru/text/78/405/images/image009_4.png" alt="$ e$" width="11" height="14">показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:!}
![]()
2. Consolidarea materialului studiat.
Exemplul 1
https://pandia.ru/text/78/405/images/image015_1.png" width="28" height="30 src=">= -4
Am folosit regula 1) și am înlocuit în loc de x ceea ce ar trebui să încerce x, adică x=2.
Exemplul 2
https://pandia.ru/text/78/405/images/image017_1.png" width="154" height="32 src=">.png" width="21" height="30 src=">= 5
Exemplul 3
https://pandia.ru/text/78/405/images/image021_1.png" width="199" height="37 src=">.png" width="137" height="35 src=">. png" width="138" height="24 src=">=3+3=6
Exemplul 4
https://pandia.ru/text/78/405/images/image004_7.png" width="22" height="31 src=">.png" width="104" height="46 src=">. png" height="30 src=">
Exemplul 5
https://pandia.ru/text/78/405/images/image032_0.png" width="61" height="46 src=">.png" height="30 src=">=2
Exemplul 6
https://pandia.ru/text/78/405/images/image036_0.png" width="18" height="28 src=">
b) 
V) 
3. Consolidarea cunoștințelor, aptitudinilor și abilităților.
Efectuați lucrări independente privind calcularea limitelor funcțiilor.
Lucrarea practică nr. 1. Opțiunea 1 Calculați limita funcției: 1. 2. 3. 10. | Lucrarea practică nr. 1. Opțiunea 2 Calculați limita funcției: 1. 2. 3. 10. |
Lucrarea practică nr. 2.
Subiect : Găsirea derivatei unei funcții. Studiul unei funcții a unei variabile și trasarea unui grafic.
Ţintă : Testează în practică cunoștințele despre conceptul de derivată a unei funcții, capacitatea de a găsi derivate ale funcțiilor elementare, funcții complexe, funcții inverse, folosind tabelul de derivate și regulile de diferențiere, conceptul de funcție complexă și inversă, capacitatea a folosi o derivată pentru a studia funcțiile.
Furnizarea de lucrări practice:
Manual. "Matematică". – M.: Dropia, 2010.
Matematică. M: Forum-Infa 2008.
Fișe individuale cu opțiune practică de lucru.
1. Material teoretic și exemple de găsire a derivatei unei funcții.
Definiție: Derivata funcției f(x) (f"(x)) la punctul x este limita raportului dintre incrementul funcției și incrementul argumentului atunci când incrementul argumentului tinde spre zero:
https://pandia.ru/text/78/405/images/image061_0.png" width="209 height=235" height="235">
Reguli de diferențiere.
Dacă funcțiile f(x) și g(x) au derivate, atunci
2. (u+v)′=u′+v′
3. (uv)′=u′v+v′u
4. (C u)′=C u′, unde C=const
5..png" width="49" height="54 src=">
6. Derivată a unei funcții complexe:
f′(g(x))=f′(g) g′(x)
2. Exemple.
1..png" width="61" height="41 src=">.png" width="20" height="41 src=">.png" width="20" height="41 src="> .png" width="69" height="41 src=">+4).
Funcția este produsul a doi factori: u=https://pandia.ru/text/78/405/images/image071_0.png" width="72" height="41 src=">.png" width=" 64" height="41 src=">.png" width="19" height="41 src=">.png" width="45" height="51 src=">.
Funcția este câtul a două expresii: u=https://pandia.ru/text/78/405/images/image079.png" width="52" height="41 src=">..png" width= "215" " height="57 src=">.png" width="197 height=36" height="36">
Soluţie. Să găsim derivata acestei funcții folosind regula de diferențiere a funcțiilor complexe (formula 6):

5. Dacă , atunci 
6. y = X 3 – 3X 2 + 5X+ 2. Să găsim y "(–1).
y " = 3X 2 – 6X+ 5. Prin urmare, y "(–1) = 14.
7. Dacă y= jurnal X cos X, Acea y" = (ln X)"cos X+ln X(cos X) " =1/X∙cos X– ln X păcat X.
Să fie dată o funcție. Pentru a-l studia ai nevoie de:
1) Găsiți domeniul său de definiție. Dacă nu este prea dificil, este util să găsiți și intervalul. (Cu toate acestea, în multe cazuri, problema găsirii este amânată până când se găsesc extremele funcției.)
2) Aflați proprietățile generale ale funcției care vor ajuta la determinarea comportamentului acesteia: dacă funcția este pară sau impară, dacă este periodică.
3) Aflați cum se comportă funcția atunci când argumentul se apropie de punctele limită ale domeniului de definiție, dacă există astfel de puncte de limită. Dacă o funcție are puncte de discontinuitate, atunci aceste puncte ar trebui verificate și pentru prezența asimptotelor verticale ale funcției. Găsiți asimptote oblice.
4) Găsiți punctele de intersecție ale graficului cu axele de coordonate, care constă în simpla calculare a valorii funcției cu condiția:
Cu axa OX: y=0;
Cu axa OY: x=0.
Găsirea punctelor de intersecție cu axa poate duce la necesitatea rezolvării unei ecuații algebrice complexe, care, poate, se poate face doar aproximativ. După ce am găsit rădăcinile funcției și punctele de discontinuitate, putem determina semnul funcției la fiecare dintre intervalele dintre aceste puncte. Acest lucru se poate face fie prin calcularea valorii funcției în orice punct din interval, fie prin utilizarea metodei intervalului.
5) Găsiți intervale de monotonitate. Pentru a face acest lucru, găsiți derivata și rezolvați inegalitatea:
https://pandia.ru/text/78/405/images/image089.png" width="49" height="19 src=">, funcția este în scădere.
După ce am găsit intervalele de monotonitate, putem determina imediat punctele extremului local: unde o creștere este înlocuită cu o scădere, sunt situate maximele locale și unde o scădere este înlocuită cu o creștere, sunt situate minimele locale.
6) Găsirea intervalelor de convexitate și concavitate se realizează folosind derivata a doua..png" width="39" height="19 src="> pe intervalele:
dacă https://pandia.ru/text/78/405/images/image090.png" width="39" height="19 src=">‹0, atunci curba graficului funcției este convexă.
În același timp, definim punctele de inflexiune ca acele puncte în care funcția schimbă direcția de convexitate (și este continuă).
7) Aflarea punctelor de intersecție ale graficului cu asimptota și puncte suplimentare. Acest punct nu este obligatoriu, dar găsirea unor astfel de puncte face ca studiul funcției și al graficului acesteia să fie complet și complet.
Rețineți că este util să trasați imediat punctele pe axele de coordonate și pe graficul care sunt obținute în timpul studiului de funcții pe desen. Acest lucru ajută la înțelegerea aspectului graficului pe parcurs.
3. Fă-o singur:
|
opțiune | Aflați derivata funcției y: |
opțiune | Aflați derivata funcției y: |
1.y=6- | 1. y=-6- 5.y= |
||
1. y=-7-1 | 1. y=-7-1 |
||
1.y=4x-3tgx+6x-8 | 1.y=-5x+2ctgx+3x-2 |
||
Obiectivele lecției:
Educational- cunoaște formule de diferențiere; reguli de diferențiere;
diferențierea unei funcții complexe; sensul fizic și geometric al derivatului;
ecuația tangentei la graficul unei funcții.
Dezvoltare - să poată găsi derivate ale funcțiilor; rezolva probleme folosind sensul fizic, sensul geometric; aflați valoarea derivatei unei funcții într-un punct; explică şi justifică matematic corect acţiunile efectuate.
Educational - cultiva independența, responsabilitatea, reflecția.
În timpul orelor
I. Moment organizatoric.
II. Verificarea temelor
(în pauze, consultanții verifică (studenții) și atribuie note).
III. Stabilirea obiectivelor și motivația
Profesorul informează elevii că această lecție este ultima lecție pe tema „Calculul derivatelor” și îi invită să își formuleze propriile obiective.
Profesor: „Marele filozof Confucius a spus odată: „Trei căi duc la cunoaștere: calea reflecției este calea cea mai nobilă, calea imitației este calea cea mai ușoară și calea experienței este calea cea mai amară”. Așa că astăzi, la clasă, fiecare dintre voi va stabili pe ce cale de cunoaștere a acestui subiect se află.”
Elevii au sarcina de a-și demonstra cunoștințele și abilitățile în calcularea derivatelor și li se oferă un plan de lecție.
Etapa I: Finalizarea sarcinii folosind cardul „Remember”.
(testarea cunoștințelor de formule și reguli de diferențiere).
Etapa II: Lucrare frontală orală de repetare și generalizare a cunoștințelor.
Etapa a III-a:„Prognoza de testare” (la îndeplinirea acestei sarcini, ajutorul consultanților este acceptabil).
euEtapa a V-a: Rezolvarea unei probleme practice.
Etapa a V-a: Muncă independentă
Se evaluează etapele I, III, V de muncă și teme. Consultanții verifică și introduc rezultatele în tabelul de evaluare.
Criteriu de evaluare: "5"- 19-20 puncte;
"4"- 15-18 puncte;
"3"- 10-14 puncte.
Căi către cunoaștere
- Reproducerea și corectarea cunoștințelor de referință
Etapa I.
Ţintă: controlul, autocontrolul cunoașterii formulelor și regulilor de diferențiere
Tine minte! F.I. _________________________________________________ |
|
Derivat |
|
c,c - cons t |
|
|
|
|
|
f„(x)+ g"(X) |
|
f(X)* g(X) |
|
|
|
La sfârșitul acestei sarcini, se efectuează un autotest folosind „Tabelul derivatelor”. Cardurile sunt predate consultanților pentru verificare (corecțiile pe carduri nu sunt permise).
V. Generalizarea și sistematizarea cunoștințelor
Etapa II.
1. Lucru frontal oral.
A. Generați o sarcină pentru această condiție și rezolvați-o.
![]()
1. Aflați valoarea derivatei funcției în punctul t = 3. (Răspuns: 21.)
2. Creați o ecuație pentru tangenta la graficul funcției în punctul t = 3. (Răspuns: y = 21x-45.).
3. Aflați viteza corpului și accelerația în momentul t=3c, dacă legea mișcării este dată de formula. (Răspuns: 21 m/s, 16 m/s²).
4. Aflați coeficientul unghiular al tangentei trasate la graficul funcției în punctul t = 3. (Răspuns: 21.).
5. Aflați tangenta unghiului de înclinare al tangentei la graficul funcției în punctul t = 3 și determinați tipul unghiului dintre tangentă și direcția pozitivă a axei Ox. (Răspuns: tgα, unghiul α este acut)
B. Găsiți derivate ale funcțiilor

2. Etapa III„Prognoza de testare”


La finalul acestei sarcini, se efectuează un autotest pe baza răspunsurilor finale, iar testele sunt predate consultanților. (corecțiile pe carduri nu sunt permise).
Raspunsuri:
1 opțiune |
||||
Opțiunea 2 |
- Rezolvarea problemei
euEtapa V
Rezolvare frontală la o problemă de nivel avansat (soluția se realizează de către consultanți împreună cu clasa).
Sarcină
La ce valori ale parametrilor A tangente la graficul unei funcţii ![]()
desenate în punctele sale de intersecție cu axa X, formează între ele un unghi de 60°?

Graficul este o parabolă cu ramuri în sus care intersectează axa X în două puncte (cazul A=0 nu satisface sensul problemei):
IX. Rezumat și notare
1. Întrebări: a) A fost atins scopul lecției?
b) Care etapă mi s-a părut cea mai dificilă?
c) Care a fost cel mai interesant?
2. Consultanții anunță rezultatele (numărul și numele studenților pe drum
imitație, moduri de reflecție și moduri de experiență).
Lecție practică
Subiect: Găsirea derivatelor. Aplicarea derivatei la studiul funcțiilor și trasarea graficelor.
Ţintă: Stăpânește calculul derivatelor, învață să explorezi o funcție folosind derivata
Mijloace de educatie: caiete pentru exerciții practice, prezentări pe tema, resurse de pe internet.
1. Luați în considerare materialul teoretic pe subiectele: „Reguli pentru calcularea derivatelor”, „Extremul unei funcții”, „Convexitate, concavitate. Punct de inflexiune."
2. Examinați mostre de sarcini.
3. Finalizați sarcina de testare nr. 1.
Întrebări de control:
1. Definiți maximul (minimul) unei funcții într-un punct. Ce se poate spune despre semnul incrementului funcției într-o vecinătate destul de mică a punctului maxim (minim)?
2. Care sunt condițiile necesare pentru existența unui extremum al unei funcții? Care este semnificația lor geometrică?
3. Care este regula pentru a găsi cele mai mari și cele mai mici valori ale unei funcții pe un segment?
4. Definiți convexitatea (concavitatea) unei curbe pe un interval.
5. Care este regula pentru aflarea intervalelor de convexitate si concavitate ale unei curbe?
6. Punctul de inflexiune al curbei. Cum să o găsesc?
7. Care este algoritmul pentru construirea unui grafic al unei funcții?
Reguli pentru calcularea instrumentelor derivate
Derivată a unei funcții complexe.
Dacă la=ƒ( Și), u=φ(x), atunci la¢ ( X)=ƒ¢ (i)·φ¢ (X).
Derivată a unei sume.
Dacă la(X)=Și(X)+v (X), Acea la¢ (X)=Și¢ (X)+v ¢ (X)
Derivat al produsului.
Dacă y(x)=u(X)· v (X), Acea la¢ = Și¢ · v + u · v ¢ .
În special, ( Cu· Și)¢ =c· Și¢, adică factorul constant este scos de sub semnul derivatei. Este ușor să verifici asta
(u 2 ) ¢ = 2 u·u ¢ , (u 3 ) ¢ =3u 2 u ¢ , … , (u n ) ¢ =n·u n–1 u ¢ .
Derivată a coeficientului.
Daca atunci  .
.
Tabelul derivatelor
1. (Cu)¢ =0
Pentru o funcție complexă: dacă u=u(x), Acea:
2. (X)¢ =1
3. (X α )¢ = α · Xα–1, A– orice număr real.
 .
.
3. 

4. (A X ) ¢ =a X · ln A
4. 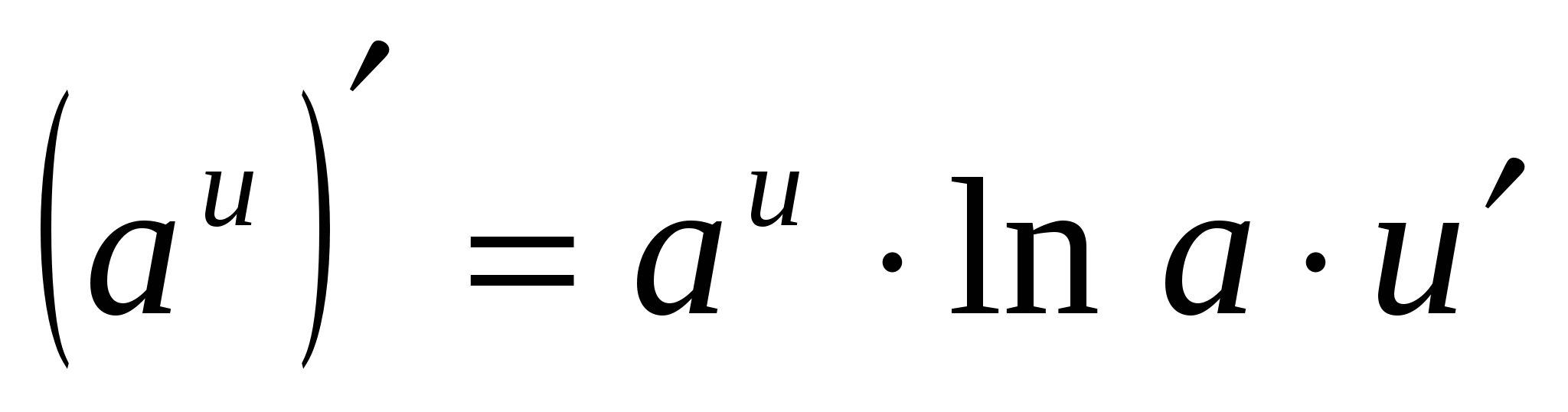

5. (Buturuga
A
X)
¢
=
 .
.
5. 

6. (păcat x)¢ =cos x
6. 
7. (cos x)¢ = –sin x
7. 
8. (tg x)¢
=
8. 
9. (ctg x)¢
=
9. 
10. 
10. 
11. 
11. 
12. 
12. 
13. 
13. 
Examinare exemple
Exemplul 1.
y=(3–2 sin 5x ) 4 | Aplicam formule derivate pentru Și α ,păcat u |
y ¢ =4·(3–2·sin5x) 3·(3–2sin5x) ¢ =4·(3–2·sin5x) 3 ·(0–2·cos5x·5) = –40·(3–2·sin5x) 3 .
Exemplul 2.
. 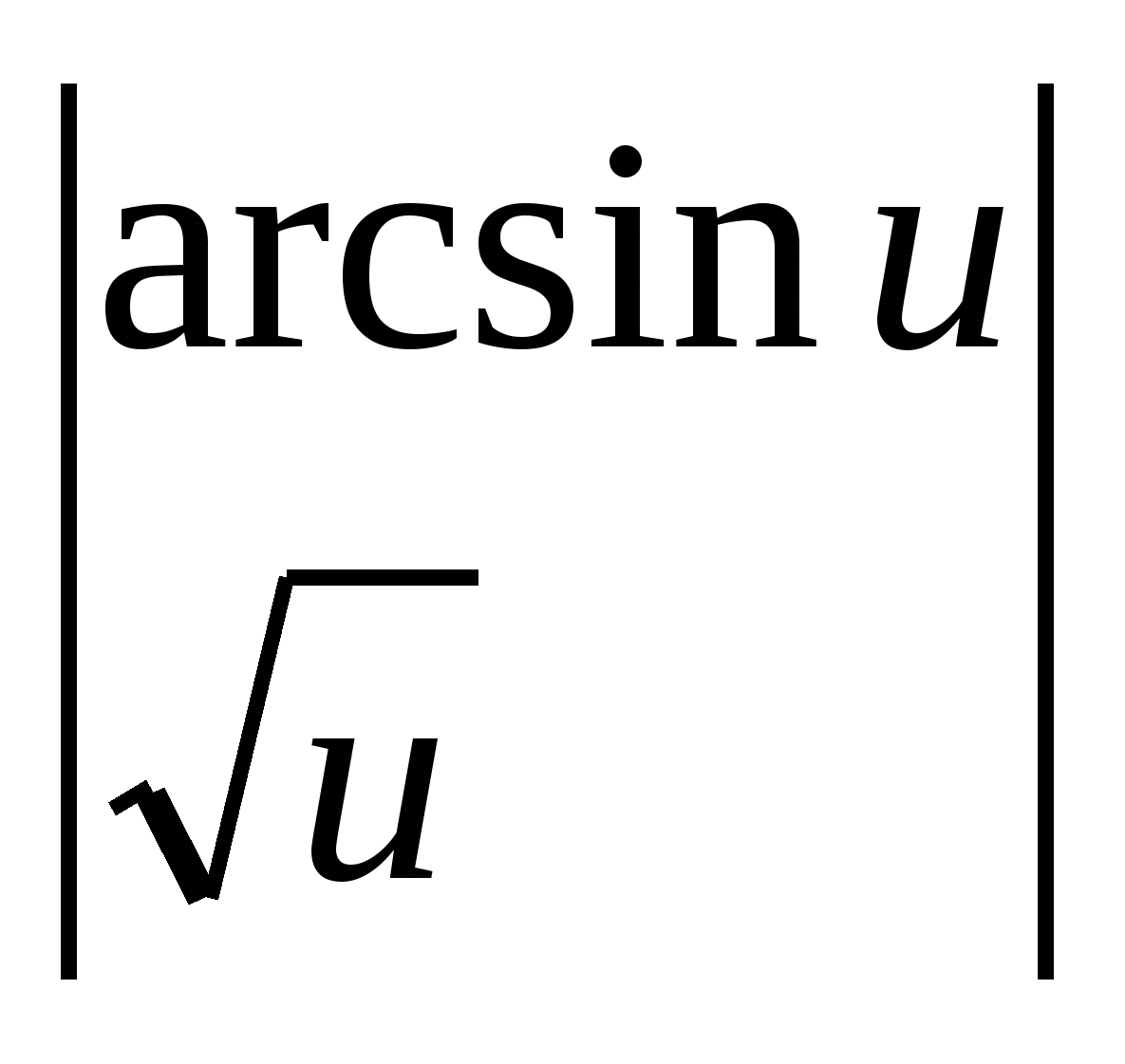

Exemplul 3.
 .
. 

Exemplul 4.



Exemplul 5.
 .
. 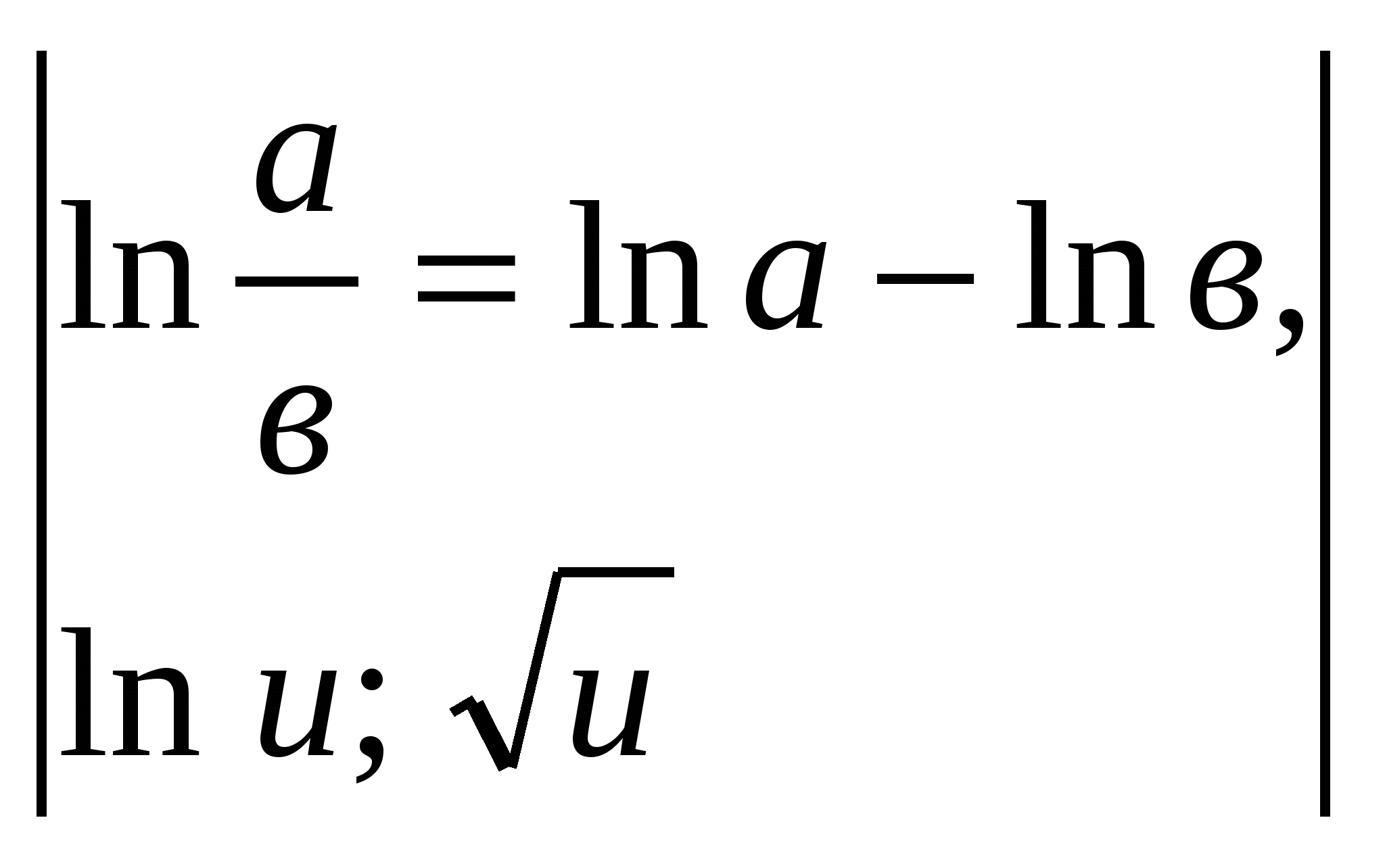

Extremul funcției
Studiul unei funcții la un extrem este una dintre cele mai importante aplicații ale derivatelor. Să ne uităm la definiția minimelor și maximelor și cum să le găsim.
Fie funcția ƒ( X) este definită și diferențiabilă pe o anumită mulțime și un punct X 0 este un punct în interiorul acestuia.
Definiție. Funcţie ƒ (X) la un moment dat X 0 are maxim(minimum), dacă există o astfel de vecinătate a punctului X 0, care este pentru toată lumea X din aceasta zona ƒ (X) < ƒ (X 0 ) (ƒ (X) > ƒ (X 0 )).
Punct X 0 se numește atunci punct maxim(minim).

Orez. 1.
Este prezentat un grafic al unei funcții care are două puncte maxime ( X 1 și X 3) și două puncte minime ( X 2 și X 4), iar valoarea maximă poate fi mai mică decât minimul ( ƒ (X 1 ) < ƒ (X 4)). Aceasta subliniază faptul că caracterizăm singularitatea unei funcții numai în apropierea unui anumit punct.
Valorile funcției în punctele de maxim și minim se numesc valori extreme sau extreme. Graficul de mai sus arată că punctele extreme ( X 1 , X 2 , X 3 , X 4) determinați intervalele de monotonitate ale funcției, în fiecare dintre care derivata păstrează un anumit semn. La punctele extreme, desigur, derivata merge la zero. Să formulăm o teoremă despre conditie necesara existența unui extremum.
Teorema. Dacă funcţia ƒ (X) la un moment dat X 0 are un extremum, atunci derivata funcției în acest punct este egală cu zero, adică ƒ¢ ( X 0)=0.
Să observăm imediat că această condiție nu este suficientă, adică afirmația inversă nu este întotdeauna adevărată. Din egalitate ƒ ¢ ( X 0)= 0 nu înseamnă neapărat că la punct X 0 există un extremum.
Acest lucru este confirmat de un exemplu cu funcția ƒ (X)=x 3 .
Vom găsi ƒ ¢ ( X)= 3X 2 . La punctul X=0 ƒ ¢ (0)=0 . Dar cât de aproape de subiect doriți X=0 vom găsi X> 0, unde ƒ (X)=x 3 > 0, vom găsi X< 0, где ¦ (X)=X 3 < 0. Т. е. не существует какая-либо малая окрестность точки X=0, unde pentru toate X valoarea funcției într-un punct X=0 va fi cel mai mare sau cel mai mic. Prin urmare punct X=0 nu este un punct extremum.
Se poate argumenta altfel. Din moment ce derivatul ƒ ¢ (x)=3x 2 , apoi funcția ƒ(x)=x 3 crește pentru orice x real și nu are extreme.
Puncte în care condiția extremum necesară este îndeplinită (ƒ ¢ (x)=0) sunt numite critic .
În mod evident, tangenta la graficul funcției în punctele în care ƒ ¢ (x)=0, paralel cu axa x Ox .
Stare suficientă extremul este dat în următoarele teoreme.
Teorema 1. Dacă X 0 este punctul critic al funcției și atunci când trece prin el derivata își schimbă semnul X 0 este un punct extremum, și anume, dacă derivata își schimbă semnul din plus în minus, este un punct maxim, iar dacă își schimbă semnul din minus în plus, este un punct minim.
Rețineți că nu există un extremum într-un punct dacă derivata nu își schimbă semnul. Regula pentru studierea extremumului folosind derivata întâi este cunoscută din cursul școlar. Uneori este mai convenabil să se formuleze o condiție suficientă pentru un extremum folosind derivata a doua.
Fie funcția ƒ( X) este de două ori diferențiabilă într-un anumit domeniu (adică ƒ( X) are ƒ¢ ( X) Și ƒ ¢¢ ( X)).
Teorema 2. Dacă X 0 – punctul critic al funcției ƒ(x)și ƒ ¢¢ (X 0 ) > 0 , Acea X 0 – punct minim, dacă ƒ ¢¢ (X 0 ) < 0, то X 0 – punct maxim.
Folosind derivata a doua, se determină convexitatea sau concavitatea graficului unei funcții.
Convexitate, concavitate. Punct de inflexiune.
Curba y=ƒ(X) se numește convexth de mai jos oricare dintre ei tangentă
ƒ ¢¢ ( X) < 0.
Curba y=ƒ(X) se numește concav pe un interval dacă toate punctele curbei se află superior oricare dintre ei tangentă pe acest interval. Apoi pe acest interval
ƒ ¢¢(x) > 0
Definiție. Punct de inflexiune o curbă este un punct în care curba este convexă pe o parte și concavă pe cealaltă.
La punctul de inflexiune ƒ ¢¢ ( X)=0.
Deci, semnul derivatei a doua (precum și semnul funcției în sine și derivata sa prima) indică caracteristicile graficului funcției. Să ne uităm din nou la ele.
Dacă pentru toată lumea X pe interval ( A, b) ƒ (X) > 0 (ƒ (X) < 0), atunci graficul se află deasupra (dedesubt) axei x.
Dacă pentru toată lumea X pe interval ( A, b) ƒ ¢ ( X) > 0 (ƒ ¢ ( X) < 0), то функция на (A, b) crește (descrește).
Dacă pentru toată lumea X pe interval ( A, b) ƒ ¢¢ ( X) > 0 (ƒ ¢¢ ( X) < 0), то график на (A, b) concav (convex).
Ecuația ƒ( X)=0 definește „zerurile” funcției, adică punctele de intersecție ale graficului cu axa Ox.
Ecuația ƒ ¢ ( X)=0 definește punctele critice.
Ecuația ƒ ¢¢ ( X)=0 definește posibilele puncte de inflexiune.
Schema de studiu a funcției
Pentru a studia funcția ƒ (X) și complot y=ƒ(X) ar trebui găsite:
1) domeniul de definire al funcției și punctul de intersecție a graficului cu axele de coordonate;
2) intervale de monotonie;
3) puncte de extremă și valori ale funcției în aceste puncte;
4) intervale de convexitate și concavitate ale graficului;
5) punctele de inflexiune ale graficului;
6) construiți într-un sistem de coordonate carteziene toate punctele obținute (uneori, pentru a clarifica graficul, se obțin puncte suplimentare) și graficul în sine.
Cele mai mici și cele mai mari valori ale unei funcții pe un segment
Atunci când rezolvați unele probleme ale metodei de optimizare, este important să puteți găsi cele mai mici sau mai mari valori ale unei funcții pe un anumit segment. Funcția atinge aceste valori fie în punctele critice, fie la capetele segmentului.
Schema de căutare cele mai mici și cele mai mari valori ale funcției ƒ (X) pe segmentul [ A, b].
1. Aflați derivata funcției ƒ ¢ ( X).
2. Aflați punctele critice din ecuație ƒ ¢ ( X)=0.
3. Selectați acele puncte critice care aparțin acestui segment [ A, b] și găsiți valoarea funcției ƒ (X) în fiecare astfel de punct.
4. Calculați valorile funcției ƒ (X) la capetele segmentului: ƒ( A) și ƒ( b).
5. Din valorile funcției obținute, selectați cel mai mare (cel mai mare) și cel mai mic (cel mai mic).
Exemplul 2.
Găsiți cele mai mari și cele mai mici valori ale unei funcții ƒ(x)=X 3 –9x 2 +24х–10 pe segment.
1. ƒ ¢ ( X)= 3X 2 – 9·2 X 2 + 24.
2. ƒ ¢ ( X)=0, 3(X 2 –6X+8)=0, X 1 =2, X 2 =4.
3. Punctul x 2 =4 nu aparține segmentului. Prin urmare, calculăm valoarea funcției numai la punctul X 1 =2
ƒ(2)=2 3 –9·2 2 +24·2–10=10.
4. Valorile funcției la capetele segmentului: ƒ(0)= –10, ƒ(3)=3 3 –9·3 2 +24·3–10, ƒ(3)=8.
5. Valori obținute:
ƒ(2)=10, ƒ(0)= –10, ƒ(3)=8.
Cea mai mare valoare este 10 și este atinsă în punctul respectiv X=2. Cel mai mic este egal cu –10 și se realizează la punctul X=0.
Exemplul 3.
Aflați intervalele de convexitate și concavitate și punctele de inflexiune ale curbei y=x+36X 2 –2X 3 –X 4 .
Domeniul de definire al acestei funcții este mulțimea tuturor numerelor reale, adică. XЄ(–∞, +∞).
Să găsim derivata a doua.
la¢ =1+72 X–6X 2 –4X 3 .
la¢¢ =72–12 X–12X 2 = –12(X 2 +X–6).
Din Ec. la¢¢ =0 obținem abscisa punctului de inflexiune:
–12(X 2 +X–6)=0 X 1 = –3; X 2 =2.
Să definim semnul la¢¢ pe intervale
(–∞; –3), (–3; 2), (2, +∞).
X
(–∞, –3)
(–3; 2)
(2; +∞)
la¢¢
forma curba
convex
inflexiune
concav
inflexiune
convex
Să găsim ordonatele punctelor de inflexiune:
la(–3)=726; M 1 (–3; 726) – punct de inflexiune
la(2)=114; M 2 (2; 114) – punct de inflexiune.
Pe intervalul (–3; 2) curba este concavă. Pe intervalele (–∞; –3) și (2; +∞) – convex.
Exemple de sarcini
Sarcina nr. 1.
Găsiți punctele de întrerupere ale funcției și trasați graficul

Funcţie ƒ (X) este definit pentru toate reale Xși este continuă pe fiecare dintre intervalele indicate: (–∞; –1), [–1; 0], (0, +∞). Să explorăm funcția ƒ (X) pentru continuitate în puncte X= –1 și X=0.
Pentru a face acest lucru, vom găsi limite unilaterale în fiecare dintre aceste puncte.

Din moment ce limitele unilaterale sunt diferite, atunci X = –1 – punct de discontinuitate de primul fel.

Limitele unilaterale sunt egale, adică în punctul x=0 există o limită a funcției și 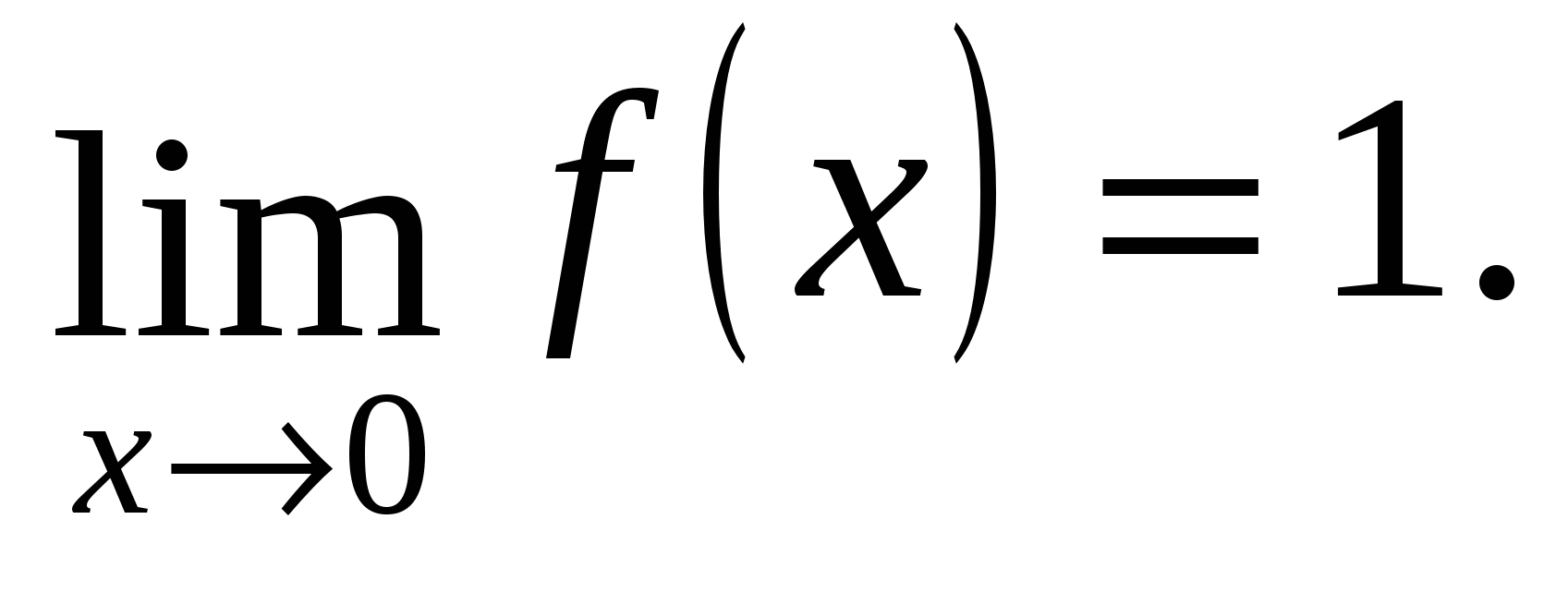
Să comparăm această limită cu valoarea funcției în punctul: 
Deoarece  apoi în la x=0 funcţia ƒ(x) este continuă.
apoi în la x=0 funcţia ƒ(x) este continuă.
Să reprezentăm grafic funcția ƒ (X), dat fiind
1)  - ecuația unei linii drepte,
- ecuația unei linii drepte,
2)  – ecuația semicercului superior
– ecuația semicercului superior  cu centrul la origine și raza egală cu unitatea și cu condiția –1 £ X 0 £ ecuație
cu centrul la origine și raza egală cu unitatea și cu condiția –1 £ X 0 £ ecuație  definește un sfert de cerc.
definește un sfert de cerc.
3) pentru X > 0 graficul este dat de ecuație  . Găsim punctele de intersecție ale acestei curbe cu axa Ox din ecuație
. Găsim punctele de intersecție ale acestei curbe cu axa Ox din ecuație  pentru x > 0. x= π
n, Unde n
=1, 2, 3, 4,
pentru x > 0. x= π
n, Unde n
=1, 2, 3, 4,

Orez. 2.
Sarcina nr. 2.
Scrieți ecuații pentru tangente la o dreaptă  în punctele în care X=0 și X=4. Aflați punctul de intersecție al tangentelor și unghiul dintre ele. Faceți un desen.
în punctele în care X=0 și X=4. Aflați punctul de intersecție al tangentelor și unghiul dintre ele. Faceți un desen.
Ecuația unei tangente la o dreaptă y=ƒ(x) se pare ca
Unde la 0 =ƒ( X 0).
La punctul X=0 la(0)=ƒ(0)=5.
la¢ =ƒ ¢ (X)=X–3 ƒ¢ (0)= –3.
M 1 (0, 5) are forma y– 5= –3(X–0) sau
y= –3X+5.
La punctul X=4 la(4)=ƒ(4)=1. ƒ¢ (4)=4–3=1.
Ecuația unei tangente la un punct M 2 (4, 1) are forma y– 1=X–4 sau
y=x–3.
Obținem punctul de intersecție al tangentelor prin rezolvarea sistemului

Punct de intersecție M 3 (2, –1).
Colţ φ între tangente găsim din formula:
 ,
,
Unde k 1 = –3; k 2 =1 – coeficienții unghiulari ai tangentelor.
 .
.
Colţ φ =arctg 2.
Să construim această linie  – o parabolă cu un vârf în punctul în care X=3, pentru că la¢
=0 la X=3. Vom găsi
– o parabolă cu un vârf în punctul în care X=3, pentru că la¢
=0 la X=3. Vom găsi  . Punct M 4 (3;
. Punct M 4 (3;  ) este vârful parabolei.
) este vârful parabolei.
R 
este. 3.
Sarcina nr. 3.
Explorați funcția  și complotează-l.
și complotează-l.
1. Această funcție este un polinom (puteți deschide parantezele, obținem un polinom de gradul trei), prin urmare este definită, continuă și diferențiabilă pentru orice X.
2. Să găsim derivata.
 .
.
Din Ec. la¢ =0 să găsim punctele critice: 3 X·( X–2)=0, X 1 =0, X 2 =2.
Să le explorăm.
X
(–∞, 0)
(0; 2)
(2; +∞)
la ¢
la
3. Deci, funcția crește pe intervalele (–∞, 0) și (2, +∞), scade pe intervalul (0; 2), are un maxim la x=0 și un minim la x=2:
la max = la(0)=4; la min = la(2)=0.
4. Să găsim derivata a doua.
la¢¢ = 6·( X-1).
Curba este convexă unde la¢¢ < 0, т. е. 6·(X–1) < 0, X < 1.
Curba este concavă unde la¢¢ > 0, adică X > 1.
Deci, pe intervalul (–∞, 1) curba este convexă; iar pe intervalul (1, +∞) este concav.
5. Găsim punctul de inflexiune din ecuație la¢¢ =0. Prin urmare, X=1 – abscisa punctului de inflexiune, deoarece acest punct separă intervalele de convexitate și concavitate ale curbei. ordonata punctului de inflexiune: la(1)=2.
Graficul unei funcții la=(X+1)·( X–2) 2 intersectează axa Ox la la=0, adică când X= –1 și X=2;
traversează axa Oy la X=0, adică când la=4. Am obținut trei puncte: (–1; 0), (2; 0), (0; 4). Vom introduce toate punctele obținute în tabel, adăugându-le pe cele adiacente.
–2
–1



–16


este. 4 Curba y=(x+1)(x–2) 2.
Sarcina nr. 1
Vă prezentăm sarcini care pot avea unul, două, trei sau mai multe răspunsuri corecte. Încercuiește numerele tuturor răspunsurilor corecte.
1. Dacă  apoi functia
apoi functia
1) în creștere
2) în scădere
3) constantă
2. Dacă
1) În creștere
2) În scădere
3. Dacă  , apoi funcția
, apoi funcția
1) În creștere
2) În scădere
4. Dacă  , apoi funcția
, apoi funcția
1) Crescătoare 3) Descrescătoare
2) Constant 4) Monoton
5. Funcție  Este
Este
1) Chiar și
2) Nici măcar
3) nici par, nici impar
4) Periodic
5) Nu periodic
6) Trigonometric
7) Elementare
6. Funcția  Este
Este
1) chiar
2) ciudat
3) nici par, nici impar
4) periodic
5) nu periodic
6) trigonometric
7) elementar
2) Weierstrass 4) Dirichlet 6) Leibniz
8) Rezolvare  Ecuații
Ecuații
1) 0 3) 0 și 3 5) 2 7) 3
2) 2 și 3 4) 2 6) -5 și 1 8) 5 și 1
9) soluția inegalității 
1) ( ; 1) 3) (
; 1) 3) ( ; 1) 5) (-
; 1) 5) (- ;1)
;1)
2) (1; 5) 4) (2;  ) 6)
) 6) 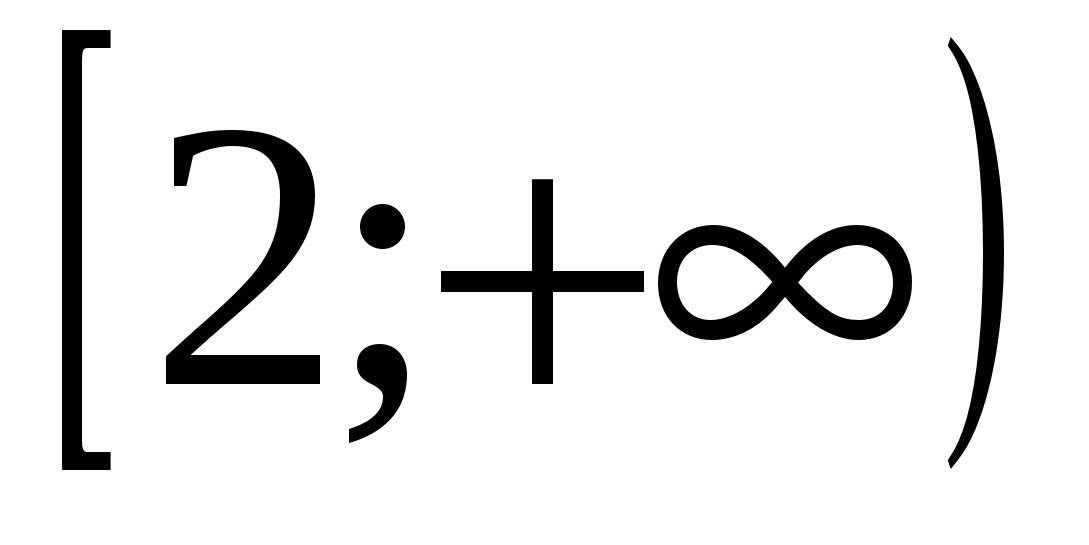
10) Metoda  Se găsește suma
Se găsește suma
1) vectori
2) drept
3) segment
11) Dacă  , apoi funcția
, apoi funcția
1) Concav 3) Convex 5) Descrescător
2) Monoton 4) Crescător 6) Constant
12) domeniul de definire al funcției este egal cu 
1) ( ;0)
;0)
2) (0;  )
)
3) (- ;
; )
)
4) (0;1)
5) 
6) 
7) (-1;1)
8) 
9) 
13) funcția  este
este
1) indicativ
2) trigonometric
3) putere
4) logaritmică
14) dacă funcţiile y = X  atunci ea este
atunci ea este 
1) chiar
2) ciudat
3) nici par, nici impar
15) funcția  la
la  este
este

 .
.



