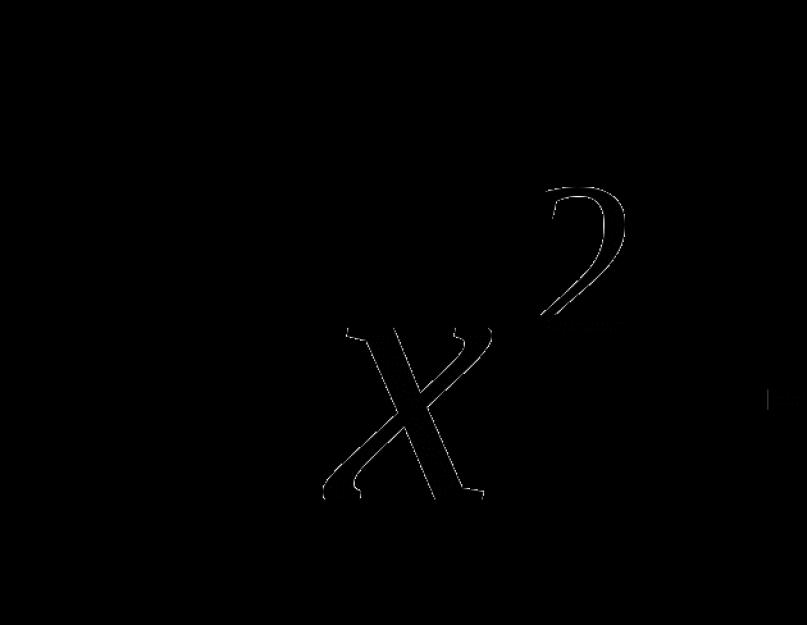Rezumatul lecției

„Metode de rezolvare ecuații iraționale»

Profil fizica si matematica clasa a XI-a.

Zelenodolsky districtul municipal RT"

Valieva S.Z.

Tema lecției: Metode de rezolvare a ecuațiilor iraționale

Obiectivul lecției: 1.Explorați diverse moduri rezolvarea ecuațiilor iraționale.

1. 
   Dezvoltați capacitatea de generalizare, selectare corectă a metodelor de rezolvare a ecuațiilor iraționale.
2. 
   Dezvoltați independența, îmbunătățiți alfabetizarea vorbirii

Tip de lecție: seminar.
Planul lecției:

1. 
   Moment organizatoric
2. 
   Învățarea de materiale noi
3. 
   Consolidare
4. 
   Teme pentru acasă
5. 
   Rezumatul lecției

Progresul lecției
eu. Moment organizatoric: mesajul subiectului lecției, scopul lecției.

În lecția anterioară, ne-am uitat la rezolvarea ecuațiilor iraționale care conțin rădăcini pătrate prin pătrarea acestora. În acest caz, obținem o ecuație corolară, care uneori duce la apariția rădăcinilor străine. Și apoi o parte obligatorie a rezolvării ecuației este verificarea rădăcinilor. De asemenea, ne-am uitat la rezolvarea ecuațiilor folosind definiția rădăcinilor pătrate. În acest caz, verificarea poate să nu fie efectuată. Cu toate acestea, atunci când rezolvați ecuații, nu ar trebui să începeți întotdeauna imediat să aplici „orbește” algoritmi pentru rezolvarea ecuației. În sarcinile Examenului de stat unificat există destul de multe ecuații, la rezolvarea cărora este necesar să alegeți o metodă de rezolvare care vă permite să rezolvați mai ușor și mai rapid ecuațiile. Prin urmare, este necesar să cunoaștem și alte metode de rezolvare a ecuațiilor iraționale, cu care ne vom familiariza astăzi. Anterior, clasa a fost împărțită în 8 grupuri creative și li s-au oferit exemple specifice pentru a dezvălui esența unei anumite metode. Le dăm cuvântul.

II. Învățarea de materiale noi.

Din fiecare grupă, 1 elev explică copiilor cum să rezolve ecuații iraționale. Întreaga clasă ascultă și ia notițe despre povestea lor.

1 cale. Introducerea unei noi variabile.

Rezolvați ecuația: (2x + 3) 2 - 3

4x 2 + 12x + 9 - 3

4x 2 - 8x - 51 - 3

, t ≥0

x 2 – 2x – 6 = t 2;

4t 2 – 3t – 27 = 0

x 2 – 2x – 15 =0

x 2 – 2x – 6 =9;

Răspuns: -3; 5.

Metoda 2. cercetare DL.

Rezolvați ecuația

ODZ:


x = 2. Prin verificare suntem convinși că x = 2 este rădăcina ecuației.

3 căi. Înmulțirea ambelor părți ale ecuației cu factorul conjugat.

+
(înmulțiți ambele părți cu -
)

x + 3 – x – 8 = 5(-)

2=4, deci x=1. Prin verificare suntem convinși că x = 1 este rădăcina acestei ecuații.

4 moduri. Reducerea unei ecuații la un sistem prin introducerea unei variabile.

Rezolvați ecuația

Fie = u,
=v.

Obținem sistemul:

Să rezolvăm prin metoda substituției. Obținem u = 2, v = 2. Aceasta înseamnă

obținem x = 1.

Răspuns: x = 1.

5 moduri. Selectarea unui pătrat complet.

Rezolvați ecuația

Să extindem modulele. Deoarece -1≤сos0.5x≤1, apoi -4≤сos0.5x-3≤-2, ceea ce înseamnă . De asemenea,

Apoi obținem ecuația

x = 4πn, nZ.

Răspuns: 4πn, nZ.

6 moduri. Metoda de evaluare

Rezolvați ecuația

ODZ: x 3 - 2x 2 - 4x + 8 ≥ 0, prin definiție partea dreaptă este -x 3 + 2x 2 + 4x - 8 ≥ 0

primim
aceste. x 3 - 2x 2 - 4x + 8 = 0. Rezolvând ecuația prin factorizare, obținem x = 2, x = -2

Metoda 7: Utilizarea proprietăților de monotonitate a funcțiilor.

Rezolvați ecuația. Funcțiile cresc strict. Suma funcțiilor crescătoare este în creștere și această ecuație are cel mult o rădăcină. Prin selecție găsim x = 1.

8 moduri. Folosind vectori.

Rezolvați ecuația. ODZ: -1≤х≤3.

Fie vectorul
. Produs punctual vectori - da partea stângă. Să găsim produsul lungimii lor. Aceasta este partea dreaptă. Primit
, adică vectorii a și b sunt coliniari. De aici
. Să pătram ambele părți. Rezolvând ecuația, obținem x = 1 și x =
.

1. 
   Consolidare.(fiecărui elev i se oferă fișe de lucru)

Lucru oral frontal

Găsiți o idee pentru rezolvarea ecuațiilor (1-10)

1.
(ODZ - )

2.
x = 2

3. x 2 – 3x +
(înlocuire)

4. (selectarea unui pătrat complet)

5.
(Reducerea unei ecuații la un sistem prin introducerea unei variabile.)

6.
(înmulțirea cu expresia conjugată)

7.
deoarece
. Atunci această ecuație nu are rădăcini.

8. Pentru că Fiecare termen este nenegativ, îi echivalăm cu zero și rezolvăm sistemul.

9. 3

10. Aflați rădăcina ecuației (sau produsul rădăcinilor, dacă sunt mai multe) ecuației.

Scris munca independenta urmată de verificare

rezolva ecuațiile numerotate 11,13,17,19

Rezolvarea ecuațiilor:

12. (x + 6) 2 -

14.

Metoda de evaluare

Utilizarea proprietăților de monotonitate a funcțiilor.

Folosind vectori.

1. 
   Care dintre aceste metode sunt folosite pentru a rezolva alte tipuri de ecuații?
2. 
   Care dintre aceste metode ți-a plăcut cel mai mult și de ce?

1. 
   Temă pentru acasă: Rezolvați ecuațiile rămase.

Referinte:

1. 
   Algebra și începuturile analizei matematice: manual. pentru clasa a XI-a educatie generala instituții / S.M.Nikolsky, M.K.Potapov, N.N.Reshetnikov, A.V.Shevkin. M: Prsveshchenie, 2009

1. 
   Materiale didactice despre algebră și începuturile analizei pentru clasa a 11-a / B.M. Ivlev, S.M. Sahakyan, S.I. Schwartzburd. – M.: Educație, 2003.
2. 
   Mordkovich A. G. Algebra și începuturile analizei. Clasele 10 – 11: Cartea de probleme pentru învățământul general. instituţiilor. – M.: Mnemosyne, 2000.
3. 
   Ershova A. P., Goloborodko V. V. Independent și teste despre algebră și analiză de bază pentru clasele 10-11. – M.: Ilexa, 2004
4. 
   Examenul de stat unificat KIM 2002 - 2010

6. Simulator algebric. A.G.Merzlyak, V.B.Polonsky, M.S. Yakir. Un manual pentru școlari și solicitanți. Moscova: „Ilexa” 2001.
7. Ecuații și inegalități. Metode de rezolvare nestandard. educațional – manual metodologic. 10 – 11 clase. S.N. Oleinik, M.K. Potapov, P.I. Pasichenko. Moscova. "Dropie". 2001

Menținerea confidențialității dvs. este importantă pentru noi. Din acest motiv, am dezvoltat o Politică de confidențialitate care descrie modul în care folosim și stocăm informațiile dumneavoastră. Vă rugăm să examinați practicile noastre de confidențialitate și să ne comunicați dacă aveți întrebări.

Colectarea și utilizarea informațiilor personale

Informațiile personale se referă la date care pot fi folosite pentru a identifica sau contacta o anumită persoană.

Vi se poate cere să furnizați informațiile dumneavoastră personale în orice moment când ne contactați.

Mai jos sunt câteva exemple de tipuri de informații personale pe care le putem colecta și cum putem folosi aceste informații.

Ce informații personale colectăm:

• Când trimiteți o solicitare pe site, este posibil să colectăm diverse informații, inclusiv numele, numărul de telefon, adresa dumneavoastră e-mail etc.

Cum folosim informațiile dumneavoastră personale:

• Informațiile personale pe care le colectăm ne permit să vă contactăm cu oferte unice, promoții și alte evenimente și evenimente viitoare.
• Din când în când, putem folosi informațiile dumneavoastră personale pentru a trimite notificări și comunicări importante.
• De asemenea, putem folosi informații personale în scopuri interne, cum ar fi efectuarea de audituri, analize de date și diverse cercetări pentru a îmbunătăți serviciile pe care le oferim și pentru a vă oferi recomandări cu privire la serviciile noastre.
• Dacă participați la o tragere la sorți, la un concurs sau la o promoție similară, este posibil să folosim informațiile pe care le furnizați pentru a administra astfel de programe.

Dezvăluirea informațiilor către terți

Nu dezvăluim informațiile primite de la dumneavoastră către terți.

Excepții:

• Daca este necesar, in conditiile legii, procedura judiciara, în proceduri judiciare și/sau în baza unor anchete publice sau solicitări de la agentii guvernamentale pe teritoriul Federației Ruse - dezvăluie informațiile tale personale. De asemenea, putem dezvălui informații despre dumneavoastră dacă stabilim că o astfel de dezvăluire este necesară sau adecvată pentru securitate, aplicarea legii sau alte scopuri de importanță publică.
• În cazul unei reorganizări, fuziuni sau vânzări, este posibil să transferăm informațiile personale pe care le colectăm terței părți succesoare aplicabile.

Protecția informațiilor personale

Luăm măsuri de precauție - inclusiv administrative, tehnice și fizice - pentru a vă proteja informațiile personale împotriva pierderii, furtului și utilizării greșite, precum și împotriva accesului, dezvăluirii, modificării și distrugerii neautorizate.

Respectarea vieții private la nivelul companiei

Pentru a ne asigura că informațiile dumneavoastră personale sunt în siguranță, comunicăm angajaților noștri standarde de confidențialitate și securitate și aplicăm strict practicile de confidențialitate.

Rezolvarea ecuațiilor iraționale.

În acest articol vom vorbi despre soluții cele mai simple ecuații iraționale.

Ecuație irațională este o ecuație care conține o necunoscută sub semnul rădăcinii.

Să ne uităm la două tipuri ecuații iraționale, care sunt foarte asemănătoare la prima vedere, dar în esență sunt foarte diferite unele de altele.

(1)

(2)

În prima ecuație vedem că necunoscutul se află sub semnul rădăcinii gradului al treilea. Putem lua rădăcina ciudată a număr negativ, prin urmare, în această ecuație nu există restricții nici asupra expresiei de sub semnul rădăcinii, nici asupra expresiei din partea dreaptă a ecuației. Putem ridica ambele părți ale ecuației la a treia putere pentru a scăpa de rădăcină. Obținem o ecuație echivalentă:

Când ridicăm părțile din dreapta și din stânga ecuației la o putere impară, nu ne putem teme să obținem rădăcini străine.

Exemplul 1. Să rezolvăm ecuația

Să ridicăm ambele părți ale ecuației la a treia putere. Obținem o ecuație echivalentă:

Să mutăm toți termenii într-o parte și să punem x din paranteze:

Echivalând fiecare factor cu zero, obținem:

Răspuns: (0;1;2)

Să ne uităm îndeaproape la a doua ecuație: . În partea stângă a ecuației se află rădăcina pătrată, care ia doar valori nenegative. Prin urmare, pentru ca ecuația să aibă soluții, și partea dreaptă trebuie să fie nenegativă. Prin urmare, condiția este impusă în partea dreaptă a ecuației:

Titlu="g(x)>=0"> - это !} condiție pentru existența rădăcinilor.

Pentru a rezolva o ecuație de acest tip, trebuie să pătrați ambele părți ale ecuației:

(3)

Pătrarea poate duce la apariția rădăcinilor străine, așa că avem nevoie de ecuațiile:

Titlu="f(x)>=0"> (4)!}

Totuși, inegalitatea (4) rezultă din condiția (3): dacă partea dreaptă a egalității conține pătratul unei expresii, iar pătratul oricărei expresii poate lua numai valori nenegative, de aceea și partea stângă trebuie să fie non- negativ. Prin urmare, condiția (4) decurge automat din condiția (3) și a noastră ecuaţie este echivalent cu sistemul:

Title="delim(lbrace)(matrice(2)(1)((f(x)=g^2((x))) (g(x)>=0) ))( )">!}

Exemplul 2. Să rezolvăm ecuația:

.

Să trecem la un sistem echivalent:

Titlu="delim(lbrace)(matrice(2)(1)((2x^2-7x+5=((1-x))^2) (1-x>=0) ))( )">!}

Să rezolvăm prima ecuație a sistemului și să verificăm care rădăcini satisfac inegalitatea.

Inequality title="1-x>=0">удовлетворяет только корень !}

Răspuns: x=1

Atenţie! Dacă în procesul de rezolvare pătram ambele părți ale ecuației, atunci trebuie să ne amintim că pot apărea rădăcini străine. Prin urmare, fie trebuie să treceți la un sistem echivalent, fie la sfârșitul soluției, FACEȚI O VERIFICARE: găsiți rădăcinile și înlocuiți-le în ecuația originală.

Exemplul 3. Să rezolvăm ecuația:

Pentru a rezolva această ecuație, trebuie de asemenea să pătram ambele părți. Să nu ne deranjam cu ODZ și cu condiția existenței rădăcinilor în această ecuație, ci pur și simplu facem o verificare la sfârșitul soluției.

Să pătram ambele părți ale ecuației:

În timp ce studiază algebra, școlarii se confruntă cu multe tipuri de ecuații. Printre cele mai simple sunt cele liniare, care conțin o necunoscută. Dacă o variabilă dintr-o expresie matematică este ridicată la o anumită putere, atunci ecuația se numește pătratică, cubică, biquadratică și așa mai departe. Aceste expresii pot conține numere raționale. Dar există și ecuații iraționale. Ele diferă de altele prin prezența unei funcții în care necunoscutul se află sub semnul radical (adică pur extern, variabila aici poate fi văzută scrisă sub rădăcina pătrată). Rezolvarea ecuațiilor iraționale are propriile sale trăsături caracteristice. Atunci când se calculează valoarea unei variabile pentru a obține răspunsul corect, acestea trebuie luate în considerare.

„Nespus în cuvinte”

Nu este un secret pentru nimeni că matematicienii antici operau în principal cu numere raționale. Acestea includ, după cum se știe, numere întregi exprimate prin fracții periodice ordinare și zecimale, reprezentanți ai unei comunități date. Cu toate acestea, oamenii de știință din Orientul Mijlociu și Apropiat, precum și din India, care dezvoltă trigonometria, astronomia și algebra, au învățat și ei să rezolve ecuații iraționale. De exemplu, grecii cunoșteau cantități similare, dar punându-le sub formă verbală, au folosit conceptul „alogos”, care însemna „inexprimabil”. Ceva mai târziu, europenii, imitându-i, au numit astfel de numere „surde”. Ele diferă de toate celelalte prin aceea că pot fi reprezentate doar sub forma unei fracții neperiodice infinite, a cărei expresie numerică finală este pur și simplu imposibil de obținut. Prin urmare, mai des, astfel de reprezentanți ai regatului numerelor sunt scriși sub formă de numere și semne ca o expresie situată sub rădăcina celui de-al doilea sau într-o măsură mai mare.

Pe baza celor de mai sus, să încercăm să definim o ecuație irațională. Astfel de expresii conțin așa-numitele „numere inexprimabile”, scrise folosind semnul rădăcinii pătrate. Ele pot reprezenta tot felul de opțiuni destul de complexe, dar în lor în forma sa cea mai simplă Arata ca cel din fotografia de mai jos.

Când începeți să rezolvați ecuații iraționale, în primul rând trebuie să calculați aria valori acceptabile variabilă.

Are sens expresia?

Necesitatea verificării valorilor obținute decurge din proprietăți După cum se știe, o astfel de expresie este acceptabilă și are orice semnificație numai în anumite condiții. În cazul rădăcinilor de grade pare, toate expresiile radicale trebuie să fie pozitive sau egale cu zero. Dacă această condiție nu este îndeplinită, atunci notația matematică prezentată nu poate fi considerată semnificativă.

Să dăm un exemplu specific despre cum să rezolvăm ecuațiile iraționale (imaginea de mai jos).

ÎN în acest caz, Este evident că condițiile specificate nu pot fi îndeplinite pentru nicio valoare acceptată de valoarea dorită, deoarece se dovedește că 11 ≤ x ≤ 4. Aceasta înseamnă că numai Ø poate fi o soluție.

Metoda de analiză

Din cele de mai sus, devine clar cum se rezolvă anumite tipuri de ecuații iraționale. Aici într-un mod eficient Poate fi o simplă analiză.

Să dăm o serie de exemple care vor demonstra din nou clar acest lucru (imaginea de mai jos).

În primul caz, la o examinare atentă a expresiei, se dovedește imediat a fi extrem de clar că nu poate fi adevărată. Într-adevăr, partea stângă a egalității ar trebui să rezulte într-un număr pozitiv, care nu poate fi egal cu -1.

În al doilea caz, suma a două expresii pozitive poate fi considerată egală cu zero numai atunci când x - 3 = 0 și x + 3 = 0 în același timp. Și acest lucru este din nou imposibil. Și asta înseamnă că răspunsul ar trebui să fie din nou scris Ø.

Al treilea exemplu este foarte asemănător cu cel deja discutat mai devreme. Într-adevăr, aici condițiile ODZ cer ca următoarea inegalitate absurdă să fie îndeplinită: 5 ≤ x ≤ 2. Și o astfel de ecuație în același mod nu poate avea soluții sensibile.

Zoom nelimitat

Natura iraționalului poate fi explicată și cunoscută cel mai clar și complet doar prin seria nesfârșită de numere zecimale. Și specific, un exemplu strălucitor unul dintre membrii acestei familii este πi. Nu fără motiv, această constantă matematică este cunoscută încă din cele mai vechi timpuri, fiind folosită la calcularea circumferinței și a ariei unui cerc. Dar printre europeni a fost pusă în practică pentru prima dată de englezul William Jones și de elvețianul Leonard Euler.

Această constantă apare după cum urmează. Dacă comparăm cercuri cu circumferințe diferite, atunci raportul dintre lungimile și diametrele lor este în mod necesar egal cu același număr. Acesta este pi. Dacă o exprimăm printr-o fracție obișnuită, obținem aproximativ 22/7. Acest lucru a fost făcut mai întâi de marele Arhimede, al cărui portret este prezentat în figura de mai sus. De aceea un astfel de număr și-a primit numele. Dar aceasta nu este o valoare explicită, ci o valoare aproximativă a poate cel mai uimitor dintre numere. Un om de știință strălucit a găsit valoarea dorită cu o precizie de 0,02, dar, de fapt, această constantă nu are o semnificație reală, ci este exprimată ca 3,1415926535... Este o serie nesfârșită de numere, care se apropie la infinit de o valoare mitică.

Pătrare

Dar să revenim la ecuațiile iraționale. Pentru a găsi necunoscutul, în acest caz recurg foarte des metoda simpla: pătratează ambele părți ale egalității existente. Această metodă dă de obicei rezultate bune. Dar ar trebui să ținem cont de insidiosul cantităților iraționale. Toate rădăcinile obținute ca urmare a acestui fapt trebuie verificate, deoarece pot să nu fie potrivite.

Dar să continuăm să ne uităm la exemple și să încercăm să găsim variabilele folosind metoda nou propusă.

Nu este deloc dificil, folosind teorema lui Vieta, să găsim valorile dorite ale mărimilor după ce, în urma unor operații, ne-am format ecuație pătratică. Aici se dovedește că printre rădăcini vor fi 2 și -19. Cu toate acestea, când verificați, înlocuind valorile rezultate în expresia originală, vă puteți asigura că niciuna dintre aceste rădăcini nu este potrivită. Aceasta este o apariție comună în ecuațiile iraționale. Aceasta înseamnă că dilema noastră din nou nu are soluții, iar răspunsul ar trebui să indice un set gol.

Exemple mai complexe

În unele cazuri, este necesar să pătrați ambele părți ale unei expresii nu o dată, ci de mai multe ori. Să ne uităm la exemple în care acest lucru este necesar. Ele pot fi văzute mai jos.

După ce ați primit rădăcinile, nu uitați să le verificați, deoarece pot apărea altele suplimentare. Ar trebui explicat de ce este posibil acest lucru. Când se aplică această metodă, ecuația este oarecum raționalizată. Dar scăpând de rădăcinile care nu ne plac, care ne împiedică să efectuăm operații aritmetice, se pare că extindem gama existentă de semnificații, care este încărcată (după cum se poate înțelege) cu consecințe. Anticipând acest lucru, efectuăm o verificare. În acest caz, există șansa de a vă asigura că numai una dintre rădăcini este potrivită: x = 0.

Sisteme

Ce ar trebui să facem în cazurile în care trebuie să rezolvăm sisteme de ecuații iraționale și avem nu una, ci două necunoscute? Aici acționăm în același mod ca în cazurile obișnuite, dar ținând cont de proprietățile de mai sus ale acestor expresii matematice. Și în fiecare sarcină nouă, desigur, ar trebui să utilizați o abordare creativă. Dar, din nou, este mai bine să luați în considerare totul exemplu concret prezentat mai jos. Aici nu trebuie doar să găsiți variabilele x și y, ci și să indicați suma lor în răspuns. Deci, există un sistem care conține cantități iraționale (vezi fotografia de mai jos).

După cum puteți vedea, o astfel de sarcină nu reprezintă nimic supranatural de dificil. Trebuie doar să fii inteligent și să ghiciți că partea stângă a primei ecuații este pătratul sumei. Sarcini similare se găsesc în examenul de stat unificat.

Irațional în matematică

De fiecare dată, nevoia de a crea noi tipuri de numere a apărut în rândul umanității atunci când nu avea suficient „spațiu” pentru a rezolva unele ecuații. Numerele iraționale nu fac excepție. După cum mărturisesc fapte din istorie, marii înțelepți au acordat pentru prima dată atenție acestui lucru chiar înainte de epoca noastră, în secolul al VII-lea. Acest lucru a fost făcut de un matematician din India cunoscut sub numele de Manava. El a înțeles clar că este imposibil să extragi o rădăcină din unele numere naturale. De exemplu, acestea includ 2; 17 sau 61, precum și multe altele.

Unul dintre pitagoreeni, un gânditor pe nume Hippasus, a ajuns la aceeași concluzie încercând să facă calcule folosind expresii numerice ale laturilor pentagramei. După ce a descoperit elemente matematice care nu pot fi exprimate în valori numerice și nu au proprietățile numerelor obișnuite, și-a înfuriat atât de tare colegii încât a fost aruncat peste bord, în mare. Faptul este că alți pitagoreici au considerat raționamentul său o rebeliune împotriva legilor universului.

Semnul radicalului: evoluția

Semnul rădăcinii pentru exprimarea valorii numerice a numerelor „surde” nu a început imediat să fie utilizat în rezolvarea inegalităților și ecuațiilor iraționale. Matematicienii europeni, în special italieni, au început să se gândească la radical în jurul secolului al XIII-lea. În același timp, le-a venit ideea de a folosi R latin pentru desemnare, dar matematicienii germani au acționat diferit în lucrările lor. Le-a plăcut mai mult litera V În Germania, denumirea V(2), V(3) s-a răspândit în curând, care era menită să exprime rădăcina pătrată a lui 2, 3 și așa mai departe. Mai târziu, olandezii au intervenit și au modificat semnul radicalului. Iar Rene Descartes a completat evoluția, aducând semnul rădăcinii pătrate la perfecțiunea modernă.

A scăpa de irațional

Ecuațiile și inegalitățile iraționale pot include o variabilă nu numai sub semnul rădăcinii pătrate. Poate fi de orice grad. Cea mai obișnuită modalitate de a scăpa de el este ridicarea ambelor părți ale ecuației la puterea corespunzătoare. Aceasta este acțiunea principală care ajută la operațiunile cu iraționalul. Acțiunile din cazurile pare nu sunt deosebit de diferite de cele despre care am discutat deja mai devreme. Aici trebuie luate în considerare condițiile de non-negativitate a expresiei radicalului, iar la sfârșitul soluției este necesar să se filtreze valorile străine ale variabilelor în același mod cum a fost arătat în exemplele deja luate în considerare. .

Printre transformările suplimentare care ajută la găsirea răspunsului corect, se folosește adesea înmulțirea expresiei cu conjugatul său și este deseori necesară introducerea unei noi variabile, care facilitează rezolvarea. În unele cazuri, este recomandabil să folosiți grafice pentru a găsi valoarea necunoscutelor.