Probabilitatea unui eveniment $A$ este raportul dintre numărul de rezultate favorabile pentru $A$ și numărul tuturor rezultatelor la fel de posibile
$P(A)=(m)/(n)$, unde $n$ este numărul total de rezultate posibile și $m$ este numărul de rezultate care favorizează $A$.
Probabilitatea unui eveniment este un număr din segmentul $$
Compania de taxi are 50$ de mașini disponibile. $35$ dintre ele sunt negre, restul sunt galbene. Găsiți probabilitatea ca o mașină galbenă să ajungă la un apel aleatoriu.
Aflați numărul de mașini galbene:
În total, sunt mașini de 50$, adică una din cincizeci va veni la apel. Există $15$ de mașini galbene, prin urmare, probabilitatea de sosire a unei mașini galbene este $(15)/(50)=(3)/(10)=0,3$
Răspuns: 0,3 USD
Evenimente opuse
Se spune că două evenimente sunt opuse dacă într-un proces dat sunt incompatibile și unul dintre ele are loc în mod necesar. Probabilitățile de evenimente opuse se adună la 1. Un eveniment opus evenimentului $A$ se scrie $((A))↖(-)$.
$P(A)+P((A))↖(-)=1$
Evenimente independente
Două evenimente $A$ și $B$ sunt numite independente dacă probabilitatea de apariție a fiecăruia dintre ele nu depinde de faptul dacă celălalt eveniment a avut loc sau nu. În caz contrar, evenimentele se numesc dependente.
Probabilitatea produsului a două evenimente independente $A$ și $B$ este egală cu produsul acestor probabilități:
$P(A B)=P(A) P(B)$
Ivan Ivanovici a cumpărat două bilete de loterie diferite. Probabilitatea ca primul să câștige bilet de loterie, este egal cu 0,15 USD. Probabilitatea ca al doilea bilet de loterie să câștige este de 0,12 USD. Ivan Ivanovici participă la ambele extrageri. Presupunând că extragerile au loc independent una de cealaltă, găsiți probabilitatea ca Ivan Ivanovici să câștige în ambele extrageri.
Probabilitate $P(A)$ - câștigă primul bilet.
Probabilitate $P(B)$ - câștigă al doilea bilet.
Evenimentele $A$ și $B$ sunt evenimente independente. Adică, pentru a găsi probabilitatea ca ambele evenimente să se producă, trebuie să găsiți produsul probabilităților
$P(A B)=P(A) P(B)$
$P=0,15 0,12=0,018$
Răspuns: 0,018 USD
Evenimente incompatibile
Se spune că două evenimente $A$ și $B$ sunt incompatibile dacă nu există rezultate care favorizează atât evenimentul $A$, cât și evenimentul $B$. (Evenimente care nu pot avea loc în același timp)
Probabilitatea sumei a două evenimente incompatibile $A$ și $B$ este egală cu suma probabilităților acestor evenimente:
$P(A+B)=P(A)+P(B)$
La examenul de algebră, studentul primește o întrebare din toate examenele. Probabilitatea ca aceasta să fie o întrebare pe tema " Ecuații cuadratice", este egal cu $0,3$. Probabilitatea ca aceasta să fie o întrebare pe tema " Ecuații iraționale", este egal cu 0,18 USD. Nu există întrebări legate de aceste două subiecte în același timp. Găsiți probabilitatea ca studentul să primească o întrebare pe unul dintre aceste două subiecte la examen.
Aceste evenimente sunt numite incompatibile, deoarece elevul va primi o întrebare FIE pe tema „Ecuații cuadriculare”, SAU pe tema „Ecuații iraționale”. Subiectele nu pot fi surprinse în același timp. Probabilitatea sumei a două evenimente incompatibile $A$ și $B$ este egală cu suma probabilităților acestor evenimente:
$P(A+B)=P(A)+P(B)$
$P \u003d 0,3 + 0,18 \u003d 0,48 $
Răspuns: 0,48 USD
Evenimente comune
Se spune că două evenimente sunt comune dacă apariția unuia dintre ele nu exclude apariția celuilalt în același proces. În caz contrar, evenimentele sunt numite incompatibile.
Probabilitatea sumei a două evenimente comune $A$ și $B$ este egală cu suma probabilităților acestor evenimente minus probabilitatea produsului lor:
$P(A+B)=P(A)+P(B)-P(A B)$
Există două aparate de cafea identice în holul cinematografului. Probabilitatea ca aparatul să rămână fără cafea până la sfârșitul zilei este de 0,6 USD. Probabilitatea ca ambele aparate să rămână fără cafea este de 0,32 USD. Găsiți probabilitatea ca cel puțin unul dintre automatele să rămână fără cafea până la sfârșitul zilei.
Să notăm evenimentele, să:
$A$ = cafeaua se va termina în prima mașină,
$B$ = cafeaua se va termina în a doua mașină.
$A B =$ cafeaua se va epuiza în ambele automate,
$A + B =$ cafeaua se va epuiza în cel puțin un automat.
Prin convenție, $P(A) = P(B) = 0,6; P(A B) = 0,32 USD.
Evenimentele $A$ și $B$ sunt comune, probabilitatea sumei a două evenimente comune este egală cu suma probabilităților acestor evenimente, redusă cu probabilitatea produsului lor:
$P(A + B) = P(A) + P(B) − P(A B) = 0,6 + 0,6 − 0,32 = 0,88$
Probabilitate. Sarcini ale examenului de profil la matematică.
Pregătit de un profesor de matematică la MBOU „Liceul nr. 4”, Ruzaevka
Ovchinnikova T.V.

Definiţia probability
Probabilitate evenimente A apelează raportul dintre numărul m rezultate favorabile pentru acest eveniment să numărul total n toate evenimentele incompatibile la fel de posibile care pot apărea ca urmare a unui singur test sau observație:
m
n
Lăsa k - numărul de aruncări de monede, apoi numărul de rezultate posibile: n=2 k .
Lăsa k - numărul de aruncări de zaruri, apoi numărul de rezultate posibile: n=6 k .

Într-un experiment aleatoriu, o monedă simetrică este aruncată de două ori. Găsiți probabilitatea ca capetele să apară exact o dată.
Soluţie.
Doar 4 variante: despre; oh oh; p p; p p; despre .
Favorabil 2: despre; R și R; despre .
Probabilitatea este 2/4 = 1/2 = 0,5 .
Răspuns: 0,5.

Într-un experiment aleatoriu, se aruncă două zaruri. Aflați probabilitatea de a obține 8 puncte în total. Rotunjiți rezultatul la cea mai apropiată sutime.
Soluţie.
Zarurile sunt zaruri cu 6 fețe. Primul zar poate arunca 1, 2, 3, 4, 5 sau 6 puncte. Fiecare opțiune de punctare corespunde cu 6 opțiuni de punctare pe al doilea zar.
Acestea. Total diverse opțiuni 6x6=36.
Opțiunile (rezultatele experimentului) vor fi următoarele:
1; 1 1; 2 1; 3 1; 4 1; 5 1; 6
2; 1 2; 2 2; 3 2; 4 2; 5 2; 6
etc. ...............................
6; 1 6; 2 6; 3 6; 4 6; 5 6; 6
Să numărăm numărul de rezultate (opțiuni) în care suma punctelor a două zaruri este 8.
2; 6 3; 5; 4; 4 5; 3 6; 2.
Doar 5 variante.
Să aflăm probabilitatea: 5/36 = 0,138 ≈ 0,14.
Răspuns: 0,14.

În colecția de bilete de biologie sunt în total 55 de bilete, 11 dintre ele conținând o întrebare despre botanică. Găsiți probabilitatea ca un student să primească o întrebare despre botanică într-un bilet de examen selectat aleatoriu.
Soluţie:
Probabilitatea ca un student să primească o întrebare despre botanică într-un bilet de examen selectat aleatoriu este 11/55 = 1/5 = 0,2.
Răspuns: 0,2.

La campionatul de gimnastică participă 20 de sportivi: 8 din Rusia, 7 din SUA, restul din China. Ordinea în care performanțele gimnastelor se stabilește prin tragere la sorți. Găsiți probabilitatea ca sportivul care concurează primul să fie din China.
Soluţie.
Sunt 20 de sportivi în total.
din care 20 - 8 - 7 = 5 sportivi din China.
Probabilitatea ca sportivul care concurează primul să fie din China este de 5/20 = 1/4 = 0,25.
Răspuns: 0,25.

Conferința științifică are loc în 5 zile. În total sunt planificate 75 de rapoarte - primele trei zile, câte 17 rapoarte fiecare, restul sunt distribuite în mod egal între a patra și a cincea zi. Ordinea rapoartelor este stabilită prin tragere la sorți. Care este probabilitatea ca raportul profesorului M. să fie programat pentru ultima zi a conferinței?
Soluţie:
Este programată ultima zi a conferinței
(75 - 17 × 3) : 2 = 12 rapoarte.
Probabilitatea ca raportul profesorului M. să fie programat pentru ultima zi a conferinței este de 12/75 = 4/25 = 0,16.
Răspuns: 0,16.

Înainte de începerea primei runde a campionatului de badminton, participanții sunt împărțiți aleatoriu în perechi de jocuri prin tragere la sorți. În total, 26 de jucători de badminton participă la campionat, inclusiv 10 participanți din Rusia, inclusiv Ruslan Orlov. Găsiți probabilitatea ca în primul tur Ruslan Orlov să joace cu vreun jucător de badminton din Rusia?
Soluţie:
De menționat că Ruslan Orlov trebuie să joace cu vreun jucător de badminton din Rusia. Și Ruslan Orlov însuși este și el din Rusia.
Probabilitatea ca în primul tur Ruslan Orlov să joace cu orice jucător de badminton din Rusia este de 9/25 = 36/100 = 0,36.
Răspuns: 0,36.

Dasha aruncă de două ori zaruri. Ea a marcat 8 puncte în total. Găsiți probabilitatea de a obține 2 la prima aruncare.
Soluţie.
În total, cele două zaruri ar trebui să arunce 8 puncte. Acest lucru este posibil dacă există următoarele combinații:
Doar 5 variante. Să numărăm numărul de rezultate (opțiuni) în care 2 puncte au căzut la prima rolă.
Această opțiune este 1.
Aflați probabilitatea: 1/5 = 0,2.
Răspuns: 0,2.

La Campionatul Mondial participă 20 de echipe. Cu ajutorul loturilor, ei trebuie împărțiți în cinci grupe a câte patru echipe fiecare. În cutie sunt cărți combinate cu numere de grup:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5.
Căpitanii de echipă trag câte o carte fiecare. Care este probabilitatea ca echipa rusă să fie în grupa a treia.
Soluţie:
Sunt 20 de echipe în total, 5 grupe.
Fiecare grupă are 4 echipe.
Deci, în total, am obținut 20 de rezultate, aveam nevoie de 4, ceea ce înseamnă că probabilitatea ca rezultatul dorit să cadă este 4/20 = 0,2.
Răspuns: 0,2.

Două fabrici produc aceeași sticlă pentru farurile auto. Prima fabrică produce 45% din acești ochelari, a doua - 55%. Prima fabrică produce 3% ochelari defecte, iar a doua - 1%. Găsiți probabilitatea ca un pahar cumpărat accidental dintr-un magazin să fie defect.
Soluţie:
Probabilitatea ca sticla să fi fost cumpărată la prima fabrică și să fie defectă:
R 1 = 0,45 0,03 = 0,0135.
Probabilitatea ca sticla să fi fost cumpărată la a doua fabrică și să fie defectă:
R 2 = 0,55 0,01 = 0,0055.
Prin urmare, conform formulei probabilitate deplină probabilitatea ca un pahar cumpărat accidental dintr-un magazin să fie defect este egală cu
p = p 1 + p 2 = 0,0135 + 0,0055 = 0,019.
Răspuns: 0,019.

Dacă marele maestru A. joacă alb, atunci el câștigă marele maestru B. cu o probabilitate de 0,52. Dacă A. joacă negru, atunci A. îl bate pe B. cu o probabilitate de 0,3.
Marii maeștri A. și B. joacă două jocuri, iar în al doilea joc schimbă culoarea pieselor. Aflați probabilitatea ca A. să câștige de ambele ori.
Soluţie:
Șansele de a câștiga primul și al doilea joc sunt independente unele de altele. Probabilitatea de a produce evenimente independente este egală cu produsul probabilităților lor:
p = 0,52 0,3 = 0,156.
Răspuns: 0,156.

Biatletul trage de cinci ori la ținte. Probabilitatea de a lovi ținta cu o singură lovitură este de 0,8. Găsiți probabilitatea ca biatletul să lovească ținta primele trei ori și să rateze ultimele două. Rotunjiți rezultatul la cea mai apropiată sutime.
Soluţie:
Rezultatul fiecărei lovituri următoare nu depinde de cele anterioare. Prin urmare, evenimentele „lovin la prima lovitură”, „lovin la a doua lovitură”, etc. independent.
Probabilitatea fiecărei lovituri este de 0,8. Deci probabilitatea unei rateuri este 1 - 0,8 = 0,2.
1 lovitură: 0,8
2 lovituri: 0,8
3 lovituri: 0,8
4 lovituri: 0,2
5 lovituri: 0,2
Conform formulei de înmulțire a probabilităților evenimentelor independente, constatăm că probabilitatea dorită este egală cu:
0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 = 0,02048 ≈ 0,02.
Răspuns: 0,02.

Magazinul are două automate de plată. Fiecare dintre ele poate fi defect cu o probabilitate de 0,05, indiferent de celălalt automat. Găsiți probabilitatea ca cel puțin un automat să fie funcțional.
Soluţie:
Găsiți probabilitatea ca ambele automate să fie defecte.
Aceste evenimente sunt independente, probabilitatea produsului lor este egală cu produsul probabilităților acestor evenimente:
0,05 0,05 = 0,0025.
Un eveniment constând în faptul că cel puțin un automat este util este opusul.
Prin urmare, probabilitatea sa este
1 − 0,0025 = 0,9975.
Răspuns: 0,9975.

Cowboy John lovește o muscă pe perete cu o probabilitate de 0,9 dacă trage cu un revolver. Dacă John trage un revolver neîmpușcat, el lovește o muscă cu o probabilitate de 0,2. Pe masă sunt 10 revolvere, dintre care doar 4 sunt împușcate. Cowboy John vede o muscă pe perete, apucă la întâmplare primul revolver pe care îl întâlnește și trage în muscă. Găsiți probabilitatea ca John să rateze.
Soluţie:
Probabilitatea ca John să rateze dacă apucă un revolver este:
0,4 (1 - 0,9) = 0,04
Probabilitatea ca John să rateze dacă apucă un revolver neîmpușcat este:
0,6 (1 - 0,2) = 0,48
Aceste evenimente sunt incompatibile, probabilitatea sumei lor este egală cu suma probabilităților acestor evenimente:
0,04 + 0,48 = 0,52.
Răspuns: 0,52.

În timpul tragerii de artilerie, sistemul automat efectuează o lovitură în țintă. Dacă ținta nu este distrusă, sistemul declanșează din nou. Loturile se repetă până când ținta este distrusă. Probabilitatea de a distruge o anumită țintă cu prima lovitură este de 0,4, iar la fiecare lovitură ulterioară este de 0,6. Câte lovituri vor fi necesare pentru a se asigura că probabilitatea de a distruge ținta este de cel puțin 0,98?
Soluţie:
Puteți rezolva problema „prin acțiuni”, calculând probabilitatea de a supraviețui după o serie de rateuri succesive:
P(1) = 0,6;
P(2) = P(1) 0,4 = 0,24;
P(3) = P(2) 0,4 = 0,096;
P(4) = P(3) 0,4 = 0,0384;
P(5) = P(4) 0,4 = 0,01536.
Ultima probabilitate este mai mică de 0,02, deci cinci lovituri la țintă sunt suficiente.
Raspuns: 5.

În clasă sunt 26 de persoane, printre care doi gemeni - Andrey și Sergey. Clasa este împărțită aleatoriu în două grupuri de câte 13 persoane fiecare. Găsiți probabilitatea ca Andrei și Serghei să fie în același grup.
Soluţie:
Lăsați unul dintre gemeni să fie într-un grup.
Împreună cu el vor fi în grup 12 persoane din cei 25 de colegi de clasă rămași.
Probabilitatea ca al doilea geamăn să fie printre aceste 12 persoane este egală cu
P=12:25=0,48.
Răspuns: 0,48.

Imaginea prezintă un labirint. Păianjenul se târăște în labirint în punctul „Intrare”. Păianjenul nu poate să se întoarcă și să se târască înapoi, prin urmare, la fiecare bifurcație, păianjenul alege una dintre căile pe care nu s-a târât încă. Presupunând că alegerea căii ulterioare este pur aleatorie, determinați cu ce probabilitate păianjenul va ajunge să iasă din D.
Soluţie:
La fiecare dintre cele patru bifurcări marcate, păianjenul poate alege fie calea care duce la ieșirea D, fie o altă cale cu o probabilitate de 0,5. Acestea sunt evenimente independente, probabilitatea produsului lor (păianjenul ajunge la ieșirea D) este egală cu produsul probabilităților acestor evenimente. Prin urmare, probabilitatea de a ajunge la ieșirea D este (0,5) 4 = 0,0625.
Prezentat până în prezent în banca deschisă a problemelor USE în matematică (mathege.ru), a căror soluție se bazează pe o singură formulă, care este o definiție clasică a probabilității.
Cel mai simplu mod de a înțelege formula este cu exemple.
Exemplul 1În coș sunt 9 bile roșii și 3 albastre. Bilele diferă doar prin culoare. La întâmplare (fără să ne uităm) primim unul dintre ele. Care este probabilitatea ca mingea aleasă în acest fel să fie albastră?
Cometariu.În problemele din teoria probabilității, ceva se întâmplă (în acest caz acțiunea noastră de a trage mingea), care poate avea rezultat diferit- rezultatul. Trebuie remarcat faptul că rezultatul poate fi vizualizat în moduri diferite. „Am scos o minge” este, de asemenea, un rezultat. „Am scos mingea albastră” este rezultatul. „Am extras această minge specială din toate mingile posibile” - această vedere cel mai puțin generalizată a rezultatului se numește rezultatul elementar. Rezultatele elementare sunt menite în formula de calcul a probabilității.
Soluţie. Acum calculăm probabilitatea de a alege o minge albastră.
Evenimentul A: „Mingea aleasă s-a dovedit a fi albastră”
Numărul total de toate rezultatele posibile: 9+3=12 (numărul de toate mingile pe care le-am putea extrage)
Numărul de rezultate favorabile pentru evenimentul A: 3 (numărul de astfel de rezultate în care a avut loc evenimentul A - adică numărul de bile albastre)
P(A)=3/12=1/4=0,25
Răspuns: 0,25
Să calculăm pentru aceeași problemă probabilitatea de a alege o minge roșie.
Numărul total de rezultate posibile va rămâne același, 12. Numărul de rezultate favorabile: 9. Probabilitatea dorită: 9/12=3/4=0,75
Probabilitatea oricărui eveniment este întotdeauna între 0 și 1.
Uneori, în vorbirea de zi cu zi (dar nu în teoria probabilității!) Probabilitatea evenimentelor este estimată ca procent. Tranziția între evaluarea matematică și cea conversațională se face prin înmulțirea (sau împărțirea) cu 100%.
Asa de,
În acest caz, probabilitatea este zero pentru evenimente care nu se pot întâmpla - improbabile. De exemplu, în exemplul nostru, aceasta ar fi probabilitatea de a extrage o minge verde din coș. (Numărul de rezultate favorabile este 0, P(A)=0/12=0 dacă sunt numărate conform formulei)
Probabilitatea 1 are evenimente care se vor întâmpla cu siguranță, fără opțiuni. De exemplu, probabilitatea ca „bila aleasă să fie fie roșie, fie albastră” este pentru problema noastră. (Număr de rezultate favorabile: 12, P(A)=12/12=1)
Ne-am uitat la un exemplu clasic care ilustrează definiția probabilității. Toate similare UTILIZAȚI sarcini conform teoriei probabilităților se rezolvă prin aplicarea acestei formule.
În loc de bile roșii și albastre, pot fi mere și pere, băieți și fete, bilete învățate și neînvățate, bilete care conțin sau nu o întrebare pe un subiect (prototipuri , ), genți defecte și de înaltă calitate sau pompe de grădină (prototipuri , ) - principiul rămâne același.
Diferă ușor în formularea problemei teoriei UTILIZAȚI probabilități, unde trebuie să calculați probabilitatea ca un eveniment să aibă loc într-o anumită zi. ( , ) Ca și în sarcinile anterioare, trebuie să determinați care este un rezultat elementar și apoi să aplicați aceeași formulă.
Exemplul 2 Conferința durează trei zile. În prima și a doua zi, câte 15 vorbitori, în a treia zi - 20. Care este probabilitatea ca raportul profesorului M. să cadă în a treia zi, dacă ordinea rapoartelor se stabilește prin tragere la sorți?
Care este rezultatul elementar aici? - Atribuirea unui raport al profesorului unuia dintre toate posibilele numere de serie pentru o performanță. La extragere participă 15+15+20=50 de persoane. Astfel, raportul profesorului M. poate primi unul din 50 de numere. Aceasta înseamnă că există doar 50 de rezultate elementare.
Care sunt rezultatele favorabile? - Cele în care se dovedește că profesorul va vorbi a treia zi. Adică ultimele 20 de numere.
Conform formulei, probabilitatea P(A)= 20/50=2/5=4/10=0,4
Răspuns: 0,4
Tragerea la sorți aici este stabilirea unei corespondențe aleatorii între oameni și locuri ordonate. În Exemplul 2, potrivirea a fost luată în considerare în ceea ce privește locurile pe care le-ar putea ocupa o anumită persoană. Poți aborda aceeași situație din cealaltă parte: care dintre persoanele cu ce probabilitate ar putea ajunge într-un anumit loc (prototipuri , , , ):
Exemplul 3 La tragere la sorți participă 5 germani, 8 francezi și 3 estonieni. Care este probabilitatea ca primul (/al doilea/al șaptelea/ultimul - nu contează) să fie un francez.
Numărul rezultatelor elementare este numărul tuturor oameni posibili care ar putea ajunge prin tragere la sorți în acest loc. 5+8+3=16 persoane.
Rezultate favorabile - francezi. 8 persoane.
Probabilitate dorită: 8/16=1/2=0,5
Răspuns: 0,5
Prototipul este puțin diferit. Există sarcini despre monede () și zaruri () care sunt ceva mai creative. Soluțiile la aceste probleme pot fi găsite pe paginile prototip.
Iată câteva exemple de aruncare a monedelor sau a zarurilor.
Exemplul 4 Când aruncăm o monedă, care este probabilitatea de a obține cozi?
Rezultatele 2 - capete sau cozi. (se crede că moneda nu cade niciodată pe margine) Rezultat favorabil - cozi, 1.
Probabilitate 1/2=0,5
Răspuns: 0,5.
Exemplul 5 Dacă aruncăm o monedă de două ori? Care este probabilitatea ca acesta să iasă în cap de ambele ori?
Principalul lucru este să stabilim ce rezultate elementare vom lua în considerare atunci când aruncăm două monede. După aruncarea a două monede, poate apărea unul dintre următoarele rezultate:
1) PP - de ambele ori a venit cozi
2) PO - prima dată cozi, a doua oară capete
3) OP - prima dată cap, a doua oară cozi
4) OO - heads up de ambele ori
Nu există alte opțiuni. Aceasta înseamnă că există 4 rezultate elementare. Doar primul este favorabil, 1.
Probabilitate: 1/4=0,25
Răspuns: 0,25
Care este probabilitatea ca două aruncări ale unei monede să cadă pe cozi?
Numărul de rezultate elementare este același, 4. Rezultatele favorabile sunt al doilea și al treilea, 2.
Probabilitatea de a obține o coadă: 2/4=0,5
În astfel de probleme, o altă formulă poate fi utilă.
Dacă la o aruncare a unei monede avem 2 rezultate posibile, atunci pentru două aruncări de rezultate vor fi 2 2=2 2 =4 (ca în exemplul 5), pentru trei aruncări 2 2 2=2 3 =8, pentru patru : 2·2·2·2=2 4 =16, … pentru N aruncări de rezultate posibile vor fi 2·2·...·2=2 N .
Deci, puteți găsi probabilitatea de a obține 5 cozi din 5 aruncări de monede.
Numărul total de rezultate elementare: 2 5 =32.
Rezultate favorabile: 1. (RRRRRR - toate cele 5 ori cozi)
Probabilitate: 1/32=0,03125
Același lucru este valabil și pentru zaruri. Cu o singură aruncare sunt posibile 6 rezultate.Deci, pentru două aruncări: 6 6=36, pentru trei 6 6 6=216 etc.
Exemplul 6 Aruncăm un zar. Care este probabilitatea de a obține un număr par?
Rezultate totale: 6, în funcție de numărul de fețe.
Favorabil: 3 rezultate. (2, 4, 6)
Probabilitate: 3/6=0,5
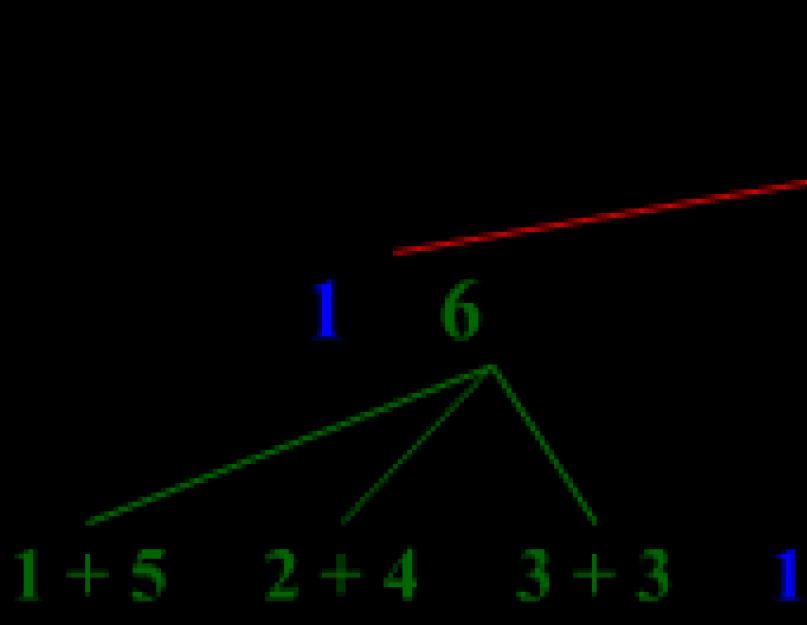
Exemplul 7 Aruncă două zaruri. Care este probabilitatea ca totalul să fie 10? (rotunjit la sutimi)
Există 6 rezultate posibile pentru un zar. Prin urmare, pentru doi, conform regulii de mai sus, 6·6=36.
Ce rezultate vor fi favorabile ca un total de 10 să cadă?
10 trebuie descompus în suma a două numere de la 1 la 6. Acest lucru se poate face în două moduri: 10=6+4 și 10=5+5. Deci, pentru cuburi, sunt posibile opțiuni:
(6 pe primul și 4 pe al doilea)
(4 pe primul și 6 pe al doilea)
(5 pe primul și 5 pe al doilea)
În total, 3 opțiuni. Probabilitate dorită: 3/36=1/12=0,08
Răspuns: 0,08
Alte tipuri de probleme B6 vor fi discutate în unul dintre următoarele articole „Cum se rezolvă”.
eveniment aleatoriu Orice eveniment care poate sau nu să apară ca urmare a unei anumite experiențe.
Probabilitatea evenimentului R este egal cu raportul dintre numărul de rezultate favorabile k dintre toate rezultatele posibile. n, adică
p=\frac(k)(n)
Formule de adunare și înmulțire a probabilităților
eveniment \bar(A). numit opus evenimentului A, dacă evenimentul A nu a avut loc.
Suma probabilităților evenimente opuse este egal cu unul, i.e.
P(\bar(A)) + P(A) =1
- Probabilitatea unui eveniment nu poate fi mai mare de 1.
- Dacă probabilitatea unui eveniment este 0, atunci nu se va întâmpla.
- Dacă probabilitatea unui eveniment este 1, atunci se va întâmpla.
Teorema de adunare a probabilității:
„Probabilitatea sumei a două evenimente incompatibile este egală cu suma probabilităților acestor evenimente.”
P(A+B) = P(A) + P(B)
Probabilitate sume două evenimente comune este egală cu suma probabilităților acestor evenimente fără a lua în considerare apariția lor comună:
P(A+B) = P(A) + P(B) - P(AB)
Teorema înmulțirii probabilităților
„Probabilitatea produsului a două evenimente este egală cu produsul probabilităților unuia dintre ele prin probabilitate condițională altul, calculat cu condiția ca primul să aibă loc.
P(AB)=P(A)*P(B)
Evoluții numit incompatibil, dacă apariţia unuia dintre ele exclude apariţia altora. Adică, poate avea loc un singur eveniment anume sau altul.
Evoluții numit comun, cu excepția cazului în care apariția unuia dintre ele împiedică apariția celuilalt.
Două evenimente aleatorii A și B sunt numite independent, dacă apariţia unuia dintre ele nu modifică probabilitatea apariţiei celuilalt. În caz contrar, evenimentele A și B se numesc dependente.