Matematikte önemli bir kavram fonksiyondur. Onun yardımıyla doğada meydana gelen birçok süreci görsel olarak temsil edebilir ve belirli miktarlar arasındaki ilişkiyi formüller, tablolar ve resimler kullanarak bir grafik üzerinde yansıtabilirsiniz. Bir örnek, bir sıvı tabakasının bir cisim üzerindeki basıncının daldırma derinliğine, belirli bir kuvvetin bir nesne üzerindeki etkisine ivmelenmesine, aktarılan enerji üzerindeki sıcaklıktaki bir artışa ve diğer birçok sürece bağlı olmasıdır. Bir fonksiyonu incelemek, bir grafik oluşturmayı, özelliklerini, tanım alanını ve değerlerini, artış ve azalma aralıklarını bulmayı içerir. Önemli bir nokta Bu süreçte ekstrem noktaları bulmaktır. Bunun nasıl doğru bir şekilde yapılacağı hakkında daha fazla konuşacağız.
Belirli bir örnek kullanarak konseptin kendisi hakkında
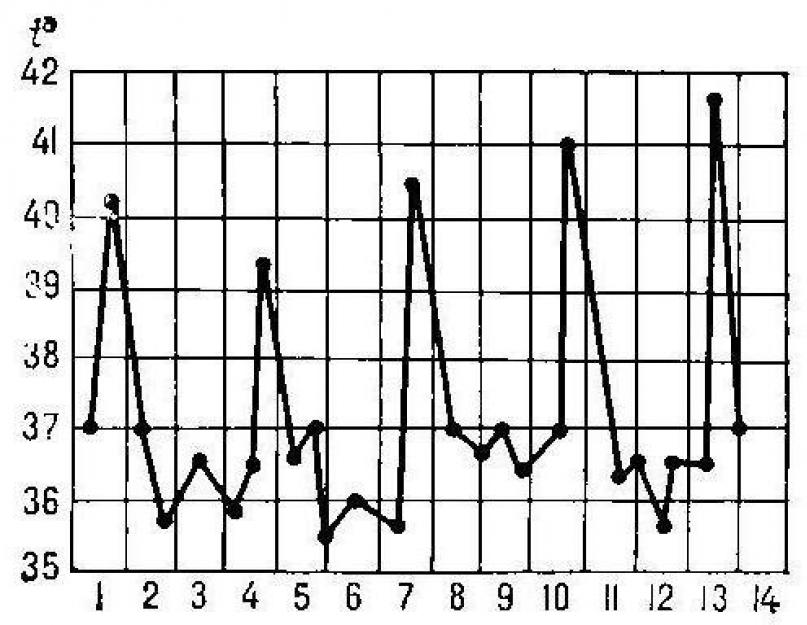
Tıpta, bir fonksiyon grafiğinin çizilmesi, hastanın vücudundaki hastalığın ilerleyişi hakkında bize bilgi verebilir ve durumunu açıkça yansıtabilir. OX ekseninin gün cinsinden zamanı, OU ekseninin ise insan vücut sıcaklığını temsil ettiğini varsayalım. Şekil, bu göstergenin nasıl keskin bir şekilde yükselip sonra düştüğünü açıkça göstermektedir. Daha önce artan fonksiyonun azalmaya başladığı veya tam tersi anları yansıtan özel noktaları fark etmek de kolaydır. Bunlar ekstrem noktalardır, yani kritik değerlerdir (maksimum ve minimum). bu durumda hastanın sıcaklığı ve ardından durumunda değişiklikler meydana gelir.

Eğim açısı
Fonksiyonun türevinin nasıl değiştiğini şekilden kolayca belirleyebilirsiniz. Grafiğin düz çizgileri zamanla yukarı doğru çıkıyorsa bu pozitiftir. Ve ne kadar dik olurlarsa, daha yüksek değer eğim açısı arttıkça türevi alır. Bu değerin azaldığı dönemlerde negatif değerler, ekstremum noktalarında sıfıra döner ve ikinci durumda türevin grafiği OX eksenine paralel olarak çizilir.
Diğer tüm işlemler aynı şekilde ele alınmalıdır. Ancak bu kavramı tanımlamanın en iyi yolu hareket etmektir. farklı bedenler grafiklerde açıkça görülmektedir.
Hareket
Bir nesnenin düzgün bir şekilde hızlanarak düz bir çizgide hareket ettiğini varsayalım. Bu dönemde vücudun koordinatlarındaki değişiklik, matematikçilerin parabolün dalı olarak adlandıracağı belirli bir eğri ile grafiksel olarak temsil edilir. Aynı zamanda koordinat göstergeleri her saniye daha hızlı değiştiği için fonksiyon sürekli artmaktadır. Hız grafiği, değeri de artan türevin davranışını gösterir. Bu, hareketin kritik noktalarının olmadığı anlamına gelir.
Bu süresiz olarak devam edecekti. Peki ya vücut aniden yavaşlamaya, durmaya ve farklı bir yöne doğru hareket etmeye karar verirse? Bu durumda koordinat göstergeleri azalmaya başlayacaktır. Ve fonksiyon kritik bir değeri geçerek artandan azalan tarafa dönecektir.

Bu örneği kullanarak, bir fonksiyonun grafiğindeki uç noktaların, monotonluğun sona erdiği anlarda ortaya çıktığını bir kez daha anlayabilirsiniz.
Türevin fiziksel anlamı
Daha önce anlatılanlar, türevin aslında fonksiyonun değişim oranı olduğunu açıkça gösterdi. Bu açıklama fiziksel anlamını içermektedir. Ekstrem noktalar grafikteki kritik alanlardır. Sıfıra eşit olduğu ortaya çıkan türevin değeri hesaplanarak tanımlanabilir ve tespit edilebilirler.
Bir ekstremum için yeterli koşul olan başka bir işaret daha vardır. Bu tür dönüm noktalarındaki türev işaretini maksimum alanda “+”dan “-”ye, minimum alanda “-”den “+”ya değiştirir.

Yer çekimi etkisi altında hareket
Başka bir durum hayal edelim. Topla oynayan çocuklar, topu ufka doğru açılı hareket edecek şekilde fırlattılar. İlk anda hız bu nesnenin en büyüğüydü, ancak yerçekiminin etkisi altında azalmaya başladı ve her saniyede aynı miktarda yaklaşık 9,8 m/s2'ye eşit oldu. Bu, serbest düşüş sırasında yer çekiminin etkisi altında oluşan ivmenin değeridir. Ay'da yaklaşık altı kat daha küçük olurdu.
Bir cismin hareketini tanımlayan grafik, dalları aşağıya bakan bir paraboldür. Ekstrem noktalar nasıl bulunur? Bu durumda cismin (topun) hızının sıfır değerini aldığı fonksiyonun tepe noktasıdır. Fonksiyonun türevi sıfır olur. Bu durumda yön ve dolayısıyla hız değeri ters yönde değişir. Vücut her saniye daha hızlı uçuyor ve aynı miktarda - 9,8 m/s 2 - hızlanıyor.

İkinci türev
Önceki durumda hız modülü grafiği düz bir çizgi olarak çizilmiştir. Bu değerin değeri sürekli azaldığı için bu çizgi başlangıçta aşağıya doğru yönlendirilir. Bir noktada sıfıra ulaştıktan sonra bu değerin göstergeleri artmaya başlar ve hız modülünün grafiksel gösteriminin yönü önemli ölçüde değişir. Çizgi şu anda yukarıyı gösteriyor.
Koordinatın zamana göre türevi olan hızın da kritik bir noktası vardır. Bu bölgede başlangıçta azalan fonksiyon artmaya başlar. Bu, fonksiyonun türevinin uç noktasının konumudur. Bu durumda teğetin eğim açısı sıfır olur. Koordinatın zamana göre ikinci türevi olan ivme ise işareti “-”den “+”ya değiştirir. Ve hareket eşit derecede yavaştan eşit şekilde hızlanmaya başlar.
Hızlanma grafiği
Şimdi dört resme bakalım. Her biri zaman içindeki değişikliklerin bir grafiğini görüntüler; fiziksel miktar hızlanma gibi. “A” durumunda değeri pozitif ve sabit kalır. Bu, vücudun koordinatları gibi hızının da sürekli arttığı anlamına gelir. Nesnenin sonsuz uzun bir süre bu şekilde hareket edeceğini hayal edersek, koordinatın zamana bağımlılığını yansıtan fonksiyonun sürekli arttığı ortaya çıkacaktır. Buradan kritik bölgelerinin olmadığı sonucu çıkıyor. Ayrıca türevin grafiğinde, yani hızın doğrusal olarak değiştiği uç noktalar da yoktur.

Aynı durum pozitif ve sürekli artan ivmeli “B” durumu için de geçerlidir. Doğru, buradaki koordinat ve hız grafikleri biraz daha karmaşık olacak.
İvme sıfıra gittiğinde
“B” şekline bakıldığında vücudun hareketini karakterize eden tamamen farklı bir resim görülebilir. Hızı, dalları aşağı doğru yönlendirilmiş bir parabol ile grafiksel olarak temsil edilecektir. İvme değişimini anlatan çizgiyi OX ekseni ile kesişinceye kadar devam ettirirsek ve daha da ileriye gidersek, ivmenin sıfır olduğu bu kritik değere kadar cismin hızının giderek daha yavaş artacağını hayal edebiliriz. . Koordinat fonksiyonunun türevinin uç noktası tam olarak parabolün tepe noktasında olacaktır, bundan sonra vücut hareketinin doğasını kökten değiştirecek ve farklı bir yönde hareket etmeye başlayacaktır.
Son durumda, “G”, hareketin niteliği kesin olarak belirlenemez. Burada yalnızca söz konusu dönem için herhangi bir ivmelenmenin olmadığını biliyoruz. Bu, nesnenin yerinde kalabileceği veya sabit bir hızla hareket edebileceği anlamına gelir.
Koordinat ekleme problemi
Okulda cebir okurken sıklıkla karşılaşılan ve Birleşik Devlet Sınavına hazırlık için sunulan görevlere geçelim. Aşağıdaki şekil fonksiyonun grafiğini göstermektedir. Ekstrem noktaların toplamını hesaplamak gerekir.

Fonksiyonun özelliklerinde değişiklik gözlemlenen kritik alanların koordinatlarını belirleyerek ordinat ekseni için bunu yapalım. Basitçe söylemek gerekirse, dönüm noktaları için OX ekseni boyunca değerleri bulacağız ve ardından elde edilen terimleri eklemeye devam edeceğiz. Grafiğe göre şu değerleri aldıkları görülmektedir: -8; -7; -5; -3; -2; 1; 3. Bunun toplamı -21 olur, cevap budur.
Optimum çözüm
Pratik görevlerin yerine getirilmesinde en uygun çözümün seçiminin ne kadar önemli olabileceğini açıklamaya gerek yok. Sonuçta, bir hedefe ulaşmanın birçok yolu vardır, ancak kural olarak en iyi çıkış yolu yalnızca bir tanesidir. Bu, örneğin gemileri tasarlarken son derece gereklidir. uzay gemileri ve uçak, mimari yapılar bu insan yapımı nesnelerin en uygun şeklini bulmak için.

Araçların hızı büyük ölçüde su ve havada hareket ederken karşılaştıkları direncin, yerçekimi kuvvetlerinin ve diğer birçok göstergenin etkisi altında ortaya çıkan aşırı yüklerin uygun şekilde en aza indirilmesine bağlıdır. Denizdeki bir gemi, fırtına sırasında stabilite gibi niteliklere ihtiyaç duyar; bir nehir gemisi için minimum su çekimi önemlidir. Optimum tasarımı hesaplarken grafikteki uç noktalar, karmaşık bir problemin en iyi çözümü hakkında görsel olarak fikir verebilir. Bu tür sorunlar genellikle ekonomide, iş alanlarında ve diğer birçok yaşam durumunda çözülür.
Antik tarihten
Eski bilgeler bile aşırı sorunlarla meşguldü. Yunan bilim adamları matematiksel hesaplamalar yoluyla alanların ve hacimlerin gizemini başarıyla çözdüler. Aynı çevreye sahip çeşitli şekillerden oluşan bir düzlemde, bunu ilk anlayanlar onlardı. en büyük alan her zaman bir dairesi vardır. Benzer şekilde top, uzaydaki aynı yüzey alanına sahip diğer nesneler arasında maksimum hacme sahiptir. Aşağıdaki kişiler kendilerini bu tür sorunları çözmeye adadılar: ünlü kişilikler Arşimet, Öklid, Aristoteles, Apollonius gibi. Heron uç noktaları bulmada mükemmeldi ve hesaplamaları kullanarak ustaca cihazlar yaptı. Bunlar arasında buharla hareket eden makineler, pompalar ve aynı prensiple çalışan türbinler yer alıyordu.

Kartaca İnşaatı
Konusu aşırı sorunlardan birinin çözümüne dayanan bir efsane var. Yardım için bilgelere başvuran Fenikeli prensesin gösterdiği iş yaklaşımının sonucu Kartaca'nın inşası oldu. Arsa Bu antik ve ünlü şehir için Dido (hükümdarın adıydı) Afrika kabilelerinden birinin lideri tarafından verildi. Sözleşmeye göre öküz derisiyle kaplanması gerektiğinden, tahsis alanı ilk başta ona çok büyük görünmedi. Ancak prenses askerlerine onu ince şeritler halinde kesip kemer yapmalarını emretti. O kadar uzun olduğu ortaya çıktı ki, bütün bir şehrin sığabileceği bir alanı kaplıyordu.
Matematiksel analizin kökenleri
Şimdi eski zamanlardan daha yakın bir döneme geçelim. Kepler'in matematiksel analizin temellerini 17. yüzyılda bir şarap satıcısıyla yaptığı toplantıyla anlamaya başlaması ilginçtir. Tüccar mesleğinde o kadar bilgiliydi ki, fıçıdaki içeceğin hacmini, içine demir bir halat indirerek kolayca belirleyebiliyordu. Böyle bir merak üzerine düşünen ünlü bilim adamı, bu ikilemi kendi başına çözmeyi başardı. O zamanların yetenekli fıçıcılarının, sabitleme halkalarının çevresinin belirli bir yüksekliğinde ve yarıçapında maksimum kapasiteye sahip olacak şekilde kap yapma becerisine sahip oldukları ortaya çıktı.
Bu Kepler'in daha fazla düşünmesine neden oldu. Cooper'lar uzun araştırmalar, hatalar ve yeni denemeler sonucunda en uygun çözüme ulaşarak deneyimlerini nesilden nesile aktardılar. Ancak Kepler, süreci hızlandırmak ve matematiksel hesaplamalar yoluyla aynı şeyin kısa sürede nasıl yapılacağını öğrenmek istiyordu. Meslektaşları tarafından toplanan tüm gelişmeler artık ünlü Fermat ve Newton-Leibniz teoremlerine dönüştü.
Maksimum alan sorunu
Uzunluğu 50 cm olan bir telimiz olduğunu düşünelim. Bundan en büyük alana sahip bir dikdörtgeni nasıl yapabiliriz?
Bir karara başlarken herkesin bildiği basit gerçeklerden yola çıkmalısınız. Figürümüzün çevresinin 50 cm olacağı açıktır. Her iki kenar uzunluğunun iki katı uzunluktadır. Bu, bunlardan biri “X” olarak gösterilerek diğerinin (25 - X) olarak ifade edilebileceği anlamına gelir.
Buradan X(25 - X)'e eşit bir alan elde ederiz. Bu ifade birden fazla değer alan bir fonksiyon gibi düşünülebilir. Sorunu çözmek, bunların maksimumunu bulmayı gerektirir, bu da uç noktaları bulmanız gerektiği anlamına gelir.
Bunu yapmak için birinci türevi bulup sıfıra eşitliyoruz. Sonuç basit bir denklemdir: 25 - 2X = 0.
Buradan kenarlardan birinin X = 12,5 olduğunu öğreniyoruz.
Dolayısıyla diğeri: 25 - 12,5 = 12,5.
Sorunun çözümünün bir kenarı 12,5 cm olan bir kare olacağı ortaya çıktı.

Maksimum hız nasıl bulunur?
Başka bir örneğe bakalım. Doğrusal hareketi S = - t 3 + 9t 2 - 24t - 8 denklemiyle tanımlanan, kat edilen mesafenin metre cinsinden ve zamanın saniye cinsinden ifade edildiği bir cisim olduğunu hayal edelim. Maksimum hızı bulmamız gerekiyor. Bu nasıl yapılır? İndirdiğimizde hızı yani birinci türevi buluyoruz.
Denklemi elde ederiz: V = - 3t 2 + 18t - 24. Şimdi sorunu çözmek için yine ekstrem noktaları bulmamız gerekiyor. Bu, önceki görevde olduğu gibi yapılmalıdır. Hızın birinci türevini bulup sıfıra eşitliyoruz.
Şunu elde ederiz: - 6t + 18 = 0. Dolayısıyla t = 3 s. Bu, vücudun hızının kritik bir değere ulaştığı zamandır. Ortaya çıkan verileri hız denkleminde yerine koyarız ve şunu elde ederiz: V = 3 m/s.
Ama ne olduğunu nasıl anlıyorsunuz? maksimum hızÇünkü bir fonksiyonun kritik noktaları onun en büyük veya en küçük değerleri olabilir mi? Kontrol etmek için hızın ikinci türevini bulmanız gerekir. Eksi işaretiyle 6 sayısı olarak ifade edilir. Bu, bulunan noktanın maksimum olduğu anlamına gelir. Pozitif bir değer olması durumunda ikinci türevin minimumu olacaktır. Bu, bulunan çözümün doğru olduğu anlamına gelir.
Örnek olarak verilen problemler, bir fonksiyonun ekstremum noktalarını nasıl bulacağınızı bildiğiniz takdirde çözülebilecek problemlerin sadece bir kısmıdır. Aslında bunlardan çok daha fazlası var. Ve böyle bir bilgi, insan uygarlığı için sınırsız olanaklar açar.
Gördüğünüz gibi, bir fonksiyonun ekstremumunun bu işareti, o noktada en azından ikinci dereceden bir türevin varlığını gerektirir.
Örnek.
Fonksiyonun ekstremumunu bulun.
Çözüm.
Tanım alanıyla başlayalım: 
Orijinal fonksiyonun türevini alalım: 
x=1 yani bu olası bir ekstremum noktasıdır. Fonksiyonun ikinci türevini bulup değerini hesaplıyoruz.:

x = 1 x=1 Bu nedenle, bir ekstremum için ikinci yeterli koşula göre,  - maksimum nokta. Daha sonra
- maksimum nokta. Daha sonra
- maksimum işlev.

Grafik illüstrasyon.
![]()
Cevap:
Bir fonksiyonun ekstremumu için üçüncü yeterli koşul. Fonksiyona izin ver y=f(x) kadar türevleri vardır N Noktanın -komşuluğundaki -inci mertebeden ve türevlere kadar n+1
Örnek.
-th'inci sıra noktanın kendisinde. Bırak olsun. ![]() .
.
Çözüm.
Fonksiyonun ekstremum noktalarını bulun
Orijinal fonksiyon rasyonel bir tam fonksiyondur; tanım alanı, gerçek sayılar kümesinin tamamıdır. 
Fonksiyonun türevini alalım: ![]() dolayısıyla bunlar olası ekstremum noktalarıdır. Bir ekstremum için üçüncü yeterli koşulu kullanalım.
dolayısıyla bunlar olası ekstremum noktalarıdır. Bir ekstremum için üçüncü yeterli koşulu kullanalım.
İkinci türevi buluyoruz ve değerini olası ekstrem noktalarda hesaplıyoruz (ara hesaplamaları atlayacağız): 
Sonuç olarak, maksimum noktadır (ekstremumun üçüncü yeterli işareti için elimizdeki n=1 Ve ).
Noktaların doğasını öğrenmek için ![]() üçüncü türevi buluyoruz ve değerini şu noktalarda hesaplıyoruz:
üçüncü türevi buluyoruz ve değerini şu noktalarda hesaplıyoruz: 
Bu nedenle, fonksiyonun dönüm noktasıdır ( n=2 Ve ).
Geriye bu konuyla ilgilenmek kalıyor. Bu noktada dördüncü türevi bulup değerini hesaplıyoruz: 
Bu nedenle fonksiyonun minimum noktasıdır.
- maksimum işlev.

Grafik illüstrasyon.
Maksimum nokta fonksiyonun minimum noktasıdır.
10. Bir fonksiyonun ekstremumu Bir ekstremun tanımı
y = f(x) fonksiyonu çağrılır artan (azalan) belirli bir aralıkta, eğer x 1 için< x 2 выполняется неравенство (f(x 1) < f (x 2) (f(x 1) >f(x2)).
Türevlenebilir fonksiyon y = f(x) bir aralıkta artarsa (azalırsa), bu aralıktaki türevi f " (x) 0
(f" (x) = 0).
Nokta X O isminde yerel maksimum nokta (minimum) f(x) fonksiyonu, eğer noktanın bir komşuluğu varsa X O f(x) ≤ f(x о) (f(x) ≥ f(x о)) eşitsizliğinin doğru olduğu tüm noktalar için.
Maksimum ve minimum noktalara denir ekstrem noktalar ve fonksiyonun bu noktalardaki değerleri onun aşırılıklar.
Ekstrem noktalar
Bir ekstremum için gerekli koşullar. Eğer nokta X O f(x) fonksiyonunun bir uç noktası ise, bu durumda ya f " (x o) = 0 olur ya da f (x o) mevcut olmaz. Bu tür noktalara denir kritik, ve fonksiyonun kendisi kritik noktada tanımlanır. Bir fonksiyonun ekstremum değerleri kritik noktaları arasında aranmalıdır.
İlk yeterli koşul.İzin vermek X O- kritik nokta. Eğer f "(x) bir noktadan geçerken X O artı işaretini eksi olarak değiştirir, ardından bu noktada X O fonksiyonun bir maksimumu vardır, aksi takdirde bir minimumu vardır. Kritik noktadan geçerken türev işaret değiştirmezse, o noktada X O aşırı bir durum yok.
İkinci yeterli koşul. f(x) fonksiyonunun noktanın yakınında bir f " (x) türevi olsun X O ve noktanın kendisindeki ikinci türev X O. Eğer f "(x o) = 0, >0 (<0), то точка X O f(x) fonksiyonunun yerel minimum (maksimum) noktasıdır. =0 ise ya ilk yeterli koşulu kullanmanız ya da daha yüksek türevleri kullanmanız gerekir.
Bir parça üzerinde y = f(x) fonksiyonu minimum veya maksimum değerine kritik noktalarda veya parçanın uçlarında ulaşabilir.
Örnek 3.22. f(x) = 2x 3 - 15x 2 + 36x - 14 fonksiyonunun ekstremumunu bulun.
Çözüm. F "(x) = 6x 2 - 30x +36 = 6(x -2)(x - 3) olduğundan, x 1 = 2 ve x 2 = 3 fonksiyonunun kritik noktaları. Ekstrem yalnızca şu şekilde olabilir: x 1 = 2 noktasından geçerken türevin işareti artıdan eksiye değiştiği için, bu noktada fonksiyon bir maksimuma sahiptir. x 2 = 3 noktasından geçerken türevin işareti eksiden değişir. artıya, dolayısıyla x 2 = 3 noktasında fonksiyonun minimum değeri vardır. Fonksiyonun x 1 = 2 ve x 2 = 3 noktalarındaki değerlerini hesapladıktan sonra fonksiyonun ekstremumunu buluruz: maksimum f( 2) = 14 ve minimum f(3) = 13.
Sürekli bir fonksiyonun grafiğini düşünün Fonksiyona izin verşekilde gösterilmiştir.
Bir noktada fonksiyon değeri X 1, hem solundaki hem de sağındaki tüm komşu noktalardaki fonksiyon değerlerinden büyük olacaktır X 1. Bu durumda fonksiyonun şu noktada olduğunu söylüyoruz. X Maksimum 1. bu noktada X Fonksiyon 3'ün de bir maksimumu olduğu açıktır. konuyu ele alırsak X 2 ise, içindeki fonksiyon değeri tüm komşu değerlerden küçüktür. Bu durumda fonksiyonun şu noktada olduğunu söylüyoruz. X 2 minimum. Aynı şekilde nokta için X 4 .
İşlev Fonksiyona izin ver bu noktada X 0 var maksimum, eğer fonksiyonun bu noktadaki değeri, o noktayı içeren bir aralığın tüm noktalarındaki değerlerinden büyükse X 0, yani eğer bir noktanın böyle bir komşuluğu varsa X 0, herkes içindir X≠X 0 , bu mahalleye ait eşitsizlik devam ediyor f(x)<f(x 0 ) .
İşlev Fonksiyona izin ver sahip olmak minimum bu noktada X 0 , eğer bir noktanın böyle bir komşuluğu varsa X 0 , bu herkes için X≠X 0 bu mahalleye ait, eşitsizlik geçerli f(x)>f(x 0.
Fonksiyonun maksimum ve minimum değerine ulaştığı noktalara ekstrem noktalar, fonksiyonun bu noktalardaki değerlerine ise fonksiyonun ekstremum değerleri denir.
Bir parça üzerinde tanımlanan bir fonksiyonun maksimum ve minimum değerlerine ancak söz konusu parçanın içerdiği noktalarda ulaşabileceğine dikkat edelim.
Bir fonksiyonun bir noktada maksimuma sahip olması, o noktada fonksiyonun tüm tanım alanında en büyük değere sahip olduğu anlamına gelmediğini unutmayın. Yukarıda tartışılan şekilde, noktadaki fonksiyon X 1'in maksimum değeri vardır, ancak fonksiyon değerlerinin noktadan daha büyük olduğu noktalar vardır X 1 . özellikle, F(X 1) < F(X 4) yani Bir fonksiyonun minimumu maksimumundan büyüktür. Maksimumun tanımından yalnızca bunun, fonksiyonun maksimum noktasına yeterince yakın noktalardaki en büyük değeri olduğu sonucu çıkar.
Teorem 1. (Bir ekstremun varlığı için gerekli koşul.) Diferansiyellenebilir fonksiyon ise Fonksiyona izin verşu noktada var x=x ekstremum 0 ise bu noktadaki türevi sıfır olur.
Kanıt. Kesinlik için şu noktada X 0 fonksiyonunun maksimumu vardır. Daha sonra, yeterince küçük artışlar için Δ X sahibiz f(x 0 + Δ X)
Bu eşitsizlikleri Δ'daki limite geçirmek X→ 0 ve türev dikkate alındığında F "(X 0) vardır ve bu nedenle soldaki limit Δ'nın nasıl olduğuna bağlı değildir. X→ 0, şunu elde ederiz: Δ'da X → 0 – 0 F"(X 0) ≥ 0 a'da Δ X → 0 + 0 F"(X 0) ≤ 0. Çünkü F"(X 0) bir sayıyı tanımlıyorsa bu iki eşitsizlik ancak şu durumlarda uyumludur: F"(X 0) = 0.
Kanıtlanmış teorem, maksimum ve minimum noktaların yalnızca türevin sıfır olduğu argümanın değerleri arasında bulunabileceğini belirtir.
Bir fonksiyonun belirli bir parçanın tüm noktalarında türevinin olduğu durumu düşündük. Türevin bulunmadığı durumlarda durum nedir? Örneklere bakalım.
Örnekler.
- sen=|X|.
Fonksiyonun bu noktada türevi yoktur X=0 (bu noktada fonksiyonun grafiğinin tanımlanmış bir teğeti yoktur), ancak bu noktada fonksiyonun bir minimumu vardır, çünkü sen(0)=0 ve tümü için X≠ 0sen > 0.
- İzin vermek X< x
0. Daha sonra C< x
0 ve f "(c)> 0.
Bu yüzden f "(c)(x- x 0)<
0 ve dolayısıyla
f(x) - f(x) 0 )< 0, yani f(x)< f(x 0 ).
- İzin vermek x > x 0. Daha sonra c>x 0 ve f "(c)< 0. Araç f "(c)(x- x 0)< 0. Bu yüzden f(x) - f(x) 0 ) <0,т.е.f(x)< f(x 0 ) .
- Bir fonksiyonun tanım kümesini bulun f(x).
- Bir fonksiyonun ilk türevini bulun f "(x).
- Bunun için kritik noktaları belirleyin:
- Denklemin gerçek köklerini bulun f "(x)=0;
- tüm değerleri bul X bunun için türev f "(x) mevcut değil.
- Kritik noktanın solunda ve sağında türevin işaretini belirleyin. Türevin işareti iki kritik nokta arasında sabit kaldığından, türevin işaretini kritik noktanın bir noktasında solunda ve bir noktasında sağında belirlemek yeterlidir.
- Fonksiyonun ekstrem noktalardaki değerini hesaplayın.
- Fonksiyonun aralıktaki tüm kritik noktalarını bulun ( a, b) ve bu noktalardaki fonksiyon değerlerini hesaplayın.
- Segmentin uçlarındaki fonksiyonun değerlerini hesaplayın. x = a, x = b.
- Elde edilen tüm değerlerden en büyüğünü ve en küçüğünü seçin.

Fonksiyonun türevi yoktur X=0, sonsuza gittiği için X=0. Ancak bu noktada fonksiyonun maksimumu vardır.
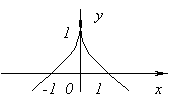
Fonksiyonun türevi yoktur X=0, çünkü ![]() en X→0. Bu noktada fonksiyonun ne maksimumu ne de minimumu vardır. Gerçekten mi, f(x)=0 ve X<0f(x)<0, а при X>0f(x)>0.
en X→0. Bu noktada fonksiyonun ne maksimumu ne de minimumu vardır. Gerçekten mi, f(x)=0 ve X<0f(x)<0, а при X>0f(x)>0.

Dolayısıyla verilen örneklerden ve formüle edilen teoremden, bir fonksiyonun yalnızca iki durumda bir ekstremuma sahip olabileceği açıktır: 1) türevin mevcut olduğu ve sıfıra eşit olduğu noktalarda; 2) Türevin bulunmadığı noktada.
Ancak eğer bir noktada X 0 bunu biliyoruz f "(x 0 ) =0 ise bundan şu noktada sonuç çıkarılamaz: X 0 fonksiyonun bir ekstremumu vardır.
Örneğin. ![]() .
.

Ama dönem X=0 bir ekstrem nokta değildir, çünkü bu noktanın solunda fonksiyon değerleri eksenin altında yer alır Öküz ve sağ üstte.
Fonksiyonun türevinin sıfır olduğu veya mevcut olmadığı bir fonksiyonun tanım kümesindeki bir argümanın değerlerine denir kritik noktalar.
Yukarıdakilerin hepsinden, fonksiyonun uç noktalarının kritik noktalar arasında olduğu sonucu çıkar, ancak her kritik nokta bir uç nokta değildir. Bu nedenle, bir fonksiyonun ekstremumunu bulmak için, fonksiyonun tüm kritik noktalarını bulmanız ve ardından bu noktaların her birini maksimum ve minimum için ayrı ayrı incelemeniz gerekir. Aşağıdaki teorem bu amaca hizmet eder.
Teorem 2. (Bir ekstremumun varlığı için yeterli koşul.) Fonksiyonun kritik noktayı içeren bir aralıkta sürekli olmasına izin verin X 0'dır ve bu aralığın tüm noktalarında türevlenebilirdir (belki de noktanın kendisi hariç) X 0). Bu noktadan soldan sağa doğru hareket edildiğinde türevin işareti artıdan eksiye değişirse, o zaman bu noktada X = X 0 fonksiyonunun maksimumu vardır. Eğer geçerken X Soldan sağa 0 ise türevin işareti eksiden artıya değişir, o zaman fonksiyonun bu noktada minimumu vardır.
Böylece eğer
Kanıt. Öncelikle şunu varsayalım ki geçerken X 0 türevin işareti artıdan eksiye değişir, yani. herkesin önünde X, noktaya yakın X 0 f "(x)> 0 için X< x 0 , f "(x)< 0 için x>x 0. Lagrange teoremini farka uygulayalım f(x) - f(x) 0 ) = f "(c)(x- x 0), nerede C arasında yatıyor X Ve X 0 .
Böylece tüm değerler için X yeterince yakın X 0 f(x)< f(x 0 ) . Ve bu şu anlama geliyor: o noktada X 0 fonksiyonunun maksimumu vardır.
Minimum teoremin ikinci kısmı da benzer şekilde kanıtlanır.
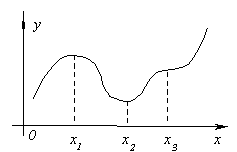
Bu teoremin anlamını şekilde açıklayalım. İzin vermek f "(x 1 ) =0 ve herhangi biri için X, yeterince yakın X 1, eşitsizlikler sağlandı
f "(x)< 0 saat X< x 1 , f "(x)> 0 saat x>x 1 .
Daha sonra noktanın solunda X 1 fonksiyon sağda artar ve azalır, bu nedenle X = X 1 fonksiyon artandan azalana doğru gider, yani maksimumu vardır.
Benzer şekilde noktaları da dikkate alabiliriz. X 2 ve X 3 .

Yukarıdakilerin tümü resimde şematik olarak gösterilebilir:
Ekstremum için y=f(x) fonksiyonunu inceleme kuralı
Örnekler. Minimum ve maksimum işlevleri keşfedin.
BİR FONKSİYONUN BİR BÖLÜM ÜZERİNDEKİ MAKSİMUM VE EN KÜÇÜK DEĞERLERİ
En büyüğü Bir fonksiyonun bir aralıktaki değeri, bu aralıktaki tüm değerlerinin en büyüğüdür ve en küçük– tüm değerlerinin en küçüğü.
İşlevi düşünün Fonksiyona izin ver segmentte sürekli [ a, b] Bilindiği gibi böyle bir fonksiyon maksimum ve minimum değerlerine parçanın sınırında veya içinde ulaşır. Bir fonksiyonun en büyük veya en küçük değerine parçanın iç noktasında ulaşılıyorsa bu değer, fonksiyonun maksimum veya minimum değeridir, yani kritik noktalarda elde edilir.
Böylece aşağıdakileri elde ederiz bir segmentteki bir fonksiyonun en büyük ve en küçük değerlerini bulma kuralı[ a, b] :
Bir fonksiyonun artan, azalan ve ekstremum değerleri
Bir fonksiyonun artış, azalma ve ekstremum aralıklarını bulmak hem bağımsız bir görevdir hem de diğer görevlerin önemli bir parçasıdır. tam fonksiyon çalışması. Fonksiyonun artış, azalış ve ekstremum değerlerine ilişkin ilk bilgiler aşağıda verilmiştir. türev üzerine teorik bölümÖn çalışma için şiddetle tavsiye ettiğim (veya tekrarlama)– ayrıca aşağıdaki materyalin aynı temele dayanması nedeniyle esasen türev, bu makalenin uyumlu bir devamı niteliğindedir. Bununla birlikte, eğer zaman kısaysa, o zaman bugünkü dersten alınan örneklerin tamamen resmi bir uygulaması da mümkündür.
Ve bugün havada nadir görülen bir birlik ruhu var ve orada bulunan herkesin arzuyla yandığını doğrudan hissedebiliyorum. Türevini kullanarak bir fonksiyonu keşfetmeyi öğrenin. Bu nedenle makul, iyi, ebedi terminoloji hemen monitör ekranlarınızda belirir.
Ne için? Sebeplerden biri en pratik olanıdır: böylece belirli bir görevde genel olarak sizden ne istendiğinin netleşmesi için!
Fonksiyonun monotonluğu. Bir fonksiyonun ekstremum noktaları ve ekstremumları
Biraz fonksiyon düşünelim. Basitçe söylemek gerekirse, onun olduğunu varsayıyoruz. sürekli tüm sayı doğrusunda:

Her ihtimale karşı, özellikle yeni tanışan okuyucular için olası yanılsamalardan bir an önce kurtulalım. fonksiyonun sabit işaret aralıkları. Şimdi biz İLGİLİ DEĞİL, fonksiyonun grafiğinin eksene göre nasıl yerleştirildiği (eksenin kesiştiği yerde yukarıda, aşağıda). İkna edici olmak için eksenleri zihinsel olarak silin ve bir grafik bırakın. Çünkü ilginin yattığı yer burası.
İşlev artar Bir aralıkta, bu aralığın ilişkiyle birbirine bağlanan herhangi iki noktası için eşitsizlik doğrudur. Yani, argümanın daha büyük bir değeri, fonksiyonun daha büyük bir değerine karşılık gelir ve grafiği "aşağıdan yukarıya" doğru gider. Gösterim işlevi aralık boyunca büyür.
Aynı şekilde, fonksiyon azalır Belirli bir aralığın herhangi iki noktası için eşitsizlik doğru olacak şekilde bir aralıkta. Yani, argümanın daha büyük bir değeri, fonksiyonun daha küçük bir değerine karşılık gelir ve grafiği "yukarıdan aşağıya" doğru gider. Fonksiyonumuz aralıklarla azalır ![]() .
.
Bir fonksiyon belirli bir aralıkta artıyor veya azalıyorsa buna denir. Kesinlikle monoton bu aralıkta. Monotonluk nedir? Kelimenin tam anlamıyla alın – monotonluk.
Ayrıca tanımlayabilirsiniz azalmayan işlev (ilk tanımda rahat durum) ve artmayan fonksiyon (2. tanımda yumuşatılmış durum). Bir aralıkta azalmayan veya artmayan bir fonksiyona, belirli bir aralıkta monoton fonksiyon denir (katı monotonluk, “basitçe” monotonluğun özel bir durumudur).
Teori aynı zamanda yarım aralıklar, bölümler de dahil olmak üzere bir fonksiyonun artışını/azalışını belirlemeye yönelik diğer yaklaşımları da dikkate alır, ancak başınıza yağ-yağ-yağ dökmemek için kategorik tanımlarla açık aralıklarla çalışmayı kabul edeceğiz. - bu daha açık ve birçok pratik sorunu çözmek için oldukça yeterli.
Böylece, makalelerimde "bir fonksiyonun monotonluğu" ifadesi neredeyse her zaman gizlenecek aralıklar katı monotonluk(kesinlikle artan veya kesinlikle azalan fonksiyon).
Bir noktanın mahallesi. Ardından öğrencilerin bulabildikleri her yere kaçtıkları ve köşelerde dehşet içinde saklandıkları sözler. ...her ne kadar gönderiden sonra Cauchy sınırları Muhtemelen artık saklanmıyorlar, sadece hafifçe titriyorlar =) Endişelenmeyin, artık matematiksel analiz teoremlerinin kanıtı olmayacak - tanımları daha kesin bir şekilde formüle etmek için çevreye ihtiyacım vardı ekstrem noktalar. Hatırlayalım:
Bir noktanın mahallesi Belirli bir noktayı içeren bir aralık denir ve kolaylık sağlamak için aralığın genellikle simetrik olduğu varsayılır. Örneğin bir nokta ve onun standart komşuluğu:
Aslında tanımlar:
Nokta denir kesin maksimum nokta, Eğer var onun mahallesi, herkes için değerleri, noktanın kendisi dışında eşitsizliktir. Özel örneğimizde bu bir noktadır.
Nokta denir kesin minimum nokta, Eğer var onun mahallesi, herkes için değerleri, noktanın kendisi dışında eşitsizliktir. Çizimde “a” noktası var.
Not : Komşuluk simetrisi gerekliliği hiç de gerekli değildir. Ayrıca önemli varoluşun gerçeği belirtilen koşulları karşılayan mahalle (küçük veya mikroskobik)
Noktalara denir kesinlikle ekstremum noktalar ya da sadece ekstrem noktalar işlevler. Yani maksimum puanlar ve minimum puanlar için genelleştirilmiş bir terimdir.
“Aşırı” kelimesini nasıl anlıyoruz? Evet, monotonluk kadar doğrudan. Hız trenlerinin uç noktaları.
Monotonluk durumunda olduğu gibi, gevşek varsayımlar mevcuttur ve teoride daha da yaygındır. (tabii ki, dikkate alınan katı davalar da bu kapsamdadır!):
Nokta denir maksimum nokta, Eğer varçevresi öyle herkes için
Nokta denir minimum puan, Eğer varçevresi öyle herkes için Bu mahallenin değerleri, eşitsizliği barındırıyor.
Son iki tanıma göre, sabit bir fonksiyonun (veya bir fonksiyonun "düz bölümünün") herhangi bir noktasının hem maksimum hem de minimum nokta olarak kabul edildiğini unutmayın! Bu arada fonksiyon hem artmayan hem de azalmayan, yani monotondur. Bununla birlikte, bu düşünceleri teorisyenlere bırakacağız, çünkü pratikte neredeyse her zaman geleneksel "tepeler" ve "oyuklar" (çizime bakınız) benzersiz bir "tepenin kralı" veya "bataklığın prensesi" ile düşünürüz. Bir çeşitlilik olarak ortaya çıkar uç, yukarı veya aşağı yönlendirilmiş, örneğin noktadaki fonksiyonun minimumu.
Ah, kraliyetten bahsetmişken:
– anlamı denir maksimum işlevler;
– anlamı denir minimum işlevler.
Ortak ad – aşırılıklar işlevler.
Lütfen sözlerinize dikkat edin!
Ekstrem noktalar– bunlar “X” değerleridir.
Aşırılıklar– “oyun” anlamları.
! Not : Bazen listelenen terimler doğrudan fonksiyonun KENDİSİNİN GRAFİĞİ üzerinde yer alan “X-Y” noktalarına atıfta bulunur.
Bir fonksiyon kaç ekstrema sahip olabilir?
Yok, 1, 2, 3,... vb. sonsuza dek. Örneğin sinüsün sonsuz sayıda minimum ve maksimum değeri vardır.
ÖNEMLİ!"Maksimum fonksiyon" terimi aynı değil"bir fonksiyonun maksimum değeri" terimi. Değerin yalnızca yerel bir mahallede maksimum olduğunu ve sol üstte "daha havalı yoldaşların" bulunduğunu fark etmek kolaydır. Aynı şekilde “bir fonksiyonun minimumu” ile “bir fonksiyonun minimum değeri” aynı değildir ve çizimde değerin sadece belirli bir alanda minimum olduğunu görüyoruz. Bu bakımdan ekstremum noktalara da denir. yerel ekstremum noktaları ve ekstremum – yerel aşırılıklar. Yakınlarda yürürler ve dolaşırlar ve küresel kardeşler. Yani herhangi bir parabolün tepe noktasında küresel minimum veya küresel maksimum. Ayrıca, aşırı uç türleri arasında ayrım yapmayacağım ve açıklama daha çok genel eğitim amaçlı olarak dile getirildi - "yerel"/"küresel" ek sıfatları sizi şaşırtmamalı.
Teoriye yaptığımız kısa geziyi bir deneme çekimiyle özetleyelim: "Fonksiyonun monotonluk aralıklarını ve ekstremum noktalarını bulma" görevi ne anlama geliyor?
İfade sizi şunu bulmaya teşvik ediyor:
– artan/azalan fonksiyon aralıkları (azalmayan, artmayan çok daha az sıklıkla görülür);
– maksimum ve/veya minimum puanlar (varsa). Başarısızlığı önlemek için minimum/maksimum değerleri kendiniz bulmak daha iyidir ;-)
Bütün bunlar nasıl belirlenir? Türev fonksiyonunu kullanma!
Artan, azalan aralıklar nasıl bulunur?
Fonksiyonun ekstrem noktaları ve ekstremumları?
Aslında pek çok kural zaten biliniyor ve anlaşılıyor. türevin anlamı hakkında ders.
Teğet türev ![]() boyunca fonksiyonun arttığına dair sevindirici bir haber getiriyor tanım alanı.
boyunca fonksiyonun arttığına dair sevindirici bir haber getiriyor tanım alanı.
Kotanjant ve türevi ile ![]() durum tam tersidir.
durum tam tersidir.
Ark sinüs aralık boyunca artar - buradaki türev pozitiftir: ![]() .
.
Fonksiyon tanımlı ancak türevlenebilir olmadığında. Ancak kritik noktada sağdan türev ve sağdan teğet vardır, diğer kenarda ise bunların solak karşılıkları vardır.
Ark kosinüs ve türevi için de benzer akıl yürütmenin sizin için çok zor olmayacağını düşünüyorum.
Yukarıdaki durumların tümü, bunların çoğu tablosal türevler, hatırlatırım, doğrudan şuradan takip edin türev tanımları.
Neden bir fonksiyonu türevini kullanarak araştıralım?
Bu fonksiyonun grafiğinin neye benzediğini daha iyi anlamak için: "aşağıdan yukarıya" gittiği yer, "yukarıdan aşağıya" gittiği yer, minimum ve maksimumlara ulaştığı yer (eğer ulaşıyorsa). Tüm fonksiyonlar o kadar basit değildir; çoğu durumda belirli bir fonksiyonun grafiği hakkında hiçbir fikrimiz yoktur.
Daha anlamlı örneklere geçmenin ve düşünmenin zamanı geldi Bir fonksiyonun monotonluk ve ekstremum aralıklarını bulmak için algoritma:
Örnek 1
Fonksiyonun artış/azalış aralıklarını ve ekstremumlarını bulun
![]()
Çözüm:
1) İlk adım bulmaktır bir fonksiyonun alanı ve ayrıca kesme noktalarını (varsa) not edin. Bu durumda fonksiyon tüm sayı doğrusunda süreklidir ve bu eylem bir dereceye kadar resmidir. Ancak bazı durumlarda burada ciddi tutkular alevlenir, bu yüzden paragrafı küçümsemeden ele alalım.
2) Algoritmanın ikinci noktası şundan kaynaklanmaktadır:
bir ekstremum için gerekli koşul:
Bir noktada bir ekstremum varsa o zaman değer de mevcut değildir.
Sonu kafanız mı karıştı? “Modül x” fonksiyonunun ekstremumu .
Şart gerekli ama yeterli değil ve bunun tersi her zaman doğru değildir. Dolayısıyla eşitlikten fonksiyonun noktasında maksimum veya minimuma ulaştığı sonucu henüz çıkmaz. Yukarıda klasik bir örnek zaten vurgulanmıştı - bu kübik bir parabol ve onun kritik noktasıdır.
Ancak öyle de olsa, bir ekstremum için gerekli koşul, şüpheli noktaların bulunması ihtiyacını zorunlu kılmaktadır. Bunu yapmak için türevi bulun ve denklemi çözün:
İlk makalenin başında fonksiyon grafikleri hakkında Bir örnek kullanarak hızlı bir şekilde parabolün nasıl oluşturulacağını anlattım. ![]() : “...birinci türevi alıp sıfıra eşitliyoruz: ...Yani denklemimizin çözümü: - parabolün tepe noktası tam da bu noktada...”. Sanırım artık herkes parabolün tepe noktasının neden tam olarak bu noktada bulunduğunu anladı =) Genel olarak burada da benzer bir örnekle başlamalıyız ama bu çok basit (bir çaydanlık için bile). Ayrıca dersin en sonunda bir analog var. bir fonksiyonun türevi. Bu nedenle dereceyi artıralım:
: “...birinci türevi alıp sıfıra eşitliyoruz: ...Yani denklemimizin çözümü: - parabolün tepe noktası tam da bu noktada...”. Sanırım artık herkes parabolün tepe noktasının neden tam olarak bu noktada bulunduğunu anladı =) Genel olarak burada da benzer bir örnekle başlamalıyız ama bu çok basit (bir çaydanlık için bile). Ayrıca dersin en sonunda bir analog var. bir fonksiyonun türevi. Bu nedenle dereceyi artıralım:
Örnek 2
Fonksiyonun monotonluk ve ekstremum aralıklarını bulun
Bu kendi başınıza çözebileceğiniz bir örnektir. Dersin sonunda tam bir çözüm ve problemin yaklaşık nihai örneği.
Kesirli-rasyonel fonksiyonlarla uzun zamandır beklenen buluşma anı geldi:
Örnek 3
Birinci türevi kullanarak bir fonksiyonu keşfedin
Lütfen aynı görevin ne kadar çeşitli şekillerde yeniden formüle edilebileceğine dikkat edin.
Çözüm:
1) Fonksiyon noktalarda sonsuz süreksizliklere maruz kalır.
2) Kritik noktaları tespit ediyoruz. Birinci türevi bulup sıfıra eşitleyelim: 
Denklemi çözelim. Payı sıfır olduğunda bir kesir sıfırdır:
Böylece üç kritik nokta elde ediyoruz: ![]()
3) Tespit edilen TÜM noktaları sayı doğrusu üzerinde çizeriz ve aralık yöntemi TÜREVİN işaretlerini tanımlarız:
Aralıkta bir nokta alıp türevin değerini hesaplamanız gerektiğini size hatırlatırım. ![]() ve işaretini belirleyin. Saymak bile değil, sözlü olarak "tahmin etmek" daha karlı. Örneğin aralığa ait bir noktayı alalım ve yerine koyma işlemini gerçekleştirelim:
ve işaretini belirleyin. Saymak bile değil, sözlü olarak "tahmin etmek" daha karlı. Örneğin aralığa ait bir noktayı alalım ve yerine koyma işlemini gerçekleştirelim: ![]() .
. 
Dolayısıyla iki "artı" ve bir "eksi" bir "eksi" verir, bu da türevin tüm aralık boyunca negatif olduğu anlamına gelir.
Anladığınız gibi eylemin altı aralığın her biri için gerçekleştirilmesi gerekiyor. Bu arada, pay faktörünün ve paydanın herhangi bir aralıktaki herhangi bir nokta için kesinlikle pozitif olduğunu ve bunun görevi büyük ölçüde basitleştirdiğini unutmayın.
Yani türev bize FONKSİYONUN KENDİSİNİN şu kadar arttığını söyledi: ![]() ve kadar azalır. Birleştir simgesiyle aynı türdeki aralıkları birleştirmek uygundur.
ve kadar azalır. Birleştir simgesiyle aynı türdeki aralıkları birleştirmek uygundur.
Fonksiyonun maksimuma ulaştığı noktada:
Fonksiyonun minimuma ulaştığı noktada: ![]()
İkinci değeri neden yeniden hesaplamak zorunda olmadığınızı düşünün ;-)
Bir noktadan geçerken türev işaret değiştirmez, dolayısıyla fonksiyonun orada EKSTREMİ YOKTUR - hem azaldı hem de azalan kaldı.
! Önemli bir noktayı tekrarlayalım: noktalar kritik olarak kabul edilmez - bir işlev içerirler tanımlanmamış. Buna göre burada Prensipte hiçbir aşırılık olamaz(türev işaret değiştirse bile).
Cevap: fonksiyon şu kadar artar: ![]() ve azalır Fonksiyonun maksimum değerine ulaşıldığı noktada:
ve azalır Fonksiyonun maksimum değerine ulaşıldığı noktada: ![]() , ve bu noktada – minimum: .
, ve bu noktada – minimum: .
Monotonluk aralıkları ve ekstremum bilgisi, yerleşik bilgilerle birlikte asimptotlar zaten fonksiyon grafiğinin görünümü hakkında çok iyi bir fikir veriyor. Ortalama eğitime sahip bir kişi, bir fonksiyonun grafiğinin iki dikey asimptotu ve bir eğik asimptotu olduğunu sözlü olarak belirleyebilir. İşte kahramanımız: 
Çalışmanın sonuçlarını bu fonksiyonun grafiğiyle ilişkilendirmeyi bir kez daha deneyin.
Kritik noktada ekstremum yoktur ancak dönüm noktası(kural olarak benzer durumlarda olur).
Örnek 4
Fonksiyonun ekstremumunu bulun
Örnek 5
Fonksiyonun monotonluk aralıklarını, maksimumlarını ve minimumlarını bulun
…bugün neredeyse bir nevi “küpün içindeki X” tatiline benziyor....
Soooo, galeride kim bunun için içki içmeyi teklif etti? =)
Her görevin kendine özgü nüansları ve teknik incelikleri vardır ve bunlar dersin sonunda yorumlanır.
Fonksiyonlar, birinci ve ikinci türevlerin varlığını bilmek ve fiziksel anlamlarını anlamak hiç de gerekli değildir. Öncelikle aşağıdakileri anlamanız gerekir:
- fonksiyonun ekstremumları, keyfi olarak küçük bir komşulukta fonksiyonun değerini maksimuma çıkarır veya tersine minimuma indirir;
- uç noktada fonksiyonda herhangi bir süreksizlik olmamalıdır.
Ve şimdi aynı şey, yalnızca basit bir dilde. Tükenmez kalemin ucuna bakın. Kalem, yazı ucu yukarı bakacak şekilde dikey olarak konumlandırılırsa, topun en ortası en uç nokta, yani en yüksek nokta olacaktır. Bu durumda maksimumdan bahsediyoruz. Şimdi kalemi yazı ucu aşağı bakacak şekilde çevirirseniz, topun ortasında zaten minimum bir işlev olacaktır. Burada verilen şekli kullanarak kırtasiye kalemi için listelenen manipülasyonları hayal edebilirsiniz. Yani bir fonksiyonun ekstremumları her zaman kritik noktalardır: Maksimum veya minimum. Grafiğin bitişik bölümü istenildiği kadar keskin veya pürüzsüz olabilir, ancak her iki tarafta da mevcut olması gerekir, ancak bu durumda nokta bir ekstremumdur. Grafik yalnızca bir tarafta mevcutsa, bir tarafta ekstremum koşulları sağlansa bile bu nokta ekstremum olmayacaktır. Şimdi fonksiyonun ekstremumlarını bilimsel açıdan inceleyelim. Bir noktanın ekstremum olarak kabul edilebilmesi için aşağıdaki koşulların sağlanması gerekli ve yeterlidir:
- birinci türev sıfırdı veya o noktada mevcut değildi;
- Bu noktada birinci türevin işareti değişti.

Bu durum, yüksek dereceli türevlerin bakış açısından biraz farklı yorumlanır: bir noktada türevlenebilen bir fonksiyon için, sıfıra eşit olmayan tek sıralı bir türevin olması yeterlidir, ancak tüm düşük dereceli türevlerin mevcut olması gerekir. ve sıfıra eşit olsun. Bu, ders kitaplarındaki teoremlerin mümkün olan en basit yorumudur. Ancak en sıradan insanlar için bu noktayı bir örnekle açıklamaya değer. Temel sıradan bir paraboldür. Hemen rezervasyon yapalım: Sıfır noktasında minimum var. Sadece küçük bir matematik:
- birinci türev (X 2) | = 2X, sıfır noktası için 2X = 0;
- ikinci türev (2X) | = 2, sıfır noktası için 2 = 2.

Bu basit şekilde, hem birinci dereceden hem de yüksek dereceden türevler için fonksiyonun ekstremumunu belirleyen koşullar gösterilmektedir. Buna, ikinci türevin, yukarıda tartışıldığı gibi, sıfıra eşit olmayan tek sıralı tam olarak aynı türev olduğunu ekleyebiliriz. İki değişkenli bir fonksiyonun ekstremumları söz konusu olduğunda, her iki argüman için de koşulların karşılanması gerekir. Genelleme yapıldığında kısmi türevler kullanılır. Yani bir noktada bir ekstremun varlığı için birinci dereceden türevlerin her ikisinin de sıfıra eşit olması veya bunlardan en az birinin bulunmaması gerekir. Bir ekstremun varlığının yeterli olduğundan emin olmak için, ikinci dereceden türevlerin çarpımı ile fonksiyonun karışık ikinci dereceden türevinin karesi arasındaki fark olan bir ifade incelenir. Bu ifade sıfırdan büyükse bir ekstremum var demektir, ancak sıfıra eşitse soru açık kalır ve ek araştırmaların yapılması gerekir.