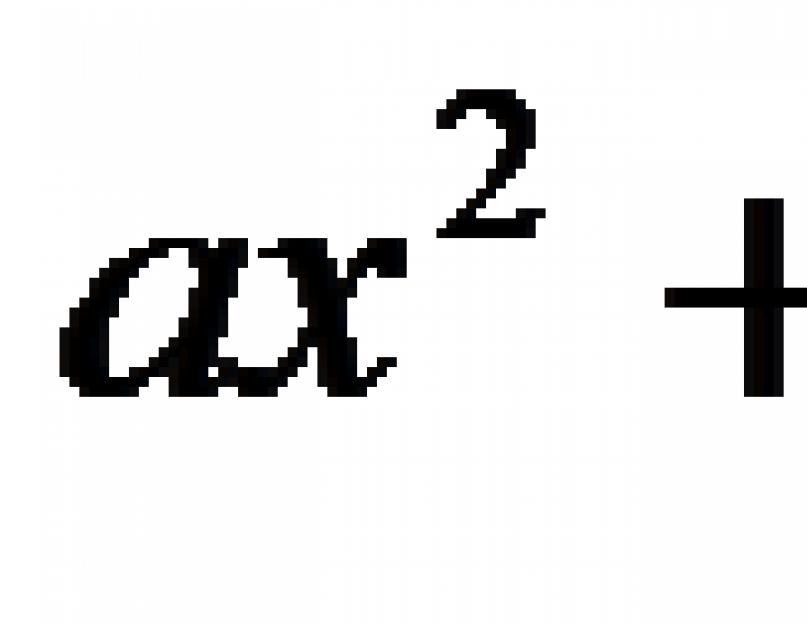Araştırma çalışması
konuyla ilgili
"Çözüm yolları ikinci dereceden denklemler »
Gerçekleştirilen:
grup 8 "G" sınıfı
İş yöneticisi:
Benkovskaya Maria Mihaylovna
Projenin amaç ve hedefleri.
1. Diğer bilimler gibi matematiğin de yeterince çözülmemiş gizemi olduğunu gösterin.
2. Matematikçilerin standart olmayan düşünce ile ayırt edildiğini vurgulayın. Ve bazen zeka ve sezgi iyi matematikçi sadece şaşırtıcı!
3. İkinci dereceden denklemleri çözme girişiminin, matematikte yeni kavram ve fikirlerin geliştirilmesine katkıda bulunduğunu gösterin.
4. Çeşitli bilgi kaynaklarıyla çalışmayı öğrenin.
5. Devam et Araştırma çalışması matematik
Araştırma aşamaları
1. İkinci dereceden denklemlerin ortaya çıkış tarihi.
2. İkinci dereceden bir denklemin tanımı ve türleri.
3. İkinci dereceden denklemleri diskriminant formülünü kullanarak çözme.
4. Francois Viet ve teoremi.
5. İkinci dereceden bir denklemin köklerini hızlı bir şekilde bulmak için katsayıların özellikleri.
6. Pratik yönlendirme.
Denklemler, teoremler aracılığıyla
Bir çok sorunu çözdüm.
(Chaucer, İngiliz şair, orta Çağlar.)
sahne. İkinci dereceden denklemlerin ortaya çıkış tarihi.
Sadece birinci değil, aynı zamanda ikinci dereceden denklemleri antik çağda çözme ihtiyacı, alanları bulma ile ilgili problemleri çözme ihtiyacından kaynaklandı. araziler ve askeri nitelikteki toprak işleri ile astronomi ve matematiğin kendisinin gelişimi.
Babilliler, MÖ 2000 civarında ikinci dereceden denklemleri çözebildiler. Babil metinlerinde belirtilen bu denklemleri çözme kuralı, esasen modern olanlarla örtüşmektedir, ancak Babillilerin kuralı nasıl buldukları bilinmemektedir. Şimdiye kadar bulunan hemen hemen tüm çiviyazılı metinler, nasıl bulunduklarına dair hiçbir belirti olmaksızın, yalnızca tarifler şeklinde belirtilen çözümlerle ilgili sorunları verir.
Karşın yüksek seviye Babil'de cebirin gelişimi, çivi yazılı metinlerde negatif sayı kavramı ve ikinci dereceden denklemleri çözmek için genel yöntemler yoktur.
Diophantus'un "Aritmetiği", açıklamaların eşlik ettiği ve denklemleri formüle ederek çözülen sistematik bir dizi problem içerir. çeşitli dereceler, ancak cebirin sistematik bir anlatımından yoksundur.
İkinci dereceden denklemler için problemler, 499'da derlenen astronomik incelemeler "Aryabhattiam" da zaten bulundu. Hintli matematikçi ve astronom Aryabhatta. Başka bir Hintli bilgin Brahmagupta (7. yüzyıl), Genel kural tek bir kanonik forma indirgenmiş ikinci dereceden denklemlerin çözümleri:
Al-Khorezmi'nin cebirsel incelemesi, doğrusal ve ikinci dereceden denklemlerin bir sınıflandırmasını verir. Yazarın 6 tür denklemi vardır. bilmeyen el-Harezmi için negatif sayılar, her denklemin terimleri, çıkarmalar değil, toplamalardır. Aynı zamanda, pozitif çözümleri olmayan denklemler kasıtlı olarak dikkate alınmaz; eksik bir ikinci dereceden denklemi çözerken, el-Harezmi, 17. yüzyıldan önceki tüm bilim adamları gibi, sıfır çözümü dikkate almaz.
El-Harezmi'nin incelemesi, ikinci dereceden denklemlerin sınıflandırılmasının ve çözümleri için formüllerin sistematik olarak sunulduğu, bize ulaşan ilk kitaptır.
Avrupa'daki el-Harezmi modeli üzerinde ikinci dereceden denklemleri çözmek için formüller ilk olarak 1202'de İtalyan matematikçi Leonardo Fibonacci tarafından yazılan Abaküs Kitabı'nda ortaya kondu. Bu hacimli eser, sunumun bütünlüğü ve netliği ile ayırt edilir. Yazar bağımsız olarak problemleri çözmek için bazı yeni cebirsel yöntemler geliştirdi ve Avrupa'da negatif sayıların kullanılmasına ilk yaklaşan kişi oldu. Kitabı cebirsel bilginin sadece İtalya'da değil, Almanya, Fransa ve diğer Avrupa ülkelerinde de yayılmasına katkıda bulundu. Abaküs Kitabı'ndaki pek çok sorun, 16.-17. ve kısmen 18. yüzyılların neredeyse tüm Avrupa ders kitaplarına geçti.
Tek bir kanonik forma indirgenmiş ikinci dereceden denklemleri çözmek için genel kural  tüm olası işaret kombinasyonları ile katsayılar b,c Avrupa'da sadece 1544'te M. Stiefel tarafından formüle edilmiştir.
tüm olası işaret kombinasyonları ile katsayılar b,c Avrupa'da sadece 1544'te M. Stiefel tarafından formüle edilmiştir.
İkinci dereceden bir denklemi çözmek için formülün türetilmesi Genel görünüm Viet vardır, ancak Viet yalnızca pozitif kökleri tanımıştır. İtalyan matematikçiler Tartaglia, Cardano, Bombelli, 16. yüzyılda sadece olumlu değil, aynı zamanda olumsuz kökleri de hesaba katan ilk kişiler arasındaydı. Sadece 17. yüzyılda Girrard, Descartes, Newton ve diğer bilim adamlarının çalışmaları sayesinde ikinci dereceden denklemleri çözme yöntemi modern bir biçim aldı.

ÇIKIŞ:
İkinci dereceden denklemlerle ilgili problemler 499'da zaten bulundu.
AT eski hindistan zor sorunları çözmede halka açık yarışmalar dağıtıldı - OLYMPIADS .
©2015-2019 sitesi
Tüm hakları yazarlarına aittir. Bu site yazarlık iddiasında bulunmaz, ancak ücretsiz kullanım sağlar.
Sayfa oluşturma tarihi: 2016-04-11
Çeşitli medeniyetlerin temsilcileri: Antik Mısır, Eski Babil, Antik Yunan, Eski Hindistan, Antik Çin, Ortaçağ Doğu, Avrupa ikinci dereceden denklemleri çözme tekniklerinde ustalaştı.
İlk kez, Eski Mısır matematikçileri ikinci dereceden bir denklemi çözebildiler. Matematiksel papirüslerden biri şu sorunu içeriyor:
"Alanı 12 ise ve - uzunlukları genişliğe eşitse, dikdörtgen şeklindeki bir alanın kenarlarını bulun." Papirüs, "Alanın uzunluğu 4'tür" diyor.
Bin yıl geçti, negatif sayılar cebire girdi. x² = 16 denklemini çözerek iki sayı elde ederiz: 4, -4.
Tabii ki Mısır probleminde alanın uzunluğu sadece pozitif bir değer olabileceğinden X = 4 alırdık.
Bize ulaşan kaynaklar, antik bilim adamlarının bilinmeyen nicelikleri olan problemleri çözmek için bazı genel yöntemlere sahip olduklarını göstermektedir. İkinci dereceden denklemleri çözmek için Babil metinlerinde ortaya konan kural, esasen modern olanla aynıdır, ancak Babillilerin "bu noktaya nasıl geldikleri" bilinmemektedir. Ancak bulunan hemen hemen tüm papirüs ve çiviyazılı metinlerde sadece çözümleriyle ilgili problemlere yer verilmiştir. Yazarlar sadece ara sıra sayısal hesaplamalarını “Bak!”, “Yap!”, “Doğru buldunuz!” gibi ortalama yorumlarla sağladılar.
Yunan matematikçi Diophantus, ikinci dereceden denklemleri yazdı ve çözdü. Onun "Aritmetiği" cebirin sistematik bir sunumunu içermez, ancak açıklamaların eşlik ettiği ve çeşitli derecelerde denklemlerin derlenmesiyle çözülen sistematik bir dizi problem içerir.
İkinci dereceden denklemlerin derlenmesi için görevler, Hintli matematikçi ve astronom Ariabhatta tarafından 499'da derlenen astronomik tez "Aria-bhatiam" da zaten bulunur.
Başka bir Hintli bilim adamı Brahmagupta (7. yüzyıl), ax² + bx = c biçimindeki ikinci dereceden denklemleri çözmek için genel kuralı özetledi.
Eski Hindistan'da, zor sorunları çözmede halka açık yarışmalar yaygındı. Bu tür yarışmalarla ilgili eski Hint kitaplarından birinde şöyle denir: “Güneş parlaklığıyla yıldızları nasıl gölgede bırakıyorsa, o kadar bilim adamı Cebirsel problemleri önererek ve çözerek, halka açık toplantılarda bir başkasının ihtişamını gölgede bırakın. Görevler genellikle şiirsel biçimde giyinirdi.
İşte XII.Yüzyılın ünlü Hintli matematikçisinin sorunlarından biri. Bhaskara:
frisky maymun sürüsü
İyi yemek, eğlenmek.
Meydandaki sekizinci kısmı açıklıkta eğlendi.
Ve asmalar boyunca on iki ... zıplamaya, asılı kalmaya başladı ...
kaç maymun vardı
Bana bu sürüde mi söylüyorsun?
Bhaskara'nın çözümü, ikinci dereceden denklemlerin köklerinin iki değerliliğini bildiğini gösteriyor.
Bize ulaşan en eski Çin matematik metinleri, MÖ 1. yüzyılın sonuna kadar uzanıyor. M.Ö. II. Yüzyılda. M.Ö. Dokuz Kitapta Matematik yazıldı. Daha sonra, 7. yüzyılda, yüzyıllarca çalışılan "On Klasik Risale" koleksiyonuna dahil edildi. "Dokuz Kitapta Matematik" incelemesi, iki sayının toplamının karesi formülünü kullanarak karekökün nasıl çıkarılacağını açıklar.
Yöntem, Çinlilerin bilinmeyen bir miktarı ifade ettiği için "tian-yuan" (kelimenin tam anlamıyla - "göksel öğe") olarak adlandırıldı.
Yaygın olarak bilinen sorunları çözmeye yönelik ilk rehber, 9. yüzyılın Bağdat âliminin eseriydi. Muhammed bin Musa el Harezmi. "El-jabr" kelimesi - zamanla iyi bilinen "cebir" kelimesine dönüştü ve el-Harezmi'nin bileşiminin kendisi oldu. Başlangıç noktası denklem çözme biliminin geliştirilmesinde. Al-Khorezmi'nin cebirsel incelemesi, doğrusal ve ikinci dereceden denklemlerin bir sınıflandırmasını verir. Yazar, bunları aşağıdaki gibi ifade ederek altı tür denklemi listeler:
-kareler eşit kökler, bu ah ² = bx;
-kareler eşit sayı, bu ah ² = c;
-kökler sayıya eşittir, yani, ax = c;
-kareler ve sayılar köklere eşittir, bu ah ²+ c \u003d bx;
-kareler ve kökler sayıya eşittir, bu ah ² + bx \u003d c;
-kökler ve sayılar karedir, yani bx + c = balta ²;
El-Harezmi'nin incelemesi, ikinci dereceden denklemlerin sınıflandırılmasının sistematik olarak sunulduğu ve çözüm formüllerinin verildiği bize ulaşan ilk kitaptır.
Avrupa'daki el-Harezmi modeli üzerinde ikinci dereceden denklemleri çözmek için formüller ilk olarak 1202'de İtalyan matematikçi Leonardo Fibonacci tarafından yazılan Abaküs Kitabı'nda ortaya kondu. Yazar bağımsız olarak bazı yeni cebirsel problem çözme örnekleri geliştirdi ve Avrupa'da negatif sayıların kullanılmasına ilk yaklaşan kişi oldu. Kitabı cebirsel bilginin sadece İtalya'da değil, Almanya, Fransa ve diğer Avrupa ülkelerinde de yayılmasına katkıda bulundu. Abaküs Kitabından birçok görev, 16.-17. yüzyılların neredeyse tüm Avrupa ders kitaplarında yer aldı. ve 18. yüzyılın bir parçası.
Tek bir kanonik forma indirgenmiş ikinci dereceden denklemleri çözmek için genel kural x ² + bx \u003d c, b ve c katsayılarının olası tüm işaret kombinasyonları ile Avrupa'da sadece 1544'te M. Stiefel tarafından formüle edilmiştir.
Vieta, ikinci dereceden bir denklemi çözmek için formülün genel bir türevine sahiptir, ancak aynı zamanda yalnızca pozitif kökleri de tanımıştır. İtalyan matematikçiler Tartaglia, Cardano, Bombelli, 16. yüzyılda ilk olanlar arasındaydı. pozitif ve negatif köklere ek olarak dikkate alın. Sadece 17. yüzyılda Girard, Descartes, Newton ve diğer bilim adamlarının çalışmaları sayesinde ikinci dereceden denklemleri çözme yöntemi modern bir biçim aldı.
Kopyevskaya kırsal orta öğretim okulu
İkinci Dereceden Denklemleri Çözmenin 10 Yolu
Başkan: Patrikeeva Galina Anatolyevna,
matematik öğretmeni
s.Kopyevo, 2007
1. İkinci dereceden denklemlerin gelişim tarihi
1.1 Eski Babil'de ikinci dereceden denklemler
1.2 Diophantus ikinci dereceden denklemleri nasıl derledi ve çözdü?
1.3 Hindistan'da ikinci dereceden denklemler
1.4 Harezmi'deki ikinci dereceden denklemler
1.5 Avrupa XIII - XVII yüzyıllarda ikinci dereceden denklemler
1.6 Vieta teoremi hakkında
2. İkinci dereceden denklemleri çözme yöntemleri
Çözüm
Edebiyat
1. İkinci dereceden denklemlerin gelişim tarihi
1.1 Eski Babil'de ikinci dereceden denklemler
Eski zamanlarda sadece birinci değil, aynı zamanda ikinci dereceden denklemleri çözme ihtiyacı, askeri nitelikteki arazi ve toprak işlerinin yanı sıra astronomi ve bilimin gelişmesiyle ilgili sorunları çözme ihtiyacından kaynaklandı. matematiğin kendisi. İkinci dereceden denklemler yaklaşık MÖ 2000'i çözebildi. e. Babilliler.
Modern cebirsel gösterimi uygulayarak, çivi yazısı metinlerinde eksik olanlara ek olarak, örneğin tam ikinci dereceden denklemler olduğunu söyleyebiliriz:
X 2 + X = ¾; X 2 - X = 14,5
Babil metinlerinde geçen bu denklemleri çözme kuralı, esasen modern olanla örtüşmektedir, ancak Babillilerin bu kurala nasıl geldikleri bilinmemektedir. Şimdiye kadar bulunan hemen hemen tüm çiviyazılı metinler, nasıl bulunduklarına dair hiçbir belirti olmaksızın, yalnızca tarifler şeklinde belirtilen çözümlerle ilgili sorunları verir.
Babil'de cebirin yüksek düzeyde gelişmesine rağmen, çivi yazılı metinler negatif sayı kavramından ve ikinci dereceden denklemleri çözmek için genel yöntemlerden yoksundur.
1.2 Diophantus ikinci dereceden denklemleri nasıl derler ve çözer.
Diophantus' Aritmetiği, cebirin sistematik bir açıklamasını içermez, ancak açıklamaların eşlik ettiği ve çeşitli derecelerde denklemler kurarak çözülen sistematik bir dizi problem içerir.
Diophantus denklemleri derlerken çözümü basitleştirmek için bilinmeyenleri ustaca seçer.
Burada, örneğin, görevlerinden biri.
Görev 11."Toplamlarının 20 ve çarpımlarının 96 olduğunu bilerek iki sayı bulun"
Diophantus, problemin koşulundan, istenen sayıların eşit olmadığı sonucunu çıkarır, çünkü eğer eşit olsaydı, çarpımı 96 değil, 100 olurdu. toplamı, yani. 10+x, diğeri daha küçüktür, yani. 10'lar. Aralarındaki fark 2 kere .
Dolayısıyla denklem:
(10 + x)(10 - x) = 96
100 - x 2 = 96
x 2 - 4 = 0 (1)
Buradan x = 2. İstenilen numaralardan biri 12 , başka 8 . Çözüm x = -2 Diophantus diye bir şey yoktur, çünkü Yunan matematiği yalnızca pozitif sayıları biliyordu.
Bu problemi istenilen sayılardan birini bilinmeyen olarak seçerek çözersek denklemin çözümüne ulaşmış oluruz.
y(20 - y) = 96,
y 2 - 20y + 96 = 0. (2)
Diophantus'un bilinmeyen olarak istenen sayıların yarı farkını seçerek çözümü basitleştirdiği açıktır; sorunu, tamamlanmamış bir ikinci dereceden denklemi (1) çözmeye indirgemeyi başarır.
1.3 Hindistan'da ikinci dereceden denklemler
İkinci dereceden denklemler için problemler, Hintli matematikçi ve astronom Aryabhatta tarafından 499'da derlenen astronomik yol "Aryabhattam" da zaten bulundu. Başka bir Hintli bilim adamı, Brahmagupta (7. yüzyıl), tek bir kanonik forma indirgenmiş ikinci dereceden denklemleri çözmek için genel kuralı özetledi:
2+ b x = c, a > 0. (1)
(1) numaralı denklemde, katsayılar, a, olumsuz da olabilir. Brahmagupta'nın kuralı esasen bizimkiyle örtüşür.
Eski Hindistan'da, zor sorunları çözmede halka açık yarışmalar yaygındı. Eski Hint kitaplarından birinde, bu tür yarışmalar hakkında şunlar söylenir: "Güneş, parlaklığıyla yıldızları gölgede bırakıyorsa, bilgili bir kişi de halka açık toplantılarda, cebirsel problemleri önererek ve çözerek diğerinin görkemini gölgede bırakacaktır." Görevler genellikle şiirsel biçimde giyinirdi.
İşte XII.Yüzyılın ünlü Hintli matematikçisinin sorunlarından biri. Bhaskara.
Görev 13.
"Ufak bir maymun sürüsü Ve asmalarda on iki...
Güç yemiş, eğlenmiş. Atlamaya başladılar, asılı kaldılar ...
Sekizinci bölüm bir meydanda Kaç maymun vardı,
Çayırda eğlenmek. Bana bu sürüde mi söylüyorsun?
Bhaskara'nın çözümü, ikinci dereceden denklemlerin köklerinin iki değerliliğini bildiğini gösterir (Şekil 3).
Sorun 13'e karşılık gelen denklem:
( x /8) 2 + 12 = x
Bhaskara kisvesi altında yazıyor:
x 2 - 64x = -768
ve tamamlamak için Sol Taraf bu denklemin karesine, her iki tarafa da ekler 32 2 , o zaman almak:
x 2 - 64x + 32 2 = -768 + 1024,
(x - 32) 2 = 256,
x - 32 = ± 16,
x 1 = 16, x 2 = 48.
1.4 El-Khorezmi'de ikinci dereceden denklemler
Al-Khorezmi'nin cebirsel incelemesi, doğrusal ve ikinci dereceden denklemlerin bir sınıflandırmasını verir. Yazar, bunları aşağıdaki gibi ifade ederek 6 tür denklemi listeler:
1) "Kareler köklere eşittir", yani. eksen 2 + c = b X.
2) "Kareler sayıya eşittir", yani. eksen 2 = s.
3) "Kökler sayıya eşittir", yani. ah = s.
4) "Kareler ve sayılar köklere eşittir", yani. eksen 2 + c = b X.
5) "Kareler ve kökler sayıya eşittir", yani. 2+ sevgili = s.
6) "Kökler ve sayılar karelere eşittir", yani. sevgili + c \u003d eksen 2.
Negatif sayıları kullanmaktan kaçınan el-Harezmi için, bu denklemlerin her birinin terimleri çıkarma değil toplamadır. Bu durumda, pozitif çözümü olmayan denklemler açıkça dikkate alınmaz. Yazar, el-cebr ve el-mukabele yöntemlerini kullanarak bu denklemleri çözme yöntemlerini özetlemektedir. Onun kararları elbette bizimkilerle tamamen örtüşmüyor. Tamamen retorik olduğu gerçeğinden bahsetmiyorum bile, örneğin, birinci tip tamamlanmamış ikinci dereceden bir denklemi çözerken not edilmelidir.
El-Khorezmi, 17. yüzyıldan önceki tüm matematikçiler gibi, muhtemelen belirli pratik problemlerde önemli olmadığı için sıfır çözümü hesaba katmaz. Tam ikinci dereceden denklemleri çözerken, el-Khorezmi, belirli sayısal örnekler kullanarak çözme kurallarını ve ardından geometrik ispatları belirler.
Görev 14.“Kare ve 21 sayısı 10 köke eşittir. Kökünü bulun" (x 2 + 21 = 10x denkleminin kökü varsayılarak).
Yazarın çözümü şuna benzer: kök sayısını ikiye böl, 5 elde et, 5'i kendisiyle çarp, sonuçtan 21 çıkar, 4 kalır 4'ün kökünü al, 2'yi 5'ten çıkar, sen 3 olsun, bu istenen kök olacaktır. Veya 2'ye 5 ekleyin, bu da 7 verecek, bu da bir kök.
Risale-i Harezmi, ikinci dereceden denklemlerin sınıflandırılmasının sistematik olarak belirtildiği ve çözüm formüllerinin verildiği, bize ulaşan ilk kitaptır.
1.5 Avrupa'da ikinci dereceden denklemler XIII - XVII yüzyıllar
Avrupa'daki el-Khorezmi modelinde ikinci dereceden denklemleri çözmek için formüller ilk olarak 1202'de İtalyan matematikçi Leonardo Fibonacci tarafından yazılan "Abaküs Kitabı"nda ortaya kondu. Hem İslam ülkelerinde hem de Antik Yunanistan'da matematiğin etkisini yansıtan bu hacimli eser, hem bütünlük hem de sunum netliği ile ayırt edilir. Yazar bağımsız olarak bazı yeni cebirsel problem çözme örnekleri geliştirdi ve Avrupa'da negatif sayıların kullanılmasına ilk yaklaşan kişi oldu. Kitabı cebirsel bilginin sadece İtalya'da değil, Almanya, Fransa ve diğer Avrupa ülkelerinde de yayılmasına katkıda bulundu. "Abaküs Kitabı" ndan birçok görev, 16. - 17. yüzyılların neredeyse tüm Avrupa ders kitaplarına geçti. ve kısmen XVIII.
Tek bir kanonik forma indirgenmiş ikinci dereceden denklemleri çözmek için genel kural:
x 2+ sevgili = ile,
katsayıların tüm olası işaret kombinasyonları için b , İle birlikte Avrupa'da sadece 1544'te M. Stiefel tarafından formüle edilmiştir.
Vieta, ikinci dereceden bir denklemi çözmek için formülün genel bir türevine sahiptir, ancak Vieta yalnızca pozitif kökleri tanıdı. İtalyan matematikçiler Tartaglia, Cardano, Bombelli, 16. yüzyılda ilk olanlar arasındaydı. Olumlu ve olumsuz köklere ek olarak dikkate alın. Sadece XVII yüzyılda. Girard, Descartes, Newton ve diğerlerinin çalışmaları sayesinde bilim adamları yolu ikinci dereceden denklemleri çözmek modern bir biçim alır.
1.6 Vieta teoremi hakkında
İkinci dereceden bir denklemin katsayıları ile kökleri arasındaki ilişkiyi ifade eden Vieta adını taşıyan teorem, ilk kez 1591'de onun tarafından şu şekilde formüle edildi: B + Dçarpılır A - A 2 , eşittir BD, sonra A eşittir AT ve eşit D ».
Vieta'yı anlamak için şunu unutmamak gerekir. ANCAK, herhangi bir sesli harf gibi, onun için bilinmeyen anlamına geliyordu (bizim X), Sesli harfler AT, D- bilinmeyen için katsayılar. Modern cebir dilinde, Vieta'nın yukarıdaki formülasyonu şu anlama gelir: eğer
(bir + b )x - x 2 = ab ,
x 2 - (bir + b )x + bir b = 0,
x 1 = bir, x 2 = b .
Semboller kullanılarak yazılan genel formüllerle denklemlerin kökleri ve katsayıları arasındaki ilişkiyi ifade eden Viet, denklem çözme yöntemlerinde tekdüzelik kurdu. Ancak, Vieta'nın sembolizmi hala modern görünüm. Negatif sayıları tanımıyordu ve bu nedenle denklemleri çözerken sadece tüm köklerin pozitif olduğu durumları düşündü.
2. İkinci dereceden denklemleri çözme yöntemleri
İkinci dereceden denklemler, görkemli bina cebir. ikinci dereceden denklemler bulmak geniş uygulama trigonometrik, üstel, logaritmik, irrasyonel ve aşkın denklemleri ve eşitsizlikleri çözerken. Hepimiz okuldan (8. sınıf) mezuniyete kadar ikinci dereceden denklemleri nasıl çözeceğimizi biliyoruz.
Ana Sayfa > RaporHeroes adını taşıyan MOU ortaokulu Sovyetler Birliği
Sotnikova A.T. ve Shepeleva N.G. s. Uritskoe
Konuyla ilgili rapor:
"Çıkış tarihi
ikinci dereceden denklemler"
Tarafından hazırlandı:İzotova Julia,
Ampleeva Elena,
Shepelev Nikolay,
Dyachenko Yuri.
Ah matematik. Yüzyıllar boyunca ihtişamla kaplısın,
Tüm dünyevi armatürlerin armatürü.
seni görkemli kraliçe
Gauss'un vaftiz olmasına şaşmamalı.
Katı, mantıklı, görkemli,
Uçarken ince, ok gibi,
sonsuz zaferin
Çağlar boyunca ölümsüzlük kazandı.
İnsan aklını övüyoruz
onun işleri sihirli eller,
Bu çağın umudu
Tüm dünya bilimlerinin kraliçesi.
Bugün size söylemek istiyoruz
Olay tarihi
Her öğrencinin bilmesi gerekenler
İkinci dereceden denklemlerin tarihi.
Öklid, III yüzyılda M.Ö. e. ikinci dereceden denklemleri çözmek için gerekli tüm materyalleri içeren ikinci kitabın tamamını geometrik cebire adadığı "İlkeleri" nde.Euclid (Eνκλειδηζ), antik Yunan matematikçi, matematik üzerine bize ulaşan ilk teorik incelemenin yazarı
Öklid hakkında bilgi son derece azdır. Güvenilir sayılabilecek tek şey, bilimsel aktivite 3. yüzyılda İskenderiye'de aktı. e. Öklid, İskenderiye okulunun ilk matematikçisidir. Onun asıl iş"Başlangıçlar" (Latinceleştirilmiş biçimde - "Elementler") bir planimetri, stereometri ve sayı teorisindeki bir takım konuların bir sunumunu içerir; içinde Yunan matematiğinin önceki gelişimini özetledi ve temeli oluşturdu. Daha fazla gelişme matematik. Balıkçıl - MS 1. yüzyılda Yunanistan'da ilk kez Yunan matematikçi ve mühendis. ikinci dereceden bir denklemi çözmenin tamamen cebirsel bir yolunu verir.
İskenderiye Heron; Heron, ben c. n. e., Yunan makinist ve matematikçi. Hayatının zamanı belirsizdir, sadece Arşimet'ten (MÖ 212'de ölen) alıntı yaptığı bilinmektedir, kendisi Pappus tarafından alıntılanmıştır (MS 300). Şu anda hakim görüş, 1. yüzyılda yaşadığı yönündedir. n. e. Geometri, mekanik, hidrostatik, optik okudu; prototip buhar motorunu ve hassas tesviye aletlerini icat etti. En popüler otomatlar otomatik tiyatrolar, çeşmeler ve diğerleriydi.G. statik ve kinetik yasalarına dayanarak teodoliti tanımladı ve kaldıraç, blok, pervane ve askeri araçların bir tanımını verdi. Optikte, matematikte ışık yansıması yasalarını formüle etti - en önemli olanı ölçme yöntemleri geometrik şekiller. G.'nin başlıca eserleri şunlardır: Etrika, Pneumatics, Autopoietics, Mechanics (Fransızca; eser tamamen Arapça olarak korunmuştur), Catoptics (ayna bilimi; sadece Latince çeviri) ve diğerleri G. seleflerinin başarılarını kullandı: Lampsak'tan Öklid, Arşimet, Strato. Tarzı, bazen çok özlü veya yapılandırılmamış olsa da, basit ve açıktır. G.'nin yazılarına ilgi III. Yüzyılda ortaya çıktı. n. e. Yunan ve ardından Bizans ve Arap öğrenciler onun eserlerini yorumlayıp tercüme ettiler.
Diophantus- MS 3. yüzyılda bir Yunan bilim adamı, geometriye başvurmadan, bazı ikinci dereceden denklemleri tamamen cebirsel bir şekilde çözdü ve denklemin kendisi ve çözümü sembolik biçimde yazılmıştır.
“Size Yunan matematikçi Diophantus'un ikinci dereceden denklemleri nasıl oluşturduğunu ve çözdüğünü anlatacağım. Burada, örneğin, görevlerinden biri:"Toplamlarının 20 ve çarpımlarının 96 olduğunu bilen iki sayı bulun."
1. Problemin durumundan, istenen sayıların eşit olmadığı sonucu çıkar, çünkü eşit olsaydı, ürünleri 96 değil, 100 olurdu.
2. Böylece. bunlardan biri toplamlarının yarısından fazlası olacak, yani. 10 + x, diğeri daha azdır, yani. 10 - x.
3. Aralarındaki fark 2x'tir.
4. Dolayısıyla denklem (10 + x) * (10 - x) = 96
100 - x 2 = 96 x 2 - 4 = 0
5. Cevap x = 2. İstenen sayılardan biri 12'dir,
diğer - 8. Diophantus için x = - 2 çözümü yoktur, çünkü Yunan matematiği yalnızca pozitif sayıları biliyordu.”
Diophantus, bilinmeyen için kullanılan çok karmaşık denklemlerin nasıl çözüleceğini biliyordu. harf atamaları, hesaplama için özel bir sembol tanıttı, kullanılan kelime kısaltmaları. Bhaskare - Akarya- MS XII.Yüzyılda Hintli matematikçi. açıldı genel yöntem ikinci dereceden denklemlerin çözümleri.
Hintli matematikçilerin problemlerinden birini, örneğin Bhaskara problemini analiz edelim:
“Bir maymun sürüsü eğleniyor: toplam sayının sekizde biri ormanda kare bir oyun oynuyor, kalan on iki höyüğün tepesinde çığlık atıyor. Söyle bana, orada kaç maymun var?"
Problem hakkında yorum yaparken (x/8) 2 + 12 = x denkleminin probleme karşılık geldiğini söylemek isterim. Bhaskara, x 2 - 64x \u003d - 768 olarak yazar. Her iki parçaya da kare 32 eklendiğinde denklem şu şekilde olur:
x 2 - 64 x + 32 2 = - 768 + 1024
(x - 32) 2 = 256
Karekökü çıkardıktan sonra şunu elde ederiz: x - 32 = 16.
"AT bu durum, diyor Bhaskara, - ilk bölümün negatif birimleri, ikinci bölümün birimleri onlardan daha az olacak şekildedir ve bu nedenle ikincisi hem pozitif hem de negatif olarak kabul edilebilir ve bilinmeyenin iki katı değerini elde ederiz: 48 ve 16.
Bhaskara'nın çözümünün, ikinci dereceden denklemlerin köklerinin iki değerliliğini bildiğini gösterdiği sonucuna varılmalıdır.
Eski Hint Bhaskara problemini çözmesi önerildi:
“Maymunların beşte birinin karesi, üçe indirilmiş, mağaraya saklanmış, bir maymun ağaca tırmanmış, görünüyordu. Kaç maymun vardı? Bu sorunun, ikinci dereceden bir denkleme indirgenerek temel olarak çözüldüğüne dikkat edilmelidir. Al - Harezmi
- 825'te "Restorasyon ve Muhalefet Kitabı" kitabını yazan bir Arap bilgini. Dünyanın ilk cebir ders kitabıydı. Ayrıca altı tür ikinci dereceden denklem verdi ve sözlü olarak formüle ettiği altı denklemin her biri için onu çözmek için özel bir kural verdi. Harezmi risalede 6 tür denklemi sıralayarak bunları şu şekilde ifade eder:
Al - Harezmi
- 825'te "Restorasyon ve Muhalefet Kitabı" kitabını yazan bir Arap bilgini. Dünyanın ilk cebir ders kitabıydı. Ayrıca altı tür ikinci dereceden denklem verdi ve sözlü olarak formüle ettiği altı denklemin her biri için onu çözmek için özel bir kural verdi. Harezmi risalede 6 tür denklemi sıralayarak bunları şu şekilde ifade eder: 1. "Kareler köklere eşittir", yani. balta 2 = içinde.
2. "Kareler sayıya eşittir", yani. eksen 2 = s.
3. "Kökler sayıya eşittir", yani. ah = s.
4. "Kareler ve sayılar köklere eşittir", yani. balta 2 + c \u003d inç.
5. "Kareler ve kökler sayıya eşittir", yani. eksen 2 + in = s.
6. "Kökler ve sayılar karelere eşittir", yani. + c \u003d ah 2'de.İkinci dereceden bir denklemi çözmeye indirgenen el-Harezmi problemini inceleyelim. "Bir kare ve bir sayı köklere eşittir." Örneğin, bir kare ve 21 sayısı aynı karenin 10 köküne eşittir, yani. Soru şu ki, kendisine 21 eklendikten sonra aynı karenin 10 köküne eşit olan bir kare ne oluşur?
Ve  Harezmi'nin 4. formülünü kullanarak öğrenciler şunu yazmalıdır: x 2 + 21 = 10x
Harezmi'nin 4. formülünü kullanarak öğrenciler şunu yazmalıdır: x 2 + 21 = 10x
François Viet - Fransız matematikçi, verilen ikinci dereceden denklemin köklerinin toplamı ve çarpımı üzerinde teoremi formüle etti ve kanıtladı.
Benim sunduğum sanat yeni ya da en azından barbarların etkisiyle o kadar yozlaştı ki, ona tamamen yeni bir görünüm kazandırmayı uygun gördüm.
François Viet
Yine de François (1540-13.12. 1603) Poitou ilindeki Fontenay-le-Comte kasabasında, ünlü La Rochelle kalesinin yakınında doğdu. Hukuk diploması aldıktan sonra, on dokuz yaşından itibaren başarılı bir şekilde avukatlık yaptı. Memleket. Bir avukat olarak Viet, halk arasında prestij ve saygı gördü. Geniş eğitimli bir insandı. Astronomi ve matematik ve her şeyi biliyordu boş zaman bu bilimlere verdi.
Ana tutku Vieta matematikti. Cardano, Bombelli, Stevin ve diğerlerinin öncülleri olan klasik Arşimet ve Diophantus'un eserlerini derinlemesine inceledi. Vieta onlara sadece hayran olmakla kalmadı, aynı zamanda sözlü sembolizm nedeniyle anlaşılması güç olan büyük bir kusur gördü: Neredeyse tüm eylemler ve işaretler kelimelerle kaydedildi, şimdi kullandığımız bu kullanışlı, neredeyse otomatik kurallardan hiçbir ipucu yoktu. . Cebirsel karşılaştırmalar veya diğer herhangi bir cebirsel ifadeyi yazmak ve bu nedenle genel bir biçimde başlamak imkansızdı. Sayısal katsayılı her denklem türü özel bir kurala göre çözülmüştür. Bu nedenle, var olduğunu kanıtlamak gerekliydi. genel eylemler bu sayıların kendilerine bağlı olmayan tüm sayılar üzerinde. Viet ve takipçileri, söz konusu sayının nesne sayısı mı yoksa parçanın uzunluğu mu olduğunun önemli olmadığını tespit ettiler. Ana şey, bu sayılarla cebirsel işlemler yapmanın ve sonuç olarak yine aynı türden sayıların elde edilmesinin mümkün olmasıdır. Bu nedenle, bazı soyut işaretlerle gösterilebilirler. Viet tam da bunu yaptı. Sadece gerçek hesabını tanıtmakla kalmadı, aynı zamanda temel olarak yeni bir keşif yaptı ve kendisine sayıları değil, onlar üzerindeki eylemleri incelemeyi hedefledi. Bu kayıt yöntemi, Vieta'nın çalışırken önemli keşifler yapmasına izin verdi. ortak özellikler cebirsel denklemler. Harf sembollerinin kurucusu olan Vieta'nın cebirin "babası" olarak adlandırılması tesadüf değildir.

http :// som. fio. tr/ kaynaklar/ Karpuhina/2003/12/ Tamamlanmış%20 iş/ Konser/ dizin1. htm
http :// sayfalar. marsu. tr/ iac/ okul/ s4/ sayfa74. html