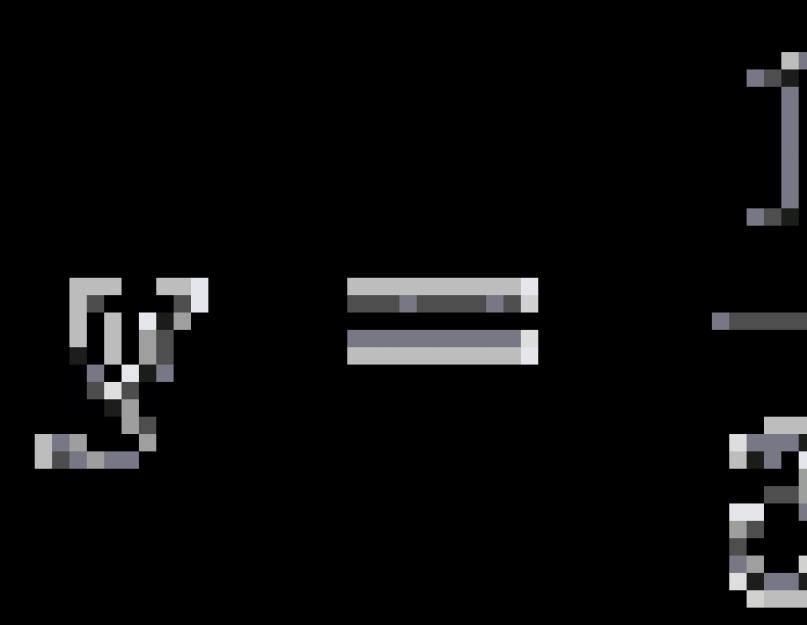Örnek 1. Bir fonksiyon verildiğinde F(X) = 3X 2 + 4X– 5. Fonksiyonun grafiğine teğetin denklemini yazalım. F(X) apsisli grafik noktasında X 0 = 1.

Çözüm. Bir fonksiyonun türevi F(X) herhangi bir x için mevcuttur R . Onu bulalım:

= (3X 2 + 4X– 5)' = 6 X + 4.

Daha sonra F(X 0) = F(1) = 2; (X 0) = = 10. Teğet denklem şu şekildedir:

sen = (X 0) (X – X 0) + F(X 0),

sen = 10(X – 1) + 2,

sen = 10X – 8.

Cevap. sen = 10X – 8.

Örnek 2. Bir fonksiyon verildiğinde F(X) = X 3 – 3X 2 + 2X+ 5. Fonksiyonun grafiğine teğet denklemini yazalım F(X), çizgiye paralel sen = 2X – 11.

Çözüm. Bir fonksiyonun türevi F(X) herhangi bir x için mevcuttur R . Onu bulalım:

= (X 3 – 3X 2 + 2X+ 5)' = 3 X 2 – 6X + 2.

Fonksiyonun grafiğine teğet olduğundan F(X) apsis noktasında X 0 doğruya paraleldir sen = 2X– 11 ise eğimi 2’ye eşittir, yani ( X 0) = 2. Bu apsisi 3 şartından bulalım. X– 6X 0 + 2 = 2. Bu eşitlik yalnızca şu durumlarda geçerlidir: X 0 = 0 ve X 0 = 2. Her iki durumda da F(X 0) = 5, sonra düz sen = 2X + B fonksiyonun grafiğine ya (0; 5) noktasında ya da (2; 5) noktasında dokunur.

İlk durumda, sayısal eşitlik 5 = 2×0 + doğrudur B, Neresi B= 5 ve ikinci durumda sayısal eşitlik 5 = 2×2 + doğrudur B, Neresi B = 1.

Yani iki teğet var sen = 2X+ 5 ve sen = 2X Fonksiyonun grafiğine +1 F(X), çizgiye paralel sen = 2X – 11.

Cevap. sen = 2X + 5, sen = 2X + 1.

Örnek 3. Bir fonksiyon verildiğinde F(X) = X 2 – 6X+ 7. Fonksiyonun grafiğine teğet denklemini yazalım F(X), noktadan geçerken A (2; –5).

Çözüm.Çünkü F(2) –5, ardından noktayı işaretleyin A fonksiyonun grafiğine ait değil F(X). İzin vermek X 0 - teğet noktasının apsisi.

Bir fonksiyonun türevi F(X) herhangi bir x için mevcuttur R . Onu bulalım:

= (X 2 – 6X+ 1)' = 2 X – 6.

Daha sonra F(X 0) = X– 6X 0 + 7; (X 0) = 2X 0 – 6. Teğet denklem şu şekildedir:

sen = (2X 0 – 6)(X – X 0) + X– 6X+ 7,

sen = (2X 0 – 6)X– X+ 7.

noktadan beri A teğete aitse sayısal eşitlik doğrudur

–5 = (2X 0 – 6)×2– X+ 7,

Neresi X 0 = 0 veya X 0 = 4. Bu şu anlama gelir: nokta boyunca A fonksiyonun grafiğine iki teğet çizebilirsiniz F(X).

Eğer X 0 = 0 ise teğet denklem şu şekildedir: sen = –6X+ 7. Eğer X 0 = 4 ise teğet denklem şu şekildedir: sen = 2X – 9.

Cevap. sen = –6X + 7, sen = 2X – 9.

Örnek 4. Verilen işlevler F(X) = X 2 – 2X+2 ve G(X) = –X 2 – 3. Bu fonksiyonların grafiklerine ortak teğet denklemini yazalım.

Çözüm.İzin vermek X 1 - fonksiyonun grafiği ile istenen çizginin teğet noktasının apsisi F(X), A X 2 - fonksiyonun grafiği ile aynı çizginin teğet noktasının apsisi G(X).

Bir fonksiyonun türevi F(X) herhangi bir x için mevcuttur R . Onu bulalım:

= (X 2 – 2X+ 2)' = 2 X – 2.

Daha sonra F(X 1) = X– 2X 1 + 2; (X 1) = 2X 1 – 2. Teğet denklem şu şekildedir:

sen = (2X 1 – 2)(X – X 1) + X– 2X 1 + 2,

sen = (2X 1 – 2)X – X+ 2. (1)

Fonksiyonun türevini bulalım G(X):

= (–X 2 – 3)' = –2 X.

Aşağıdaki şekli göz önünde bulundurun:

a noktasında türevi olabilen belirli bir y = f(x) fonksiyonunu gösterir. Koordinatları (a; f(a)) olan M noktası işaretlenmiştir. Grafiğin rastgele bir P(a + ∆x; f(a + ∆x)) noktasından geçen bir sekant MR çizilir.

Şimdi P noktası grafik boyunca M noktasına kaydırılırsa, o zaman MR düz çizgisi M noktası etrafında dönecektir. Bu durumda ∆x sıfıra yönelecektir. Buradan bir fonksiyonun grafiğine teğetin tanımını formüle edebiliriz.

Bir fonksiyonun grafiğine teğet

Bir fonksiyonun grafiğine teğet, argümanın artışı sıfıra yaklaştıkça sekantın sınırlayıcı konumudur. f fonksiyonunun türevinin x0 noktasında bulunması, grafiğin bu noktasında teğet ona.

Bu durumda tanjantın açısal katsayısı bu fonksiyonun f’(x0) noktasındaki türevine eşit olacaktır. Türevin geometrik anlamı budur. x0 noktasında diferansiyellenebilir bir f fonksiyonunun grafiğine teğet, (x0;f(x0)) noktasından geçen ve f'(x0) açısal katsayısına sahip belirli bir düz çizgidir.

Teğet denklem

A(x0; f(x0)) noktasındaki bir f fonksiyonunun grafiğine teğet denklemini elde etmeye çalışalım. Eğimi k olan bir doğrunun denklemi aşağıdaki biçimdedir:

Eğim katsayımız türevimize eşit olduğundan f'(x0) ise denklem şu formu alacaktır: y = f'(x0)*x + b.

Şimdi b'nin değerini hesaplayalım. Bunu yapmak için fonksiyonun A noktasından geçtiği gerçeğini kullanırız.

f(x0) = f'(x0)*x0 + b, buradan b'yi ifade ederiz ve b = f(x0) - f'(x0)*x0 elde ederiz.

Ortaya çıkan değeri teğet denklemde değiştiririz:

y = f'(x0)*x + b = f'(x0)*x + f(x0) - f'(x0)*x0 = f(x0) + f'(x0)*(x - x0).

y = f(x0) + f’(x0)*(x - x0).

Şu örneği düşünün: f(x) = x 3 - 2*x 2 + 1 fonksiyonunun grafiğine x = 2 noktasındaki teğet denklemini bulun.

2. f(x0) = f(2) = 2 2 - 2*2 2 + 1 = 1.

3. f'(x) = 3*x 2 - 4*x.

4. f'(x0) = f'(2) = 3*2 2 - 4*2 = 4.

5. Elde edilen değerleri teğet formülünde yerine koyarsak şunu elde ederiz: y = 1 + 4*(x - 2). Parantezleri açıp benzer terimleri getirdiğimizde şunu elde ederiz: y = 4*x - 7.

Cevap: y = 4*x - 7.

Teğet denklemini oluşturmak için genel şema y = f(x) fonksiyonunun grafiğine:

1. x0'ı belirleyin.

2. f(x0)'ı hesaplayın.

3. f’(x)’i hesaplayın

Açık modern sahne Eğitimin geliştirilmesinde ana görevlerden biri yaratıcı düşünen bir kişiliğin oluşmasıdır. Öğrencilerde yaratıcılık yeteneği ancak sistematik olarak temel konulara dahil olmaları durumunda geliştirilebilir. araştırma faaliyetleri. Öğrencilerin yaratıcı güçlerini, yeteneklerini ve yeteneklerini kullanabilmelerinin temeli tam teşekküllü bilgi ve becerilerden oluşur. Bu bağlamda, okul matematik dersinin her konusu için bir temel bilgi ve beceri sistemi oluşturma sorunu hiç de azımsanmayacak bir öneme sahiptir. Aynı zamanda tam teşekküllü becerilere sahip olunmalıdır. didaktik amaç bireysel görevler değil, dikkatlice düşünülmüş bir sistem. En geniş anlamda bir sistem, bütünlüğe ve istikrarlı bir yapıya sahip, birbirine bağlı, etkileşimli öğeler kümesi olarak anlaşılmaktadır.

Öğrencilere bir fonksiyonun grafiğine teğet için denklem yazmayı öğreten bir teknik düşünelim. Esasen, teğet denklemi bulmayla ilgili tüm problemler, belirli bir gereksinimi karşılayan bir dizi (paket, aile) çizgi arasından seçim yapma ihtiyacına iner - bunlar belirli bir fonksiyonun grafiğine teğettir. Bu durumda seçimin gerçekleştirileceği satır kümesi iki şekilde belirlenebilir:

a) xOy düzleminde yer alan bir nokta (merkezi çizgi kalemi);
b) açısal katsayı (düz çizgilerden oluşan paralel ışın).

Bu bağlamda, sistemin elemanlarını izole etmek için “Bir fonksiyonun grafiğine teğet” konusunu incelerken iki tür problem belirledik:

1) içinden geçtiği noktanın verdiği teğet üzerindeki problemler;
2) eğiminin verdiği teğet üzerindeki problemler.

Teğet problemlerin çözümüne yönelik eğitim, A.G. tarafından önerilen algoritma kullanılarak gerçekleştirildi. Mordkoviç. Zaten bilinenlerden temel farkı, teğet noktasının apsisinin a harfiyle (x0 yerine) gösterilmesi ve dolayısıyla teğet denkleminin şu şekli almasıdır:

y = f(a) + f "(a)(x – a)

(y = f(x 0) + f "(x 0)(x – x 0) ile karşılaştırın). Bu metodik teknik Kanaatimizce öğrencilerin genel teğet denkleminde mevcut noktanın koordinatlarının nerede yazıldığını, teğet noktalarının nerede olduğunu hızlı ve kolay bir şekilde anlamalarını sağlar.

y = f(x) fonksiyonunun grafiğine teğet denklemi oluşturma algoritması

1. Teğet noktasının apsisini a harfiyle belirtin.
2. f(a)'yı bulun.
3. f "(x) ve f "(a)'yı bulun.
4. Bulunan a, f(a), f "(a) sayılarını yerine koyun genel denklem teğet y = f(a) = f "(a)(x – a).

Bu algoritma, öğrencilerin bağımsız olarak işlemleri tanımlamaları ve uygulama sıraları temel alınarak derlenebilir.

Uygulama, bir algoritma kullanarak anahtar problemlerin her birinin sıralı çözümünün, bir fonksiyonun grafiğine teğet denklemini aşamalar halinde yazma becerilerini geliştirmenize izin verdiğini ve algoritmanın adımlarının eylemler için referans noktaları görevi gördüğünü göstermiştir. . Bu yaklaşım teoriyle tutarlıdır. kademeli oluşum P.Ya. tarafından geliştirilen zihinsel eylemler. Galperin ve N.F. Talyzina.

İlk görev türünde iki temel görev belirlendi:

• teğet eğri üzerinde bulunan bir noktadan geçer (problem 1);
• teğet eğrinin üzerinde olmayan bir noktadan geçiyor (problem 2).

Görev 1. Fonksiyonun grafiğine teğet için bir denklem yazın M(3; – 2) noktasında.

Çözüm. M(3; – 2) noktası bir teğet noktadır, çünkü

1. a = 3 – teğet noktasının apsisi.
2. f(3) = – 2.
3. f "(x) = x 2 – 4, f "(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – teğet denklemi.

Problem 2. M(– 3; 6) noktasından geçen y = – x 2 – 4x + 2 fonksiyonunun grafiğine tüm teğetlerin denklemlerini yazın.

Çözüm. M(– 3; 6) noktası f(– 3) 6 olduğundan teğet nokta değildir (Şekil 2).

2. f(a) = – a 2 – 4a + 2.
3. f "(x) = – 2x – 4, f "(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – teğet denklemi.

Teğet M(- 3; 6) noktasından geçer, dolayısıyla koordinatları teğet denklemini sağlar.

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a),
a 2 + 6a + 8 = 0 ^ a 1 = – 4, a 2 = – 2.

a = – 4 ise teğet denklemi y = 4x + 18 olur.

a = – 2 ise teğet denklem y = 6 biçiminde olur.

İkinci tipte temel görevler aşağıdakiler olacaktır:

• teğet bir doğruya paraleldir (sorun 3);
• teğet verilen doğruya belirli bir açıyla geçiyor (problem 4).

Problem 3. y = x 3 – 3x 2 + 3 fonksiyonunun grafiğine y = 9x + 1 doğrusuna paralel olan tüm teğetlerin denklemlerini yazın.

1. a – teğet noktasının apsisi.
2. f(a) = a 3 – 3a 2 + 3.
3. f "(x) = 3x 2 – 6x, f "(a) = 3a 2 – 6a.

Ancak diğer taraftan f"(a) = 9 (paralellik koşulu). Bu da 3a 2 – 6a = 9 denklemini çözmemiz gerektiği anlamına geliyor. Kökleri a = – 1, a = 3'tür (Şekil 3). ).

4.1) a = – 1;
2) f(– 1) = – 1;
3) f "(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 – teğet denklem;

1) bir = 3;
2) f(3) = 3;
3) f "(3) = 9;
4) y = 3 + 9(x – 3);

y = 9x – 24 – teğet denklemi.

Problem 4. y = 0,5x 2 – 3x + 1 fonksiyonunun grafiğine, y = 0 düz çizgisine 45° açıyla geçen teğetin denklemini yazın (Şekil 4).

Çözüm. f "(a) = tan 45° koşulundan a: a – 3 = 1 ^ a = 4'ü buluruz.

1. a = 4 – teğet noktasının apsisi.
2. f(4) = 8 – 12 + 1 = – 3.
3.f"(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).

y = x – 7 – teğet denklemi.

Başka herhangi bir sorunun çözümünün bir veya daha fazla temel sorunun çözümüne bağlı olduğunu göstermek kolaydır. Örnek olarak aşağıdaki iki sorunu düşünün.

1. Teğetler dik açılarda kesişiyorsa ve bunlardan biri parabole apsis 3 noktasında değiyorsa, y = 2x 2 – 5x – 2 parabolüne teğetlerin denklemlerini yazın (Şekil 5).

Çözüm. Teğet noktasının apsisi verildiğinden çözümün ilk kısmı anahtar problem 1'e indirgenir.

1. a = 3 – dik açının kenarlarından birinin teğet noktasının apsisi.
2. f(3) = 1.
3. f "(x) = 4x – 5, f "(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – birinci teğetin denklemi.

İlk teğetin eğim açısı a olsun. Teğetler birbirine dik olduğundan ikinci teğetin eğim açısı olur. İlk teğetin y = 7x – 20 denkleminden tg a = 7 elde ederiz.

Bu, ikinci teğetin eğiminin eşit olduğu anlamına gelir.

Daha fazla çözüm 3. temel göreve geliyoruz.

B(c; f(c)) ikinci doğrunun teğet noktası olsun, o zaman

1. – ikinci teğet noktasının apsisi.
2.
3.
4.
– ikinci teğetin denklemi.

Not. Öğrenciler dik doğruların katsayılarının oranını k 1 k 2 = – 1 olarak bilirlerse tanjantın açısal katsayısı daha kolay bulunabilir.

2. Fonksiyonların grafiklerine tüm ortak teğetlerin denklemlerini yazın

Çözüm. Sorun, ortak teğetlerin teğet noktalarının apsisini bulmak, yani temel problem 1'i çözmekle ilgilidir. genel görünüm, bir denklem sistemi ve sonraki çözümü hazırlamak (Şekil 6).

1. y = x 2 + x + 1 fonksiyonunun grafiğinde yer alan teğet noktasının apsisi a olsun.
2. f(a) = a 2 + a + 1.
3.f "(a) = 2a + 1.
4. y = a 2 + a + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – a 2 .

1. Fonksiyonun grafiğinde yer alan teğet noktasının apsisi c olsun
2.
3.f "(c) = c.
4.

Teğetler genel olduğundan,

Yani y = x + 1 ve y = – 3x – 3 ortak teğetlerdir.

Göz önünde bulundurulan görevlerin temel amacı, öğrencileri, belirli araştırma becerilerini (analiz etme, karşılaştırma, genelleme, hipotez öne sürme vb.) gerektiren daha karmaşık problemleri çözerken anahtar problemin türünü bağımsız olarak tanımaya hazırlamaktır. Bu tür görevler, herhangi bir görevi içerir. anahtar görev bileşen olarak dahil edilmiştir. Örnek olarak, teğet ailesinden bir fonksiyon bulma problemini (Problem 1'in tersi) ele alalım.

3. y = x ve y = – 2x doğruları hangi b ve c için y = x 2 + bx + c fonksiyonunun grafiğine teğettir?

y = x düz çizgisinin y = x 2 + bx + c parabolüne göre teğet noktasının apsisi t olsun; p, y = x 2 + bx + c parabolüne sahip y = – 2x düz çizgisinin teğet noktasının apsisidir. O zaman y = x teğet denklemi y = (2t + b)x + c – t 2 formunu, y = – 2x teğet denklemi ise y = (2p + b)x + c – p 2 formunu alacaktır. .

Bir denklem sistemi oluşturup çözelim

Cevap:

Bu matematik programı, kullanıcı tarafından belirlenen bir \(a\) noktasında \(f(x)\) fonksiyonunun grafiğine teğet denklemini bulur.

Program sadece teğet denklemini göstermekle kalmıyor, aynı zamanda problemin çözüm sürecini de gösteriyor.

Bu çevrimiçi hesap makinesi lise öğrencileri için yararlı olabilir orta okullar hazırlık aşamasında testler ve sınavlar, Birleşik Devlet Sınavından önce bilgiyi test ederken, ebeveynlerin matematik ve cebirdeki birçok problemin çözümünü kontrol etmeleri için. Ya da belki bir öğretmen tutmak ya da yeni ders kitapları satın almak sizin için çok mu pahalı? Yoksa mümkün olduğu kadar çabuk halletmek mi istiyorsunuz? Ev ödevi

matematikte mi yoksa cebirde mi? Bu durumda detaylı çözümlere sahip programlarımızı da kullanabilirsiniz.

Bu sayede hem kendi eğitiminizi hem de küçük kardeşlerinizin eğitimini yürütebilir, sorun çözme alanındaki eğitim düzeyi de artar.

Bir fonksiyonun türevini bulmanız gerekiyorsa, bunun için türevi bulma görevimiz vardır.

İşlevlere girme kurallarına aşina değilseniz, bunları öğrenmenizi öneririz.

Fonksiyon ifadesini \(f(x)\) ve \(a\) sayısını girin
f(x)=

a=

Teğet denklemi bulun
Bu sorunu çözmek için gerekli olan bazı scriptlerin yüklenmediği ve programın çalışmayabileceği tespit edildi.
AdBlock'u etkinleştirmiş olabilirsiniz.

Bu durumda devre dışı bırakın ve sayfayı yenileyin.
Tarayıcınızda JavaScript devre dışı bırakıldı.
Çözümün görünmesi için JavaScript'i etkinleştirmeniz gerekir.

Tarayıcınızda JavaScript'i nasıl etkinleştireceğinize ilişkin talimatları burada bulabilirsiniz.
Çünkü Sorunu çözmek isteyen çok kişi var, talebiniz sıraya alındı.
Birkaç saniye içinde çözüm aşağıda görünecektir. Lütfen bekleyin

saniye... eğer sençözümde bir hata fark ettim
, ardından Geri Bildirim Formu'na bu konuda yazabilirsiniz. unutma hangi görevi belirtin ne olduğuna sen karar ver.

alanlara girin

Oyunlarımız, bulmacalarımız, emülatörlerimiz:

Küçük bir teori.

Doğrudan eğim Programın olduğunu unutmayalım doğrusal fonksiyon \(y=kx+b\) düz bir çizgidir. \(k=tg \alpha \) sayısına denir düz bir çizginin eğimi

ve \(\alpha \) açısı bu çizgi ile Ox ekseni arasındaki açıdır

M(a; f(a)) noktası y = f(x) fonksiyonunun grafiğine aitse ve bu noktada fonksiyonun grafiğine x eksenine dik olmayan bir teğet çizilebiliyorsa, daha sonra türevin geometrik anlamından, teğetin açısal katsayısının f "(a)'ya eşit olduğu sonucu çıkar. Daha sonra, herhangi bir fonksiyonun grafiğine teğet için bir denklem oluşturmak için bir algoritma geliştireceğiz.

Bu fonksiyonun grafiğinde y = f(x) fonksiyonu ve M(a; f(a)) noktası verilsin; f"(a)'nın var olduğu bilinsin. Grafiğe teğet için bir denklem oluşturalım Verilen fonksiyon belirli bir noktada. Bu denklem, ordinat eksenine paralel olmayan herhangi bir düz çizginin denklemi gibi y = kx + b formuna sahiptir, dolayısıyla görev k ve b katsayılarının değerlerini bulmaktır.

k açısal katsayısı ile ilgili her şey açıktır: k = f"(a) olduğu bilinmektedir. b'nin değerini hesaplamak için, istenen düz çizginin M(a; f(a)) noktasından geçtiği gerçeğini kullanırız. Bu, M noktasının koordinatlarını bir düz çizgi denkleminde yerine koyarsak doğru eşitliği elde ettiğimiz anlamına gelir: \(f(a)=ka+b\), yani \(b = f(a) - ka\).

K ve b katsayılarının bulunan değerlerini düz çizgi denkleminde değiştirmek kalır:

$$ y=kx+b $$ $$ y=kx+ f(a) - ka $$ $$ y=f(a)+ k(x-a) $$ $$ y=f(a)+ f"(a )(x-a)$$

Aldık bir fonksiyonun grafiğine teğet denklemi\(y = f(x) \) \(x=a \) noktasında.

\(y=f(x)\) fonksiyonunun grafiğine teğet denklemini bulma algoritması
1. Teğet noktasının apsisini \(a\) harfiyle belirtin
2. \(f(a)\)'yı hesaplayın
3. \(f"(x)\)'yi bulun ve \(f"(a)\)'yı hesaplayın
4. Bulunan \(a, f(a), f"(a) \) sayılarını \(y=f(a)+ f"(a)(x-a) \) formülünde değiştirin

Kitaplar (ders kitapları) Birleşik Devlet Sınavı özetleri ve Çevrimiçi Birleşik Devlet Sınavı testleri Oyunlar, bulmacalar İşlev grafikleri çizme Rus dilinin yazım sözlüğü Gençlik argo sözlüğü Rus okulları kataloğu Rusya orta öğretim kurumları kataloğu Rus üniversiteleri kataloğu Liste problemlerin listesi GCD ve LCM'yi bulma Bir polinomun basitleştirilmesi (polinomların çarpılması)

Makale, tanımların ayrıntılı bir açıklamasını, türevin geometrik anlamını grafik gösterimlerle sunmaktadır. Teğet doğrunun denklemi örneklerle ele alınacak, 2. mertebeden eğrilere teğet denklemler bulunacak.

Yandex.RTB R-A-339285-1 Tanım 1

y = k x + b düz çizgisinin eğim açısına α açısı denir ve bu açı, x ekseninin pozitif yönünden pozitif yönde y = k x + b düz çizgisine kadar ölçülür.

Şekilde x yönü yeşil ok ve yeşil yay ile, eğim açısı ise kırmızı yay ile gösterilmiştir. Mavi çizgi düz çizgiyi ifade eder.

Tanım 2

y = k x + b düz çizgisinin eğimine sayısal katsayı k denir.

Açısal katsayı düz çizginin tanjantına eşittir, diğer bir deyişle k = t g α.

• Düz bir çizginin eğim açısı yalnızca x'e göre paralelse ve eğim sıfıra eşitse 0'a eşittir çünkü sıfırın tanjantı 0'a eşittir. Bu, denklemin formunun y = b olacağı anlamına gelir.
• Eğer y = k x + b düz çizgisinin eğim açısı dar ise, o zaman 0 koşulu sağlanır< α < π 2 или 0 ° < α < 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α >0 ve grafikte bir artış var.
• Eğer α = π 2 ise doğrunun konumu x'e diktir. Eşitlik x = c ile belirtilir ve c değeri bir gerçek sayıdır.
• Düz çizginin eğim açısı y = k x + b genişse, o zaman π 2 koşullarına karşılık gelir< α < π или 90 ° < α < 180 ° , значение углового коэффициента k принимает negatif değer ve grafik azalıyor.

Tanım 3

Kesen, f(x) fonksiyonunun 2 noktasından geçen bir çizgidir. Başka bir deyişle sekant, belirli bir fonksiyonun grafiğindeki herhangi iki noktadan çizilen düz bir çizgidir.

Şekil A B'nin bir sekant olduğunu ve f(x)'in siyah bir eğri olduğunu, α'nın ise sekantın eğim açısını gösteren kırmızı bir yay olduğunu göstermektedir.

Düz bir çizginin açısal katsayısı eğim açısının tanjantına eşit olduğunda, bir A B C dik üçgeninin tanjantının karşı tarafın bitişik olana oranıyla bulunabileceği açıktır.

Tanım 4

Formun bir sekantını bulmak için bir formül elde ederiz:

k = t g α = B C A C = f (x B) - f x A x B - x A, burada A ve B noktalarının apsisleri x A, x B ve f (x A), f (x) değerleridir B) bu noktalardaki değer fonksiyonlarıdır.

Açıkçası, sekantın açısal katsayısı k = f (x B) - f (x A) x B - x A veya k = f (x A) - f (x B) x A - x B eşitliği kullanılarak belirlenir. ve denklem şu şekilde yazılmalıdır: y = f (x B) - f (x A) x B - x A x - x A + f (x A) veya
y = f (x A) - f (x B) x A - x B x - x B + f (x B) .

Sekant, grafiği görsel olarak 3 parçaya böler: A noktasının solunda, A'dan B'ye ve B'nin sağında. Aşağıdaki şekil, çakıştığı düşünülen üç sekantın olduğunu, yani bunların bir kullanılarak ayarlandığını göstermektedir. benzer denklem.

Tanım gereği, bir düz çizgi ve onun keseninin olduğu açıktır. bu durumda kibrit.

Bir sekant belirli bir fonksiyonun grafiğini birden çok kez kesebilir. Bir sekant için y = 0 formunda bir denklem varsa, sinüzoidle kesişme noktalarının sayısı sonsuzdur.

Tanım 5

f(x) fonksiyonunun grafiğine x 0 noktasında teğet; f (x 0), belirli bir x 0 noktasından geçen düz bir çizgidir; f (x 0), x 0'a yakın birçok x değerine sahip bir segmentin varlığıyla.

Örnek 1

Aşağıdaki örneğe daha yakından bakalım. O zaman y = x + 1 fonksiyonuyla tanımlanan doğrunun (1; 2) koordinatlı noktada y = 2 x'e teğet olduğu kabul edilir. Netlik sağlamak için (1; 2)'ye yakın değerlere sahip grafikleri dikkate almak gerekir. Y = 2 x fonksiyonu siyahla gösterilmiştir, mavi çizgi teğet çizgidir ve kırmızı nokta kesişme noktasıdır.

Açıkçası, y = 2 x, y = x + 1 doğrusuyla birleşiyor.

Teğeti belirlemek için, B noktası A noktasına sonsuz yaklaşırken A B teğetinin davranışını düşünmeliyiz. Açıklık sağlamak için bir çizim sunuyoruz.

Mavi çizgiyle gösterilen sekant A B, teğetin kendisinin konumuna yönelir ve sekant α'nın eğim açısı, teğetin kendisinin αx eğim açısına yönelmeye başlayacaktır.

Tanım 6

y = f(x) fonksiyonunun grafiğinin A noktasındaki teğeti, B'nin A'ya yönelmesiyle, yani B → A'yla kesişen A B'nin sınırlayıcı konumu olarak kabul edilir.

Şimdi bir fonksiyonun bir noktadaki türevinin geometrik anlamını ele almaya geçelim.

F (x) fonksiyonu için A B sekantını ele almaya devam edelim; burada x 0, f (x 0) ve x 0 + ∆ x, f (x 0 + ∆ x) ve ∆ x koordinatlarına sahip A ve B, argümanın artışı olarak gösterilir. Artık fonksiyon ∆ y = ∆ f (x) = f (x 0 + ∆ x) - f (∆ x) formunu alacaktır. Açıklık sağlamak için bir çizim örneği verelim.

Sonucu değerlendirelim dik üçgen A B C. Çözmek için teğet tanımını kullanırız, yani ∆ y ∆ x = t g α ilişkisini elde ederiz. Teğetin tanımından şu sonuç çıkar: lim ∆ x → 0 ∆ y ∆ x = t g α x. Bir noktadaki türev kuralına göre, x 0 noktasındaki f (x) türevine, fonksiyonun artışının argümanın artışına oranının limiti denir, burada ∆ x → 0 ise bunu f (x 0) = lim ∆ x → 0 ∆ y ∆ x olarak gösteririz.

Bundan f " (x 0) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x olduğu sonucu çıkar; burada k x, teğetin eğimi olarak gösterilir.

Yani, f' (x)'in x 0 noktasında var olabileceğini ve fonksiyonun belirli bir grafiğine teğetinin x 0, f 0 (x 0)'a eşit olduğu noktada var olabileceğini bulduk; Teğetin bu noktadaki eğimi, x 0 noktasındaki türevine eşittir. O zaman şunu elde ederiz: k x = f " (x 0) .

Bir fonksiyonun bir noktadaki türevinin geometrik anlamı, grafiğe aynı noktada bir teğetin varlığı kavramının verilmesidir.

Düzlemdeki herhangi bir doğrunun denklemini yazabilmek için içinden geçtiği noktanın açısal katsayısının bulunması gerekir. Kesişme noktasında gösterimi x 0 olarak alınır.

Y = f (x) fonksiyonunun grafiğine x 0, f 0 (x 0) noktasındaki teğet denklemi y = f "(x 0) x - x 0 + f (x 0) formunu alır.

Bu, f "(x 0) türevinin son değerinin, lim x → x 0 + 0 f " (x) = ∞ ve lim x → x 0 - şartıyla dikey olarak teğetin konumunu belirleyebileceği anlamına gelir - 0 f "(x ) = ∞ veya lim x → x 0 + 0 f " (x) ≠ lim x → x 0 - 0 f " (x) koşulu altında hiç yokluk.

Teğetin konumu açısal katsayısının değerine bağlıdır k x = f "(x 0). O x eksenine paralel olduğunda, o y - k x = ∞'a paralel olduğunda k k = 0 olduğunu ve formunu elde ederiz. tanjant denklemi x = x 0 k x > 0 ile artar, k x olarak azalır< 0 .

Örnek 2

y = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 fonksiyonunun grafiğine (1; 3) koordinatlı noktada teğet için bir denklem derleyin ve eğim açısını belirleyin.

Çözüm

Koşullu olarak, fonksiyonun tüm gerçek sayılar için tanımlandığını biliyoruz. Koordinatları (1; 3) koşuluyla belirtilen noktanın bir teğet noktası olduğunu, bu durumda x 0 = - 1, f (x 0) = - 3 olduğunu buluruz.

-1 değerine sahip noktanın türevini bulmak gerekir. Bunu anlıyoruz

y " = e x + 1 + x 3 3 - 6 - 3 3 x - 17 - 3 3 " = = e x + 1 " + x 3 3 " - 6 - 3 3 x " - 17 - 3 3 " = e x + 1 + x 2 - 6 - 3 3 y " (x 0) = y " (- 1) = e - 1 + 1 + - 1 2 - 6 - 3 3 = 3 3

f'(x)'in teğet noktasındaki değeri, eğimin tanjantına eşit olan teğetin eğimidir.

O zaman k x = t g α x = y " (x 0) = 3 3

Bundan şu sonuç çıkar: α x = a r c t g 3 3 = π 6

Cevap: teğet denklem şu şekli alır

y = f " (x 0) x - x 0 + f (x 0) y = 3 3 (x + 1) - 3 y = 3 3 x - 9 - 3 3

Açıklık sağlamak için grafiksel bir örnekte bir örnek veriyoruz.

Orijinal fonksiyonun grafiğinde siyah renk kullanılmıştır, mavi– teğet görüntüsü, kırmızı nokta – teğet noktası. Sağdaki şekil büyütülmüş bir görünümü göstermektedir.

Örnek 3

Belirli bir fonksiyonun grafiğine bir teğetin varlığını belirleme
y = 3 · x - 1 5 + 1 koordinatları (1 ; 1) olan noktada. Bir denklem yazın ve eğim açısını belirleyin.

Çözüm

Koşullu olarak, belirli bir fonksiyonun tanım tanım kümesinin tüm gerçek sayılar kümesi olarak kabul edildiğini biliyoruz.

Türevini bulmaya geçelim

y " = 3 x - 1 5 + 1 " = 3 1 5 (x - 1) 1 5 - 1 = 3 5 1 (x - 1) 4 5

Eğer x 0 = 1 ise f' (x) tanımsızdır ancak limitler şu şekilde yazılır: lim x → 1 + 0 3 5 1 (x - 1) 4 5 = 3 5 1 (+ 0) 4 5 = 3 5 · 1 + 0 = + ∞ ve lim x → 1 - 0 3 5 · 1 (x - 1) 4 5 = 3 5 · 1 (- 0) 4 5 = 3 5 · 1 + 0 = + ∞, bu şu anlama gelir: (1; 1) noktasında dikey teğetin varlığı.

Cevap: denklem x = 1 formunu alacaktır, burada eğim açısı π 2'ye eşit olacaktır.

Açıklık sağlamak için, bunu grafiksel olarak gösterelim.

Örnek 4

y = 1 15 x + 2 3 - 4 5 x 2 - 16 5 x - 26 5 + 3 x + 2 fonksiyonunun grafiğindeki noktaları bulun; burada

1. Teğet yoktur;
2. Teğet x'e paraleldir;
3. Teğet y = 8 5 x + 4 doğrusuna paraleldir.

Çözüm

Tanımın kapsamına dikkat etmek gerekir. Koşullu olarak, fonksiyonun tüm gerçek sayılar kümesinde tanımlı olduğunu biliyoruz. Modülü genişletip sistemi x ∈ - ∞ aralıklarıyla çözüyoruz; 2 ve [-2; + ∞) . Bunu anlıyoruz

y = - 1 15 x 3 + 18 x 2 + 105 x + 176, x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 , x ∈ [ - 2 ; + ∞)

Fonksiyonu ayırt etmek gerekiyor. Bizde buna sahibiz

y " = - 1 15 x 3 + 18 x 2 + 105 x + 176 " , x ∈ - ∞ ; - 2 1 15 x 3 - 6 x 2 + 9 x + 12 ", x ∈ [ - 2 ; + ∞) ⇔ y " = - 1 5 (x 2 + 12 x + 35) , x ∈ - ∞ ; - 2 1 5 x 2 - 4 x + 3 , x ∈ [ - 2 ; + ∞)

x = - 2 olduğunda türev mevcut değildir çünkü o noktada tek taraflı limitler eşit değildir:

lim x → - 2 - 0 y " (x) = lim x → - 2 - 0 - 1 5 (x 2 + 12 x + 35 = - 1 5 (- 2) 2 + 12 (- 2) + 35 = - 3 lim x → - 2 + 0 y " (x) = lim x → - 2 + 0 1 5 (x 2 - 4 x + 3) = 1 5 - 2 2 - 4 - 2 + 3 = 3

Fonksiyonun değerini x = - 2 noktasında hesaplıyoruz, buradan şunu elde ediyoruz:

1. y (- 2) = 1 15 - 2 + 2 3 - 4 5 (- 2) 2 - 16 5 (- 2) - 26 5 + 3 - 2 + 2 = - 2, yani () noktasındaki teğet - 2; - 2) mevcut olmayacak.
2. Eğim sıfır olduğunda teğet x'e paraleldir. O zaman k x = t g α x = f "(x 0). Yani, fonksiyonun türevi onu sıfıra getirdiğinde böyle bir x'in değerlerini bulmak gerekir. Yani f' değerleri (x), teğetin x'e paralel olduğu teğet noktaları olacaktır.

x ∈ - ∞ olduğunda; - 2, o zaman - 1 5 (x 2 + 12 x + 35) = 0 ve x ∈ (- 2; + ∞) için 1 5 (x 2 - 4 x + 3) = 0 elde ederiz.

1 5 (x 2 + 12 x + 35) = 0 D = 12 2 - 4 35 = 144 - 140 = 4 x 1 = - 12 + 4 2 = - 5 ∈ - ∞ ; - 2 x 2 = - 12 - 4 2 = - 7 ∈ - ∞ ; - 2 1 5 (x 2 - 4 x + 3) = 0 D = 4 2 - 4 · 3 = 4 x 3 = 4 - 4 2 = 1 ∈ - 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ - 2; +∞

İlgili fonksiyon değerlerini hesaplayın

y 1 = y - 5 = 1 15 - 5 + 2 3 - 4 5 - 5 2 - 16 5 - 5 - 26 5 + 3 - 5 + 2 = 8 5 y 2 = y (- 7) = 1 15 - 7 + 2 3 - 4 5 (- 7) 2 - 16 5 - 7 - 26 5 + 3 - 7 + 2 = 4 3 y 3 = y (1) = 1 15 1 + 2 3 - 4 5 1 2 - 16 5 1 - 26 5 + 3 1 + 2 = 8 5 y 4 = y (3) = 1 15 3 + 2 3 - 4 5 3 2 - 16 5 3 - 26 5 + 3 3 + 2 = 4 3

Dolayısıyla - 5; 8 5, -4; 4 3, 1; 8 5, 3; 4 3 fonksiyon grafiğinin gerekli noktaları olarak kabul edilir.

Çözümün grafiksel gösterimine bakalım.

Siyah çizgi fonksiyonun grafiğidir, kırmızı noktalar ise teğet noktalarıdır.

1. Doğrular paralel olduğunda açısal katsayılar eşittir. Daha sonra fonksiyon grafiğinde eğimin 8 5 değerine eşit olacağı noktaları aramanız gerekir. Bunu yapmak için, y "(x) = 8 5 formundaki bir denklemi çözmeniz gerekir. Daha sonra, eğer x ∈ - ∞; - 2 ise, şunu elde ederiz: - 1 5 (x 2 + 12 x + 35) = 8 5 ve eğer x ∈ ( - 2 ; + ∞), o zaman 1 5 (x 2 - 4 x + 3) = 8 5.

Diskriminant sıfırdan küçük olduğundan birinci denklemin kökleri yoktur. Bunu bir kenara yazalım

1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 - 4 43 = - 28< 0

Başka bir denklemin iki gerçek kökü vardır, o zaman

1 5 (x 2 - 4 x + 3) = 8 5 x 2 - 4 x - 5 = 0 D = 4 2 - 4 · (- 5) = 36 x 1 = 4 - 36 2 = - 1 ∈ - 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ - 2; +∞

Fonksiyonun değerlerini bulmaya geçelim. Bunu anlıyoruz

y 1 = y (- 1) = 1 15 - 1 + 2 3 - 4 5 (- 1) 2 - 16 5 (- 1) - 26 5 + 3 - 1 + 2 = 4 15 y 2 = y (5) = 1 15 5 + 2 3 - 4 5 5 2 - 16 5 5 - 26 5 + 3 5 + 2 = 8 3

Değerleri olan puanlar - 1; 4 15, 5; 8 3, teğetlerin y = 8 5 x + 4 doğrusuna paralel olduğu noktalardır.

Cevap: siyah çizgi - fonksiyonun grafiği, kırmızı çizgi - y = 8 5 x + 4'ün grafiği, mavi çizgi - - 1 noktalarındaki teğetler; 4 15, 5; 8 3.

Verilen fonksiyonlar için sonsuz sayıda teğet olabilir.

Örnek 5

y = 3 cos 3 2 x - π 4 - 1 3 fonksiyonunun y = - 2 x + 1 2 düz çizgisine dik olan tüm mevcut teğetlerinin denklemlerini yazın.

Çözüm

Teğet denklemini derlemek için doğruların diklik durumuna göre teğet noktasının katsayısını ve koordinatlarını bulmak gerekir. Tanım şu şekildedir: Düz çizgilere dik açısal katsayıların çarpımı -1'e eşittir, yani k x · k ⊥ = - 1 şeklinde yazılır. Açısal katsayının çizgiye dik olması ve k ⊥ = - 2'ye eşit olması durumunda k x = - 1 k ⊥ = - 1 - 2 = 1 2 olur.

Şimdi temas noktalarının koordinatlarını bulmanız gerekiyor. Belirli bir fonksiyon için x'i ve ardından değerini bulmanız gerekir. Noktadaki türevin geometrik anlamından
x 0 bunu elde ederiz k x = y "(x 0). Bu eşitlikten temas noktaları için x'in değerlerini buluruz.

Bunu anlıyoruz

y " (x 0) = 3 çünkü 3 2 x 0 - π 4 - 1 3 " = 3 - sin 3 2 x 0 - π 4 3 2 x 0 - π 4 " = = - 3 sin 3 2 x 0 - π 4 3 2 = - 9 2 günah 3 2 x 0 - π 4 ⇒ k x = y " (x 0) ⇔ - 9 2 günah 3 2 x 0 - π 4 = 1 2 ⇒ günah 3 2 x 0 - π 4 = - 1 9

Bu trigonometrik denklem, teğet noktaların koordinatlarını hesaplamak için kullanılacaktır.

3 2 x 0 - π 4 = a r c sin - 1 9 + 2 πk veya 3 2 x 0 - π 4 = π - a r c sin - 1 9 + 2 πk

3 2 x 0 - π 4 = - a r c sin 1 9 + 2 πk veya 3 2 x 0 - π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 - a r c sin 1 9 + 2 πk veya x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z bir tamsayılar kümesidir.

x temas noktası bulundu. Şimdi y'nin değerlerini aramaya devam etmeniz gerekiyor:

y 0 = 3 çünkü 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - sin 2 3 2 x 0 - π 4 - 1 3 veya y 0 = 3 - 1 - sin 2 3 2 x 0 - π 4 - 1 3

y 0 = 3 1 - - 1 9 2 - 1 3 veya y 0 = 3 - 1 - - 1 9 2 - 1 3

y 0 = 4 5 - 1 3 veya y 0 = - 4 5 + 1 3

Bundan 2 3 π 4 - a r c sin 1 9 + 2 πk; 4 5 - 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; - 4 5 + 1 3 teğetlik noktalarıdır.

Cevap: gerekli denklemler şu şekilde yazılacaktır:

y = 1 2 x - 2 3 π 4 - a r c sin 1 9 + 2 πk + 4 5 - 1 3 , y = 1 2 x - 2 3 5 π 4 + a r c sin 1 9 + 2 πk - 4 5 + 1 3 , k ∈ Z

Görsel bir gösterim için, bir fonksiyonu ve bir koordinat çizgisi üzerinde bir teğeti düşünün.

Şekilde fonksiyonun [-10; 10 ], burada siyah çizgi fonksiyonun grafiğidir, mavi çizgiler ise y = - 2 x + 1 2 formunun verilen çizgisine dik olan teğetlerdir. Kırmızı noktalar temas noktalarıdır.

2. dereceden eğrilerin kanonik denklemleri tek değerli fonksiyonlar değildir. Onlar için teğet denklemler bilinen şemalara göre derlenmiştir.

Bir daireye teğet

Merkezi x c e n t e r noktasında olan bir daire tanımlamak için; y c e n t e r ve yarıçap R ise x - x c e n t e r 2 + y - y c e n t e r 2 = R 2 formülünü uygulayın.

Bu eşitlik iki fonksiyonun birleşimi olarak yazılabilir:

y = R 2 - x - x c e n t e r 2 + y c e n t e r y = - R 2 - x - x c e n t e r 2 + y c e n t e r

İlk fonksiyon şekilde gösterildiği gibi üstte, ikincisi ise altta bulunur.

x 0 noktasındaki bir çemberin denklemini derlemek için; Üst veya alt yarım daire içinde bulunan y 0, y = R 2 - x - x c e n t e r 2 + y c e n t e r veya y = - R 2 - x - x c e n t e r 2 + formundaki bir fonksiyonun grafiğinin denklemini bulmalısınız. belirtilen noktada y merkezi.

X merkez noktalarındayken; y merkezi + R ve x merkezi; y c e n t e r - R teğetleri, y = y c e n t e r + R ve y = y c e n t e r - R denklemleriyle ve x c ​​e n t e r + R noktalarında verilebilir; y merkez ve
x merkezi r - R ; y c e n t e r, y'ye paralel olacaktır, o zaman x = x c e n t e r + R ve x = x c e n t e r - R biçiminde denklemler elde ederiz.

Bir elipse teğet

Elipsin xmerkezde bir merkezi olduğunda; y c e n t e r yarı eksenleri a ve b ile, bu durumda x - x c e n t e r 2 a 2 + y - y c e n t e r 2 b 2 = 1 denklemi kullanılarak belirtilebilir.

Bir elips ve bir daire, üst ve alt yarım elips olmak üzere iki fonksiyonun birleştirilmesiyle gösterilebilir. O zaman bunu anlıyoruz

y = b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r y = - b a · a 2 - (x - x c e n t e r) 2 + y c e n t e r

Teğetler elipsin köşelerinde bulunuyorsa, x veya y civarında paraleldirler. Aşağıda, netlik sağlamak için şekli düşünün.

Örnek 6

X değerlerinin x = 2'ye eşit olduğu noktalarda x - 3 2 4 + y - 5 2 25 = 1 elipsine teğet denklemini yazın.

Çözüm

x = 2 değerine karşılık gelen teğet noktaları bulmak gerekir. Elipsin mevcut denklemini yerine koyarız ve şunu buluruz:

x - 3 2 4 x = 2 + y - 5 2 25 = 1 1 4 + y - 5 2 25 = 1 ⇒ y - 5 2 = 3 4 25 ⇒ y = ± 5 3 2 + 5

Sonra 2; 5 3 2 + 5 ve 2; - 5 3 2 + 5 üst ve alt yarım elipse ait teğet noktalardır.

Elipsin denklemini y'ye göre bulma ve çözmeye geçelim. Bunu anlıyoruz

x - 3 2 4 + y - 5 2 25 = 1 y - 5 2 25 = 1 - x - 3 2 4 (y - 5) 2 = 25 1 - x - 3 2 4 y - 5 = ± 5 1 - x - 3 2 4 y = 5 ± 5 2 4 - x - 3 2

Açıkçası, üst yarı elips y = 5 + 5 2 4 - x - 3 2 ve alt yarı elips y = 5 - 5 2 4 - x - 3 2 formundaki bir fonksiyon kullanılarak belirtilir.

Bir fonksiyonun grafiğine bir noktadaki teğet için bir denklem oluşturmak için standart bir algoritma uygulayalım. 2 noktasındaki ilk teğet için denklemi yazalım; 5 3 2 + 5 şöyle görünecek

y " = 5 + 5 2 4 - x - 3 2 " = 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = - 5 2 x - 3 4 - ( x - 3 ) 2 ⇒ y " (x 0) = y " (2) = - 5 2 2 - 3 4 - (2 - 3) 2 = 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = 5 2 3 (x - 2) + 5 3 2 + 5

İkinci teğetin denkleminin bu noktada bir değerle olduğunu buluyoruz.
2; - 5 3 2 + 5 formunu alır

y " = 5 - 5 2 4 - (x - 3) 2 " = - 5 2 1 2 4 - (x - 3) 2 4 - (x - 3) 2 " = = 5 2 x - 3 4 - (x - 3) 2 ⇒ y " (x 0) = y " (2) = 5 2 2 - 3 4 - (2 - 3) 2 = - 5 2 3 ⇒ y = y " (x 0) x - x 0 + y 0 ⇔ y = - 5 2 3 (x - 2) - 5 3 2 + 5

Grafiksel olarak teğetler aşağıdaki gibi gösterilir:

Abartıya teğet

Bir hiperbolün merkezi x merkezde olduğunda; y merkezi ve köşeler x merkezi + α ; y merkezi ve x merkezi - α ; y c e n t e r eşitsizliği x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = 1, köşeleri x c e n t e r ise; y merkezi + b ve x merkezi; y c e n t e r - b , bu durumda x - x c e n t e r 2 α 2 - y - y c e n t e r 2 b 2 = - 1 eşitsizliği kullanılarak belirtilir .

Bir hiperbol, formun iki birleşik fonksiyonu olarak temsil edilebilir

y = b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r y = - b a · (x - x c e n t e r) 2 - a 2 + y c e n t e r veya y = b a · (x - x c e n t e r) 2 + a 2 + y ce n t e r y = - b a · (x - x merkezi) 2 + a 2 + y merkezi

İlk durumda teğetlerin y'ye paralel olduğunu, ikinci durumda ise x'e paralel olduklarını görüyoruz.

Bir hiperbolün teğet denklemini bulmak için teğet noktasının hangi fonksiyona ait olduğunu bulmak gerekir. Bunu belirlemek için denklemlerde yerine koyma ve özdeşliği kontrol etmek gerekir.

Örnek 7

7 noktasında x - 3 2 4 - y + 3 2 9 = 1 hiperbolüne teğet için bir denklem yazın; - 3 3 - 3 .

Çözüm

Bir hiperbolün bulunması için çözüm kaydını 2 fonksiyon kullanarak dönüştürmek gerekir. Bunu anlıyoruz

x - 3 2 4 - y + 3 2 9 = 1 ⇒ y + 3 2 9 = x - 3 2 4 - 1 ⇒ y + 3 2 = 9 x - 3 2 4 - 1 ⇒ y + 3 = 3 2 x - 3 2 - 4 ve y + 3 = - 3 2 x - 3 2 - 4 ⇒ y = 3 2 x - 3 2 - 4 - 3 y = - 3 2 x - 3 2 - 4 - 3

Koordinatları 7 olan belirli bir noktanın hangi fonksiyona ait olduğunu belirlemek gerekir; - 3 3 - 3 .

Açıkçası, ilk fonksiyonu kontrol etmek için y (7) = 3 2 · (7 - 3) 2 - 4 - 3 = 3 3 - 3 ≠ - 3 3 - 3 gereklidir, bu durumda nokta grafiğe ait değildir, çünkü eşitlik sağlanamıyor.

İkinci fonksiyon için elimizde y (7) = - 3 2 · (7 - 3) 2 - 4 - 3 = - 3 3 - 3 ≠ - 3 3 - 3 bulunur, bu da noktanın verilen grafiğe ait olduğu anlamına gelir. Buradan eğimi bulmalısınız.

Bunu anlıyoruz

y " = - 3 2 (x - 3) 2 - 4 - 3 " = - 3 2 x - 3 (x - 3) 2 - 4 ⇒ k x = y " (x 0) = - 3 2 x 0 - 3 x 0 - 3 2 - 4 x 0 = 7 = - 3 2 7 - 3 7 - 3 2 - 4 = - 3

Cevap: teğet denklem şu şekilde temsil edilebilir:

y = - 3 x - 7 - 3 3 - 3 = - 3 x + 4 3 - 3

Açıkça şu şekilde tasvir edilmiştir:

Bir parabole teğet

X 0, y (x 0) noktasında y = a x 2 + b x + c parabolüne teğet için bir denklem oluşturmak için standart bir algoritma kullanmanız gerekir, o zaman denklem y = y "(x) formunu alacaktır 0) x - x 0 + y ( x 0) Tepe noktasındaki böyle bir teğet x'e paraleldir.

x = a y 2 + b y + c parabolünü iki fonksiyonun birleşimi olarak tanımlamalısınız. Bu nedenle denklemi y için çözmemiz gerekiyor. Bunu anlıyoruz

x = a y 2 + b y + c ⇔ a y 2 + b y + c - x = 0 D = b 2 - 4 a (c - x) y = - b + b 2 - 4 a (c - x) 2 a y = - b - b 2 - 4 a (c - x) 2 a

Bunu grafiksel olarak şu şekilde gösterelim:

Bir x 0, y (x 0) noktasının bir fonksiyona ait olup olmadığını bulmak için standart algoritmaya göre yavaşça ilerleyin. Böyle bir teğet, parabole göre y'ye paralel olacaktır.

Örnek 8

Teğet açımız 150° olduğunda x - 2 y 2 - 5 y + 3 grafiğine teğetin denklemini yazın.

Çözüm

Çözüme parabolü iki fonksiyon olarak temsil ederek başlıyoruz. Bunu anlıyoruz

2 y 2 - 5 y + 3 - x = 0 D = (- 5) 2 - 4 · (- 2) · (3 - x) = 49 - 8 x y = 5 + 49 - 8 x - 4 y = 5 - 49 - 8 x - 4

Eğimin değeri bu fonksiyonun x 0 noktasındaki türevinin değerine ve eğim açısının tanjantına eşittir.

Şunu elde ederiz:

k x = y " (x 0) = t g α x = t g 150 ° = - 1 3

Buradan temas noktaları için x değerini belirliyoruz.

İlk fonksiyon şu şekilde yazılacaktır:

y " = 5 + 49 - 8 x - 4 " = 1 49 - 8 x ⇒ y " (x 0) = 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3

Açıkçası, negatif bir değere sahip olduğumuz için gerçek kökler yok. Böyle bir fonksiyon için 150° açıya sahip bir teğetin olmadığı sonucuna varıyoruz.

İkinci fonksiyon şu şekilde yazılacaktır:

y " = 5 - 49 - 8 x - 4 " = - 1 49 - 8 x ⇒ y " (x 0) = - 1 49 - 8 x 0 = - 1 3 ⇔ 49 - 8 x 0 = - 3 x 0 = 23 4 ⇒ y (x 0) = 5 - 49 - 8 23 4 - 4 = - 5 + 3 4

Temas noktalarımızın 23 4 olduğunu biliyoruz; - 5 + 3 4 .

Cevap: teğet denklem şu şekli alır

y = - 1 3 x - 23 4 + - 5 + 3 4

Grafiksel olarak şu şekilde gösterelim:

Metinde bir hata fark ederseniz, lütfen onu vurgulayın ve Ctrl+Enter tuşlarına basın.