Pratik iş
matematik
1. Bir fonksiyonun limitini bulma. Birinci ve ikinci harika sınırlardır.
2. Karmaşık bir fonksiyonun türevi. Tek değişkenli bir fonksiyonun incelenmesi ve grafiklerinin çizilmesi.
3. “Fonksiyon çalışmalarına diferansiyel hesabın uygulanması” testi.
4. Belirsiz integrallerin bulunması. Belirli integrallerin hesaplanması.
5. Belirleyicilerin hesaplanması.
6. Doğrusal denklem sistemlerini Cramer yöntemini kullanarak çözme. Ölçek.
7. “Kümeler” konusundaki problemlerin çözümü. Mantıksal cebir formülleri.
8. Rastgele olayların olasılıklarının hesaplanması. Toplam olasılık formülü.
9. Sayısal özelliklerin hesaplanması.
10. Test “Olasılık teorisi ve matematiksel istatistiğin temelleri”
11. Karmaşık bir sayının trigonometrik formu.
12. Karmaşık sayılarla çeşitli şekillerdeki eylemler.
MATEMATİKTE PRATİK ÇALIŞMALAR İÇİN METODOLOJİK TALİMATLAR
KURS 2
Uygulamalı ders, öğrencilerin bir öğretmenin rehberliğinde bir ödev üzerinde bir veya daha fazla pratik çalışma yapmasını içeren eğitim sürecini organize etmenin bir şeklidir.
Böylece matematikteki uygulamalı derslerde öğrenciler, gelecekte özel disiplinlerdeki mesleki problemleri çözmek için kullanılması gereken problem çözme yeteneğini geliştirirler.
Pratik çalışma sırasında öğrenciler bilgi kaynaklarını kullanma, düzenleyici belgeler ve öğretim materyalleri, referans kitapları ile çalışma, çizimler, diyagramlar, tablolar yapma, çeşitli problemleri çözme, hesaplamalar yapma becerisinde ustalaşırlar.
Matematikte uygulamalı derslerde çözülen problemler:
1) dersler sırasında edinilen matematikte teorik bilginin genişletilmesi ve pekiştirilmesi;
2) öğrencilerde matematik problemlerini başarılı bir şekilde çözmek için gerekli pratik beceri ve yetenekleri geliştirmek;
3) öğrencilerin matematik eğitimi sürecinde kendi kendine eğitim ihtiyaçlarının geliştirilmesi ve bilgi ve becerilerin geliştirilmesi;
4) matematik eğitimi sürecinde yaratıcı bir tutum ve araştırma yaklaşımının oluşturulması;
5) gelecekteki bir uzmanın mesleki açıdan önemli niteliklerinin ve edinilen bilgilerin mesleki alanda uygulanmasına ilişkin becerilerin oluşturulması.
Pratik ders No. 1. Fonksiyon sınırlarının hesaplanması. Birinci ve ikinci harika sınırlardır.
Ders : Fonksiyon sınırlarının hesaplanması.
Hedef: Matematiğin temel dalları alanında temel bilgilerin edinilmesi . Fonksiyonların limitlerinin hesaplanmasına ilişkin bilginin özümsenmesinin test edilmesi. Bu konuyla ilgili bilgileri tekrarlayın ve sistemleştirin.
Görevler:
Yaratıcı profesyonel düşüncenin geliştirilmesi;
Bilim diline hakimiyet, kavramları kullanma becerisi;
Problem kurma ve çözme becerilerine hakim olmak;
Teorik ve pratik eğitimin derinleştirilmesi;
Öğrencilerin inisiyatif ve bağımsızlığının geliştirilmesi.
Bilgisayar becerilerinin güçlendirilmesi;
Matematiksel konuşma üzerinde çalışmaya devam edin.
Bağımsız çalışma için becerilerin oluşturulması, bir ders kitabıyla çalışma, bağımsız olarak bilgi edinme becerileri;
Metinle çalışırken ana şeyi vurgulama yeteneğinin geliştirilmesi;
Bağımsız düşünmenin oluşumu, zihinsel işlemler: karşılaştırma, analiz, sentez, genelleme, benzetme;
Öğrencilere, görevleri tamamlama kültürü üzerinde bilginin gücünü derinleştirmek ve artırmak için sistematik çalışmanın rolünü gösterin;
Öğrencilerin yaratıcı yeteneklerinin geliştirilmesi.
Pratik çalışma sağlamak:
Pratik çalışma için metodolojik önerilerin teorik materyali.
Matematik, – Seri: Orta mesleki eğitim. - Rostov-on-Don “Phoenix”, s.
Pratik dersin ilerlemesi.
1.Ders konusunun oluşturulması, konunun akademik disiplinin diğer konularıyla bağlantısının açıklanması;
2.Öğrencilerin derse hazır olup olmadıklarının kontrol edilmesi;
3. Dersin konusuna ve disiplinin çalışma programına uygun olarak işlenmesi:
“Fonksiyonların limitlerinin hesaplanması” konulu teorik materyali inceleyin.
Tipik görevleri çözme örneklerini düşünün.
Birinci ve ikinci dikkate değer limitleri kullanarak fonksiyonların limitlerini hesaplamak için bağımsız çalışmalar yapın.
Güvenlik sorularını cevapla.
Teorik bilgiler ve metodolojik öneriler
problem çözme konusunda.
1. Teorik materyalin sunumu.
Bir fonksiyonun bir noktadaki limitini hesaplamak için şunları yapmanız gerekir:
1) x değişkeni yerine x'in eğilimini yazın.
2) 1. adımı tamamladıktan sonra https://pandia.ru/text/78/405/images/image003_6.png" width="19" height="22 src=">formunda bir belirsizlik alırsak ve değiştirin eksi olan ok: (x-a).
3) 1. adımı tamamladıktan sonra https://pandia.ru/text/78/405/images/image002_13.png" width="18" height="31 src="> şeklinde bir belirsizlik alırsak Trigonometrik fonksiyonların değerleri ile ilgili olarak ilk dikkate değer limiti kullanmalıyız.
Tanım. Dikkate değer ilk limite limit denir
https://pandia.ru/text/78/405/images/image007_4.png" alt="$\displaystyle \lim_(x\to0)\dfrac(\sin x)(x)=1. $" width="102" height="52">!}
5) Tanım:İkinci dikkat çekici sınır limit denir

Bu limitin verdiği sayı hem matematiksel analizlerde hem de matematiğin diğer dallarında oldukça önemli bir rol oynamaktadır. Numara aranır doğal logaritmanın tabanı ( https://pandia.ru/text/78/405/images/image009_4.png" alt="$ e$" width="11" height="14">показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:!}
![]()
2. Çalışılan materyalin konsolidasyonu.
örnek 1
https://pandia.ru/text/78/405/images/image015_1.png" genişlik = "28" yükseklik = "30 src = ">= -4
Kural 1)'i kullandık ve x yerine x'in çabalaması gereken şeyi koyduk, yani x=2.
Örnek 2
https://pandia.ru/text/78/405/images/image017_1.png" genişlik = "154" yükseklik = "32 src = ">.png" genişlik = "21" yükseklik = "30 src = ">= 5
Örnek 3
https://pandia.ru/text/78/405/images/image021_1.png" genişlik = "199" yükseklik = "37 src = ">.png" genişlik = "137" yükseklik = "35 src = ">. png" genişlik = "138" yükseklik = "24 src = ">=3+3=6
Örnek 4
https://pandia.ru/text/78/405/images/image004_7.png" genişlik = "22" yükseklik = "31 src = ">.png" genişlik = "104" yükseklik = "46 src = ">. png" yükseklik = "30 kaynak = ">
Örnek 5
https://pandia.ru/text/78/405/images/image032_0.png" width = "61" height = "46 src = ">.png" height = "30 src = ">=2
Örnek 6
https://pandia.ru/text/78/405/images/image036_0.png" genişlik = "18" yükseklik = "28 src = ">
B) 
V) 
3. Bilgi, beceri ve yeteneklerin pekiştirilmesi.
Fonksiyonların limitlerinin hesaplanması konusunda bağımsız çalışmalar yapın.
Pratik çalışma No. 1. seçenek 1 Fonksiyonun limitini hesaplayın: 1. 2. 3. 10. | Pratik çalışma No. 1. seçenek 2 Fonksiyonun limitini hesaplayın: 1. 2. 3. 10. |
Pratik çalışma No. 2.
Ders : Bir fonksiyonun türevini bulma. Tek değişkenli bir fonksiyonun incelenmesi ve grafiğinin çizilmesi.
Hedef : Bir fonksiyonun türevi kavramı hakkında pratik bilgi testi, temel fonksiyonların türevlerini bulma becerisi, karmaşık fonksiyonlar, ters fonksiyonlar, türev tablosunu ve türev alma kurallarını kullanma, karmaşık ve ters fonksiyon kavramı, beceri Fonksiyonları incelemek için bir türev kullanmak.
Pratik çalışma sağlamak:
Ders kitabı. "Matematik". – M.: Bustard, 2010.
Matematik. M: Forum-İnfa 2008.
Pratik çalışma seçeneğine sahip bireysel kartlar.
1. Bir fonksiyonun türevini bulmanın teorik materyali ve örnekleri.
Tanım: f(x) (f"(x)) fonksiyonunun x noktasındaki türevi, argümanın artışı sıfıra yaklaştığında, fonksiyonun artışının argümanın artışına oranının limitidir:
https://pandia.ru/text/78/405/images/image061_0.png" width="209 height=235" height="235">
Farklılaşma kuralları.
Eğer f(x) ve g(x) fonksiyonlarının türevleri varsa, o zaman
2. (u+v)'=u'+v'
3. (uv)'=u′v+v′u
4. (C u)'=C u', burada C=sabit
5..png" genişlik = "49" yükseklik = "54 src = ">
6. Karmaşık bir fonksiyonun türevi:
f'(g(x))=f'(g) g'(x)
2. Örnekler.
1..png" genişlik = "61" yükseklik = "41 src = ">.png" genişlik = "20" yükseklik = "41 src = ">.png" genişlik = "20" yükseklik = "41 src = "> .png" genişlik = "69" yükseklik = "41 src = ">+4).
İşlev iki faktörün çarpımıdır: u=https://pandia.ru/text/78/405/images/image071_0.png" width="72" height="41 src=">.png" width=" 64" height = "41 src = ">.png" width = "19" height = "41 src = ">.png" width = "45" height = "51 src = ">.
İşlev, iki ifadenin bölümüdür: u=https://pandia.ru/text/78/405/images/image079.png" width = "52" height = "41 src = ">..png" width= "215" " height = "57 src = ">.png" width = "197 yükseklik = 36" yükseklik = "36">
Çözüm. Karmaşık fonksiyonların türev alma kuralını (formül 6) kullanarak bu fonksiyonun türevini bulalım:

5. Eğer öyleyse 
6. sen = X 3 – 3X 2 + 5X+ 2. Hadi bulalım sen "(–1).
sen " = 3X 2 – 6X+ 5. Bu nedenle, sen "(–1) = 14.
7. Eğer sen= günlük Xçünkü X, O sen" = (in X)"çünkü X+in X(çünkü X) " =1/X∙çünkü X–n X günah X.
Bir fonksiyon verilsin. Çalışmak için ihtiyacınız olan:
1) Tanım alanını bulun. Çok zor değilse aralığını da bulmakta fayda var. (Ancak çoğu durumda bulma sorunu fonksiyonun ekstremum değerleri bulunana kadar ertelenir.)
2) Fonksiyonun davranışını belirlemeye yardımcı olacak genel özelliklerini öğrenin: fonksiyonun çift mi, tek mi, periyodik mi olduğu.
3) Eğer böyle sınır noktaları varsa, argüman tanım kümesinin sınır noktalarına yaklaştığında fonksiyonun nasıl davrandığını öğrenin. Bir fonksiyonun süreksizlik noktaları varsa, bu noktaların fonksiyonun düşey asimptotlarının varlığı açısından da kontrol edilmesi gerekir. Eğik asimptotları bulun.
4) Grafiğin koordinat eksenleriyle kesişme noktalarını bulun; bu, yalnızca aşağıdaki koşul altında fonksiyonun değerinin hesaplanmasından oluşur:
OX ekseni ile: y=0;
OY ekseni ile: x=0.
Eksenle kesişme noktalarının bulunması, belki de yalnızca yaklaşık olarak yapılabilecek karmaşık bir cebirsel denklemin çözülmesi ihtiyacına yol açabilir. Fonksiyonun köklerini ve süreksizlik noktalarını bulduktan sonra, bu noktalar arasındaki aralıkların her birinde fonksiyonun işaretini belirleyebiliriz. Bu, fonksiyonun değerini aralığın herhangi bir noktasında hesaplayarak veya aralık yöntemini kullanarak yapılabilir.
5) Monotonluk aralıklarını bulun. Bunu yapmak için türevi bulun ve eşitsizliği çözün:
https://pandia.ru/text/78/405/images/image089.png" width = "49" height = "19 src = ">, fonksiyon azalıyor.
Monotonluk aralıklarını bulduktan sonra, yerel ekstremum noktalarını hemen belirleyebiliriz: bir artışın bir azalma ile değiştirildiği yerde, yerel maksimumlar yerleştirilir ve bir azalmanın bir artışla değiştirildiği yerde, yerel minimumlar yerleştirilir.
6) Dışbükeylik ve içbükeylik aralıklarının bulunması, aralıklarda ikinci türev..png" width="39" height="19 src="> kullanılarak gerçekleştirilir:
https://pandia.ru/text/78/405/images/image090.png" width = "39" height = "19 src = ">‹0 ise, fonksiyon grafiği eğrisi dışbükeydir.
Aynı zamanda bükülme noktalarını, fonksiyonun dışbükeylik yönünü değiştirdiği (ve sürekli olduğu) noktalar olarak tanımlarız.
7) Grafiğin asimptot ve ek noktalarla kesişme noktalarını bulmak. Bu nokta zorunlu değildir ancak bu tür noktaların bulunması, fonksiyonun ve grafiğinin incelenmesini tam ve eksiksiz hale getirir.
Çizimdeki fonksiyonların incelenmesi sırasında elde edilen noktaları koordinat eksenleri ve grafik üzerinde hemen çizmenin yararlı olduğunu unutmayın. Bu, yol boyunca grafiğin görünümünü anlamaya yardımcı olur.
3. Kendiniz yapın:
|
seçenek | y fonksiyonunun türevini bulun: |
seçenek | y fonksiyonunun türevini bulun: |
1.y=6- | 1. y=-6- 5.y= |
||
1.y=-7-1 | 1.y=-7-1 |
||
1.y=4x-3tgx+6x-8 | 1.y=-5x+2ctgx+3x-2 |
||
Dersin Hedefleri:
eğitici- türev alma formüllerini bilir; farklılaşma kuralları;
karmaşık bir fonksiyonun farklılaşması; türevin fiziksel ve geometrik anlamı;
Bir fonksiyonun grafiğine teğet denklemi.
Gelişimsel - Fonksiyonların türevlerini bulabilme; fiziksel anlamı, geometrik anlamı kullanarak problemleri çözebilir; bir fonksiyonun bir noktadaki türevinin değerini bulma; Gerçekleştirilen eylemleri matematiksel olarak doğru bir şekilde açıklayın ve gerekçelendirin.
Eğitici – Bağımsızlığı, sorumluluğu ve düşünmeyi geliştirin.
Dersler sırasında
I. Organizasyon anı.
II. Ödev kontrol ediliyor
(molalar sırasında danışmanlar (öğrencileri) kontrol eder ve not verir).
III. Hedef belirleme ve motivasyon
Öğretmen öğrencilere bu dersin “Türevlerin hesaplanması” konusundaki son ders olduğunu bildirir ve onları kendi hedeflerini formüle etmeye davet eder.
Öğretmen: "Büyük filozof Konfüçyüs bir keresinde şöyle demişti: "Üç yol bilgiye götürür: Düşünme yolu en asil yoldur, taklit yolu en kolay yoldur ve deneyim yolu en acı yoldur." Dolayısıyla bugün sınıfta her biriniz bu konu hakkında bilgi edinmenin hangi yolunda olduğunu belirleyeceksiniz.
Öğrencilere türev hesaplama konusundaki bilgi ve becerilerini gösterme görevi verilir ve bir ders planı verilir.
Aşama I: Görevi “Hatırla” kartını kullanarak tamamlamak.
(formüller ve farklılaşma kuralları hakkındaki bilgilerin test edilmesi).
Aşama II: Bilginin tekrarlanması ve genelleştirilmesi üzerine sözlü ön çalışma.
Aşama III:“Test tahmini” (bu görevi yerine getirirken danışmanların yardımı kabul edilebilir).
BENAşama V: Pratik bir problemin çözümü.
Aşama V: Bağımsız iş
Çalışma ve ödevlerin I, III, V aşamaları değerlendirilir. Danışmanlar sonuçları kontrol edip değerlendirme tablosuna girerler.
Değerlendirme kriterleri: "5"- 19-20 puan;
"4"- 15-18 puan;
"3"- 10-14 puan.
Bilgiye giden yollar
- Referans bilgilerinin çoğaltılması ve düzeltilmesi
Aşama I.
Hedef: kontrol, formül bilgisinin ve farklılaşma kurallarının öz kontrolü
Hatırlamak! F.I. ___________________________________________________ |
|
Türev |
|
c,c - eksileri T |
|
|
|
|
|
F"(x)+ G"(X) |
|
F(X)* G(X) |
|
|
|
Bu görevin sonunda “Türev Tablosu” kullanılarak bir kendi kendine test gerçekleştirilir. Kartlar doğrulama için danışmanlara teslim edilir (kartlarda düzeltme yapılmasına izin verilmez).
V. Bilginin genelleştirilmesi ve sistemleştirilmesi
Aşama II.
1. Oral frontal çalışma.
A. Bu durum için bir görev oluşturun ve çözün.
![]()
1. Fonksiyonun t = 3 noktasındaki türevinin değerini bulun. (Cevap: 21.)
2. Fonksiyonun grafiğine t = 3 noktasındaki teğet için bir denklem oluşturun. (Cevap: y = 21x-45.).
3. Hareket kanunu formülle veriliyorsa, t=3c anındaki cismin hızını ve ivmesini bulun. (Cevap: 21 m/s, 16 m/s²).
4. Fonksiyonun grafiğine t=3 noktasında çizilen tanjantın açısal katsayısını bulunuz. (Cevap: 21.).
5. Fonksiyonun grafiğine t = 3 noktasındaki teğetin eğim açısının tanjantını bulun ve teğet ile Ox ekseninin pozitif yönü arasındaki açının türünü belirleyin. (Cevap: tgα, α açısı dar açıdır)
B. Fonksiyonların türevlerini bulun

2. Aşama III“Test tahmini”


Bu görevin sonunda nihai cevaplara göre bir öz test yapılır ve testler danışmanlara teslim edilir. (kartlarda düzeltme yapılmasına izin verilmez).
Yanıtlar:
1 seçenek |
||||
seçenek 2 |
- Sorunun çözümü
BENAşama V
İleri düzey bir problemin ön çözümü (çözüm danışmanlar tarafından sınıfla birlikte gerçekleştirilir).
Görev
Hangi parametre değerlerinde A bir fonksiyonun grafiğine teğet ![]()
X ekseni ile kesişme noktalarına çizilen çizgiler kendi aralarında 60°'lik bir açı oluşturuyor mu?

Grafik, X eksenini iki noktada kesen yukarı doğru dalları olan bir paraboldür (durum A=0 problemin anlamını karşılamıyor):
IX. Özetleme ve derecelendirme
1. Sorular: a) Dersin amacına ulaşıldı mı?
b) Hangi aşama en zor görünüyordu?
c) En ilginç olanı neydi?
2. Danışmanlar sonuçları duyurur (yoldaki öğrencilerin sayısı ve isimleri)
taklit, yansıma yolları ve deneyim yolları).
Pratik ders
Ders: Türevlerin bulunması. Türevin fonksiyonların incelenmesine ve grafiklerin çizilmesine uygulanması.
Hedef: Türev hesaplamasında uzmanlaşın, türevi kullanarak bir fonksiyonu keşfetmeyi öğrenin
Eğitim araçları: pratik alıştırmalar için not defterleri, konuyla ilgili sunumlar, İnternet kaynakları.
1. Konularla ilgili teorik materyali düşünün: “Türevleri hesaplama kuralları”, “Bir fonksiyonun ekstremumu”, “Dışbükeylik, içbükeylik. Dönüm noktası."
2. Ödev örneklerini gözden geçirin.
3. 1 numaralı test görevini tamamlayın.
Kontrol soruları:
1. Bir fonksiyonun bir noktadaki maksimumunu (minimumunu) tanımlayın. Maksimum (minimum) noktanın oldukça küçük bir komşuluğunda fonksiyonun artış işareti hakkında ne söylenebilir?
2. Bir fonksiyonun ekstremumunun varlığı için gerekli koşullar nelerdir? Bunların geometrik anlamı nedir?
3. Bir fonksiyonun bir segment üzerindeki en büyük ve en küçük değerlerini bulmanın kuralı nedir?
4. Bir eğrinin dışbükeyliğini (içbükeyliğini) bir aralıkta tanımlayın.
5. Bir eğrinin dışbükeylik ve içbükeylik aralıklarını bulmanın kuralı nedir?
6. Eğrinin dönüm noktası. Onu nasıl bulabilirim?
7. Bir fonksiyonun grafiğini oluşturmak için kullanılan algoritma nedir?
Türevlerin hesaplanmasına ilişkin kurallar
Karmaşık bir fonksiyonun türevi.
Eğer en=ƒ( Ve), u=φ(x), o zaman en¢ ( X)=ƒ¢ (i)·φ¢ (X).
Bir toplamın türevi.
Eğer en(X)=Ve(X)+v (X), O en¢ (X)=Ve¢ (X)+v ¢ (X)
Ürünün türevi.
Eğer y(x)=u(X)· v (X), O en¢ = Ve¢ · v + sen · v ¢ .
Özellikle, ( İle· Ve)¢ =c· Ve¢, yani sabit faktör türev işaretinin altından çıkarılır. Bunu doğrulamak kolaydır
(sen 2 ) ¢ = 2 sen ¢ , (sen 3 ) ¢ =3u 2 sen ¢ , … , (sen N ) ¢ =n·u n–1 sen ¢ .
Bölümün türevi.
Eğer öyleyse  .
.
Türev tablosu
1. (İle)¢ =0
Karmaşık bir fonksiyon için: eğer u=u(x), O:
2. (X)¢ =1
3. (X α )¢ = α · Xα–1, A– herhangi bir gerçek sayı.
 .
.
3. 

4. (A X ) ¢ =a X · içinde A
4. 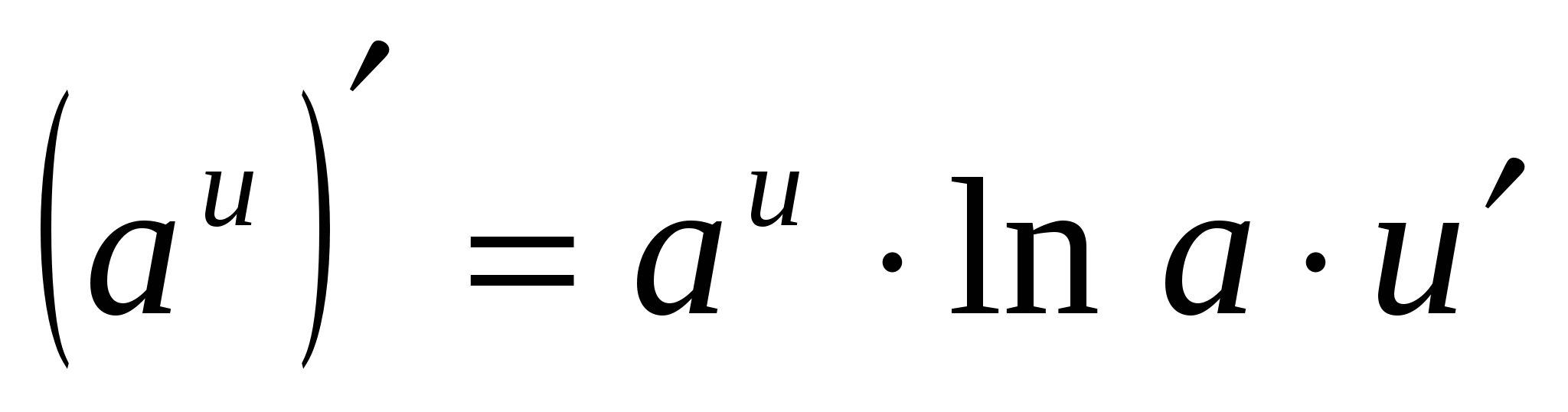

5. (kayıt
A
X)
¢
=
 .
.
5. 

6. (günah x)¢ =çünkü x
6. 
7. (çünkü x)¢ = –sinx
7. 
8. (tgx)¢
=
8. 
9. (ctgx)¢
=
9. 
10. 
10. 
11. 
11. 
12. 
12. 
13. 
13. 
Örnekleri İncele
Örnek 1.
y=(3–2 günah 5x) 4 | Türev formüllerini uyguluyoruz Ve α ,günah sen |
sen ¢ =4·(3–2·sin5x) 3·(3–2sin5x) ¢ =4·(3–2·sin5x) 3 ·(0–2·cos5x·5) = –40·(3–2·sin5x) 3 .
Örnek 2.
. 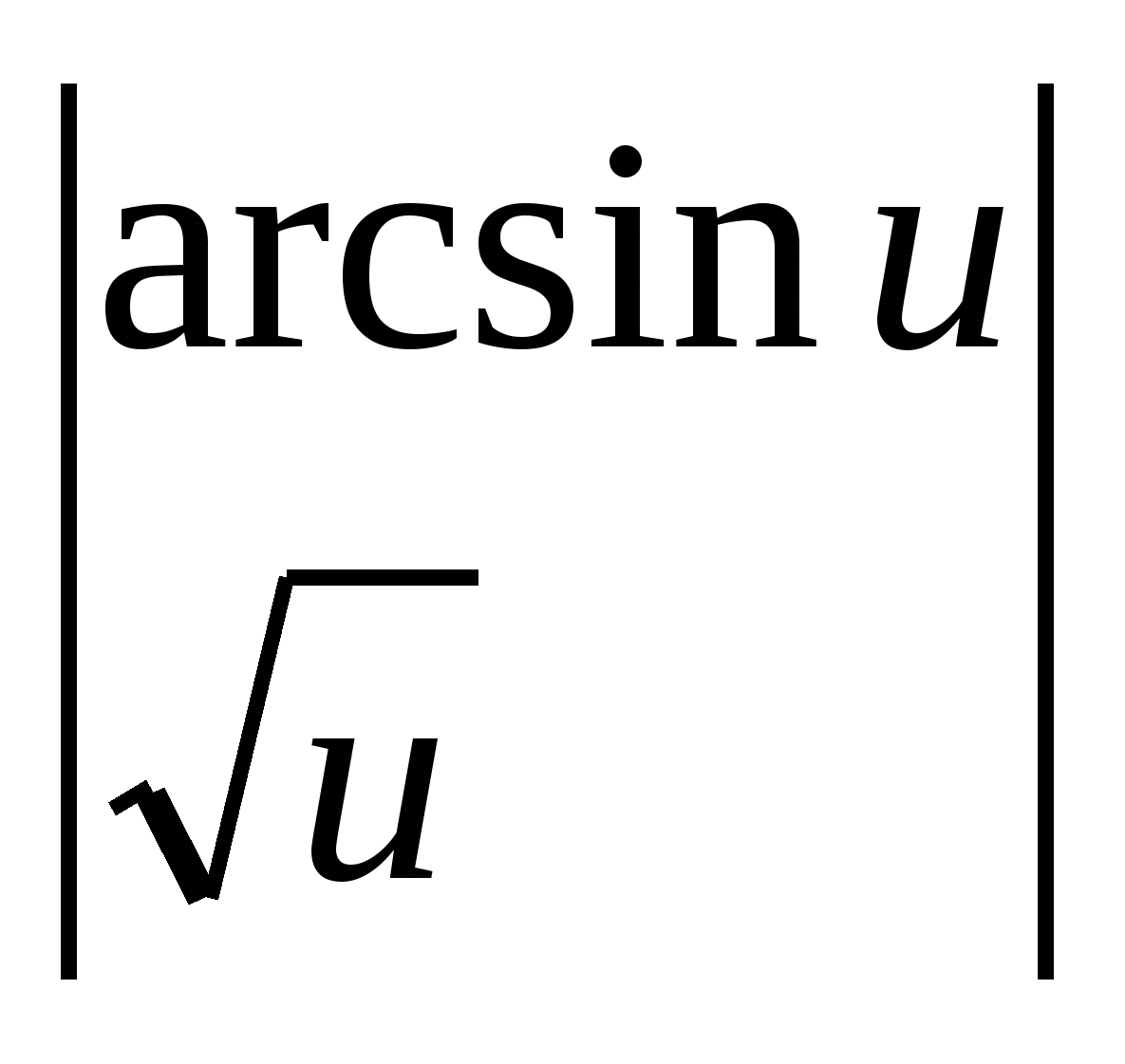

Örnek 3.
 .
. 

Örnek 4.



Örnek 5.
 .
. 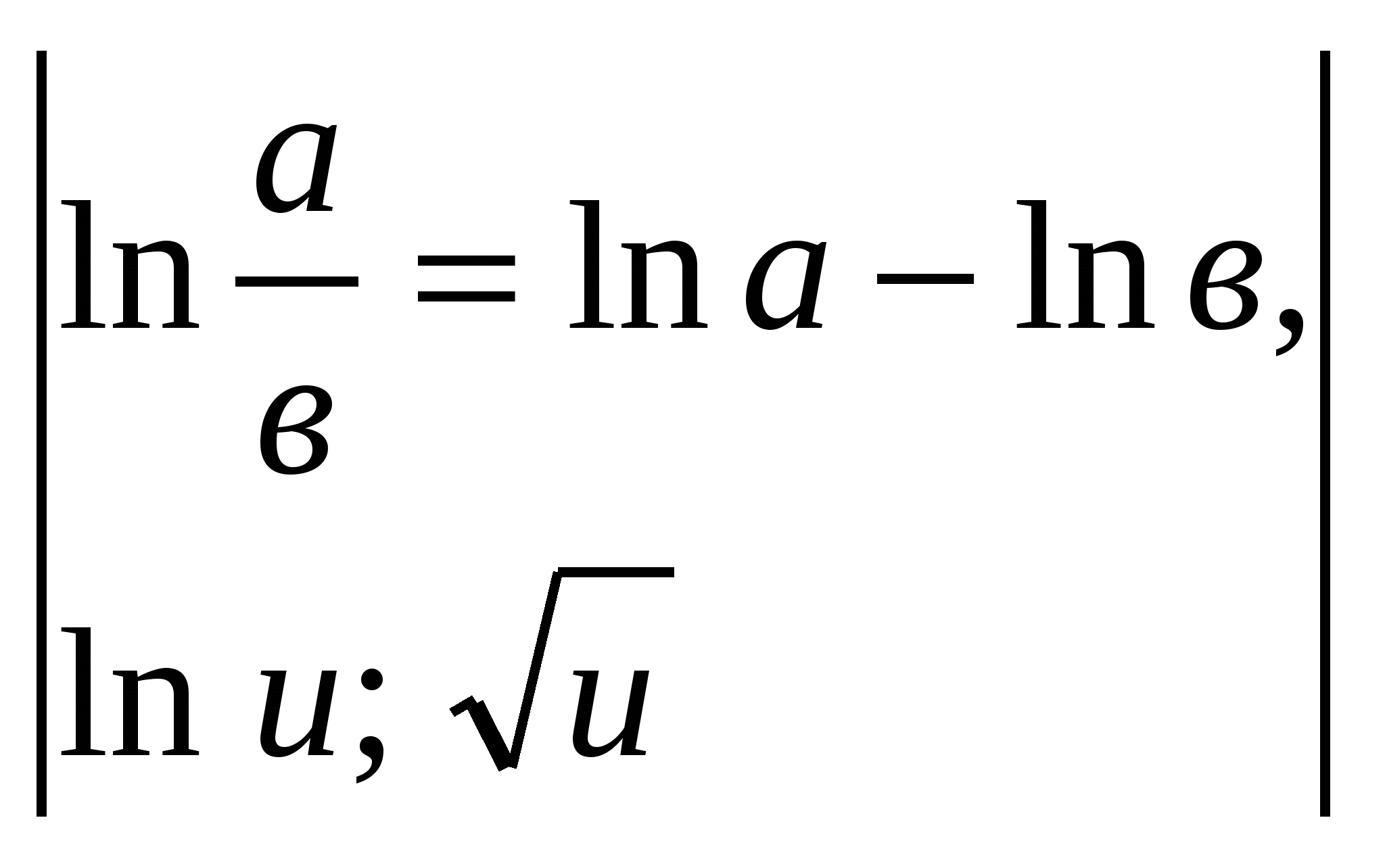

Fonksiyonun ekstremumu
Bir fonksiyonun ekstremumdaki çalışması türevlerin en önemli uygulamalarından biridir. Minima ve maksimumların tanımına ve bunları nasıl bulacağımıza bakalım.
Fonksiyon ƒ( olsun X) belirli bir küme ve bir noktada tanımlanır ve türevlenebilir X 0 onun içindeki bir noktadır.
Tanım.İşlev ƒ (X) noktada X 0 var maksimum(minimum), eğer noktanın böyle bir komşuluğu varsa X 0, herkes içindir X bu alandan ƒ (X) < ƒ (X 0 ) (ƒ (X) > ƒ (X 0 )).
Nokta X 0'a bir nokta denir maksimum(minimum).

Pirinç. 1.
Gösterilen iki maksimum noktaya sahip bir fonksiyonun grafiğidir ( X 1 ve X 3) ve iki minimum puan ( X 2 ve X 4) ve maksimum değer minimumdan daha az olabilir ( ƒ (X 1 ) < ƒ (X 4)). Bu, bir fonksiyonun tekilliğini yalnızca belirli bir noktaya yakın olarak karakterize ettiğimiz gerçeğini vurgulamaktadır.
Fonksiyonun maksimum ve minimum noktalarındaki değerlerine aşırı değerler veya denir. aşırılıklar. Yukarıdaki grafik ekstrem noktaları ( X 1 , X 2 , X 3 , X 4) her birinde türevin belirli bir işareti koruduğu fonksiyonun monotonluk aralıklarını belirler. Ekstrem noktalarda elbette türev sıfıra gider. hakkında bir teorem formüle edelim. gerekli kondisyon bir ekstremun varlığı.
Teorem. Eğer fonksiyon ƒ (X) noktada X 0'ın bir ekstremumu varsa, bu durumda fonksiyonun bu noktadaki türevi sıfıra eşit olur, yani ƒ¢ ( X 0)=0.
Bu koşulun yeterli olmadığını, yani tersinin her zaman doğru olmadığını hemen belirtelim. Eşitlikten ƒ ¢ ( X 0)= 0 mutlaka bu noktada olduğu anlamına gelmez X 0'da bir ekstremum var.
Bu, fonksiyona sahip bir örnekle doğrulanır. ƒ (X)=x 3 .
Bulacağız ƒ ¢ ( X)= 3X 2 . Noktada X=0 ƒ ¢(0)=0 . Ama istediğin kadar noktaya yakın X=0 bulacağız X> 0, burada ƒ (X)=x 3 > 0, bulacağız X< 0, где ¦ (X)=X 3 < 0. Т. е. не существует какая-либо малая окрестность точки X=0, burada herkes için X bir noktadaki fonksiyon değeri X=0 en büyük veya en küçük olacaktır. Bu nedenle nokta X=0 bir ekstrem nokta değildir.
Farklı bir şekilde tartışılabilir. Türevden bu yana ƒ ¢ (x)=3x 2 , ardından fonksiyon ƒ(x)=x 3 herhangi bir gerçek x için artar ve hiçbir ekstremum değeri yoktur.
Gerekli ekstrem koşulun sağlandığı noktalar (ƒ ¢ (x)=0) arandı kritik .
Açıktır ki, fonksiyonun grafiğine şu noktalarda teğettir: ¢ (x)=0, x eksenine paralel Ox .
Yeterli koşul ekstremum aşağıdaki teoremlerde verilmiştir.
Teorem 1. Eğer X 0, fonksiyonun kritik noktasıdır ve buradan geçerken türevin işareti değişir, o zaman X 0 bir ekstrem noktadır, yani türevin işareti artıdan eksiye değişirse maksimum noktadır, işareti eksiden artıya değişirse minimum noktadır.
Türevin işareti değişmiyorsa bir noktada ekstremum olmadığına dikkat edin. Birinci türevi kullanarak ekstremumu incelemenin kuralı okul derslerinden bilinmektedir. Bazen ikinci türevi kullanarak bir ekstremum için yeterli koşulu formüle etmek daha uygundur.
Fonksiyon ƒ( olsun X) bazı etki alanlarında iki kez türevlenebilir (örn. ƒ( X) ƒ¢ ( X) Ve ƒ ¢¢ ( X)).
Teorem 2. Eğer X 0 – fonksiyonun kritik noktası ƒ(x) ve ƒ ¢¢ (X 0 ) > 0 , O X 0 – minimum puan, eğer ƒ ¢¢ (X 0 ) < 0, то X 0 – maksimum nokta.
İkinci türevi kullanarak bir fonksiyonun grafiğinin dışbükeyliği veya içbükeyliği belirlenir.
Dışbükeylik, içbükeylik. Dönüm noktası.
Eğri y=ƒ(X) denir dışbükey olarakbu altında ondan herhangi biri teğet
ƒ ¢¢ ( X) < 0.
Eğri y=ƒ(X) denir içbükey Eğrinin tüm noktalarının uzanması durumunda bir aralıkta daha yüksek ondan herhangi biri teğet bu aralıkta. Daha sonra bu aralıkta
ƒ ¢¢(x) > 0
Tanım. Dönüm noktası eğri, eğrinin bir tarafının dışbükey, diğer tarafının içbükey olduğu bir noktadır.
Bükülme noktasında ƒ ¢¢ ( X)=0.
Dolayısıyla, ikinci türevin işareti (fonksiyonun kendisinin ve birinci türevinin işareti gibi) fonksiyon grafiğinin özelliklerini gösterir. Onlara tekrar bakalım.
Eğer herkes için X aralıkta ( A, B) ƒ (X) > 0 (ƒ (X) < 0), bu durumda grafik x ekseninin üstünde (altında) yer alır.
Eğer herkes için X aralıkta ( A, B) ƒ ¢ ( X) > 0 (ƒ ¢ ( X) < 0), то функция на (A, B) artar (azalır).
Eğer herkes için X aralıkta ( A, B) ƒ ¢¢ ( X) > 0 (ƒ ¢¢ ( X) < 0), то график на (A, B) içbükey (dışbükey).
Denklem ƒ( X)=0, fonksiyonun “sıfırlarını”, yani grafiğin Ox ekseniyle kesişme noktalarını tanımlar.
Denklem ƒ ¢ ( X)=0 kritik noktaları tanımlar.
Denklem ƒ ¢¢ ( X)=0 olası dönüm noktalarını tanımlar.
Fonksiyon çalışma şeması
Fonksiyonu incelemek için ƒ (X) ve çizim y=ƒ(X) bulunmalıdır:
1) fonksiyonun tanım alanı ve grafiğin koordinat eksenleriyle kesişme noktası;
2) monotonluk aralıkları;
3) ekstremum noktaları ve bu noktalardaki fonksiyon değerleri;
4) grafiğin dışbükeylik ve içbükeylik aralıkları;
5) grafiğin dönüm noktaları;
6) elde edilen tüm noktaları (bazen grafiği netleştirmek için ek noktalar elde edilir) ve grafiğin kendisini Kartezyen koordinat sisteminde oluşturun.
Bir fonksiyonun bir segmentteki en küçük ve en büyük değerleri
Optimizasyon yönteminin bazı problemlerini çözerken, belirli bir segment üzerindeki bir fonksiyonun en küçük veya en büyük değerlerini bulabilmek önemlidir. Fonksiyon bu değerlere ya kritik noktalarda ya da parçanın uçlarında ulaşır.
Arama şeması fonksiyonun en küçük ve en büyük değerleri ƒ (X) segmentte [ A, B].
1. Fonksiyonun türevini bulun ƒ ¢ ( X).
2. Denklemin kritik noktalarını bulun ƒ ¢ ( X)=0.
3. Bu segmente ait kritik noktaları seçin [ A, B] ve fonksiyonun değerini bulun ƒ (X) bu tür her noktada.
4. Fonksiyon değerlerini hesaplayın ƒ (X) parçanın uçlarında: ƒ( A) ve ƒ( B).
5. Elde edilen fonksiyon değerlerinden en büyük (en büyük) ve en küçüğünü (en küçük) seçin.
Örnek 2.
Bir fonksiyonun en büyük ve en küçük değerlerini bulma ƒ(x)=X 3 –9x 2 +24х–10 segmentte.
1. ƒ ¢ ( X)= 3X 2 – 9.2 X 2 + 24.
2. ƒ ¢ ( X)=0, 3(X 2 –6X+8)=0, X 1 =2, X 2 =4.
3. x 2 =4 noktası doğru parçasına ait değildir. Bu nedenle fonksiyonun değerini yalnızca şu noktada hesaplıyoruz: X 1 =2
ƒ(2)=2 3 –9·2 2 +24·2–10=10.
4. Parçanın uçlarındaki fonksiyon değerleri: ƒ(0)= –10, ƒ(3)=3 3 –9·3 2 +24·3–10, ƒ(3)=8.
5. Elde edilen değerler:
➡(2)=10, ➡(0)= –10, ➡(3)=8.
En yüksek değer 10 olup şu noktada ulaşılır: X=2. En küçüğü –10'a eşittir ve şu noktada elde edilir: X=0.
Örnek 3.
Eğrinin dışbükeylik ve içbükeylik aralıklarını ve bükülme noktalarını bulun y=x+36X 2 –2X 3 –X 4 .
Bu fonksiyonun tanım alanı tüm gerçek sayılar kümesidir; XЄ(–∞, +∞).
İkinci türevi bulalım.
en¢ =1+72 X–6X 2 –4X 3 .
en¢¢ =72–12 X–12X 2 = –12(X 2 +X–6).
Denklemden. en¢¢ =0 bükülme noktasının apsisini elde ederiz:
–12(X 2 +X–6)=0 X 1 = –3; X 2 =2.
İşareti tanımlayalım en¢¢ aralıklarla
(–∞; –3), (–3; 2), (2, +∞).
X
(–∞, –3)
(–3; 2)
(2; +∞)
en¢¢
eğri şekli
dışbükey
bükülme
içbükey
bükülme
dışbükey
Bükülme noktalarının koordinatlarını bulalım:
en(–3)=726; M 1 (–3; 726) – dönüm noktası
en(2)=114; M 2 (2; 114) – bükülme noktası.
(–3; 2) aralığında eğri içbükeydir. (–∞; –3) ve (2; +∞) aralıklarında – dışbükey.
Ödev örnekleri
Görev No.1.
Fonksiyonun kesme noktalarını bulun ve grafiği çizin

İşlev ƒ (X) tüm gerçekler için tanımlanır X ve belirtilen aralıkların her birinde süreklidir: (–∞; –1), [–1; 0], (0, +∞). Fonksiyonu keşfedelim ƒ (X) noktalarda süreklilik için X= –1 ve X=0.
Bunu yapmak için bu noktaların her birinde tek taraflı limitler bulacağız.

Tek taraflı limitler farklı olduğundan X = –1 – birinci türden süreksizlik noktası.

Tek taraflı limitler eşittir, yani x=0 noktasında fonksiyonun bir limiti vardır ve 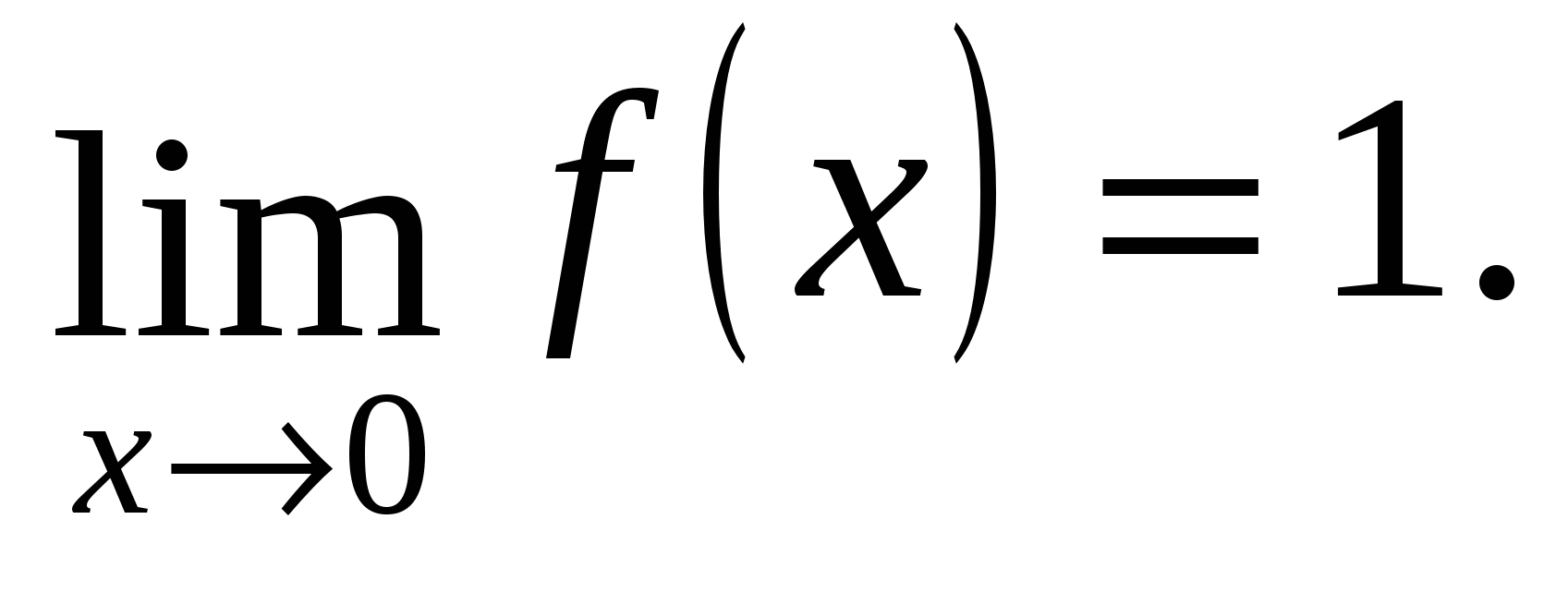
Bu limiti fonksiyonun şu noktadaki değeriyle karşılaştıralım: 
Çünkü  daha sonra x=0'da ƒ(x) fonksiyonu süreklidir.
daha sonra x=0'da ƒ(x) fonksiyonu süreklidir.
Fonksiyonun grafiğini çizelim: (X), verilen
1)  – düz bir çizginin denklemi,
– düz bir çizginin denklemi,
2)  – üst yarım dairenin denklemi
– üst yarım dairenin denklemi  merkez orijinde ve yarıçap birliğe eşit ve –1 £ koşulu altında X£ 0 denklem
merkez orijinde ve yarıçap birliğe eşit ve –1 £ koşulu altında X£ 0 denklem  çeyrek daireyi tanımlar.
çeyrek daireyi tanımlar.
3) için X > 0 grafik denklemle verilir  . Bu eğrinin Ox ekseni ile kesişme noktalarını denklemden buluyoruz
. Bu eğrinin Ox ekseni ile kesişme noktalarını denklemden buluyoruz  x > 0 için. x= π
N, Nerede N
=1, 2, 3, 4,
x > 0 için. x= π
N, Nerede N
=1, 2, 3, 4,

Pirinç. 2.
Görev No.2.
Bir doğruya teğet denklemleri yazın  olduğu noktalarda X=0 ve X=4. Teğetlerin kesişme noktasını ve aralarındaki açıyı bulun. Çizim yapmak.
olduğu noktalarda X=0 ve X=4. Teğetlerin kesişme noktasını ve aralarındaki açıyı bulun. Çizim yapmak.
Bir doğruya teğet denklemi y=ƒ(x) benziyor
Nerede en 0 =ƒ( X 0).
Noktada X=0 en(0)=ƒ(0)=5.
en¢ =ƒ ¢ (X)=X–3 ƒ¢ (0)= –3.
M 1 (0, 5) formuna sahiptir y– 5= –3(X–0) veya
y= –3X+5.
Noktada X=4 en(4)=ƒ(4)=1. ƒ¢ (4)=4–3=1.
Bir noktadaki teğetin denklemi M 2 (4, 1) formuna sahiptir y– 1=X–4 veya
y=x–3.
Sistemi çözerek teğetlerin kesişme noktasını elde ederiz

Kesişim noktası M 3 (2, –1).
Köşe φ formülden bulduğumuz teğetler arasında:
 ,
,
Nerede k 1 = –3; k 2 =1 – teğetlerin açısal katsayıları.
 .
.
Köşe φ = arktg 2.
Bu hattı inşa edelim  – tepe noktasının bulunduğu noktada olan bir parabol X=3, çünkü en¢
=0 saat X=3. Bulacağız
– tepe noktasının bulunduğu noktada olan bir parabol X=3, çünkü en¢
=0 saat X=3. Bulacağız  . Nokta M 4 (3;
. Nokta M 4 (3;  ) parabolün tepe noktasıdır.
) parabolün tepe noktasıdır.
R 
dır-dir. 3.
Görev No.3.
İşlevi keşfedin  ve planlayın.
ve planlayın.
1. Bu fonksiyon bir polinomdur (parantezleri açabilirsiniz, üçüncü dereceden bir polinom elde ederiz), dolayısıyla tanımlanmış, sürekli ve herhangi bir fonksiyon için türevlenebilir X.
2. Türevini bulalım.
 .
.
Denklemden. en¢ =0 kritik noktaları bulalım: 3 X·( X–2)=0, X 1 =0, X 2 =2.
Onları keşfedelim.
X
(–∞, 0)
(0; 2)
(2; +∞)
en ¢
en
3. Yani fonksiyon (–∞, 0) ve (2, +∞) aralıklarında artar, (0; 2) aralığında azalır, x=0'da maksimumu ve x=2'de minimumu vardır:
en maksimum = en(0)=4; en dk = en(2)=0.
4. İkinci türevi bulalım.
en¢¢ = 6·( X-1).
Eğri dışbükeydir, burada en¢¢ < 0, т. е. 6·(X–1) < 0, X < 1.
Eğri içbükeydir, burada en¢¢ > 0, yani X > 1.
Yani (–∞, 1) aralığında eğri dışbükeydir; ve (1, +∞) aralığında içbükeydir.
5. Denklemden dönüm noktasını buluyoruz en¢¢ =0. Böylece, X=1 – bükülme noktasının apsisi, çünkü bu nokta eğrinin dışbükeylik ve içbükeylik aralıklarını ayırır. Bükülme noktası ordinatı: en(1)=2.
Bir fonksiyonun grafiği en=(X+1)·( X–2) 2, Ox eksenini şu noktada keser: en=0, yani ne zaman X= –1 ve X=2;
Oy eksenini keser X=0, yani ne zaman en=4. Üç puan aldık: (–1; 0), (2; 0), (0; 4). Elde edilen tüm noktaları bitişik olanları ekleyerek tabloya gireceğiz.
–2
–1



–16


dır-dir. 4 Eğri y=(x+1)(x–2) 2.
Görev No.1
Size bir, iki, üç veya daha fazla doğru cevabı olabilecek görevler sunuyoruz. Tüm doğru cevapların rakamlarını daire içine alın.
1. Eğer  o zaman fonksiyon
o zaman fonksiyon
1) artan
2) azalan
3) sabit
2. Eğer
1) Artıyor
2) Azalan
3. Eğer  , ardından fonksiyon
, ardından fonksiyon
1) Artıyor
2) Azalan
4. Eğer  , ardından fonksiyon
, ardından fonksiyon
1) Artıyor 3) Azalıyor
2) Sabit 4) Monoton
5. İşlev  Dır-dir
Dır-dir
1) Çift
2) Hatta
3) ne çift ne de tek
4) Periyodik
5) Periyodik değil
6) Trigonometrik
7) İlköğretim
6. İşlev  Dır-dir
Dır-dir
1) çift
2) tek
3) ne çift ne de tek
4) periyodik
5) periyodik değil
6) trigonometrik
7) ilkokul
2) Weierstrass 4) Dirichlet 6) Leibniz
8) Çözüm  Denklemler
Denklemler
1) 0 3) 0 ve 3 5) 2 7) 3
2) 2 ve 3 4) 2 6) -5 ve 1 8) 5 ve 1
9) eşitsizliğin çözümü 
1) ( ; 1) 3) (
; 1) 3) ( ; 1) 5) (-
; 1) 5) (- ;1)
;1)
2) (1; 5) 4) (2;  ) 6)
) 6) 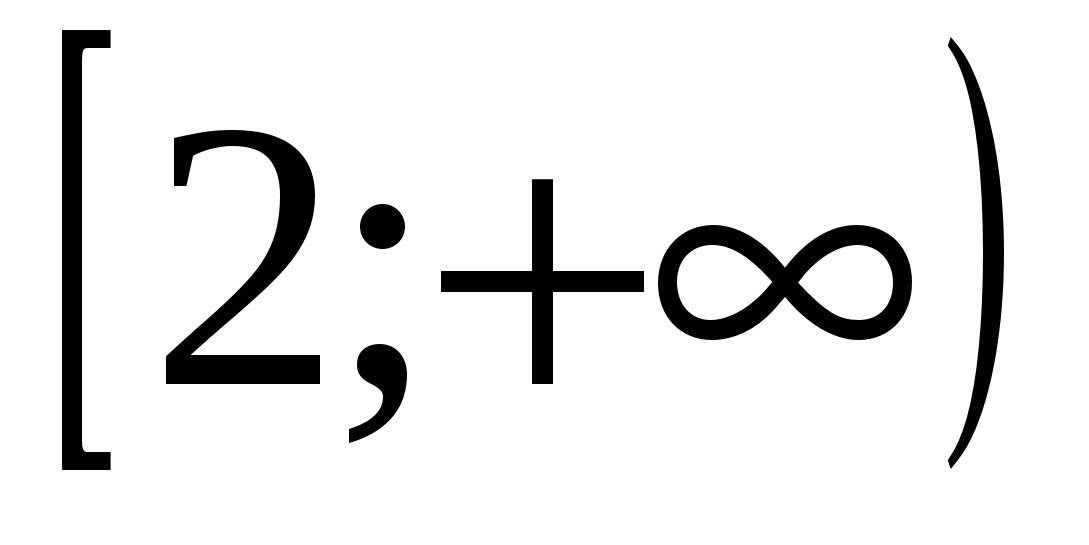
10) Yöntem  Bulunan miktar
Bulunan miktar
1) vektörler
2) düz
3) bölüm
11) Eğer  , ardından fonksiyon
, ardından fonksiyon
1) İçbükey 3) Dışbükey 5) Azalan
2) Monoton 4) Artan 6) Sabit
12) fonksiyonun tanım alanı eşittir 
1) ( ;0)
;0)
2) (0;  )
)
3) (- ;
; )
)
4) (0;1)
5) 
6) 
7) (-1;1)
8) 
9) 
13) işlev  dır-dir
dır-dir
1) gösterge niteliğinde
2) trigonometrik
3) güç
4) logaritmik
14) eğer fonksiyonlar y = X  o zaman o
o zaman o 
1) çift
2) tek
3) ne çift ne de tek
15) işlev  en
en  dır-dir
dır-dir

 .
.



