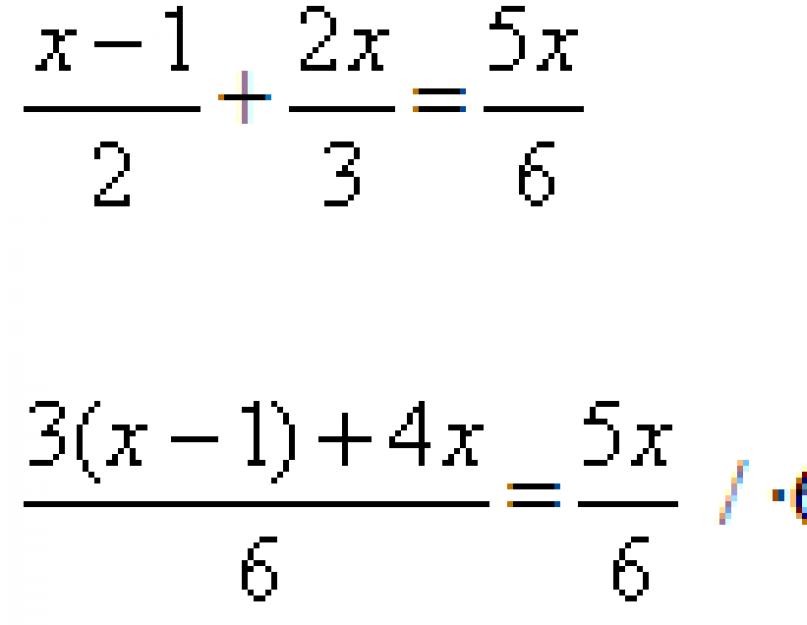"Kesirli rasyonel denklemlerin çözümü"

Dersin Hedefleri:

öğretici:

kesirli rasyonel denklemler kavramının oluşumu; kesirli rasyonel denklemleri çözmenin çeşitli yollarını düşünmek; kesrin sıfıra eşit olması koşulu da dahil olmak üzere kesirli rasyonel denklemleri çözmek için bir algoritma düşünün; kesirli rasyonel denklemlerin algoritmaya göre çözümünü öğretmek; test çalışması yaparak konunun asimilasyon seviyesini kontrol etmek.

Geliştirme:

edinilen bilgilerle doğru bir şekilde çalışma, mantıklı düşünme yeteneğinin geliştirilmesi; entelektüel becerilerin ve zihinsel işlemlerin gelişimi - analiz, sentez, karşılaştırma ve genelleme; inisiyatif geliştirme, karar verme yeteneği, orada durmamak; eleştirel düşünmenin gelişimi; araştırma becerilerinin geliştirilmesi.

beslemek:

konuya bilişsel ilgi eğitimi; eğitim sorunlarının çözümünde bağımsızlık eğitimi; nihai sonuçlara ulaşmak için irade ve azim eğitimi.

ders türü: ders - yeni materyalin açıklaması.

Dersler sırasında

1. Organizasyonel an.

Selam beyler! Denklemler tahtaya yazılır, dikkatlice bakın. Bu denklemlerin hepsini çözebilir misin? Hangileri değil ve neden?

Sol ve sağ tarafları kesirli rasyonel ifadeler olan denklemlere kesirli rasyonel denklemler denir. Bugün derste ne çalışacağımızı düşünüyorsun? Dersin konusunu formüle edin. Böylece defterleri açıp “Kesirli rasyonel denklemlerin çözümü” dersinin konusunu yazıyoruz.

2. Bilginin gerçekleşmesi. Ön anket, sınıfla sözlü çalışma.

Ve şimdi yeni bir konuyu incelemek için ihtiyaç duyduğumuz ana teorik materyali tekrarlayacağız. Lütfen gelecek soruları cevaplayın:

1. Denklem nedir? ( Değişken veya değişkenlerle eşitlik.)

2. Denklem #1'in adı nedir? ( Doğrusal.) Lineer denklemleri çözme yöntemi. ( Bilinmeyen her şeyi denklemin soluna, tüm sayıları sağa taşıyın. Gibi terimler getirin. Bilinmeyen çarpanı bulun).

3. Denklem #3'ün adı nedir? ( Meydan.) İkinci dereceden denklemleri çözme yöntemleri. ( Vieta teoremini ve sonuçlarını kullanarak formüllerle tam kare seçimi.)

4. Oran nedir? ( İki ilişkinin eşitliği.) Oranın ana özelliği. ( Oran doğruysa, uç terimlerinin çarpımı orta terimlerin çarpımına eşittir..)

5. Denklemlerin çözümünde hangi özellikler kullanılır? ( 1. Denklemde, işaretini değiştirerek terimi bir kısımdan diğerine aktarırsak, verilene eşdeğer bir denklem elde ederiz. 2. Denklemin her iki kısmı da sıfır olmayan aynı sayı ile çarpılır veya bölünürse, verilen denkleme eşdeğer bir denklem elde edilir..)

6. Kesir ne zaman sıfıra eşittir? ( Pay sıfır ve payda sıfır olmadığında kesir sıfırdır.)

3. Yeni malzemenin açıklaması.

Defterlerde ve tahtada 2 numaralı denklemi çözün.

Cevap: 10.

Oranın temel özelliğini kullanarak hangi kesirli rasyonel denklemi çözmeye çalışabilirsiniz? (Numara 5).

(x-2)(x-4) = (x+2)(x+3)

x2-4x-2x+8 = x2+3x+2x+6

x2-6x-x2-5x = 6-8

Defterlerde ve tahtada 4 numaralı denklemi çözün.

Cevap: 1,5.

Denklemin her iki tarafını payda ile çarparak hangi kesirli rasyonel denklemi çözmeyi deneyebilirsin? (No. 6).

D=1>0, x1=3, x2=4.

Cevap: 3;4.

Şimdi 7 numaralı denklemi yollardan biriyle çözmeye çalışın.

(x2-2x-5)x(x-5)=x(x-5)(x+5)
(x2-2x-5)x(x-5)-x(x-5)(x+5)=0
x(x-5)(x2-2x-5-(x+5))=0			x2-2x-5-x-5=0
x(x-5)(x2-3x-10)=0
x=0 x-5=0 x2-3x-10=0
x1=0 x2=5 D=49
Cevap: 0;5;-2.			Cevap: 5;-2.

Bunun neden olduğunu açıkla? Neden bir durumda üç, diğerinde iki kök var? Bu kesirli rasyonel denklemin kökleri hangi sayılardır?

Şimdiye kadar öğrenciler yabancı kök kavramıyla tanışmadılar, bunun neden olduğunu anlamak onlar için gerçekten çok zor. Sınıfta kimse bu duruma net bir açıklama getiremiyorsa öğretmen yönlendirici sorular sorar.

2 ve 4 numaralı denklemler 5,6,7 numaralı denklemlerden nasıl farklıdır? ( Sayının paydasındaki 2 ve 4 numaralı denklemlerde, No. 5-7 - değişkenli ifadeler.) Denklemin kökü nedir? ( Denklemin gerçek bir eşitlik haline geldiği değişkenin değeri.) Sayının denklemin kökü olup olmadığı nasıl anlaşılır? ( kontrol et.)

Bazı öğrenciler bir test yaparken sıfıra bölmek zorunda olduklarını fark ederler. 0 ve 5 sayılarının bu denklemin kökleri olmadığı sonucuna varıyorlar. Soru ortaya çıkıyor: Bu hatayı ortadan kaldıran kesirli rasyonel denklemleri çözmenin bir yolu var mı? Evet, bu yöntem kesrin sıfıra eşit olması şartına dayanmaktadır.

x2-3x-10=0, D=49, x1=5, x2=-2.

x=5 ise, x(x-5)=0, yani 5 yabancı bir köktür.

x=-2 ise, x(x-5)≠0.

Cevap: -2.

Kesirli rasyonel denklemleri bu şekilde çözmek için bir algoritma formüle etmeye çalışalım. Çocuklar algoritmayı kendileri formüle ederler.

Kesirli rasyonel denklemleri çözmek için algoritma:

1. Her şeyi sol tarafa taşıyın.

2. Kesirleri ortak bir paydaya getirin.

3. Bir sistem yapın: pay sıfıra eşit olduğunda kesir sıfıra eşittir ve payda sıfıra eşit değildir.

4. Denklemi çözün.

5. Yabancı kökleri hariç tutmak için eşitsizliği kontrol edin.

6. Cevabı yazın.

Tartışma: Temel orantı özelliği kullanılırsa çözümün nasıl formüle edileceği ve denklemin her iki tarafının ortak bir payda ile çarpılması. (Çözümü tamamlayın: ortak paydayı sıfıra çevirenleri köklerinden çıkarın).

4. Yeni materyalin birincil kavranması.

Çiftler halinde çalışın. Öğrenciler, denklemin türüne bağlı olarak denklemi nasıl çözeceklerini kendileri seçerler. "Cebir 8" ders kitabından görevler, 2007: No. 000 (b, c, i); 000(a, e, g). Öğretmen görevin performansını kontrol eder, ortaya çıkan soruları cevaplar ve düşük performans gösteren öğrencilere yardım sağlar. Kendi kendine test: Cevaplar tahtaya yazılır.

b) 2 yabancı bir köktür. Cevap:3.

c) 2 yabancı bir köktür. Cevap: 1.5.

a) Cevap: -12.5.

g) Cevap: 1; 1.5.

5. Ev ödevi beyanı.

2. Kesirli rasyonel denklemleri çözmek için algoritmayı öğrenin.

3. 000 (a, d, e) numaralı defterlerde çözün; 000(g, h).

4. No. 000(a)'yı (isteğe bağlı) çözmeye çalışın.

6. Çalışılan konuyla ilgili kontrol görevinin yerine getirilmesi.

İş levhalar üzerinde yapılır.

İş örneği:

A) Denklemlerden hangileri kesirli rasyoneldir?

B) Pay ________ ve payda __________ olduğunda bir kesir sıfırdır.

S) -3 sayısı Denklem #6'nın kökü müdür?

D) 7 numaralı denklemi çözün.

Görev değerlendirme kriterleri:

Öğrenci, görevin %90'ından fazlasını doğru bir şekilde tamamladıysa "5" verilir. Görevin %50'sinden azını tamamlayan öğrenciye "4" - %75 - %89 "3" - %50 - %74 "2" verilir. 2. sınıf dergiye yazılmaz, 3. sınıf isteğe bağlıdır.

7. Yansıma.

Bağımsız çalışmaya sahip broşürlere şunları koyun:

1 - ders sizin için ilginç ve anlaşılırsa; 2 - ilginç, ancak net değil; 3 - ilginç değil, anlaşılabilir; 4 - ilginç değil, net değil.

8. Dersi özetlemek.

Böylece, bugün derste kesirli rasyonel denklemlerle tanıştık, bu denklemleri çeşitli şekillerde nasıl çözeceğimizi öğrendik, bilgimizi eğitimden bağımsız çalışma yardımıyla test ettik. Bir sonraki derste bağımsız çalışmanın sonuçlarını öğreneceksiniz, evde edindiğiniz bilgileri pekiştirme fırsatına sahip olacaksınız.

Sizce kesirli rasyonel denklemleri çözmenin hangi yöntemi daha kolay, daha erişilebilir, daha rasyonel? Kesirli rasyonel denklemleri çözme yöntemi ne olursa olsun, unutulmaması gereken nedir? Kesirli rasyonel denklemlerin "kurnazlığı" nedir?

Hepinize teşekkürler, ders bitti.

Rasyonel ve kesirli rasyonel denklemleri tanıyalım, tanımlarını verelim, örnekler verelim ve ayrıca en yaygın problem türlerini analiz edelim.

Yandex.RTB R-A-339285-1

Rasyonel Denklem: Tanım ve Örnekler

Rasyonel ifadelerle tanışma, okulun 8. sınıfında başlar. Bu sıralarda cebir derslerinde öğrenciler, notlarında rasyonel ifadeler içeren denklemlerle giderek daha fazla görevle karşılaşmaya başlıyorlar. Ne olduğuna dair hafızamızı tazeleyelim.

tanım 1

rasyonel denklem her iki tarafı da rasyonel ifadeler içeren bir denklemdir.

Çeşitli kılavuzlarda başka bir ifade bulabilirsiniz.

tanım 2

rasyonel denklem- bu, sol tarafının kaydı rasyonel bir ifade içeren ve sağ tarafı sıfır içeren bir denklemdir.

Rasyonel denklemler için verdiğimiz tanımlar aynı anlama geldikleri için eşdeğerdir. Sözlerimizin doğruluğu, herhangi bir rasyonel ifade için P ve Q denklemler P=Q ve P - Q = 0 eşdeğer ifadeler olacaktır.

Şimdi örneklere dönelim.

örnek 1

Rasyonel denklemler:

x = 1 , 2 x − 12 x 2 y z 3 = 0 , x x 2 + 3 x - 1 = 2 + 2 7 x - a (x + 2) , 1 2 + 3 4 - 12 x - 1 = 3 .

Rasyonel denklemler, tıpkı diğer türdeki denklemler gibi, 1'den birkaça kadar herhangi bir sayıda değişken içerebilir. Başlangıç ​​olarak, denklemlerin sadece bir değişken içereceği basit örneklere bakacağız. Ve sonra görevi yavaş yavaş karmaşıklaştırmaya başlıyoruz.

Rasyonel denklemler iki büyük gruba ayrılır: tamsayı ve kesirli. Bakalım her bir grup için hangi denklemler geçerli olacak.

tanım 3

Sol ve sağ bölümlerinin kaydı tüm rasyonel ifadeleri içeriyorsa, rasyonel bir denklem bir tamsayı olacaktır.

Tanım 4

Parçalarından biri veya her ikisi de bir kesir içeriyorsa, rasyonel bir denklem kesirli olacaktır.

Kesirli rasyonel denklemler mutlaka bir değişkenle bölme içerir veya değişken paydada bulunur. Tamsayılı denklemlerin yazılmasında böyle bir bölünme yoktur.

Örnek 2

3 x + 2 = 0 ve (x + y) (3 x 2 − 1) + x = − y + 0 , 5 tam rasyonel denklemlerdir. Burada denklemin her iki kısmı da tamsayı ifadeleriyle temsil edilir.

1 x - 1 = x 3 ve x: (5 x 3 + y 2) = 3: (x − 1) : 5 kesirli rasyonel denklemlerdir.

Tüm rasyonel denklemler, doğrusal ve ikinci dereceden denklemleri içerir.

Tüm denklemleri çözme

Bu tür denklemlerin çözümü genellikle bunların eşdeğer cebirsel denklemlere dönüştürülmesine indirgenir. Bu, aşağıdaki algoritmaya göre denklemlerin eşdeğer dönüşümlerini gerçekleştirerek başarılabilir:

• ilk önce denklemin sağ tarafında sıfır alırız, bunun için denklemin sağ tarafında bulunan ifadeyi soluna aktarıp işaretini değiştirmek gerekir;
• sonra denklemin sol tarafındaki ifadeyi standart form polinomuna dönüştürüyoruz.

Cebirsel bir denklem bulmalıyız. Bu denklem, orijinal denkleme göre eşdeğer olacaktır. Kolay durumlar, tüm denklemi doğrusal veya ikinci dereceden bir denkleme indirgeyerek sorunu çözmemize izin verir. Genel durumda, cebirsel bir derece denklemini çözeriz. n.

Örnek 3

Tüm denklemin köklerini bulmak gerekir 3 (x + 1) (x − 3) = x (2 x − 1) − 3.

Çözüm

Eşdeğer bir cebirsel denklem elde etmek için orijinal ifadeyi dönüştürelim. Bunu yapmak için denklemin sağ tarafında yer alan ifadeyi sol tarafa aktaracağız ve işareti ters çevireceğiz. Sonuç olarak şunları elde ederiz: 3 (x + 1) (x − 3) − x (2 x − 1) + 3 = 0.

Şimdi sol taraftaki ifadeyi standart formun bir polinomuna çevireceğiz ve bu polinom ile gerekli işlemleri yapacağız:

3 (x + 1) (x - 3) - x (2 x - 1) + 3 = (3 x + 3) (x - 3) - 2 x 2 + x + 3 = = 3 x 2 - 9 x + 3 x - 9 - 2 x 2 + x + 3 = x 2 - 5 x - 6

Orijinal denklemin çözümünü, formun ikinci dereceden bir denkleminin çözümüne indirmeyi başardık. x 2 − 5 x − 6 = 0. Bu denklemin diskriminantı pozitiftir: D = (− 5) 2 − 4 1 (− 6) = 25 + 24 = 49 . Bu, iki gerçek kök olacağı anlamına gelir. Onları ikinci dereceden denklemin köklerinin formülünü kullanarak bulalım:

x \u003d - - 5 ± 49 2 1,

x 1 \u003d 5 + 7 2 veya x 2 \u003d 5 - 7 2,

x 1 = 6 veya x 2 = - 1

Çözüm sürecinde bulduğumuz denklemin köklerinin doğruluğunu kontrol edelim. Aldığımız bu sayı için orijinal denklemi yerine koyarız: 3 (6 + 1) (6 − 3) = 6 (2 6 − 1) − 3 ve 3 (− 1 + 1) (− 1 − 3) = (− 1) (2 (− 1) − 1) − 3. İlk durumda 63 = 63 , saniyede 0 = 0 . kökler x=6 ve x = − 1 gerçekten de örnek durumda verilen denklemin kökleridir.

Cevap: 6 , − 1 .

"Bütün denklemin gücü" ne anlama geliyor ona bakalım. Bu terimle, tüm bir denklemi cebirsel bir biçimde temsil etmemiz gereken durumlarda sıklıkla karşılaşacağız. Konsepti tanımlayalım.

tanım 5

Bir tamsayı denkleminin derecesi orijinal bütün denkleme eşdeğer bir cebirsel denklemin derecesidir.

Yukarıdaki örnekteki denklemlere bakarsanız, şunları kurabilirsiniz: tüm bu denklemin derecesi ikincidir.

Kursumuz ikinci dereceden denklemleri çözmekle sınırlı olsaydı, konunun değerlendirilmesi burada tamamlanabilirdi. Ama her şey o kadar basit değil. Üçüncü dereceden denklemleri çözmek zorluklarla doludur. Ve dördüncü derecenin üzerindeki denklemler için kökler için hiçbir genel formül yoktur. Bu bağlamda, üçüncü, dördüncü ve diğer derecelerin tüm denklemlerinin çözümü, bir dizi başka teknik ve yöntem kullanmamızı gerektirir.

Tüm rasyonel denklemleri çözmek için en yaygın olarak kullanılan yaklaşım, çarpanlara ayırma yöntemine dayanmaktadır. Bu durumda eylemlerin algoritması aşağıdaki gibidir:

• ifadeyi sağdan sola aktarırız, böylece kaydın sağ tarafında sıfır kalır;
• sol taraftaki ifadeyi faktörlerin bir ürünü olarak temsil ediyoruz ve sonra bir dizi daha basit denkleme geçiyoruz.

Örnek 4

(x 2 − 1) (x 2 − 10 x + 13) = 2 x (x 2 − 10 x + 13) denkleminin çözümünü bulun.

Çözüm

İfadeyi kaydın sağ tarafından zıt işaretli sol tarafa aktarıyoruz: (x 2 − 1) (x 2 − 10 x + 13) − 2 x (x 2 − 10 x + 13) = 0. Sol tarafı standart formun bir polinomuna dönüştürmek, bunun bize dördüncü dereceden bir cebirsel denklem vereceği gerçeğinden dolayı pratik değildir: x 4 − 12 x 3 + 32 x 2 − 16 x − 13 = 0. Dönüşümün kolaylığı, böyle bir denklemi çözmenin tüm zorluklarını haklı çıkarmaz.

Diğer yoldan gitmek çok daha kolay: ortak faktörü çıkarıyoruz x 2 − 10 x + 13 . Böylece formun bir denklemine ulaşırız (x 2 − 10 x + 13) (x 2 − 2 x − 1) = 0. Şimdi ortaya çıkan denklemi bir dizi iki ikinci dereceden denklemle değiştiriyoruz. x 2 − 10 x + 13 = 0 ve x 2 − 2 x − 1 = 0 ve ayrımcı aracılığıyla köklerini bulun: 5 + 2 3 , 5 - 2 3 , 1 + 2 , 1 - 2 .

Cevap: 5 + 2 3 , 5 - 2 3 , 1 + 2 , 1 - 2 .

Benzer şekilde, yeni bir değişken tanıtma yöntemini kullanabiliriz. Bu yöntem, orijinal tam denklemdekinden daha düşük güçlere sahip eşdeğer denklemlere geçmemizi sağlar.

Örnek 5

Denklemin kökleri var mı? (x 2 + 3 x + 1) 2 + 10 = − 2 (x 2 + 3 x − 4)?

Çözüm

Şimdi bütün bir rasyonel denklemi cebirsel bir denkleme indirgemeye çalışırsak, rasyonel kökleri olmayan 4. dereceden bir denklem elde ederiz. Bu nedenle, diğer yoldan gitmemiz daha kolay olacaktır: denklemdeki ifadenin yerini alacak yeni bir y değişkeni tanıtın. x 2 + 3 x.

Şimdi tüm denklemle çalışacağız (y + 1) 2 + 10 = − 2 (y − 4). Denklemin sağ tarafını zıt işaretli sol tarafa aktarıyoruz ve gerekli dönüşümleri yapıyoruz. Alırız: y 2 + 4 y + 3 = 0. İkinci dereceden denklemin köklerini bulalım: y = − 1 ve y = - 3.

Şimdi ters ikame yapalım. iki denklem elde ederiz x 2 + 3 x = − 1 ve x 2 + 3 x = - 3 . Bunları x 2 + 3 x + 1 = 0 olarak yeniden yazalım ve x 2 + 3 x + 3 = 0. Elde edilen ilk denklemin köklerini bulmak için ikinci dereceden denklemin köklerinin formülünü kullanırız: - 3 ± 5 2 . İkinci denklemin diskriminantı negatiftir. Bu, ikinci denklemin gerçek köklerinin olmadığı anlamına gelir.

Cevap:- 3 ± 5 2

Yüksek dereceli tamsayılı denklemler problemlerde oldukça sık karşımıza çıkar. Onlardan korkmaya gerek yok. Bir dizi yapay dönüşüm de dahil olmak üzere, bunları çözmek için standart olmayan bir yöntem uygulamaya hazır olmanız gerekir.

Kesirli rasyonel denklemlerin çözümü

Bu alt konuyu değerlendirmemize, p (x) q (x) = 0 biçimindeki kesirli rasyonel denklemleri çözmek için bir algoritma ile başlıyoruz. p(x) ve q(x) tamsayı rasyonel ifadelerdir. Diğer kesirli rasyonel denklemlerin çözümü, her zaman belirtilen formdaki denklemlerin çözümüne indirgenebilir.

p (x) q (x) = 0 denklemlerini çözmek için en sık kullanılan yöntem aşağıdaki ifadeye dayanmaktadır: sayısal kesir sen v, nerede v sıfırdan farklı, yalnızca kesrin payının sıfıra eşit olduğu durumlarda sıfıra eşit olan bir sayıdır. Yukarıdaki ifadenin mantığını izleyerek, p (x) q (x) = 0 denkleminin çözümünün iki koşulun sağlanmasına indirgenebileceğini söyleyebiliriz: p(x)=0 ve q(x) ≠ 0. Bunun üzerine, p (x) q (x) = 0 biçimindeki kesirli rasyonel denklemleri çözmek için bir algoritma oluşturulmuştur:

• tüm rasyonel denklemin çözümünü buluruz p(x)=0;
• Çözüm sırasında bulunan kökler için koşulun sağlanıp sağlanmadığını kontrol ederiz. q(x) ≠ 0.

Bu koşul sağlanırsa kök bulunur, değilse kök soruna çözüm değildir.

Örnek 6

3 · x - 2 5 · x 2 - 2 = 0 denkleminin köklerini bulun.

Çözüm

p (x) q (x) = 0 biçiminde, p (x) = 3 · x − 2 , q (x) = 5 · x 2 − 2 = 0 olan kesirli rasyonel bir denklemle uğraşıyoruz. Lineer denklemi çözmeye başlayalım 3x - 2 = 0. Bu denklemin kökü x = 2 3.

Bulunan kökü kontrol edelim, koşulu sağlayıp sağlamadığını 5 x 2 - 2 ≠ 0. Bunu yapmak için, ifadeye sayısal bir değer koyun. Alırız: 5 2 3 2 - 2 \u003d 5 4 9 - 2 \u003d 20 9 - 2 \u003d 2 9 ≠ 0.

Koşul karşılandı. Demek oluyor x = 2 3 orijinal denklemin köküdür.

Cevap: 2 3 .

p (x) q (x) = 0 kesirli rasyonel denklemleri çözmek için başka bir seçenek var. Bu denklemin tüm denkleme eşdeğer olduğunu hatırlayın. p(x)=0 orijinal denklemin x değişkeninin kabul edilebilir değerleri aralığında. Bu, p(x) q(x) = 0 denklemlerinin çözümünde aşağıdaki algoritmayı kullanmamıza izin verir:

• denklemi çözün p(x)=0;
• x değişkeni için kabul edilebilir değer aralığını bulun;
• x değişkeninin kabul edilebilir değerleri bölgesinde bulunan kökleri orijinal kesirli rasyonel denklemin istenen kökleri olarak alıyoruz.

Örnek 7

x 2 - 2 x - 11 x 2 + 3 x = 0 denklemini çözün.

Çözüm

Önce ikinci dereceden denklemi çözelim x 2 − 2 x − 11 = 0. Köklerini hesaplamak için, ikinci bir katsayı için kök formülünü kullanırız. alırız D 1 = (− 1) 2 − 1 (− 11) = 12 ve x = 1 ± 2 3 .

Şimdi orijinal denklem için x'in ODV'sini bulabiliriz. Bunların hepsi hangi sayılar x 2 + 3 x ≠ 0. Aynı x (x + 3) ≠ 0, nereden x ≠ 0 , x ≠ − 3 .

Şimdi çözümün ilk aşamasında elde edilen x = 1 ± 2 3 köklerinin x değişkeninin kabul edilebilir değerleri aralığında olup olmadığını kontrol edelim. Neyin girdiğini görüyoruz. Bu, orijinal kesirli rasyonel denklemin iki kökü x = 1 ± 2 3 olduğu anlamına gelir.

Cevap: x = 1 ± 2 3

Tanımlanan ikinci çözüm yöntemi, x değişkeninin kabul edilebilir değerlerinin alanının kolayca bulunduğu ve denklemin köklerinin bulunduğu durumlarda birinciden daha basittir. p(x)=0 mantıksız. Örneğin, 7 ± 4 26 9 . Kökler rasyonel olabilir, ancak büyük bir pay veya payda ile. Örneğin, 127 1101 ve − 31 59 . Bu, durumu kontrol etmek için zaman kazandırır. q(x) ≠ 0: ODZ'ye göre uymayan kökleri dışlamak çok daha kolaydır.

Denklemin kökleri ne zaman p(x)=0 tamsayılarsa, p (x) q (x) = 0 biçimindeki denklemleri çözmek için açıklanan algoritmalardan ilkini kullanmak daha uygundur. Tüm denklemin köklerini daha hızlı bulma p(x)=0 ve ardından koşulun onlar için karşılanıp karşılanmadığını kontrol edin q(x) ≠ 0 ve ODZ'yi bulmayın ve ardından denklemi çözün p(x)=0 bu ODZ'de. Bunun nedeni, bu gibi durumlarda kontrol yapmanın genellikle ODZ'yi bulmaktan daha kolay olmasıdır.

Örnek 8

Denklemin köklerini bulun (2 x - 1) (x - 6) (x 2 - 5 x + 14) (x + 1) x 5 - 15 x 4 + 57 x 3 - 13 x 2 + 26 x + 112 = 0 .

Çözüm

Tüm denklemi göz önünde bulundurarak başlıyoruz (2 x - 1) (x - 6) (x 2 - 5 x + 14) (x + 1) = 0 ve köklerini bulmak. Bunu yapmak için, çarpanlara ayırma yoluyla denklem çözme yöntemini uygularız. Orijinal denklemin 2 x - 1 = 0, x - 6 = 0, x 2 - 5 x + 14 = 0, x + 1 = 0, üçü doğrusal ve biri kare. Kökleri buluyoruz: ilk denklemden x = 1 2, ikinciden x=6, üçüncüden - x \u003d 7, x \u003d - 2, dördüncüden - x = − 1.

Elde edilen kökleri kontrol edelim. Bu durumda ODZ'yi belirlemek bizim için zor, çünkü bunun için beşinci dereceden bir cebirsel denklemi çözmemiz gerekecek. Denklemin sol tarafında yer alan kesrin paydasının kaybolmaması durumunu kontrol etmek daha kolay olacaktır.

Sırayla, ifadedeki x değişkeninin yerine kökleri değiştirin. x 5 − 15 x 4 + 57 x 3 − 13 x 2 + 26 x + 112 ve değerini hesaplayın:

1 2 5 - 15 1 2 4 + 57 1 2 3 - 13 1 2 2 + 26 1 2 + 112 = = 1 32 - 15 16 + 57 8 - 13 4 + 13 + 112 = 122 + 1 32 ≠0;

6 5 − 15 6 4 + 57 6 3 − 13 6 2 + 26 6 + 112 = 448 ≠ 0;

7 5 − 15 7 4 + 57 7 3 − 13 7 2 + 26 7 + 112 = 0;

(− 2) 5 − 15 (− 2) 4 + 57 (− 2) 3 − 13 (− 2) 2 + 26 (− 2) + 112 = − 720 ≠ 0 ;

(− 1) 5 − 15 (− 1) 4 + 57 (− 1) 3 − 13 (− 1) 2 + 26 (− 1) + 112 = 0 .

Gerçekleştirilen doğrulama, orijinal kesirli rasyonel denklemin köklerinin 1 2 , 6 ve − 2 .

Cevap: 1 2 , 6 , - 2

Örnek 9

5 x 2 - 7 x - 1 x - 2 x 2 + 5 x - 14 = 0 kesirli rasyonel denklemin köklerini bulun.

Çözüm

denklemle başlayalım (5 x 2 - 7 x - 1) (x - 2) = 0. Köklerini bulalım. Bu denklemi ikinci dereceden ve doğrusal denklemlerin bir kombinasyonu olarak temsil etmek bizim için daha kolaydır. 5 x 2 - 7 x - 1 = 0 ve x − 2 = 0.

Kökleri bulmak için ikinci dereceden bir denklemin köklerinin formülünü kullanırız. Birinci denklemden x = 7 ± 69 10 ve ikincisinden iki kök elde ederiz. x=2.

Koşulları kontrol etmek için köklerin değerini orijinal denklemde yerine koymak bizim için oldukça zor olacaktır. x değişkeninin LPV'sini belirlemek daha kolay olacaktır. Bu durumda, x değişkeninin DPV'si, koşulun sağlandığı sayılar dışında tüm sayılardır. x 2 + 5 x − 14 = 0. Şunları elde ederiz: x ∈ - ∞ , - 7 ∪ - 7 , 2 ∪ 2 , + ∞ .

Şimdi bulduğumuz köklerin x değişkeni için kabul edilebilir değerler aralığına ait olup olmadığını kontrol edelim.

x = 7 ± 69 10 - kökleri aittir, bu nedenle, bunlar orijinal denklemin kökleridir ve x=2- ait değildir, bu nedenle yabancı bir köktür.

Cevap: x = 7 ± 69 10 .

p (x) q (x) = 0 biçimindeki kesirli rasyonel bir denklemin payının bir sayı içerdiği durumları ayrı ayrı inceleyelim. Bu gibi durumlarda, pay sıfırdan farklı bir sayı içeriyorsa, denklemin kökleri olmayacaktır. Bu sayı sıfıra eşitse, denklemin kökü ODZ'den herhangi bir sayı olacaktır.

Örnek 10

Kesirli rasyonel denklemi çözün - 3 , 2 x 3 + 27 = 0.

Çözüm

Bu denklemin kökleri olmayacak, çünkü denklemin sol tarafındaki kesrin payı sıfır olmayan bir sayı içeriyor. Bu, herhangi bir x değeri için, problem durumunda verilen kesrin değerinin sıfıra eşit olmayacağı anlamına gelir.

Cevap: kök yok.

Örnek 11

0 x 4 + 5 x 3 = 0 denklemini çözün.

Çözüm

Kesrin payı sıfır olduğundan, denklemin çözümü ODZ değişkeninden x'in herhangi bir değeri olacaktır.

Şimdi ODZ'yi tanımlayalım. Bunun için tüm x değerlerini içerecektir. x 4 + 5 x 3 ≠ 0. denklem çözümleri x 4 + 5 x 3 = 0 vardır 0 ve − 5 , bu denklem denkleme eşdeğer olduğundan x 3 (x + 5) = 0, ve sırayla, iki denklem kümesine eşdeğerdir x 3 = 0 ve x + 5 = 0 bu köklerin göründüğü yer. İstenen kabul edilebilir değer aralığının herhangi bir x olduğu sonucuna varıyoruz. x=0 ve x = -5.

0 x 4 + 5 x 3 = 0 kesirli rasyonel denkleminin, sıfır ve - 5 dışında herhangi bir sayı olan sonsuz sayıda çözümü olduğu ortaya çıktı.

Cevap: - ∞ , - 5 ∪ (- 5 , 0 ∪ 0 , + ∞

Şimdi keyfi bir formun kesirli rasyonel denklemleri ve bunları çözme yöntemleri hakkında konuşalım. olarak yazılabilirler r(x) = s(x), nerede r(x) ve s(x) rasyonel ifadelerdir ve bunlardan en az biri kesirlidir. Bu tür denklemlerin çözümü, p (x) q (x) = 0 biçimindeki denklemlerin çözümüne indirgenir.

Denklemin sağ tarafındaki ifadeyi zıt işaretli sol tarafa aktararak eşdeğer bir denklem elde edebileceğimizi zaten biliyoruz. Bu, denklemin r(x) = s(x) denkleme eşdeğerdir r (x) - s (x) = 0. Rasyonel bir ifadenin rasyonel bir kesre nasıl dönüştürüleceğini de zaten tartıştık. Bu sayede denklemi kolayca dönüştürebiliriz. r (x) - s (x) = 0 p (x) q (x) formunun özdeş rasyonel fraksiyonuna .

Bu yüzden orijinal kesirli rasyonel denklemden hareket ediyoruz r(x) = s(x) nasıl çözüleceğini öğrendiğimiz p (x) q (x) = 0 biçimindeki bir denkleme.

Unutulmamalıdır ki, geçişler yapılırken r (x) - s (x) = 0 p (x) q (x) = 0'a ve sonra p(x)=0 x değişkeninin geçerli değer aralığının genişlemesini dikkate almayabiliriz.

Orijinal denklemin oldukça gerçekçi r(x) = s(x) ve denklem p(x)=0 dönüşümlerin bir sonucu olarak, eşdeğer olmaktan çıkacaktır. O halde denklemin çözümü p(x)=0 bize yabancı olacak kökler verebilir r(x) = s(x). Bu bağlamda, her durumda, yukarıda açıklanan yöntemlerden herhangi biri ile bir kontrol yapılması gerekir.

Konuyu incelemenizi kolaylaştırmak için, formun kesirli rasyonel bir denklemini çözmek için tüm bilgileri bir algoritmaya genelleştirdik. r(x) = s(x):

• ifadeyi sağ taraftan zıt işaretle aktarır ve sağda sıfır alırız;
• kesirler ve polinomlarla sırayla eylemler gerçekleştirerek orijinal ifadeyi rasyonel bir p (x) q (x) kesrine dönüştürürüz;
• denklemi çözün p(x)=0;
• ODZ'ye ait olduklarını kontrol ederek veya orijinal denklemde yerine koyarak yabancı kökleri ortaya çıkarırız.

Görsel olarak, eylem zinciri şöyle görünecektir:

r (x) = s (x) → r (x) - s (x) = 0 → p (x) q (x) = 0 → p (x) = 0 → bırakma r o n d e r o o n s

Örnek 12

Kesirli rasyonel denklemi x x + 1 = 1 x + 1 çözün.

Çözüm

Şimdi x x + 1 - 1 x + 1 = 0 denklemine geçelim. Denklemin sol tarafındaki kesirli rasyonel ifadeyi p (x) q (x) formuna dönüştürelim.

Bunu yapmak için, rasyonel kesirleri ortak bir paydaya indirgemeli ve ifadeyi sadeleştirmeliyiz:

x x + 1 - 1 x - 1 = x x - 1 (x + 1) - 1 x (x + 1) x (x + 1) = = x 2 - x - 1 - x 2 - x x (x + 1) = - 2 x - 1 x (x + 1)

- 2 x - 1 x (x + 1) = 0 denkleminin köklerini bulmak için denklemi çözmemiz gerekir. − 2 x − 1 = 0. Bir kök alıyoruz x = - 1 2.

Herhangi bir yöntemle kontrolü gerçekleştirmek bize kalır. İkisini de düşünelim.

Ortaya çıkan değeri orijinal denklemde değiştirin. - 1 2 - 1 2 + 1 = 1 - 1 2 + 1 elde ederiz. Doğru sayısal eşitliğe geldik − 1 = − 1 . Demek oluyor x = − 1 2 orijinal denklemin köküdür.

Şimdi ODZ'yi kontrol edeceğiz. x değişkeni için kabul edilebilir değerlerin alanını belirleyelim. Bu, − 1 ve 0 hariç tüm sayı kümesi olacaktır (x = − 1 ve x = 0 olduğunda, kesirlerin paydaları kaybolur). aldığımız kök x = − 1 2 ODZ'ye aittir. Bu, orijinal denklemin kökü olduğu anlamına gelir.

Cevap: − 1 2 .

Örnek 13

x 1 x + 3 - 1 x = - 2 3 x denkleminin köklerini bulun.

Çözüm

Kesirli rasyonel bir denklemle uğraşıyoruz. Bu nedenle algoritmaya göre hareket edeceğiz.

İfadeyi sağdan sola, zıt işaretli olarak taşıyalım: x 1 x + 3 - 1 x + 2 3 x = 0

Gerekli dönüşümleri yapalım: x 1 x + 3 - 1 x + 2 3 x = x 3 + 2 x 3 = 3 x 3 = x.

denkleme geliyoruz x=0. Bu denklemin kökü sıfırdır.

Bu kökün orijinal denklem için yabancı olup olmadığını kontrol edelim. Orijinal denklemdeki değeri değiştirin: 0 1 0 + 3 - 1 0 = - 2 3 0 . Gördüğünüz gibi, ortaya çıkan denklem mantıklı değil. Bu, 0'ın yabancı bir kök olduğu ve orijinal kesirli rasyonel denklemin kökü olmadığı anlamına gelir.

Cevap: kök yok.

Algoritmaya diğer eşdeğer dönüşümleri dahil etmediysek, bu onların kullanılamayacağı anlamına gelmez. Algoritma evrenseldir, ancak sınırlamak için değil, yardımcı olmak için tasarlanmıştır.

Örnek 14

7 + 1 3 + 1 2 + 1 5 - x 2 = 7 7 24 denklemini çözün

Çözüm

En kolay yol, verilen kesirli rasyonel denklemi algoritmaya göre çözmektir. Ama başka bir yol var. Düşünelim.

Sağ ve sol kısımlardan 7 çıkarın, şunu elde ederiz: 1 3 + 1 2 + 1 5 - x 2 \u003d 7 24.

Bundan, sol tarafın paydasındaki ifadenin, sağ taraftaki sayının tersi olan sayıya eşit olması gerektiği sonucuna varabiliriz, yani 3 + 1 2 + 1 5 - x 2 = 24 7 .

Her iki kısımdan da çıkarın 3: 1 2 + 1 5 - x 2 = 3 7 . Analojiyle 2 + 1 5 - x 2 \u003d 7 3, buradan 1 5 - x 2 \u003d 1 3 ve ayrıca 5 - x 2 \u003d 3, x 2 \u003d 2, x \u003d ± 2

Bulunan köklerin orijinal denklemin kökleri olup olmadığını belirlemek için kontrol edelim.

Cevap: x = ± 2

Metinde bir hata fark ederseniz, lütfen vurgulayın ve Ctrl+Enter tuşlarına basın.

Şimdiye kadar sadece bilinmeyene göre tamsayılı denklemleri, yani paydalarının (varsa) bilinmeyeni içermediği denklemleri çözdük.

Genellikle paydalarında bilinmeyeni içeren denklemleri çözmeniz gerekir: bu tür denklemlere kesirli denir.

Bu denklemi çözmek için, her iki tarafı da bilinmeyeni içeren bir polinomla çarpıyoruz. Yeni denklem verilene eşdeğer olacak mı? Soruyu cevaplamak için, bu denklemi çözelim.

Her iki tarafını da ile çarparsak, şunu elde ederiz:

Birinci dereceden bu denklemi çözerek şunları buluruz:

Yani, denklem (2) tek bir köke sahiptir

Bunu denklem (1) ile değiştirerek şunu elde ederiz:

Dolayısıyla, aynı zamanda (1) denkleminin köküdür.

Denklem (1)'in başka kökü yoktur. Örneğimizde bu, örneğin (1) denklemindeki gerçeğinden görülebilir.

Bilinmeyen bölen, bölüm 2'ye bölünen temettü 1'e nasıl eşit olmalıdır, yani.

Dolayısıyla (1) ve (2) denklemlerinin tek bir kökü vardır ve bu nedenle eşdeğerdirler.

2. Şimdi aşağıdaki denklemi çözüyoruz:

En basit ortak payda: ; denklemin tüm terimlerini bununla çarpın:

İndirgemeden sonra şunu elde ederiz:

Parantezleri genişletelim:

Benzer terimler getirerek, elimizde:

Bu denklemi çözerek şunları buluruz:

(1) denklemini değiştirerek şunu elde ederiz:

Sol tarafta ise bir anlam ifade etmeyen ifadeler aldık.

Bu nedenle, (1) denkleminin kökü değildir. Bu, (1) denklemlerinin eşdeğer olmadığı anlamına gelir.

Bu durumda, (1) denkleminin yabancı bir kök aldığını söylüyoruz.

(1) denkleminin çözümünü daha önce ele aldığımız denklemlerin çözümüyle karşılaştıralım (bkz. § 51). Bu denklemi çözerken, daha önce karşılaşılmamış iki işlem yapmak zorundaydık: ilk olarak, denklemin her iki tarafını bilinmeyen (ortak payda) içeren bir ifadeyle çarpmıştık ve ikincisi, cebirsel kesirleri aşağıdakileri içeren çarpanlara indirgedik. bir bilinmeyen.

Denklem (1) ile Denklem (2)'yi karşılaştırdığımızda, Denklem (2) için geçerli olan tüm x değerlerinin Denklem (1) için geçerli olmadığını görüyoruz.

(1) denklemi için bilinmeyenin kabul edilebilir değerleri olmayan 1 ve 3 sayılarıdır ve dönüşüm sonucunda denklem (2) için kabul edilebilir hale gelmiştir. Bu sayılardan biri (2) numaralı denklemin çözümü olarak ortaya çıktı, ancak elbette (1) numaralı denklemin çözümü olamaz. Denklem (1)'in çözümü yoktur.

Bu örnek, denklemin her iki parçasını bilinmeyeni içeren bir faktörle çarparken ve cebirsel kesirleri azaltırken, verilene eşdeğer olmayan bir denklemin elde edilebileceğini gösterir, yani: yabancı kökler görünebilir.

Bu nedenle, aşağıdaki sonucu çıkarıyoruz. Paydasında bilinmeyen içeren bir denklemi çözerken, elde edilen kökler orijinal denkleme ikame edilerek kontrol edilmelidir. Yabancı kökler atılmalıdır.

"Polinomlu rasyonel denklemler" matematikte USE testlerinde en sık karşılaşılan konulardan biridir. Bu nedenle tekrarlarına özellikle dikkat edilmelidir. Birçok öğrenci, diskriminant bulma, göstergeleri sağdan sola aktarma ve denklemi ortak bir paydaya getirme sorunu ile karşı karşıya kalmaktadır ve bu da bu tür görevleri tamamlamayı zorlaştırmaktadır. Web sitemizdeki sınava hazırlanırken rasyonel denklemleri çözmek, herhangi bir karmaşıklıktaki görevlerle hızlı bir şekilde başa çıkmanıza ve testi mükemmel bir şekilde geçmenize yardımcı olacaktır.

Matematikte birleşik sınava başarılı bir şekilde hazırlanmak için eğitim portalı "Shkolkovo"yu seçin!

Bilinmeyenleri hesaplama kurallarını bilmek ve doğru sonuçları kolayca almak için çevrimiçi hizmetimizi kullanın. Shkolkovo portalı, sınava hazırlanmak için gerekli malzemelerin toplandığı türünün tek örneği bir platformdur. Öğretmenlerimiz tüm matematik kurallarını sistematize ederek anlaşılır bir şekilde sunmuştur. Ek olarak, okul çocuklarını, temeli sürekli güncellenen ve tamamlanan tipik rasyonel denklemleri çözmede ellerini denemeye davet ediyoruz.

Teste daha etkili bir hazırlık için, özel yöntemimizi izlemenizi ve kuralları tekrarlayarak ve basit problemleri çözerek başlamanızı, yavaş yavaş daha karmaşık olanlara geçmenizi öneririz. Böylece mezun, kendisi için en zor konuları vurgulayabilecek ve çalışmalarına odaklanabilecektir.

Bugün Shkolkovo ile son test için hazırlanmaya başlayın ve sonuç sizi bekletmeyecek! Verilenlerden en kolay örneği seçin. İfadede hızlı bir şekilde ustalaştıysanız, daha zor bir göreve geçin. Böylece bilginizi profil düzeyinde matematikte USE görevlerini çözecek kadar geliştirebilirsiniz.

Eğitim sadece Moskova'dan mezunlar için değil, aynı zamanda diğer şehirlerden gelen okul çocukları için de mevcuttur. Örneğin, portalımızda günde birkaç saat çalışarak geçirin ve çok yakında herhangi bir karmaşıklıktaki denklemlerle başa çıkabileceksiniz!