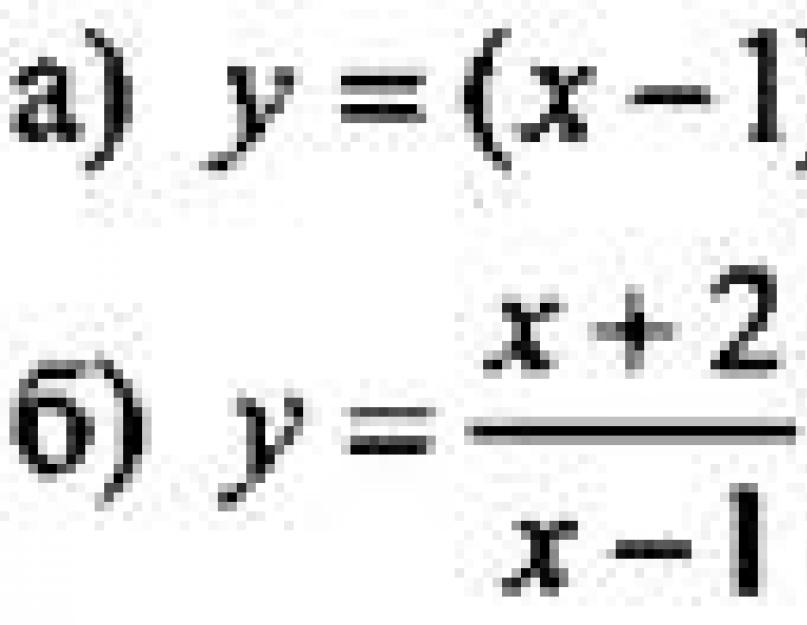5. Ders

Hedef: modüllerle grafikleri dönüştürmenin temel becerilerine hakim olun.

I. Konunun ve dersin amacının iletilmesi

II . Kapsanan malzemenin tekrarı ve konsolidasyonu

1. Soruların yanıtları ev ödevi(çözülmemiş sorunların analizi).

2. Materyalin asimilasyonunun izlenmesi (yazılı anket).

seçenek 1

f (x), y = fonksiyonunu çizin f(-x) + 2?

2. Fonksiyonu çizin:

seçenek 2

1. Nasıl, y = fonksiyonunun grafiğini bilmek f (x), y = - fonksiyonunu çizin f(x) - 1?

2. Fonksiyonu çizin:

III. Yeni materyal öğrenmek

Önceki dersin materyalinden, grafikleri dönüştürme yöntemlerinin yapımında son derece yararlı olduğu görülebilir. Bu nedenle, modülleri içeren grafikleri dönüştürmek için ana yöntemleri de ele alacağız. Bu yöntemler evrenseldir ve herhangi bir işlev için uygundur. İnşaatın basitliği için parçalı lineer bir fonksiyonu ele alacağız. f (x) kapsam ile D(f ), grafiği şekilde gösterilmiştir. Modüllü grafiklerin üç standart dönüşümünü ele alalım.

1) y = | fonksiyonunun çizimi f(x)|

f /(x), eğer Dx)>0,

Modülün tanımına göre şunları elde ederiz:Bu, y = | fonksiyonunun çizilmesi anlamına gelir. f(x )| y \u003d fonksiyonunun grafiğinin bir bölümünü kaydetmek gerekir f(x ), bunun için y ≥ 0. y = fonksiyonunun grafiğinin bu kısmı f (x) hangi y için< 0, надо симметрично отразить вверх относительно оси абсцисс.

2) y = fonksiyonunun çizimi f(|x|)

G / O), eğer Dx)> 0 ise,

Modülü genişletin ve şunları elde edin:Bu nedenle, y = fonksiyonunu çizmek için f(|x |) y = fonksiyonunun grafiğinin bir kısmını kaydetmek gerekir f (x), bunun için x ≥ 0. Ek olarak, bu kısım y eksenine göre simetrik olarak sola yansıtılmalıdır.

3) Denklem |y| = f(x)

Modülün tanımı gereği, buna sahibiz f (x) ≥ 0 iki fonksiyonun grafiklerini oluşturmak gereklidir: y = f(x) ve y=-f (X). Bu, |y| denklemini çizmek anlamına gelir. = f (x) y \u003d fonksiyonunun grafiğinin bir bölümünü kaydetmek gerekir f (x), bunun için y ≥ 0. Ek olarak, bu kısım x eksenine göre simetrik olarak aşağı yansıtılmalıdır.

|y| = f (x) bir fonksiyon tanımlamaz, yani x için∈ (-2.6; 1.4) her x değeri iki y değerine karşılık gelir. Bu nedenle, şekil tam olarak |у| denkleminin grafiğini göstermektedir. = f(x).

Daha fazlasını çizmek için grafikleri modüllerle dönüştürmek için dikkate alınan yöntemleri kullanıyoruz. karmaşık fonksiyonlar ve denklemler.

örnek 1

fonksiyonu çizelim

Bu fonksiyonda tamsayı kısmını seçiyoruzBöyle bir grafik, y \u003d -1 / fonksiyonunun grafiği kaydırılarak elde edilir. x 2 birim sağa ve 1 birim aşağı. Bu fonksiyonun grafiği bir hiperboldür.

Örnek 2

fonksiyonu çizelim

Yöntem 1'e uygun olarak, örnek 1'deki grafiğin y ≥ 0 olan bölümünü kaydederiz. Grafiğin y için olan bölümü< 0, симметрично отразим вверх относительно оси абсцисс.

Örnek 3

fonksiyonu çizelim

Yöntem 2'yi kullanarak, örnek 1'deki grafiğin x ≥ 0 olan bölümünü kaydedeceğiz. Ek olarak, kaydedilen bu parçayı y eksenine göre sola yansıtacağız. y eksenine göre simetrik olan bir fonksiyon grafiği elde ederiz.

Örnek 4

Denklemin bir grafiğini oluşturalım

Yöntem 3'e göre, örnek 1'deki grafiğin y ≥ 0 olan kısmını kaydediyoruz. Ayrıca kaydedilen bu parçayı apsis eksenine göre simetrik olarak aşağıya yansıtıyoruz. Bu denklemin grafiğini elde ederiz.

Tabii ki, grafikleri dönüştürmek için düşünülen yöntemler birlikte de kullanılabilir.

Örnek 5

fonksiyonu çizelim

Fonksiyonun grafiğini kullanıyoruzBu grafiği oluşturmak için, grafik 3'ün y ≥ 0 olan kısımlarını kaydederiz. Grafik 3'ün y olan kısımlarını kaydederiz.< 0, симметрично отразим вверх относительно оси абсцисс.

Modüllerin farklı bir şekilde bağımlı olduğu durumlarda (yöntem 1-3'ten farklı), bu modüllerin açılması gerekir.

Örnek 6

fonksiyonu çizelim

x - 1 ve x ifadeleri +2 modüllerin işaretleri altına girerek x=1 noktalarında işaretlerini değiştirir ve x = -2 sırasıyla. Bu noktaları koordinat doğrusu üzerinde işaretleyelim. Onu üç aralığa ayırırlar. Modül tanımlarını kullanarak her boşluktaki modülleri genişletelim.

Alırız:

1. Ne zaman

2. Ne zaman

3. Ne zaman

Modülün işaretlerinin ortaya çıktığı x değişkeni için aralıkları dikkate alarak bu fonksiyonların grafiklerini oluşturalım. Kırık bir çizgi alıyoruz.

Oldukça sık, modüllerle denklem grafikleri oluştururken, bunları açmak için bir koordinat düzlemi kullanılır. Bunu aşağıdaki örnekle açıklayalım.

Örnek 7

Denklemin bir grafiğini oluşturalım

y - x ifadesi, y = x düz çizgisinde işaretini değiştirir. Bu düz çizgiyi oluşturalım - birinci ve üçüncü koordinat açılarının açıortayı. Bu çizgi, uçağın noktalarını iki alana böler: 1 - y - x çizgisinin üzerinde bulunan noktalar; 2 - bu çizginin altında bulunan noktalar. Modülü bu tür alanlarda açalım. Alan 1'de, örneğin kontrol noktasını (0; 5) alın. Bu nokta için y - x\u003e 0 ifadesini görüyoruz. Modülü genişleterek şunu elde ederiz: y - x + y + x \u003d 4 veya y = 2. Birinci bölge içinde böyle bir düz çizgi oluşturuyoruz. Açıkça, 2. bölgede, y - x ifadesi< 0. Раскрывая модуль, имеем: -(у - х) + у + х = 4 или х = 2. Строим эту прямую в пределах области 2. Получаем график данного уравнения.

3. Kesirli bir grafik çizin doğrusal fonksiyon ve denklemler:

4. Fonksiyonun, denklemlerin, eşitsizliklerin grafiğini çizin:

VIII. Dersi özetlemek

Transcript

1 6-11. sınıflardaki öğrencilerin eğitim ve araştırma çalışmalarının bölgesel bilimsel ve pratik konferansı "Matematiğin uygulamalı ve temel soruları" Matematik çalışmanın metodolojik yönleri Gabova Anzhela Yurievna modülünü içeren fonksiyon grafiklerinin yapımı, 10. sınıf, MOBU "Gymnasium 3 " Kudymkar, Pikuleva Nadezhda Ivanovna, matematik öğretmeni, MOBU "Gymnasium 3", Kudymkar, Perm, 2016

2 İçindekiler: Giriş...sayfa 3 I. Ana gövde...sayfa 6 1.1 Geçmiş referansı.. 6 s. 2.Fonksiyonların temel tanımları ve özellikleri s.2.1 Kuadratik fonksiyon..7 s.2.2 Doğrusal fonksiyon...8 s.2.3 Kesirli-rasyonel fonksiyon 8 s.Modülün tanımı .. 9 s.3.2 Modüllü doğrusal bir fonksiyonun grafiğini çizmek için algoritma ... 9 s 3.3 Formülde "iç içe modüller" içeren fonksiyonların çizimi 10 s 3.4 y = a 1 x x 1 + biçimindeki fonksiyonların grafiklerini çizmek için algoritma a 2 x x bir n x x n + ax + b...13 s 3.5 Modüllü ikinci dereceden bir fonksiyonun grafiğini çizmek için algoritma.14 s. 3.6 Modüllü kesirli rasyonel bir fonksiyonun grafiğini çizmek için algoritma. 15p. 4. İşaretin konumuna bağlı olarak ikinci dereceden bir fonksiyonun grafiğindeki değişiklikler mutlak değer..17p. II. Sonuç ... 26 sayfa III. Referanslar ve kaynaklar listesi...27 s.IV. Uygulama....28p. 2

3 Giriş Plotting fonksiyonları bunlardan biridir. ilginç konular okul matematiğinde. Zamanımızın en büyük matematikçisi olan Israel Moiseevich Gelfand şöyle yazdı: “Çizim süreci, formülleri ve açıklamaları geometrik görüntülere dönüştürmenin bir yoludur. Bu çizim, formülleri ve işlevleri görmenin ve bu işlevlerin nasıl değiştiğini görmenin bir yoludur. Örneğin, y \u003d x 2 yazılırsa, hemen bir parabol görürsünüz; y = x 2-4 ise, dört birim alçaltılmış bir parabol görürsünüz; y \u003d - (x 2 4) ise, önceki parabolün düştüğünü görürsünüz. Bu formülü bir kerede görme yeteneği ve geometrik yorumu sadece matematik çalışması için değil, aynı zamanda diğer dersler için de önemlidir. Bu, bisiklete binmeyi, yazı yazmayı veya araba kullanmayı öğrenmek gibi bir ömür boyu sizinle birlikte kalan bir beceridir." Modüllerle denklem çözmenin temelleri 6. 7. sınıfta elde edildi. Bu konuyu seçtim çünkü daha derin ve kapsamlı bir çalışma gerektirdiğine inanıyorum. Bir sayının modülü hakkında daha fazla bilgi edinmek istiyorum, çeşitli yollar mutlak değerin işaretini içeren grafikler oluşturmak. Doğruların, parabollerin, hiperbollerin “standart” denklemleri modülün işaretini içerdiğinde, grafikleri olağandışı ve hatta güzel hale gelir. Bu tür grafiklerin nasıl oluşturulacağını öğrenmek için, temel rakamları oluşturma tekniklerinde ustalaşmanız ve ayrıca bir sayının modülünün tanımını kesin olarak bilmeniz ve anlamanız gerekir. Okul matematik dersinde, modüllü grafikler yeterince derinlemesine ele alınmaz, bu yüzden bu konudaki bilgilerimi genişletmek, kendi araştırmamı yapmak istedim. Modülün tanımını bilmeden mutlak bir değer içeren en basit grafiği bile oluşturmak imkansızdır. Karakteristik özellik modulo işaretli ifadeleri içeren fonksiyon grafikleri, 3

4, modül işaretinin altındaki ifadenin işaret değiştirdiği noktalarda bükülmelerin varlığıdır. Çalışmanın amacı: modül işareti altında bir değişken içeren doğrusal, ikinci dereceden ve kesirli rasyonel fonksiyonların bir grafiğinin yapısını düşünmek. Görevler: 1) Doğrusal, ikinci dereceden ve mutlak değerin özellikleri üzerine literatürü incelemek. kesirli rasyonel fonksiyonlar. 2) Mutlak değerin işaretinin konumuna bağlı olarak fonksiyonların grafiklerindeki değişiklikleri araştırın. 3) Denklem grafiklerini çizmeyi öğrenin. Çalışmanın amacı: doğrusal, ikinci dereceden ve kesirli rasyonel fonksiyonların grafikleri. Çalışmanın konusu: Mutlak değerin işaretinin konumuna bağlı olarak doğrusal, ikinci dereceden ve kesirli rasyonel fonksiyonların grafiğindeki değişiklikler. pratik önemi benim işim: 1) konuyla ilgili edinilen bilgileri kullanmak, derinleştirmek ve diğer fonksiyonlara ve denklemlere uygulamak; 2) becerilerin kullanımında Araştırma çalışması gelecekte Öğrenme aktiviteleri. Uygunluk: Grafik ödevleri geleneksel olarak matematikteki en zor konulardan biridir. Mezunlarımız, GIA ve Birleşik Devlet Sınavını başarıyla geçme sorunu ile karşı karşıyadır. Araştırma problemi: GIA'nın ikinci bölümünden modül işaretini içeren fonksiyonların çizilmesi. Araştırma hipotezi: temel alınarak geliştirilen uygulama ortak yollar modülün işaretini içeren fonksiyonların grafiklerini oluşturmak, GIA'nın ikinci bölümünün görevlerini çözme yöntemleri öğrencilerin bu görevleri çözmesine izin verecektir 4

5 bilinçli olarak en akılcı çözüm yöntemini seç, farklı çözüm yöntemleri uygula ve GIA'dan daha başarılı geç. Çalışmada kullanılan araştırma yöntemleri: 1. Bu konudaki matematiksel literatürün ve internet kaynaklarının analizi. 2. Çalışılan materyalin reprodüktif reprodüksiyonu. 3. Bilişsel arama etkinliği. 4. Problemlere çözüm bulmak için verilerin analizi ve karşılaştırılması. 5. Hipotezlerin ifadesi ve doğrulanması. 6. Karşılaştırma ve genelleme matematiksel gerçekler. 7. Elde edilen sonuçların analizi. Bu çalışma yazılırken şu kaynaklardan yararlanılmıştır: İnternet kaynakları, OGE testleri, matematik literatürü. 5

6 I. Ana bölüm 1.1 Tarihsel arka plan. 17. yüzyılın ilk yarısında fonksiyon kavramı, bir değişkenin diğerine bağımlılığı olarak şekillenmeye başlamıştır. Böylece, Fransız matematikçiler Pierre Fermat () ve Rene Descartes () bir eğri noktasının ordinatının apsisine bağımlılığı olarak bir fonksiyon hayal ettiler. Ve İngiliz bilim adamı Isaac Newton () işlevi, zamana bağlı olarak değişen hareket eden bir noktanın koordinatı olarak anladı. "İşlev" terimi (Latince işlev performansı, komisyondan) ilk olarak Alman matematikçi Gottfried Leibniz () tarafından tanıtıldı. Bir fonksiyonu geometrik bir görüntüyle ilişkilendirdi (bir fonksiyonun grafiği). Daha sonra İsviçreli matematikçi Johann Bernoulli () ve bir üye Petersburg Akademisi Bilimler, XVIII yüzyılın ünlü matematikçisi Leonhard Euler (), işlevi analitik bir ifade olarak değerlendirdi. Euler ayrıca, bir değişkenin diğerine bağımlılığı olarak bir fonksiyon hakkında genel bir anlayışa sahiptir. "Modül" kelimesi şuradan gelir: Latince kelimeÇeviride “ölçü” anlamına gelen “modül”. BT çok anlamlı sözcük(eş anlamlı) birçok anlama sahiptir ve sadece matematikte değil, aynı zamanda mimari, fizik, mühendislik, programlama ve diğerlerinde de kullanılır. kesin bilimler. Mimaride bu, belirli bir mimari yapı için oluşturulan ve onun çoklu oranlarını ifade etmek için kullanılan ilk ölçü birimidir. Kurucu unsurlar. Mühendislikte bu, teknolojinin çeşitli alanlarında kullanılan, evrensel bir anlamı olmayan ve çeşitli katsayıları ve miktarları, örneğin, bağlantı modülü, elastiklik modülü vb. belirtmeye hizmet eden bir terimdir. 6

7 Bulk modülü (fizikte), malzemedeki normal gerilmenin bağıl uzamaya oranıdır. 2.Fonksiyonların temel tanımları ve özellikleri Fonksiyon en önemli matematiksel kavramlardan biridir. Bir fonksiyon, y değişkeninin x değişkenine böyle bir bağımlılığıdır; burada, x değişkeninin her bir değeri, y değişkeninin tek bir değerine karşılık gelir. Fonksiyon belirleme yolları: 1) analitik yöntem (fonksiyon matematiksel bir formül kullanılarak ayarlanır); 2) tablo yöntemi (işlev tablo kullanılarak belirtilir); 3) tanımlayıcı yöntem (işlev sözlü bir açıklama ile verilir); dört) grafik yolu(fonksiyon bir grafik kullanılarak ayarlanır). Bir fonksiyonun grafiği, apsisi argümanın değerine eşit olan koordinat düzleminin tüm noktalarının kümesidir ve ordinatlar, fonksiyonun karşılık gelen değerlerine eşittir. 2.1 İkinci dereceden işlev x ve y'nin değişken olduğu ve a, b ve c parametrelerinin herhangi bir gerçek sayı olduğu ve a = 0 olduğu y=ax 2 +in+c formülüyle tanımlanan işleve ikinci dereceden denir. y \u003d ax 2 + in + c fonksiyonunun grafiği bir paraboldür; parabolün simetri ekseni y \u003d ax 2 + + c'de düz bir çizgidir, a> 0 için parabolün “dalları” yukarı doğru yönlendirilir, a için<0 вниз. Чтобы построить график квадратичной функции, нужно: 1) найти координаты вершины параболы и отметить её в координатной плоскости; 2) построить ещё несколько точек, принадлежащих параболе; 3) соединить отмеченные точки плавной линией.,. 2.2Линейная функция функция вида 7

8 (tek değişkenli fonksiyonlar için). Doğrusal fonksiyonların ana özelliği, fonksiyonun artışının argümanın artışıyla orantılı olmasıdır. Yani fonksiyon, doğru orantılılığın bir genellemesidir. Doğrusal bir fonksiyonun grafiği düz bir çizgidir, dolayısıyla adı. Bu, bir gerçek değişkenin gerçek bir işleviyle ilgilidir. 1) Düz çizgi, x ekseninin pozitif yönü ile dar bir açı oluşturur. 2) Doğru, x ekseninin pozitif yönü ile geniş açı oluşturduğunda. 3) doğrunun y ekseni ile kesişme noktasının ordinatının bir göstergesidir. 4) Doğru orijinden geçtiğinde. , 2.3 Bir kesirli-rasyonel fonksiyon, payı ve paydası polinom olan bir kesirdir. Herhangi bir sayıda değişkende polinomların olduğu forma sahiptir. Bir değişkenin rasyonel fonksiyonları özel bir durumdur: nerede ve polinomlardır. 1) Dört aritmetik işlem kullanarak değişkenlerden elde edilebilecek herhangi bir ifade rasyonel bir fonksiyondur. sekiz

9 2) Rasyonel fonksiyonlar kümesi aritmetik işlemler ve kompozisyon işlemi altında kapalıdır. 3) Herhangi bir rasyonel fonksiyon, basit kesirlerin toplamı olarak temsil edilebilir - bu, analitik entegrasyonda kullanılır .., 3. a negatifse, bir modül ile grafikler oluşturmak için algoritmalar. a = 3.2 Modüllü doğrusal bir fonksiyonun grafiğini oluşturmak için algoritma y= x fonksiyonlarının grafiklerini çizmek için, pozitif x için x = x olduğunu bilmeniz gerekir. Bu, argümanın pozitif değerleri için, y=x grafiğinin y=x grafiğiyle çakıştığı anlamına gelir, yani grafiğin bu kısmı, orijinden x'e 45 derecelik bir açıyla çıkan bir ışındır. eksen. x için< 0 имеем x = -x; значит, для отрицательных x график y= x совпадает с биссектрисой второго координатного угла. Впрочем, вторую половину графика (для отрицательных X) легко получить из первой, если заметить, что функция y= x чётная, так как -a = a. Значит, график функции y= x симметричен относительно оси Oy, и вторую половину графика можно приобрести, отразив относительно оси ординат часть, начерченную для положительных x. Получается график:y= x 9

10 İnşaat için (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2) puanları alıyoruz. Şimdi bir y= x-1 grafiği oluşturalım.Eğer A koordinatları (a;a) olan y= x grafik noktası ise, o zaman Y koordinatının aynı değerine sahip y= x-1 grafik noktası A1 noktası olacaktır. (a+1; a). İkinci grafiğin bu noktası, Ox eksenine paralel sağa kaydırılarak birinci grafiğin A(a; a) noktasından elde edilebilir. Bu, y= x-1 fonksiyonunun grafiğinin tamamının, Ox eksenine paralel 1 ile sağa kaydırılarak y= x fonksiyonunun grafiğinden elde edildiği anlamına gelir. Grafikler oluşturalım: y= x-1 Oluşturmak için, (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1) puanlarını alıyoruz. 3.3 Formülde "iç içe modüller" içeren fonksiyonların grafiklerinin oluşturulması Belirli bir örnek kullanarak yapım algoritmasını ele alalım.

11 y \u003d i-2-ix + 5ii 1. Fonksiyonun bir grafiğini oluşturuyoruz. 2. Alt yarım düzlemin grafiğini yukarı doğru OX eksenine göre simetrik olarak gösteriyoruz ve fonksiyonun grafiğini alıyoruz. on bir

12 3. Fonksiyonun grafiğini OX ekseni etrafında simetrik olarak aşağı doğru gösteriyoruz ve fonksiyonun grafiğini alıyoruz. 4. Fonksiyonun grafiğini OX eksenine göre simetrik olarak aşağı doğru gösteriyoruz ve fonksiyonun grafiğini alıyoruz 5. Fonksiyonun grafiğini OX eksenine göre görüntüleyin ve grafiği alın. 12

13 6. Sonuç olarak fonksiyonun grafiği şu şekildedir 3.4. y = a 1 x x 1 + a 2 x x bir n x x n + ax + b biçimindeki fonksiyonların grafiklerini oluşturmak için bir algoritma. Önceki örnekte, modül işaretlerini genişletmek yeterince kolaydı. Daha fazla modül toplamı varsa, alt modül ifadelerinin tüm olası işaret kombinasyonlarını dikkate almak sorunludur. Bu durumda fonksiyonun grafiğini nasıl çizebiliriz? Grafiğin bir çoklu çizgi olduğuna dikkat edin, apsisleri -1 ve 2 olan noktalarda köşeleri vardır. x = -1 ve x = 2 için, alt modül ifadeleri sıfıra eşittir. Pratik bir şekilde, bu tür grafikleri oluşturma kuralına yaklaştık: y \u003d a 1 x x 1 + a 2 x x a n x x n + ax + b biçimindeki bir fonksiyonun grafiği, sonsuz aşırı bağlantılara sahip bir sürekli çizgidir. Böyle bir çoklu çizgi oluşturmak için, tüm köşelerini (köşe apsisleri alt modül ifadelerinin sıfırlarıdır) ve her biri sol ve sağ sonsuz bağlantılarda bir kontrol noktası bilmek yeterlidir. 13

14 Görev. y = x + x 1 + x + 1 fonksiyonunu çizin ve en küçük değerini bulun. Çözüm: 1. Alt modül ifadelerinin sıfırları: 0; -bir; Çoklu çizgi köşeleri (0; 2); (-13); (1; 3).(alt modül ifadelerinin sıfırları denklemde değiştirilir) Bir grafik oluşturuyoruz (Şekil 7), fonksiyonun en küçük değeri modül ile ikinci dereceden bir fonksiyonun grafiğini çizmek için Algoritma Fonksiyon grafiklerini dönüştürmek için algoritmalar hazırlamak. 1. y= f(x) fonksiyonunun grafiğinin oluşturulması. Modülün tanımına göre, bu fonksiyon iki fonksiyona bölünmüştür. Bu nedenle, y= f(x) fonksiyonunun grafiği iki grafikten oluşur: sağ yarı düzlemde y= f(x), sol yarı düzlemde y= f(-x). Buna dayanarak bir kural (algoritma) formüle edebiliriz. y= f(x) fonksiyonunun grafiği, y= f(x) fonksiyonunun grafiğinden şu şekilde elde edilir: x 0'da grafik korunur ve x'de< 0полученная часть графика отображается симметрично относительно оси ОУ. 2.Построение графика функции y= f(x). а). Строим график функции y= f(x). б). Часть графика y= f(x), лежащая над осью ОХ, сохраняется, часть его, лежащая под осью ОХ, отображается симметрично относительно оси ОХ. 14

15 3. y= f(x) fonksiyonunun grafiğini oluşturmak için, önce x> 0 için y= f(x) fonksiyonunun grafiğini çizmelisiniz, sonra x için< 0 построить изображение, симметричное ему относительно оси ОУ, а затем на интервалах, где f(x) <0,построить изображение, симметричное графику y= f(x) относительно оси ОХ. 4.Для построения графиков вида y = f(x)достаточно построить график функции y= f(x) для тех х из области определения, при которых f(х) 0, и отобразить полученную часть графика симметрично относительно оси абсцисс. Пример Построим график функции у = х 2 6х +5. Сначала построим параболу у= х 2 6х +5. Чтобы получить из неё график функции у = х 2-6х + 5, нужно каждую точку параболы с отрицательной ординатой заменить точкой с той же абсциссой, но с противоположной (положительной) ординатой. Иными словами, часть параболы, расположенную ниже оси Ох, нужно заменить линией, ей симметричной относительно оси Ох (Рис.1). Рис Алгоритм построения графика дробно рациональной функции с модулем 1. Начнем с построения графика В основе его лежит график функции и все мы знаем, как он выглядит: Теперь построим график 15

16 Bu grafiği elde etmek için daha önce elde edilen grafiği üç birim sağa kaydırmak yeterlidir. Kesirin paydası x + 3 olsaydı, grafiği sola kaydırırdık: Şimdi fonksiyonun grafiğini elde etmek için tüm koordinatları iki ile çarpmamız gerekiyor. Son olarak, grafiği iki birim yukarı kaydırıyoruz. : Yapmamız gereken son şey, verilen fonksiyonu modülün işareti altındaysa grafiğini çizmektir. Bunu yapmak için, grafiğin koordinatları negatif olan (x ekseninin altında kalan kısım) tüm kısmını simetrik olarak yukarı doğru yansıtırız: Şekil 4 16

17 4. Mutlak değerin işaretinin konumuna bağlı olarak ikinci dereceden bir fonksiyonun grafiğindeki değişiklikler. Y \u003d x 2 - x -3 fonksiyonunu çizin 1) x 0'da x \u003d x olduğundan, gerekli grafik y \u003d 0.25 x 2 - x - 3 parabol ile çakışır.<0, то поскольку х 2 = х 2, х =-х и требуемый график совпадает с параболой у=0,25 х 2 + х) Если рассмотрим график у=0,25 х 2 - х - 3 при х 0 и отобразить его относительно оси ОУ мы получим тот же самый график. (0; - 3) координаты точки пересечения графика функции с осью ОУ. у =0, х 2 -х -3 = 0 х 2-4х -12 = 0 Имеем, х 1 = - 2; х 2 = 6. (-2; 0) и (6; 0) - координаты точки пересечения графика функции с осью ОХ. Если х<0, ордината точки требуемого графика такая же, как и у точки параболы, но с положительной абсциссой, равной х. Такие точки симметричны относительно оси ОУ(например, вершины (2; -4) и -(2; -4). Значит, часть требуемого графика, соответствующая значениям х<0, симметрична относительно оси ОУ его же части, соответствующей значениям х>0. b) Bu nedenle, x için tamamlıyorum<0 часть графика, симметричную построенной относительно оси ОУ. 17

18 Şek. 4 y \u003d f (x) işlevinin grafiği, argümanın negatif olmayan değerleri kümesindeki y \u003d f (x) işlevinin grafiğiyle çakışır ve y'ye göre simetriktir. argümanın negatif değerleri kümesindeki eksen. Kanıt: x 0 ise, f (x) = f (x), yani. argümanın negatif olmayan değerleri kümesinde, y = f (x) ve y = f (x) fonksiyonlarının grafikleri çakışır. y \u003d f (x) çift bir fonksiyon olduğundan, grafiği işletim sistemine göre simetriktir. Böylece, y \u003d f (x) fonksiyonunun grafiği, y \u003d f (x) fonksiyonunun grafiğinden aşağıdaki gibi elde edilebilir: 1. x>0 için y \u003d f (x) fonksiyonunu çizin; 2. x için<0, симметрично отразить построенную часть относительно оси ОУ. Вывод: Для построения графика функции у = f (х) 1. построить график функции у = f(х) для х>0; 2. x için<0, симметрично отразить построенную часть относительно оси ОУ. Построить график функции у = х 2-2х Освободимся от знака модуля по определению Если х 2-2х 0, т.е. если х 0 и х 2, то х 2-2х = х 2-2х Если х 2-2х<0, т.е. если 0<х< 2, то х 2-2х =- х 2 + 2х Видим, что на множестве х 0 и х 2 графики функции у = х 2-2х и у = х 2-2х совпадают, а на множестве (0;2) графики функции у = -х 2 + 2х и у = х 2-2х совпадают. Построим их. График функции у = f (х) состоит из части графика функции у = f(х) при у?0 и симметрично отражённой части у = f(х) при у <0 относительно оси ОХ. Построить график функции у = х 2 - х -6 1) Если х 2 - х -6 0, т.е. если х -2 и х 3, то х 2 - х -6 = х 2 - х

19 Eğer x 2 - x -6 ise<0, т.е. если -2<х< 3, то х 2 - х -6 = -х 2 + х +6. Построим их. 2) Построим у = х 2 - х -6. Нижнюю часть графика симметрично отбражаем относительно ОХ. Сравнивая 1) и 2), видим что графики одинаковые. Работа на тетрадях. Докажем, что график функции у = f (х) совпадает с графиком функции у = f (х) для f(х) >0 ve simetrik olarak yansıyan kısım y \u003d f (x) y'de<0 относительно оси ОХ. Действительно, по определению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий: у = f(х), если f(х) 0; у = - f(х), если f(х) <0 Для любой функции у = f(х), если f(х) >0, sonra f (x) \u003d f (x), bu, bu bölümde y \u003d f (x) fonksiyonunun grafiğinin, y \u003d f (x) fonksiyonunun grafiğiyle çakıştığı anlamına gelir. f(x) ise<0, то f (х) = - f(х),т.е. точка (х; - f(х)) симметрична точке (х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ "отрицательную" часть графика у = f(х). Вывод: действительно для построения графика функции у = f(х) достаточно: 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс. (Рис.5) 19

20 Şekil 5 Sonuç: y= f(x) fonksiyonunu çizmek için 1. y=f(x) fonksiyonunu çizin; 2. Grafiğin alt yarı düzlemde bulunduğu alanlarda, yani f(x)<0, строим кривые, симметричные построенным графикам относительно оси абсцисс. (Рис.6, 7.) 20

21 Fonksiyon grafiklerini çizme üzerine araştırma çalışması y = f (x) Mutlak değerin tanımını ve daha önce ele alınan örnekleri kullanarak, fonksiyon grafiklerini çiziyoruz: y \u003d 2 x - 3 y \u003d x 2-5 x y \u003d x 2-2 ve sonuçlar çıkardı. y = f (x) fonksiyonunun bir grafiğini oluşturmak için aşağıdakiler gereklidir: 1. x>0 için y = f (x) fonksiyonunun bir grafiğini oluşturun. 2. Grafiğin ikinci bölümünü oluşturun, yani oluşturulan grafiği işletim sistemine göre simetrik olarak yansıtın, çünkü bu fonksiyon eşittir. 3. Ortaya çıkan grafiğin alt yarım düzlemde yer alan bölümleri, OX eksenine simetrik olarak üst yarım düzleme dönüştürülmelidir. y \u003d 2 x - 3 fonksiyonunun bir grafiğini oluşturun (modülü belirlemek için 1. yöntem) X< -1,5 и х>1.5 a) y = 2x - 3, x>0 için b) x için<0, симметрично отражаем построенную часть относительно оси ОУ. 2. Строим у = -2 х + 3, для 2 х - 3 < 0. т.е. -1,5<х<1,5 а) у = -2х + 3, для х>0 b) x için<0, симметрично отражаем построенную часть относительно оси ОУ. У = 2 х - 3 1) Строим у = 2х-3, для х>0. 2) OS eksenine göre oluşturulana simetrik düz bir çizgi oluşturuyoruz. 3) Grafiğin alt yarım düzlemde yer alan bölümleri OX ekseni etrafında simetrik olarak görüntülenir. Her iki grafiği karşılaştırdığımızda aynı olduklarını görüyoruz. 21

22 Problem örnekleri Örnek 1. y = x 2 6x +5 fonksiyonunun grafiğini düşünün. x kare olduğundan, x sayısının karesinden sonra işareti ne olursa olsun pozitif olacaktır. Bundan, y \u003d x 2-6x +5 fonksiyonunun grafiğinin, y \u003d x 2-6x +5 fonksiyonunun grafiğiyle aynı olacağı, yani. mutlak değer işareti içermeyen bir fonksiyonun grafiği (Şekil 2). Şekil 2 Örnek 2. y \u003d x 2 6 x +5 fonksiyonunun grafiğini düşünün. Bir sayının modülünün tanımını kullanarak, y \u003d x 2 6 x +5 formülünü değiştiririz. Şimdi bizim için iyi bilinen parçalı bir bağımlılık atamasıyla uğraşıyoruz. Bunun gibi bir grafik oluşturacağız: 1) bir parabol y \u003d x 2-6x +5 oluşturun ve bunun 22 olan kısmını daire içine alın

23, negatif olmayan x değerlerine karşılık gelir, yani. y ekseninin sağındaki kısım. 2) aynı koordinat düzleminde, bir parabol y \u003d x 2 +6x +5 oluşturuyoruz ve bunun x'in negatif değerlerine karşılık gelen kısmını daire içine alıyoruz, yani. y ekseninin solundaki kısım. Parabollerin daire içine alınmış kısımları birlikte y \u003d x 2-6 x +5 fonksiyonunun bir grafiğini oluşturur (Şekil 3). Şekil 3 Örnek 3. y \u003d x 2-6 x +5 fonksiyonunun grafiğini düşünün. Çünkü y \u003d x 2 6x +5 denkleminin grafiği, modül işareti olmayan fonksiyonun grafiğiyle aynıdır (örnek 2'de ele alınmıştır), y \u003d x 2 6 x +5 fonksiyonunun grafiğinin takip ettiğini gösterir. örnek 2'de ele alınan y \u003d x 2 6 x +5 fonksiyonunun grafiğiyle aynıdır (Şekil 3). Örnek 4. y \u003d x 2 6x +5 fonksiyonunun bir grafiğini oluşturalım. Bunu yapmak için, y \u003d x 2-6x fonksiyonunun bir grafiğini oluşturuyoruz. Ondan y \u003d x 2-6x fonksiyonunun grafiğini almak için, parabolün her noktasını negatif bir ordinatla aynı apsisli, ancak zıt (pozitif) ordinatlı bir noktayla değiştirmeniz gerekir. Başka bir deyişle, parabolün x ekseninin altında bulunan kısmı, x ekseni etrafında simetrik bir çizgi ile değiştirilmelidir. Çünkü y \u003d x 2-6x +5 fonksiyonunun bir grafiğini oluşturmamız gerekiyor, o zaman y \u003d x 2-6x olarak düşündüğümüz fonksiyonun grafiğinin sadece y ekseni boyunca 5 birim yukarı kaldırılması gerekiyor (Şek. 4). 23

24 Şekil 4 Örnek 5. y \u003d x 2-6x + 5 fonksiyonunun bir grafiğini oluşturalım. Bunu yapmak için iyi bilinen parçalı işlevi kullanıyoruz. y \u003d 6x +5 6x + 5 \u003d 0 fonksiyonunun sıfırlarını bulun. İki durumu ele alalım: 1) Eğer, o zaman denklem y = x 2 6x -5 şeklini alır. Bu parabolü oluşturalım ve onun olduğu kısmı daire içine alalım. 2) Eğer öyleyse, denklem y \u003d x 2 + 6x +5 şeklini alır. Bu parabolü oluşturalım ve noktanın solunda bulunan kısmını koordinatlarla daire içine alalım (Şekil 5). 24

25 Şekil.5 Örnek6. y \u003d x 2 6 x +5 fonksiyonunu çizelim. Bunu yapmak için y \u003d x 2-6 x +5 fonksiyonunu çizeceğiz. Bu grafiği Örnek 3'te çizdik. Fonksiyonumuz tamamen modül işaretinin altında olduğundan, y \u003d x 2 6 x +5 fonksiyon grafiğini çizmek için, y \u003d x 2 fonksiyonunun grafiğinin her noktasına ihtiyacınız var. 6 x + 5 negatif bir ordinatla, aynı apsise sahip bir nokta ile değiştirin, ancak zıt (pozitif) ordinatla, yani. parabolün Öküz ekseninin altında bulunan kısmı, Öküz eksenine göre simetrik olan bir çizgi ile değiştirilmelidir (Şekil 6). Şekil 6 25

26 II. Sonuç "Matematiksel bilgi, ancak yaratıcı bir şekilde ustalaşılırsa ustaca ve karlı bir şekilde kullanılabilir, böylece öğrenci, ona bağımsız olarak ulaşmanın nasıl mümkün olacağını kendisi görür." BİR. Kolmogorov. Bu görevler, OGE testlerinde çok yaygın olduğu için dokuzuncu sınıf öğrencilerinin büyük ilgisini çekmektedir. Bu fonksiyon grafiklerini oluşturabilmeniz, sınavı daha başarılı bir şekilde geçmenizi sağlayacaktır. Fransız matematikçiler Pierre Fermat () ve Rene Descartes () bir eğri noktasının ordinatının apsisine bağımlılığı olarak bir fonksiyon hayal ettiler. Ve İngiliz bilim adamı Isaac Newton () işlevi, zamana bağlı olarak değişen hareket eden bir noktanın koordinatı olarak anladı. 26

27 III Referanslar ve kaynaklar listesi 1. Galitsky M. L., Goldman A. M., Zvavich L. I. 8. sınıflar için cebir problemlerinin toplanması 9: Proc. okul öğrencileri için ödenek. ve derinleşen sınıflar. ders çalışma Matematik 2. baskı. M.: Aydınlanma, Dorofeev G.V. Matematik. Cebir. Fonksiyonlar. Veri analizi. 9. Sınıf: m34 Proc. genel eğitim çalışmaları için. yönetici 2. baskı, klişe. M .: Bustard, Solomonik V.S. Matematikte soru ve problemlerin toplanması M .: "Lise", Yashchenko I.V. GIA. Matematik: tipik sınav seçenekleri: Seçenekler hakkında.m.: "Milli Eğitim", s. 5. Yashchenko I.V. OGE. Matematik: tipik sınav seçenekleri: Seçenekler hakkında.m.: "Milli Eğitim", s. 6. Yashchenko I.V. OGE. Matematik: tipik sınav seçenekleri: Seçenekler hakkında.m.: "Milli Eğitim", s.

28 Ek 28

29 Örnek 1. y = x 2 8 x Çözüm fonksiyonunu çizin. Fonksiyonun paritesini tanımlayalım. y(-x) değeri, y(x) değeri ile aynıdır, dolayısıyla bu fonksiyon çifttir. O zaman grafiği Oy eksenine göre simetriktir. x 0 için y \u003d x 2 8x + 12 fonksiyonunun bir grafiğini oluşturuyoruz ve grafiği negatif x için Oy'ye göre simetrik olarak gösteriyoruz (Şekil 1). Örnek 2. y \u003d x 2 8x formunun aşağıdaki grafiği Bu, fonksiyonun grafiğinin aşağıdaki gibi elde edildiği anlamına gelir: y \u003d x 2 8x + 12 fonksiyonunun bir grafiğini oluştururlar, grafiğin bir kısmını bırakırlar Ox ekseninin üzerinde yer alan değişmeden kalır ve grafiğin apsis ekseninin altında kalan kısmı Ox eksenine göre simetrik olarak görüntülenir (Şekil 2). Örnek 3. y \u003d x 2 8 x + 12 işlevini çizmek için bir dönüşüm kombinasyonu gerçekleştirilir: y \u003d x 2 8x + 12 y \u003d x 2 8 x + 12 y \u003d x 2 8 x Cevap : Şekil 3. Örnek 4 Modül işaretinin altında duran ifade, x=2/3 noktasında işaret değiştirir. x'te<2/3 функция запишется так: 29

30 x>2/3 için fonksiyon şu şekilde yazılacaktır: Yani x=2/3 noktası koordinat düzlemimizi iki bölgeye ayırır, bunlardan birinde (sağda) fonksiyonu oluştururuz ve diğer (solda) oluşturduğumuz fonksiyonun grafiği: Örnek 5 Sonraki grafik de bozuk, ancak modül işaretleri altında iki ifade içerdiğinden iki kesme noktası var:

31 Birinci aralıktaki modülleri genişletin: İkinci aralıkta: Üçüncü aralıkta: Böylece, (- ; 1.5] aralığında birinci denklemin yazdığı grafiği, aralıkta ikinci denklemin yazdığı grafiği, ve aralıkta)