$A$ olayının olasılığı, $A$ için uygun olan sonuçların sayısının tüm eşit olası sonuçların sayısına oranıdır.
$P(A)=(m)/(n)$, burada $n$ olası sonuçların toplam sayısıdır ve $m$, $A$ lehine olan sonuçların sayısıdır.
Bir olayın olasılığı $$ segmentinden bir sayıdır.
Taksi şirketinin 50$'lık arabası var. 35$'ı siyah, geri kalanı sarı. Rastgele bir çağrıya sarı bir arabanın gelme olasılığını bulun.
Sarı arabaların sayısını bulun:
Toplamda 50$ araba var yani elliden biri çağrıya gelecek. 15$ sarı araba var, bu nedenle sarı arabanın gelme olasılığı $(15)/(50)=(3)/(10)=0.3$
Cevap:$0.3$
Zıt olaylar
Belirli bir denemede uyumsuzsa ve bunlardan biri mutlaka gerçekleşirse, iki olayın zıt olduğu söylenir. Zıt olayların olasılıkları toplamı 1 olur. $A$ olayının tersi bir olay $((A))↖(-)$ olarak yazılır.
$P(A)+P((A))↖(-)=1$
Bağımsız etkinlikler
$A$ ve $B$ olaylarının her birinin gerçekleşme olasılığı diğer olayın oluşup oluşmadığına bağlı değilse bağımsız olarak adlandırılır. Aksi takdirde, olaylar bağımlı olarak adlandırılır.
$A$ ve $B$ adlı iki bağımsız olayın çarpımının olasılığı şu olasılıkların çarpımına eşittir:
$P(A B)=P(A) P(B)$
İvan İvanoviç iki farklı piyango bileti aldı. İlkinin kazanma olasılığı Piyango bileti, 0.15$'a eşittir. İkinci piyango biletinin kazanma olasılığı 0.12 dolar. Ivan Ivanovich her iki çekilişe de katılıyor. Çekilişlerin birbirinden bağımsız yapıldığını varsayarak, İvan İvanoviç'in her iki beraberliği de kazanma olasılığını bulunuz.
Olasılık $P(A)$ - ilk bileti kazanır.
Olasılık $P(B)$ - ikinci bileti kazanır.
$A$ ve $B$ olayları bağımsız olaylardır. Yani her iki olayın da olma olasılığını bulmak için olasılıkların çarpımını bulmanız gerekir.
$P(A B)=P(A) P(B)$
$P=0.15 0.12=0.018$
Cevap: 0,018 $
Uyumsuz etkinlikler
Hem $A$ olayını hem de $B$ olayını destekleyen bir sonuç yoksa, $A$ ve $B$ olaylarının uyumsuz olduğu söylenir. (Aynı anda gerçekleşemeyecek olaylar)
$A$ ve $B$ uyumsuz iki olayın toplamının olasılığı, bu olayların olasılıklarının toplamına eşittir:
$P(A+B)=P(A)+P(B)$
Cebir sınavında öğrenci tüm sınavlardan bir soru alır. Bunun konuyla ilgili bir soru olma olasılığı " ikinci dereceden denklemler", 0,3$'a eşittir. Bunun konuyla ilgili bir soru olma olasılığı " irrasyonel denklemler", 0.18$'a eşittir. Aynı anda bu iki konu ile ilgili soru bulunmamaktadır. Öğrencinin sınavda bu iki konudan birine soru gelme olasılığını bulunuz.
Bu olaylara uyumsuz denir, çünkü öğrenci YA “Dördünlü Denklemler” konusunda VEYA “İrrasyonel Denklemler” konusunda bir soru alır. Konular aynı anda yakalanamaz. $A$ ve $B$ uyumsuz iki olayın toplamının olasılığı, bu olayların olasılıklarının toplamına eşittir:
$P(A+B)=P(A)+P(B)$
$P \u003d 0.3 + 0.18 \u003d 0.48 $
Cevap: $0.48
Ortak Etkinlikler
Birinin meydana gelmesi, aynı davada diğerinin meydana gelmesini engellemiyorsa, iki olayın ortak olduğu söylenir. Aksi takdirde, olaylar uyumsuz olarak adlandırılır.
$A$ ve $B$ adlı iki ortak olayın toplamının olasılığı, bu olayların olasılıklarının toplamı eksi çarpımlarının olasılığına eşittir:
$P(A+B)=P(A)+P(B)-P(A B)$
Sinemanın lobisinde birbirinin aynısı iki kahve makinesi var. Günün sonunda makinenin kahvesinin bitme olasılığı 0,6$'dır. Her iki makinede de kahvenin bitme olasılığı 0,32$'dır. Günün sonunda otomatlardan en az birinin kahvesinin bitmesi olasılığını bulun.
Olayları belirtelim, izin verin:
$A$ = kahve ilk makinede bitecek,
$B$ = kahve ikinci makinede bitecek.
$A B =$ kahve her iki otomatta da bitecek,
$A + B =$ kahve en az bir otomatta biter.
Geleneksel olarak, $P(A) = P(B) = 0.6; P(A B) = 0,32 ABD doları.
$A$ ve $B$ olayları ortaktır, iki ortak olayın toplamının olasılığı, bu olayların olasılıklarının toplamına eşittir, çarpımlarının olasılığı ile azaltılır:
$P(A + B) = P(A) + P(B) − P(A B) = 0,6 + 0,6 − 0,32 = 0,88$
Olasılık. Matematikte profil sınavının görevleri.
MBOU "Lyceum No. 4", Ruzaevka'da bir matematik öğretmeni tarafından hazırlanmıştır.
Ovchinnikova T.V.

olasılığın tanımı
olasılık olaylar A, sayının oranını çağırır m bu olay için olumlu sonuçlar toplam sayısı n tek bir test veya gözlem sonucunda meydana gelebilecek eşit derecede olası uyumsuz tüm olaylar:
m
n
İzin vermek k - yazı tura sayısı, ardından olası sonuçların sayısı: n=2 k .
İzin vermek k - zarların sayısı, ardından olası sonuçların sayısı: sayı=6 k .

Rastgele bir deneyde simetrik bir madeni para iki kez havaya atılıyor. Turaların tam olarak bir kez gelme olasılığını bulun.
Çözüm.
Sadece 4 seçenek: hakkında; oh oh; p p; p p; hakkında .
uygun 2: hakkında; R ve R; hakkında .
Olasılık 2/4 = 1/2 = 0,5 .
Cevap: 0,5.

Rastgele bir deneyde iki zar atılıyor. Toplamda 8 puan alma olasılığını bulun. Sonucu en yakın yüzlüğe yuvarlayın.
Çözüm.
Zarlar 6 tarafı olan zarlardır. İlk kalıp 1, 2, 3, 4, 5 veya 6 puan atabilir. Her puanlama seçeneği, ikinci kalıpta 6 puanlama seçeneğine karşılık gelir.
Şunlar. Toplam Çeşitli seçenekler 6x6=36.
Seçenekler (deneyin sonuçları) aşağıdaki gibi olacaktır:
1; 1 1; 2 1; 3 1; 4 1; 5 1; 6
2; 1 2; 2 2; 3 2; 4 2; 5 2; 6
vb. ................................................
6; 1 6; 2 6; 3 6; 4 6; 5 6; 6
İki zarın puanlarının toplamının 8 olduğu sonuç (seçenek) sayısını sayalım.
2; 6 3; 5; 4; 4 5; 3 6; 2.
Sadece 5 seçenek.
Olasılığı bulalım: 5/36 = 0.138 ≈ 0.14.
Cevap: 0.14.

Biyoloji biletleri koleksiyonunda toplam 55 bilet var, bunlardan 11 tanesi botanikle ilgili bir soru içeriyor. Rastgele seçilen bir sınav biletinde bir öğrencinin botanikle ilgili bir soru alma olasılığını bulun.
Çözüm:
Bir öğrencinin rastgele seçilmiş bir sınav biletinde botanik sorusu alma olasılığı 11/55 = 1/5 = 0,2'dir.
Cevap: 0.2.

Jimnastik şampiyonasına 20 sporcu katılıyor: 8'i Rusya'dan, 7'si ABD'den, geri kalanı Çin'den. Jimnastikçilerin performans sırası kura ile belirlenir. İlk yarışan sporcunun Çin'den olma olasılığını bulun.
Çözüm.
Toplamda 20 sporcu var.
20 - 8 - 7 = Çin'den 5 sporcu.
İlk yarışan sporcunun Çin'den olma olasılığı 5/20 = 1/4 = 0.25'tir.
Cevap: 0.25.

Bilimsel konferans 5 gün sonra yapılır. Toplam 75 rapor planlanmıştır - ilk üç gün, her biri 17 rapor, geri kalanı dördüncü ve beşinci gün arasında eşit olarak dağıtılır. Raporların sırası bir çekilişle belirlenir. Profesör M.'nin raporunun konferansın son gününe planlanma olasılığı nedir?
Çözüm:
Konferansın son günü belirlendi
(75 - 17 × 3) : 2 = 12 rapor.
Profesör M.'nin raporunun konferansın son günü için planlanma olasılığı 12/75 = 4/25 = 0.16'dır.
Cevap: 0.16.

Badminton şampiyonasının ilk turu başlamadan önce, katılımcılar kura ile rastgele oyun çiftlerine ayrılır. Toplamda, Ruslan Orlov da dahil olmak üzere Rusya'dan 10 katılımcı da dahil olmak üzere şampiyonaya 26 badminton oyuncusu katılıyor. Ruslan Orlov'un ilk turda Rusya'dan herhangi bir badminton oyuncusuyla oynama olasılığını bulun?
Çözüm:
Ruslan Orlov'un Rusya'dan bir badminton oyuncusuyla oynaması gerektiğine dikkat edilmelidir. Ve Ruslan Orlov'un kendisi de Rusya'dan.
İlk turda Ruslan Orlov'un Rusya'dan herhangi bir badminton oyuncusuyla oynama olasılığı 9/25 = 36/100 = 0.36'dır.
Cevap: 0.36.

Dasha iki kez atar zar. Toplamda 8 puan aldı. İlk atışta 2 gelme olasılığını bulun.
Çözüm.
Toplamda, iki zar 8 puan atmalıdır. Aşağıdaki kombinasyonlar varsa bu mümkündür:
Sadece 5 seçenek. İlk atışta 2 puanın düştüğü sonuçları (seçenekler) sayalım.
Bu seçenek 1.
Olasılığı bulun: 1/5 = 0.2.
Cevap: 0.2.

Dünya Şampiyonasına katılan 20 takım var. Partilerin yardımıyla, her biri dört takımdan oluşan beş gruba ayrılmaları gerekir. Kutuda grup numaralarına sahip karışık kartlar bulunur:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5.
Takım kaptanları birer kart çeker. Rus takımının üçüncü grupta olma olasılığı nedir?
Çözüm:
Toplamda 20 takım, 5 grup var.
Her grubun 4 takımı vardır.
Yani toplamda 20 sonuç elde ettik, 4'e ihtiyacımız var, bu da istenen sonucun düşme olasılığı 4/20 = 0,2 olduğu anlamına geliyor.
Cevap: 0.2.

İki fabrika aynı camı araba farları için üretiyor. İlk fabrika bu camların %45'ini, ikincisi - %55'ini üretiyor. İlk fabrika kusurlu camların% 3'ünü ve ikinci -% 1'ini üretiyor. Bir mağazadan yanlışlıkla alınan bir bardağın kusurlu olma olasılığını bulunuz.
Çözüm:
Camın ilk fabrikadan alınmış ve kusurlu olma olasılığı:
R 1 = 0.45 0.03 = 0.0135.
Camın ikinci fabrikadan alınmış ve kusurlu olma olasılığı:
R 2 = 0,55 0,01 = 0,0055.
Bu nedenle formüle göre tam olasılık Bir mağazadan yanlışlıkla alınan bir bardağın kusurlu olma olasılığı şuna eşittir:
p = p 1 + p 2 = 0,0135 + 0,0055 = 0,019.
Cevap: 0.019.

Büyük usta A. beyaz oynarsa, büyük usta B.'yi 0,52 olasılıkla kazanır. A. siyah oynarsa, A. B.'yi 0,3 olasılıkla yener.
Büyük ustalar A. ve B. iki oyun oynar ve ikinci oyunda taşların rengini değiştirirler. A.'nın her iki seferde de kazanma olasılığını bulun.
Çözüm:
Birinci ve ikinci oyunları kazanma şansı birbirinden bağımsızdır. Bağımsız olaylar üretme olasılığı, olasılıklarının ürününe eşittir:
p = 0,52 0,3 = 0,156.
Cevap: 0.156.

Biatloncu hedeflere beş kez ateş eder. Hedefi tek atışta vurma olasılığı 0.8'dir. Biatletin ilk üç kez hedefleri vurup son ikisini kaçırma olasılığını bulun. Sonucu en yakın yüzlüğe yuvarlayın.
Çözüm:
Sonraki her atışın sonucu öncekilere bağlı değildir. Bu nedenle, “ilk atışta isabet”, “ikinci atışta isabet” vb. olaylar. bağımsız.
Her isabet olasılığı 0.8'dir. Yani bir kaçırma olasılığı 1 - 0.8 = 0.2'dir.
1 atış: 0.8
2 atış: 0.8
3 atış: 0.8
4 atış: 0.2
5 atış: 0.2
Bağımsız olayların olasılıklarını çarpma formülüne göre, istenen olasılığın şuna eşit olduğunu buluyoruz:
0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 = 0,02048 ≈ 0,02.
Cevap: 0.02.

Mağazanın iki ödeme makinesi var. Diğer otomattan bağımsız olarak her biri 0,05 olasılıkla hatalı olabilir. En az bir otomatın kullanılabilir olma olasılığını bulun.
Çözüm:
Her iki otomatın da hatalı olma olasılığını bulun.
Bu olaylar bağımsızdır, ürünlerinin olasılığı, bu olayların olasılıklarının çarpımına eşittir:
0,05 0,05 = 0,0025.
En az bir otomatın kullanılabilir olması gerçeğinden oluşan bir olay bunun tersidir.
Bu nedenle, olasılığı
1 − 0,0025 = 0,9975.
Cevap: 0.9975.

Kovboy John, bir tabanca ile ateş ederse, 0.9 olasılıkla duvara bir sineğe vurur. John vurulmamış bir tabanca ateşlerse, 0.2 olasılıkla bir sineğe çarpar. Masada sadece 4'ü vurulmuş 10 revolver var. Kovboy John duvarda bir sinek görür, karşısına çıkan ilk tabancayı rastgele alır ve sineğe ateş eder. John'un ıskalama olasılığını bulun.
Çözüm:
John'un bir tabanca alırsa ıskalama olasılığı:
0,4 (1 - 0,9) = 0,04
John'un vurulmamış bir tabanca alırsa ıskalama olasılığı:
0,6 (1 - 0,2) = 0,48
Bu olaylar bağdaşmaz, toplamlarının olasılığı, bu olayların olasılıklarının toplamına eşittir:
0,04 + 0,48 = 0,52.
Cevap: 0.52.

Topçu atışları sırasında otomatik sistem hedefe atış yapar. Hedef yok edilmezse sistem tekrar ateşlenir. Hedef yok edilene kadar atışlar tekrarlanır. İlk atışta belirli bir hedefi yok etme olasılığı 0,4 ve sonraki her atışta 0,6'dır. Hedefi yok etme olasılığının en az 0.98 olmasını sağlamak için kaç atış yapılması gerekecek?
Çözüm:
Bir dizi ardışık ıskadan sonra hayatta kalma olasılığını hesaplayarak sorunu "eylemlerle" çözebilirsiniz:
P(1) = 0.6;
P(2) = P(1) 0.4 = 0.24;
P(3) = P(2) 0.4 = 0.096;
P(4) = P(3) 0.4 = 0.0384;
P(5) = P(4) 0.4 = 0.01536.
Son olasılık 0.02'den azdır, bu nedenle hedefe beş atış yeterlidir.
Cevap: 5.

Sınıfta 26 kişi var, aralarında iki ikiz var - Andrey ve Sergey. Sınıf rastgele 13'er kişilik iki gruba ayrılır. Andrey ve Sergey'in aynı grupta olma olasılığını bulun.
Çözüm:
İkizlerden birinin bir grupta olmasına izin verin.
Onunla birlikte kalan 25 sınıf arkadaşından 12 kişi grupta olacak.
İkinci ikizin bu 12 kişi arasında olma olasılığı eşittir
P=12:25=0.48.
Cevap: 0.48.

Resimde bir labirent görülüyor. Örümcek, "Giriş" noktasında labirentin içine girer. Örümcek dönüp geriye sürünemez, bu nedenle her çatalda örümcek henüz sürünmediği yollardan birini seçer. Diğer yolun seçiminin tamamen rastgele olduğunu varsayarak, örümceğin D'den hangi olasılıkla çıkacağını belirleyin.
Çözüm:
İşaretli dört çatalın her birinde, örümcek ya D çıkışına giden yolu ya da 0,5 olasılıkla başka bir yolu seçebilir. Bunlar bağımsız olaylardır, çarpımlarının olasılığı (örümcek D çıkışına ulaşır) bu olayların olasılıklarının çarpımına eşittir. Bu nedenle, D çıkışına gelme olasılığı (0.5) 4 = 0,0625.
Çözümü, olasılığın klasik bir tanımı olan tek bir formüle dayanan matematikteki (mathege.ru) açık USE problem bankasında bugüne kadar sunulmuştur.
Formülü anlamanın en kolay yolu örneklerle.
örnek 1 Sepette 9 kırmızı, 3 mavi top vardır. Toplar sadece renk olarak farklılık gösterir. Rastgele (bakmadan) bunlardan birini alıyoruz. Bu şekilde seçilen topun mavi olma olasılığı nedir?
Yorum. Olasılık teorisindeki problemlerde bir şey olur ( bu durum topu çekmek için eylemimiz), olabilir farklı sonuç- sonuç. Sonucun farklı şekillerde görülebileceğine dikkat edilmelidir. "Bir top çıkardık" da bir sonuçtur. Sonuç "Mavi topu çıkardık". "Bu özel topu tüm olası toplardan çıkardık" - sonuca ilişkin bu en az genelleştirilmiş görüşe temel sonuç denir. Olasılığı hesaplama formülünde kastedilen temel sonuçlardır.
Çözüm.Şimdi mavi bir top seçme olasılığını hesaplıyoruz.
Olay A: "seçilen top mavi çıktı"
Tüm olası sonuçların toplam sayısı: 9+3=12 (çekebileceğimiz tüm topların sayısı)
A olayı için elverişli sonuçların sayısı: 3 (A olayının gerçekleştiği bu tür sonuçların sayısı - yani mavi topların sayısı)
P(A)=3/12=1/4=0.25
Cevap: 0.25
Aynı problem için kırmızı bir top seçme olasılığını hesaplayalım.
Olası sonuçların toplam sayısı aynı kalacaktır, 12. Olumlu sonuçların sayısı: 9. İstenen olasılık: 9/12=3/4=0.75
Herhangi bir olayın olasılığı her zaman 0 ile 1 arasındadır.
Bazen günlük konuşmada (ama olasılık teorisinde değil!) Olayların olasılığı yüzde olarak tahmin edilir. Matematiksel ve sözlü değerlendirme arasındaki geçiş, %100 ile çarpılarak (veya bölünerek) yapılır.
Yani,
Bu durumda, gerçekleşmesi mümkün olmayan olayların olasılığı sıfırdır. Örneğin, örneğimizde bu, sepetten yeşil bir top çekme olasılığı olacaktır. (Eğer formüle göre sayılırsa olumlu sonuçların sayısı 0, P(A)=0/12=0'dır)
Olasılık 1, seçenekleri olmadan kesinlikle kesinlikle gerçekleşecek olaylara sahiptir. Örneğin, "seçilen topun kırmızı veya mavi olması" olasılığı problemimiz içindir. (Olumlu sonuç sayısı: 12, P(A)=12/12=1)
Olasılığın tanımını gösteren klasik bir örneğe baktık. Hepsi benzer KULLANIM görevleri olasılık teorisine göre bu formül uygulanarak çözülür.
Kırmızı ve mavi topların yerine elma ve armut, kız ve erkek çocuklar, öğrenilmiş ve öğrenilmemiş biletler, bir konuda soru içeren ve içermeyen biletler (prototipler), arızalı ve kaliteli çantalar veya bahçe pompaları (prototipler, ) - ilke aynı kalır.
Teori probleminin formülasyonunda biraz farklı olasılıkları KULLAN, belirli bir günde meydana gelen bir olayın olasılığını hesaplamanız gereken yer. ( , ) Önceki görevlerde olduğu gibi, temel bir sonucun ne olduğunu belirlemeniz ve ardından aynı formülü uygulamanız gerekir.
Örnek 2 Konferans üç gün sürer. Birinci ve ikinci gün 15'er konuşmacı, üçüncü gün - 20. Raporların sırası piyango ile belirlenirse, Profesör M.'nin raporunun üçüncü güne düşme olasılığı nedir?
Buradaki temel sonuç nedir? - Bir profesörün raporunu mümkün olanlardan birine atamak seri numaraları bir performans için. 15+15+20=50 kişi çekilişe katılıyor. Böylece Profesör M.'nin raporu 50 sayıdan birini alabilir. Bu, yalnızca 50 temel sonuç olduğu anlamına gelir.
Olumlu sonuçlar nelerdir? - Profesörün üçüncü gün konuşacağı ortaya çıkanlar. Yani, son 20 sayı.
Formüle göre, olasılık P(A)= 20/50=2/5=4/10=0.4
Cevap: 0.4
Buradaki kura çekimi, insanlar ve düzenli yerler arasında rastgele bir yazışma kurulmasıdır. Örnek 2'de eşleştirme, belirli bir kişinin hangi yerlerden alabileceğine göre değerlendirildi. Aynı duruma diğer taraftan da yaklaşabilirsiniz: belirli bir yere hangi olasılıkla hangi insan ulaşabilir (prototipler , , , ):
Örnek 3Çekilişe 5 Alman, 8 Fransız ve 3 Estonyalı katılıyor. Birincinin (/saniye/yedinci/son - önemli değil) bir Fransız olma olasılığı nedir?
Temel sonuçların sayısı, tüm sonuçların sayısıdır. olası insanlar kim bu yere kura ile ulaşabilir. 5+8+3=16 kişi.
Olumlu sonuçlar - Fransızlar. 8 kişi.
İstenen olasılık: 8/16=1/2=0,5
Cevap: 0,5
Prototip biraz farklı. Madeni paralar () ve zarlar () hakkında biraz daha yaratıcı görevler var. Bu sorunların çözümleri prototip sayfalarında bulunabilir.
İşte bozuk para atma veya zar atma ile ilgili bazı örnekler.
Örnek 4 Yazı-tura attığımızda yazı gelme olasılığı nedir?
Sonuçlar 2 - yazı veya tura. (madeni paranın asla kenara düşmediğine inanılır) Olumlu sonuç - tura, 1.
Olasılık 1/2=0.5
Cevap: 0,5.
Örnek 5 Bir madeni parayı iki kez atarsak ne olur? Her iki seferde de tura gelme olasılığı nedir?
Ana şey, iki madeni parayı atarken hangi temel sonuçları dikkate alacağımızı belirlemektir. İki jeton atıldıktan sonra aşağıdaki sonuçlardan biri ortaya çıkabilir:
1) PP - iki kere yazı geldi
2) PO - ilk tura, ikinci tur tura
3) OP - ilk tura, ikinci tur tura
4) OO - iki seferde de uyarı verir
Başka seçenek yok. Bu, 4 temel sonuç olduğu anlamına gelir.Yalnızca ilki olumlu, 1.
Olasılık: 1/4=0.25
Cevap: 0.25
Bir madeni paranın iki atışının tura gelme olasılığı kaçtır?
Temel çıktıların sayısı aynı, 4. Olumlu çıktılar ikinci ve üçüncü, 2.
Bir kuyruk gelme olasılığı: 2/4=0.5
Bu tür problemlerde başka bir formül işe yarayabilir.
Bir yazı turasında 2 olası sonucumuz varsa, iki sonuç için 2 2=2 2 =4 (örnek 5'te olduğu gibi), üç atış için 2 2 2=2 3 =8, dört için : 2·2·2·2=2 4 =16, … olası sonuçların N atışları için 2·2·...·2=2 N olacaktır.
Böylece, 5 yazı turadan 5 yazı gelme olasılığını bulabilirsiniz.
Temel sonuçların toplam sayısı: 2 5 =32.
Olumlu sonuçlar: 1. (RRRRRR - 5 kez yazıların tümü)
Olasılık: 1/32=0.03125
Aynı şey zar için de geçerlidir. Bir atışla 6 olası sonuç vardır.Yani, iki atış için: 6 6=36, üç atış için 6 6 6=216, vb.
Örnek 6 Bir zar atıyoruz. Çift sayı gelme olasılığı kaçtır?
Toplam sonuç: 6, yüz sayısına göre.
Olumlu: 3 sonuç. (2, 4, 6)
Olasılık: 3/6=0.5
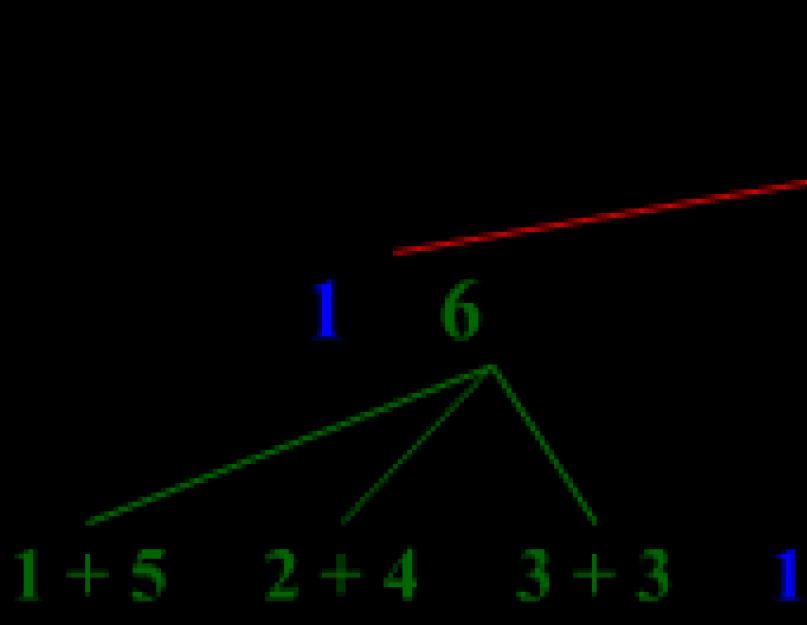
Örnek 7İki zar atın. Toplamın 10 yuvarlanma olasılığı nedir? (yüzde birine yuvarlanır)
Bir zar için 6 olası sonuç vardır. Dolayısıyla, yukarıdaki kurala göre iki kişilik, 6·6=36.
Toplam 10'un düşmesi için hangi sonuçlar olumlu olacak?
10, 1'den 6'ya kadar olan iki sayının toplamına ayrıştırılmalıdır. Bu iki şekilde yapılabilir: 10=6+4 ve 10=5+5. Yani, küpler için seçenekler mümkündür:
(ilkinde 6 ve ikincisinde 4)
(4'ü birinci, 6'sı ikinci)
(birincisinde 5 ve ikincisinde 5)
Toplamda 3 seçenek. İstenen olasılık: 3/36=1/12=0.08
Cevap: 0.08
Diğer B6 sorunları türleri, aşağıdaki "Nasıl Çözülür" makalelerinden birinde tartışılacaktır.
rastgele olay Bazı deneyimlerin bir sonucu olarak meydana gelebilecek veya gelmeyebilecek herhangi bir olay.
Olay Olasılığı R olumlu sonuçların sayısının oranına eşittir k tüm olası sonuçlar arasında. n, yani
p=\frac(k)(n)
Olasılık teorisinin toplanması ve çarpılması için formüller
\bar(A) olayı aranan A olayının tersi, eğer A olayı gerçekleşmediyse.
Olasılıkların toplamı zıt olaylar bire eşittir, yani.
P(\bar(A)) + P(A) =1
- Bir olayın olasılığı 1'den büyük olamaz.
- Bir olayın olasılığı 0 ise o olay olmayacaktır.
- Bir olayın olasılığı 1 ise o olay gerçekleşir.
Olasılık toplama teoremi:
"Uyumsuz iki olayın toplamının olasılığı, bu olayların olasılıklarının toplamına eşittir."
P(A+B) = P(A) + P(B)
olasılık miktarlar iki ortak etkinlik ortak oluşumları dikkate alınmadan bu olayların olasılıklarının toplamına eşittir:
P(A+B) = P(A) + P(B) - P(AB)
Olasılık çarpma teoremi
“İki olayın çarpımının olasılığı, bunlardan birinin olasılıklarının çarpımına eşittir. şartlı olasılık bir diğeri, ilkinin gerçekleşmesi koşuluyla hesaplandı.
P(AB)=P(A)*P(B)
Gelişmeler aranan uyumsuz, birinin görünümü diğerlerinin görünümünü dışlarsa. Yani, yalnızca belirli bir olay veya başka bir olay meydana gelebilir.
Gelişmeler aranan bağlantı, Bunlardan birinin meydana gelmesi diğerinin meydana gelmesine engel olmadıkça.
İki rastgele olay A ve B denir bağımsız, Bunlardan birinin meydana gelmesi, diğerinin meydana gelme olasılığını değiştirmiyorsa. Aksi takdirde, A ve B olaylarına bağımlı denir.