Okomitost u prostoru može imati:

1. Dvije ravne linije

3. Dva aviona

Razmotrimo redom ova tri slučaja: sve definicije i izjave teorema koje se odnose na njih. A onda ćemo raspravljati o vrlo važnoj teoremi o tri okomice.

Okomitost dvije prave.

definicija:

Možete reći: i meni su otvorili Ameriku! Ali zapamtite da u svemiru sve nije isto kao u avionu.

Na ravni samo takve prave (seku) mogu biti okomite:

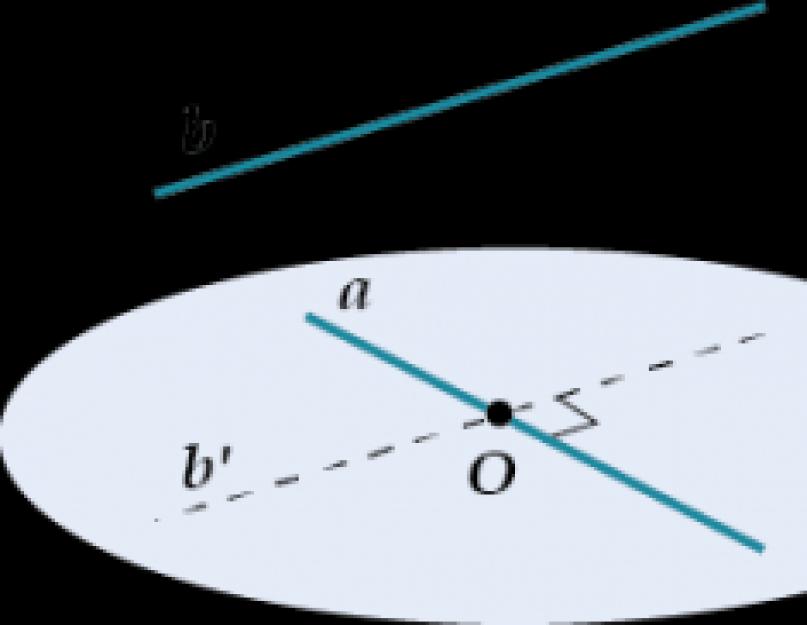
Ali okomitost u prostoru dvije prave može biti čak i ako se ne sijeku. pogledajte:

prava je okomita na pravu, iako je ne siječe. Kako to? Podsjećamo na definiciju ugla između linija: da biste pronašli ugao između kosih linija i, morate povući liniju kroz proizvoljnu tačku na pravoj a. I tada će ugao između i (po definiciji!) biti jednak kutu između i.

Zapamtite? Pa, u našem slučaju, ako se ispostavi da su linije i okomite, onda se linije i trebaju smatrati okomitim.

Da budemo potpuno jasni, pogledajmo primjer. Neka bude kocka. Od vas se traži da pronađete ugao između linija i. Ove prave se ne seku - one se seku. Da biste pronašli ugao između i, nacrtajte.

Zbog činjenice da je - paralelogram (pa čak i pravougaonik!), Ispada da. A zbog činjenice da je - kvadrat, ispada da. Pa, to znači.

Okomitost prave i ravni.

definicija:

evo slike:

prava je okomita na ravan ako je okomita na sve-sve prave u ovoj ravni: i, i, i, pa i! I milijardu drugih linija!

Da, ali kako onda općenito možete provjeriti okomitost u pravoj liniji i ravni? Dakle, život nije dovoljan! Ali, na našu sreću, matematičari su nas spasili od noćne more beskonačnosti tako što su izmislili znak okomitosti prave i ravni.

Formuliramo:

Provjerite kako je odlično:

ako postoje samo dvije prave (e) u ravnini na koju je prava okomita, tada će se ta prava odmah pokazati okomitom na ravninu, odnosno na sve prave u ovoj ravnini (uključujući i neku pravu koja stoji sa strane ). Ovo je veoma važna teorema, pa ćemo i njeno značenje nacrtati u obliku dijagrama.

I pogledajmo ponovo primjer.

Neka nam je dat pravilan tetraedar.

Zadatak: to dokazati. Reći ćete: ovo su dvije prave! Kakve veze ima okomitost prave i ravni s tim?!

ali pogledaj:

označimo sredinu ivice i nacrtajmo i. Ovo su medijane u i. Trouglovi su pravilni i.

Evo ga, čudo: ispostavilo se da je isto tako. I dalje, na sve ravne u ravni, a samim tim i. Dokazano. A najvažnija stvar bila je upravo upotreba znaka okomitosti prave i ravni.

Kada su ravnine okomite

definicija:

Odnosno (za više detalja, pogledajte temu "diedarski ugao"), dvije ravni(e) su okomite ako se ispostavi da je ugao između dvije okomice(e) na liniju presjeka ovih ravni jednak. I postoji teorema koja povezuje pojam okomitih ravni sa konceptom okomitosti u prostoru prave i ravni.

Ova teorema se zove

Kriterijum okomitosti ravnina.

Hajde da formulišemo:

Kao i uvijek, dekodiranje riječi "tada i samo tada" izgleda ovako:

• Ako, onda prolazi kroz okomitu na.

• Ako prolazi kroz okomicu na, onda.

(naravno, ovdje su i avioni).

Ova teorema je jedna od najvažnijih u stereometriji, ali, nažalost, jedna od najtežih za primjenu.

Zato morate biti veoma oprezni!

Dakle, formulacija je:

I opet, dešifrovanje reči "tada i samo tada". Teorema kaže dvije stvari odjednom (pogledajte sliku):

Pokušajmo primijeniti ovu teoremu da riješimo problem.

Zadatak: data je pravilna heksagonalna piramida. Pronađite ugao između linija i.

Rješenje:

Zbog činjenice da u pravilnoj piramidi vrh tokom projekcije pada u centar baze, ispada da je linija projekcija prave.

Ali to znamo u pravilnom šestouglu. Primjenjujemo teoremu o tri okomite:

I napiši odgovor:

PERENDIKULARNOST PRAVA U PROSTORU. UKRATKO O GLAVNOM

Okomitost dvije prave.

Dvije prave u prostoru su okomite ako je ugao između njih.

Okomitost prave i ravni.

Prava je okomita na ravan ako je okomita na sve prave u toj ravni.

Okomitost ravni.

Ravnine su okomite ako je diedarski ugao između njih jednak.

Kriterijum okomitosti ravnina.

Dvije ravni su okomite ako i samo ako jedna od njih prolazi kroz okomicu na drugu ravan.

Teorema o tri okomice:

Pa, tema je gotova. Ako čitate ove redove, onda ste veoma cool.

Zato što je samo 5% ljudi sposobno nešto samostalno savladati. A ako ste pročitali do kraja, onda ste u 5%!

Sada najvažnija stvar.

Shvatili ste teoriju na ovu temu. I, ponavljam, to je... jednostavno je super! Već ste bolji od velike većine svojih vršnjaka.

Problem je što ovo možda nije dovoljno...

Za što?

Za uspješan položen ispit, za upis na institut na budžetu i, NAJVAŽNIJE, doživotno.

Neću vas ni u šta ubeđivati, samo ću jedno reći...

Ljudi koji su stekli dobro obrazovanje zarađuju mnogo više od onih koji ga nisu stekli. Ovo je statistika.

Ali to nije glavna stvar.

Glavna stvar je da su SREĆNIJI (ima takvih studija). Možda zato što se pred njima otvara mnogo više mogućnosti i život postaje svjetliji? ne znam...

Ali razmislite sami...

Šta je potrebno da biste bili sigurni da ćete biti bolji od drugih na ispitu i na kraju biti ... sretniji?

NAPUNI RUKU, RJEŠAVAJUĆI PROBLEME NA OVU TEMU.

Na ispitu vas neće tražiti teorija.

Trebaće ti rješavajte probleme na vrijeme.

A, ako ih niste riješili (PUNO!), sigurno ćete negdje napraviti glupu grešku ili jednostavno nećete to učiniti na vrijeme.

To je kao u sportu - morate ponoviti mnogo puta da biste sigurno pobijedili.

Pronađite kolekciju gdje god želite obavezno sa rješenjima, detaljnom analizom i odluči, odluči, odluči!

Možete koristiti naše zadatke (nije neophodno) i svakako ih preporučujemo.

Da biste nam pomogli uz pomoć naših zadataka, morate pomoći da produžite život YouClever udžbenika koji trenutno čitate.

Kako? Postoje dvije opcije:

1. Otključajte pristup svim skrivenim zadacima u ovom članku -
2. Otključajte pristup svim skrivenim zadacima u svih 99 članaka vodiča - Kupite udžbenik - 899 rubalja

Da, imamo 99 takvih članaka u udžbeniku i pristup svim zadacima i svim skrivenim tekstovima u njima može se odmah otvoriti.

Pristup svim skrivenim zadacima je omogućen za cijeli vijek trajanja stranice.

U zakljucku...

Ako vam se ne sviđaju naši zadaci, pronađite druge. Samo nemojte stati sa teorijom.

“Razumijem” i “Znam kako riješiti” su potpuno različite vještine. Trebate oboje.

Pronađite probleme i riješite ih!

U ovom članku ćemo govoriti o okomitosti prave i ravni. Najprije se daje definicija prave linije okomite na ravan, daje se grafička ilustracija i primjer, a prikazuje se oznaka okomite i ravni. Nakon toga se formuliše znak okomitosti prave i ravni. Dalje, dobijaju se uslovi koji omogućavaju da se dokaže okomitost prave i ravni, kada su prava i ravan date nekim jednačinama u pravougaonom koordinatnom sistemu u trodimenzionalnom prostoru. U zaključku su prikazana detaljna rješenja tipičnih primjera i problema.

Navigacija po stranici.

Okomita prava i ravan - osnovne informacije.

Preporučujemo da prvo ponovite definiciju okomitih pravih, jer je definicija prave okomite na ravan data kroz okomitost pravih.

Definicija.

Kažu to prava prava okomita na ravan, ako je okomita na bilo koju pravu koja leži u ovoj ravni.

Takođe možete reći da je ravan okomita na pravu, ili da su prava i ravan okomite.

Za označavanje okomitosti koristite ikonu obrasca "". Odnosno, ako je pravac c okomit na ravan , onda možemo ukratko napisati .

Kao primjer prave linije koja je okomita na ravan, može se navesti prava linija duž koje se ukrštaju dva susjedna zida prostorije. Ova linija je okomita na ravan i na ravan plafona. Konopac u teretani se takođe može posmatrati kao prava linija okomita na ravan poda.

U zaključku ovog paragrafa članka napominjemo da ako je prava okomita na ravan, onda se ugao između prave i ravnine smatra devedeset stepeni.

Okomitost prave i ravni - znak i uslovi okomitosti.

U praksi se često postavlja pitanje: "Jesu li data prava i ravan okomite?" Da odgovorim, postoji dovoljan uslov za okomitost prave i ravni, odnosno takav uslov, čije ispunjenje garantuje okomitost prave i ravni. Ovaj dovoljan uslov naziva se znakom okomitosti prave i ravni. Formuliramo ga u obliku teoreme.

Teorema.

Da bi data prava bila okomita na ravan, dovoljno je da je prava okomita na dve prave koje se seku u ovoj ravni.

Dokaz znaka okomitosti prave i ravni možete pogledati u udžbeniku geometrije za 10-11 razred.

Prilikom rješavanja zadataka o utvrđivanju okomitosti prave i ravni često se koristi i sljedeća teorema.

Teorema.

Ako je jedna od dvije paralelne prave okomita na ravan, onda je i druga prava okomita na ravan.

U školi se razmatraju mnogi problemi za čije se rješavanje koristi znak okomitosti prave i ravni, kao i posljednja teorema. Ovdje se nećemo zadržavati na njima. U ovom dijelu članka fokusirat ćemo se na primjenu sljedećeg neophodnog i dovoljnog uslova za okomitost prave i ravni.

Ovaj uslov se može prepisati u sljedećem obliku.

Neka je usmjeravajući vektor prave a , i je normalni vektor ravnine . Za okomitost prave a i ravni potrebno je i dovoljno da i : , gdje je t neki realni broj.

Dokaz ovog neophodnog i dovoljnog uslova za okomitost prave i ravni zasniva se na definicijama usmeravajućeg vektora prave i vektora normale ravni.

Očigledno, ovaj uvjet je zgodno koristiti za dokazivanje okomitosti prave i ravni, kada se lako pronađu koordinate usmjeravajućeg vektora prave i koordinate vektora normale ravnine u fiksnom trodimenzionalnom prostoru. . Ovo važi za slučajeve kada su date koordinate tačaka kroz koje prolaze ravan i prava, kao i za slučajeve kada je prava određena nekim jednačinama prave u prostoru, a ravan je data sa jednačina neke vrste ravni.

Pogledajmo nekoliko primjera.

Primjer.

Dokazati da je prava okomita i avioni.

Rješenje.

Znamo da su brojevi u nazivnicima kanonskih jednadžbi ravne u prostoru odgovarajuće koordinate vektora usmjeravanja ove prave linije. Na ovaj način, - vektor pravca pravca .

Koeficijenti na varijablama x, y i z u opštoj jednačini ravnine su koordinate vektora normale te ravni, tj. je normalni vektor ravnine .

Provjerimo ispunjenje potrebnog i dovoljnog uslova za okomitost prave i ravni.

Jer , zatim su vektori i povezani relacijom , odnosno kolinearni su. Dakle, prava linija okomito na ravan.

Primjer.

Jesu li linije okomite? i avion.

Rješenje.

Nađimo vektor pravca date prave i vektor normale ravni da bismo proverili ispunjenje potrebnog i dovoljnog uslova da prava i ravan budu okomite.

Vektor pravca pravca je

Video lekcija 2: Teorema o tri okomice. Teorija

Video lekcija 3: Teorema o tri okomice. Zadatak

Predavanje: Okomitost prave i ravni, znakovi i svojstva; okomito i koso; teorema o tri okomice

Okomitost prave i ravni

Prisjetimo se što je općenito okomitost pravih linija. Okomite su one koje se seku pod uglom od 90 stepeni. U ovom slučaju, ugao između njih može biti, kako u slučaju preseka u određenoj tački, tako i u slučaju ukrštanja. Ako se neke prave sijeku pod pravim uglom, onda se mogu nazvati i okomiti ako se zbog paralelnog prevođenja prava prenese u tačku na drugoj liniji.

definicija: Ako je prava okomita na bilo koju pravu koja pripada ravni, onda se može smatrati okomitom na ovu ravan.

Značajka: Ako na nekoj ravni postoje dvije okomite prave i neka treća prava je okomita na svaku od njih, onda je ova treća prava okomita na ravan.

Svojstva:

• Ako su neke prave okomite na jednu ravan, onda su one međusobno paralelne.

• Ako postoje dvije paralelne ravni, kao i neka prava koja je okomita na jednu od ravnina, onda je i ona okomita na drugu.
• Može se dati i suprotna tvrdnja: ako je određena prava okomita na dvije različite ravni, onda su te ravni nužno paralelne.

koso

Ako neka prava povezuje proizvoljnu tačku koja ne leži na ravni ni sa jednom tačkom na ravni, tada će se takva prava zvati koso.

Imajte na umu da je nagnut samo ako ugao između njega i ravnine nije 90 stepeni.

Na slici, AB je α nagnuta prema ravni. U ovom slučaju, tačka B naziva se osnova nagiba.

Ako povučete segment od tačke A do ravni, koji će sa ravninom činiti ugao od 90 stepeni, tada će se ovaj segment zvati okomica. Okomita se još naziva i najmanja udaljenost od ravnine.

AC je okomica povučena iz tačke A u ravan α. Tačka C naziva se osnova okomice.

Ako je na ovom crtežu nacrtan segment koji će spojiti osnovu okomice (C) sa osnovom kosog (B), tada će se rezultujući segment zvati projekcija.

Kao rezultat jednostavnih konstrukcija, dobili smo pravokutni trokut. U ovom trouglu, ugao ABC se naziva ugao između kose i projekcije.

Teorema o tri okomite

Definicija. Prava koja seče ravan kaže se da je okomita na tu ravan ako je okomita na bilo koju pravu koja leži u datoj ravni i prolazi kroz tačku preseka.
sign okomitost prave i ravni. Ako je prava okomita na dvije prave ravnine koje se seku, onda je ona okomita na datu ravan.
Dokaz. Neka a- prava linija okomita na prave linije b i With koji pripada avionu a. A je tačka preseka pravih. U avionu a Povucite pravu kroz tačku A d, što se ne poklapa sa pravim linijama b i With. Sada ravno a hajde da nacrtamo pravu liniju k, koji siječe linije d i With a ne prolazi kroz tačku A. Tačke preseka, respektivno, D, B i C. Stavite na pravu liniju a u različitim smjerovima od tačke A jednaki su segmenti AA 1 i AA 2. Trougao A 1 CA 2 jednakokraki, jer visina AC je takođe medijana (obeležje 1), tj. A 1 C \u003d CA 2. Slično, u trouglu A 1 BA 2, stranice A 1 B i BA 2 su jednake. Dakle, trouglovi A 1 BC i A 2 BC su jednaki u trećem kriterijumu, pa su uglovi A 1 BD i A 2 BD jednaki. To znači da su trouglovi A 1 BD i A 2 BD također jednaki prema prvom kriteriju. Dakle, A 1 D i A 2 D. Otuda je trougao A 1 DA 2 jednakokraki po definiciji. U jednakokračnom trouglu A 1 D A 2 D A je medijana (po konstrukciji), a samim tim i visina, odnosno ugao A 1 AD je prava, što znači prava linija a okomito na liniju d. Dakle, može se dokazati da je linija a okomito na bilo koju pravu koja prolazi kroz tačku A i koja pripada ravni a. Iz definicije proizlazi da je linija a okomito na ravan a.

Zgrada prava okomita na datu ravan iz tačke uzete izvan ove ravni.
Neka a- ravan, A - tačka iz koje treba spustiti okomicu. Nacrtajte pravu liniju u ravni a. Kroz tačku A i pravu a nacrtati avion b(prava i tačka definišu ravan, i to samo jednu). U avionu b pada iz tačke A na pravu liniju a okomito AB. Iz tačke B u ravni a vratiti okomicu i označiti liniju na kojoj ova okomica leži iza With. Kroz segment AB i pravu liniju With nacrtati avion g(dve prave koje se seku definišu ravan, a samo jedna). U avionu g pada iz tačke A na pravu liniju With okomito AC. Dokažimo da je segment AC okomit na ravan b. Dokaz. Pravo a okomito na prave linije With i AB (po konstrukciji), što znači da je okomito na samu ravan g, u kojem leže ove dvije prave koje se seku (prema kriteriju okomitosti prave i ravni). A pošto je okomita na ovu ravan, onda je i okomita na bilo koju pravu u ovoj ravni, što znači prava a okomito na AC. Prava AC je okomita na dvije prave koje leže u ravni α: With(po konstrukciji) i a(prema dokazanom), znači da je okomita na ravan α (prema kriterijumu okomitosti prave i ravni)

Teorema 1 . Ako su dvije prave koje se seku paralelne sa dvije okomite prave, onda su i one okomite.
Dokaz. Neka a i b- okomite linije a 1 i b 1 - presecane prave linije paralelne s njima. Dokažimo da su linije a 1 i b 1 su okomite.
Ako je ravno a, b, a 1 i b 1 leže u istoj ravni, onda imaju svojstvo naznačeno u teoremi, kao što je poznato iz planimetrije.
Pretpostavimo sada da naše linije ne leže u istoj ravni. Zatim linije a i b leže u nekoj ravni α , a prave a 1 i b 1 - u nekoj ravni β . Na osnovu paralelizma ravni, ravni α i β su paralelne. Neka je C tačka preseka pravih a i b, i S 1 - preseci linija a 1 i b jedan . Nacrtajte u ravni paralelnih pravih a i a a i a 1 u tačkama A i A 1 . U ravni paralelnih pravih b i b 1 ravna linija paralelna pravoj liniji SS 1 . Ona će preći granice b i b 1 u tačkama B i B 1 .
Četvorouglovi CAA 1 C 1 i CBB 1 C 1 su paralelogrami, jer su im suprotne strane paralelne. Četvorougao ABB 1 A 1 je također paralelogram. Njegove stranice AA 1 i BB 1 su paralelne, jer je svaka paralelna pravoj CC 1. Dakle, četvorougao leži u ravni koja prolazi kroz paralelne prave AA 1 i BB 1. I siječe paralelne ravni α i β duž paralelnih pravih AB i A 1 B 1.
Pošto su suprotne strane paralelograma jednake, onda je AB=A 1 B 1 , AC=A 1 C 1 , BC=B 1 C 1 . Trećim znakom jednakosti trouglovi ABC i A 1 B 1 C 1 su jednaki. Dakle, ugao A 1 C 1 B 1, jednak uglu DIA, je ravan, tj. ravno a 1 i b 1 su okomite. Ch.t.d.

Svojstva okomito na pravu i ravan.
Teorema 2 . Ako je ravan okomita na jednu od dvije paralelne prave, ona je također okomita na drugu.
Dokaz. Neka a 1 i a 2 - dvije paralelne prave i α - ravan, okomita na pravu a jedan . Dokažimo da je ova ravan okomita na pravu a 2 .
Kroz tačku A povucite 2 preseka prave a 2 sa ravninom α proizvoljna prava With 2 u α ravni. Povučemo u ravni α kroz tačku A 1 presek prave a 1 sa ravnim α pravolinijom With 1 paralelno sa linijom With 2. Od prave linije a 1 je okomita na ravan α, zatim prave a 1 i With 1 su okomite. A prema teoremi 1, linije koje se seku paralelne su sa njima a 2 i With 2 su također okomite. Dakle, direktno a 2 je okomita na bilo koju pravu With 2 u α ravni. A to znači da je direktno a 2 je okomita na ravan α . Teorema je dokazana.

Teorema 3 . Dvije prave okomite na istu ravan paralelne su jedna s drugom.
Imamo ravan α i dvije prave okomite na nju a i b. Dokažimo to a || b.
Nacrtajte pravu liniju kroz tačke preseka linija ravnine With. Prema znaku koji dobijamo a ^ c i b ^ c. Kroz prave linije a i b nacrtajmo ravan (dvije paralelne prave definiraju ravan i, osim toga, samo jednu). U ovoj ravni imamo dvije paralelne prave a i b i sekansa With. Ako je zbir jednostranih unutrašnjih uglova 180°, tada su prave paralelne. Imamo upravo takav slučaj - dva prava ugla. Zbog toga a || b.

Stalno vidimo da su okomite na istu ravan paralelne. Na primjer, vertikalni segmenti su međusobno paralelni. Ovi segmenti mogu biti predstavljeni paralelnim stupovima ili jarbolima, stablima vitkih borova u brodskoj šumi, stupovima muzejskih zgrada (sl. 84) ili vertikalnim osloncima mostova itd.

Rice. 84

Ova elegantna geometrija je izražena u teoremi koju ćemo sada dokazati.

8.1 Paralelnost pravih okomitih na jednu ravan

Dokaz. Neka su dvije prave a i b okomite na ravan a i sijeku je u tačkama A i B (slika 85). Provučemo ravan p kroz pravu a i tačku B i pokažemo da prava b takođe leži u ravni β.

Rice. 85

U ravni a uzmite odsječak MN okomit na segment AB i čija je sredina tačka A. Kako je AM = AN i AB ⊥ MN, onda je BM = BN.

Uzmimo bilo koju tačku C ≠ B na pravoj b i nacrtajmo segmente CA, CM, CN. Kako je b ⊥ a, trouglovi CBM i CBN su pravougli trouglovi. Oni su jednaki, jer imaju zajedničku nogu CB i jednake krake BM i BN. Stoga je CM = CN, tj. trougao CMN jednakokrak. Njegov srednji CA je također njegova nadmorska visina, tj. CA ⊥ MN.

Dakle, tri prave koje prolaze kroz tačku A - AC, AB i a - su okomite na pravu MN. Po teoremi o ravni okomica (odjeljak 7.2), one leže u istoj ravni - ravni β, koja prolazi kroz prave AB i a.

Kako prava AC leži u ravni β, onda je tačka S ∈ β. Dakle, prava b leži u ravni β (kao i prava a). Ali u ravni β, prave a i b su okomite na istu pravu AB (pošto a ⊥ α, tada b ⊥ α i prava AB leži u α). Stoga b||a.

Dokazana teorema je znak paralelizma pravih u prostoru.

8.2 Paralelno upravno

U ovom pododjeljku dokazujemo teoremu suprotnu teoremi o paralelizmu okomica.

Dokaz. Neka su dvije prave a i b paralelne, a a okomita na ravan a (slika 86). Prava b seče ravan α u nekoj tački B (prema lemi odeljka 3.3). Postoje dvije mogućnosti:

1. b ⊥ α;
2. b nije okomito na α.

Rice. 86

Pretpostavimo da drugi radi. Zatim kroz tačku B povučemo pravu liniju sa ⊥ α (Problem 7.3). Po teoremi o paralelizmu za okomite c||α. Ispostavilo se da dvije prave prolaze kroz tačku B, paralelno sa pravom a, što je nemoguće.

Dakle, b ⊥ α.

Teorema o paraleli na okomicu je još jedan znak okomitosti prave i ravni.

Pitanja za samokontrolu

1. Koje ste znakove paralelnih pravih prepoznali?
2. Koje znakove okomitosti prave i ravni sada poznajete?