Практичні роботи
з математики
1. Знаходження межі функції. Перший і другий чудові межі.
2. Похідна складної функції. Дослідження функції однієї змінної та побудова графіків.
3. Контрольна робота "Застосування диференціального обчислення до дослідження функцій".
4. Знаходження невизначених інтегралів. Обчислення певних інтегралів.
5. Обчислення визначників.
6. Вирішення систем лінійних рівнянь методом Крамера. Контрольна робота.
7. Розв'язання задач на тему «Множини». Формули логіки алгебри.
8. Обчислення ймовірностей випадкових подій. Формула повної ймовірності.
9. Обчислення числових показників.
10. Контрольна робота «Основи теорії ймовірностей та математичної статистики»
11. Тригонометрична форма комплексного числа.
12. Дії з комплексними числами у різних формах.
МЕТОДИЧНІ ВКАЗІВКИ ДО ПРОВЕДЕННЯ ПРАКТИЧНИХ РОБОТ З МАТЕМАТИКИ
2 КУРС
Практичне заняття - це форма організації навчального процесу, що передбачає виконання студентами за завданням та під керівництвом викладача однієї або кількох практичних робіт.
Так, на практичних заняттях з математики у студентів формується вміння вирішувати завдання, яке надалі має бути використане для вирішення професійних завдань із спеціальних дисциплін.
У ході практичних робіт студенти опановують уміння користуватися інформаційними джерелами, працювати з нормативними документами та інструктивними матеріалами, довідниками, виконувати креслення, схеми, таблиці, вирішувати різноманітні завдання, робити обчислення.
Завдання, які вирішуються під час практичних занять з математики:
1) розширення та закріплення теоретичних знань з математики, отриманих у ході лекційних занять;
2) формування у студентів практичних умінь та навичок, необхідних для успішного вирішення задач з математики;
3) розвиток у студентів потреби у самоосвіті та вдосконаленні знань та умінь у процесі вивчення математики;
4) формування творчих відносин та дослідницького підходу в процесі вивчення математики;
5) формування професійно-значимих якостей майбутнього спеціаліста та навичок докладання отриманих знань у професійній сфері.
Практичне заняття №1.Обчислення меж функцій. Перший і другий чудові межі.
Тема : Обчислення меж функцій.
Ціль: придбання базових знань у галузі фундаментальних розділів математики . Перевірка засвоєння знань щодо обчислення меж функцій. Повторити та систематизувати знання з цієї теми.
Завдання:
Розвиток творчого професійного мислення;
Опанування мовою науки, навички оперування поняттями;
Оволодіння вміннями та навичками постановки та вирішення завдань;
Поглиблення теоретичної та практичної підготовки;
Розвиток ініціативи та самостійності студентів.
закріплення обчислювальних навичок;
Продовжити роботу над математичною мовою.
Формування навичок самостійної роботи, роботи з підручником; навички самостійного добування знань;
Розвиток уміння виділяти головне під час роботи з текстом;
Формування самостійності мислення, розумових операцій: порівняння, аналіз, синтез, узагальнення, аналогія;
Показати навчальним роль систематичної роботи з поглиблення та підвищення міцності знань, щодо культури виконання завдань;
Розвиток творчих здібностей учнів.
Забезпечення практичної роботи:
Теоретичний матеріал методичної рекомендації щодо практичної роботи.
Математика, – Серія: Середня професійна освіта. - Ростов-на-Дону «Фенікс», с.
Хід практичного заняття.
1.Формулювання теми заняття, пояснення зв'язку з іншими темами навчальної дисципліни;
2.Перевірка готовності учнів до заняття;
3.Проведення безпосередньо заняття згідно з тематикою та відповідно до робочої програми дисципліни:
Вивчити теоретичний матеріал на тему «Обчислення меж функций».
Розглянути приклади розв'язання типових завдань.
Виконати самостійну роботу з обчислення меж функцій з використанням першої та другої чудової межі.
Відповісти на контрольні питання.
Теоретичні відомості та методичні рекомендації
щодо вирішення завдань.
1. Виклад теоретичного матеріалу.
Щоб обчислити межу функції у точці, треба:
1) Підставити замість змінної x те, чого x прагне.
2) Якщо після виконання пункту 1) отримаємо невизначеність виду, а стрілку замінити на мінус: (x-а).
3) Якщо після виконання пункту 1) отримаємо невизначеність виду, пов'язана зі значеннями тригонометричних функцій. , треба скористатися першою чудовою межею.
Визначення.Першою чудовою межею називається межа
https://pandia.ru/text/78/405/images/image007_4.png" alt="$\displaystyle \lim_(x\to0)\dfrac(\sin x)(x)=1. $" width="102" height="52">!}
5) Визначення:Другою чудовою межеюназивається межа

Число , задане цією межею, грає дуже велику роль як у математичному аналізі, і у інших розділах математики. Число називають основою натуральних логарифмів ( https://pandia.ru/text/78/405/images/image009_4.png" alt="$ e$" width="11" height="14">показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:!}
![]()
2. Закріплення дослідженого матеріалу.
Приклад 1
https://pandia.ru/text/78/405/images/image015_1.png" width="28" height="30 src=">= -4
Ми користувалися правилом 1) і підставили замість x те, чого x прагнути, т. е. x=2.
Приклад 2
https://pandia.ru/text/78/405/images/image017_1.png" width="154" height="32 src=">.png" width="21" height="30 src=">= 5
Приклад 3
https://pandia.ru/text/78/405/images/image021_1.png" width="199" height="37 src=">.png" width="137" height="35 src=">. png" width="138" height="24 src=">=3+3=6
Приклад 4
https://pandia.ru/text/78/405/images/image004_7.png" width="22" height="31 src=">.png" width="104" height="46 src=">. png" height="30 src=">
Приклад 5
https://pandia.ru/text/78/405/images/image032_0.png" width="61" height="46 src=">.png" height="30 src=">=2
Приклад 6
https://pandia.ru/text/78/405/images/image036_0.png" width="18" height="28 src=">
б) 
в) 
3. Закріплення знань, умінь та навичок.
Виконати самостійну роботу з обчислення меж функций.
Практична робота №1. Варіант 1 Обчисліть межу функції: 1. 2. 3. 10. | Практична робота №1. Варіант 2 Обчисліть межу функції: 1. 2. 3. 10. |
Практична робота №2.
Тема : Знаходження похідної функції Дослідження функції однієї змінної та побудова графіка.
Ціль : Перевірити на практиці знання поняття похідної функції, вміння знаходити похідні елементарних функцій, складних функцій, зворотних функцій, користуючись таблицею похідних та правилами диференціювання, поняттям складна та зворотна функція, вміння застосовувати похідну для дослідження функцій.
Забезпечення практичної роботи:
Підручник "Математика". - М.: Дрофа, 2010.
Математика. М:Форум-Інфа 2008.
Індивідуальні картки із варіантом практичної роботи.
1.Теоретичний матеріал та приклади знаходження похідної функції.
Визначення:Похідної функції f(x) (f"(x)) у точці x називається межа відношення збільшення функції до збільшення аргументу при збільшенні аргументу, що прагне до нуля:
https://pandia.ru/text/78/405/images/image061_0.png" width="209 height=235" height="235">
Правила диференціювання.
Якщо у функцій f(x) та g(x) існують похідні, то
2. (u+v)′=u′+v′
3. (uv)′=u′v+v′u
4. (С·u)′=С·u′, де С=соnst
5..png" width="49" height="54 src=">
6. Похідна складної функції:
f′(g(x))=f′(g)·g′(x)
2. Приклади.
1..png" width="61" height="41 src=">.png" width="20" height="41 src=">.png" width="20" height="41 src="> .png" width="69" height="41 src=">+4).
Функція є твір двох множників: u=https://pandia.ru/text/78/405/images/image071_0.png" width="72" height="41 src=">.png" width="64" height="41 src=">.png" width="19" height="41 src=">.png" width="45" height="51 src=">.
Функція є окремим двома виразами: u=https://pandia.ru/text/78/405/images/image079.png" width="52" height="41 src=">..png" width="215 " height="57 src=">.png" width="197 height=36" height="36">
Рішення. Знайдемо похідну цієї функції за правилом диференціювання складної функції (формула 6):

5. Якщо , то 
6. y = x 3 – 3x 2 + 5x+ 2. Знайдемо y "(–1).
y " = 3x 2 – 6x+ 5. Отже, y "(–1) = 14.
7. Якщо y= ln x· cos x, то y" = (ln x) " cos x+ ln x(cos x) " =1/x∙cos x- ln x· sin x.
Нехай дана функція. Для її дослідження необхідно:
1) Знайти її область визначення. Якщо це не надто складно, то корисно знайти також область значень. (Однак, у часто, питання перебування відкладається до перебування екстремумів функції.)
2) З'ясувати загальні характеристики функції, які допоможуть у визначенні її поведінки: чи є функція парної чи непарної, чи вона є періодичною.
3) З'ясувати, як поводиться функція при наближенні аргументу до граничних точок області визначення, якщо такі граничні точки є. Якщо функція має точки розриву, то ці точки теж перевірити наявність вертикальних асимптот функції. Знайти похилі асимптоти.
4) Знайти точки перетину графіка з осями координат, що полягає у простому обчисленні значення функції за умови:
Із віссю ОX: y=0;
З віссю ОY: x = 0.
Знаходження точок перетину з віссю може призвести до необхідності вирішити складне рівняння алгебри, що, можливо, вдасться зробити лише приблизно. Знайшовши коріння функції та точки розриву, ми можемо визначити знак функції кожному з інтервалів між цими точками. Це можна зробити або обчисливши значення функції в якійсь із точок інтервалу, або застосувавши метод інтервалів.
5)Визначити проміжки монотонності. Для цього знаходять похідну та вирішують нерівність:
https://pandia.ru/text/78/405/images/image089.png" width="49" height="19 src=">, функція зменшується.
Знайшовши інтервали монотонності, ми можемо відразу визначити точки локального екстремуму: там, де зростання змінюється зменшенням, розташовуються локальні максимуми, а там, де зменшення змінюється зростанням - локальні мінімуми.
6) Знаходження інтервалів опуклості та увігнутості ведеться за допомогою другої похідної..png" width="39"
якщо https://pandia.ru/text/78/405/images/image090.png" width="39" 0, то крива графіка функції опукла.
Заодно визначаємо точки перегину як точки, у яких функція змінює напрям опуклості (і безперервна).
7) Знаходження точок перетину графіка з асимптотою та додаткових точок. Цей пункт не має обов'язкового характеру, проте знаходження таких точок надає дослідженню функції та побудованому її графіку закінченості та повноти.
Зауважимо, що які у процесі дослідження функції точки на осях координат і графіку корисно відразу ж наносити на креслення. Це допомагає під час усвідомлювати вид графіка.
3. Виконайте самостійно:
|
варіанти | Знайти похідну функції y: |
варіанти | Знайти похідну функції y: |
1. y=6- | 1. y=-6- 5. y= |
||
1. y=-7-1 | 1. y=-7-1 |
||
1.y=4x-3tgx+6x-8 | 1.y=-5x+2ctgx+3x-2 |
||
Цілі уроку:
Навчальна- знати формули диференціювання; правила диференціювання;
диференціювання складної функції; фізичний та геометричний зміст похідної;
рівняння щодо графіку функції.
Розвиваючавміти знаходити похідні функції; вирішувати завдання із застосуванням фізичного сенсу, геометричного сенсу; знаходити значення похідної функції у точці; математично грамотно пояснювати та обґрунтовувати виконувані дії.
Виховна –виховувати самостійність, відповідальність, рефлексію.
Хід уроку
I. Організаційний момент.
ІІ. Перевірка домашнього завдання
(Під час зміни перевіряють консультанти (учнів), з виставленням оцінок).
ІІІ. Постановка мети та мотивація
Вчитель повідомляє учням у тому, що це урок є заключним уроком на тему “Обчислення похідних” і пропонує їм самостійно сформулювати мети.
Учитель: - “Великий філософ Конфуцій одного разу сказав: “Три шляхи ведуть до знання: шлях роздуми - це шлях найблагородніший, шлях наслідування - це найлегший і досвіду - це найгірший”. Так ось сьогодні на уроці кожен з вас визначить яким шляхом до знання даної теми він знаходиться”.
Перед учнями ставиться завдання - показати свої знання та вміння з обчислення похідних та повідомляється план уроку.
І етап:Виконання завдання за карткою "Згадай".
(перевірка знань формул та правил диференціювання).
ІІ етап:Усна фронтальна робота на повторення та узагальнення знань.
III етап:"Тест-прогноз" (при виконанні цього завдання допустима допомога консультантів).
IV етап:Розв'язання практичного завдання.
V етап:Самостійна робота
Оцінюються I, III, V етапи роботи та домашнє завдання. Перевіряють та вносять результати в оціночну таблицю консультанти.
Критерії оцінок: «5»- 19-20 балів;
«4»- 15-18 балів;
«3»– 10-14 балів.
Шляхи до знання
- Відтворення та корекція опорних знань
І етап.
Ціль:контроль, самоконтроль знань формул та правил диференціювання
Згадай! Ф.І. __________________________________________________ |
|
Похідна |
|
c,c - cons t |
|
|
|
|
|
f"(x)+ g"(x) |
|
f(x)* g(x) |
|
|
|
По закінченню цього завдання виконується самоперевірка по Таблиці похідних. Картки здаються консультантам на перевірку (виправлення карток не допускаються).
V. Узагальнення та систематизація знань
ІІ етап.
1.Усна фронтальна робота.
А.Сформувати завдання до цієї умови та вирішити його.
![]()
1. Знайти значення похідної функції у точці t = 3. (Відповідь: 21.)
2. Скласти рівняння дотичної до графіка функції у точці t = 3. (Відповідь: у = 21х-45.).
3. Знайти швидкість руху тіла та прискорення в момент часу t = 3c, якщо закон руху заданий формулою. (Відповідь: 21м/c, 16 м/с²).
4. Знайти кутовий коефіцієнт дотичної, проведеної графіку функції у точці t = 3. (Відповідь: 21.).
5. Знайдіть тангенс кута нахилу дотичної до графіка функції у точці t = 3 і визначте вид кута між дотичним та позитивним напрямком осі Ox. (Відповідь: tgα, кут α – гострий)
З. Знайдіть похідні функцій

2. III етап"Тест-прогноз"


Після закінчення цього завдання виконується самоперевірка за підсумковими відповідями та тести здаються консультантам. (Виправлення в картках не допускаються).
Відповіді:
1 варіант |
||||
2 варіант |
- Рішення завдання
IV етап
Фронтальне розв'язання задачі підвищеного рівня (рішення виконують консультанти спільно з класом).
Завдання
При яких значеннях параметра aдотичні до графіку функції ![]()
проведені в точках його перетину з віссю X утворюють між собою кут 60°?

Графіком є парабола з гілками вгору, що перетинають вісь X у двох точках (випадок a=0 не задовольняє змісту задачі):
IX. Підбиття підсумків та виставлення оцінок
1. Запитання: а) Чи виконано мету уроку?
б) Який етап видався найскладнішим?
в) Що було найцікавішим?
2. Консультанти озвучують результати (кількість та прізвище учнів на шляху
наслідування, шляхи роздуми та шляхи досвіду).
Практичне заняття
Тема:Знаходження похідних. Застосування похідної до дослідження функції та побудови графіків.
Ціль: Освоїти обчислення похідних, навчитися досліджувати функцію за допомогою похідної
Засоби навчання:зошити для виконання практичних занять, презентації на тему, Інтернет-ресурси.
1. Розгляньте теоретичний матеріал на теми: «Правила обчислення похідних», «Екстремум функції», «Випуклість, увігнутість. Крапка перегину».
2. Розгляньте зразки виконання завдань.
3. Виконайте тестове завдання №1.
Контрольні питання:
1. Дайте визначення максимуму (мінімуму) функції у точці. Що можна сказати про знак збільшення функції в досить малій околиці точки максимуму (мінімуму)?
2. Які необхідні умови для існування екстремуму функції? Який їхній геометричний зміст?
3. Яке правило знаходження найбільшого та найменшого значень функції на відрізку?
4. Дайте визначення опуклості (увігнутості) кривої на проміжку.
5. Яке правило відшукання інтервалів опуклості та увігнутості кривої?
6. Точка перегину кривої. Як його знайти?
7. Який алгоритм побудови графіка функції?
Правила обчислення похідних
Похідна складна функція.
Якщо у=ƒ( і), і = φ(х), то у¢ ( х)=ƒ¢ (і)·φ¢ (х).
Похідна сума.
Якщо у(х)=і(х)+v (х), то у¢ (х)=і¢ (х)+v ¢ (х)
Похідні твори.
Якщо у(х)=і(х)· v (х), то у¢ = і¢ · v + u · v ¢ .
Зокрема, ( з· і)¢ = с· і¢, тобто постійний множник виноситься з-під знаку похідної. Легко переконатися, що
(u 2 ) ¢ = 2 u·u ¢ , (u 3 ) ¢ =3u 2 ·u ¢ , … , (u n ) ¢ =n·u n-1 ·u ¢ .
Похідна приватного.
Якщо то  .
.
Таблиця похідних
1. (с)¢ =0
Для складної функції: якщо і=і(х), то:
2. (х)¢ =1
3. (х α )¢ = α · хα–1 , а- Будь-яке дійсне число.
 .
.
3. 

4. (а х ) ¢ =а х · ln а
4. 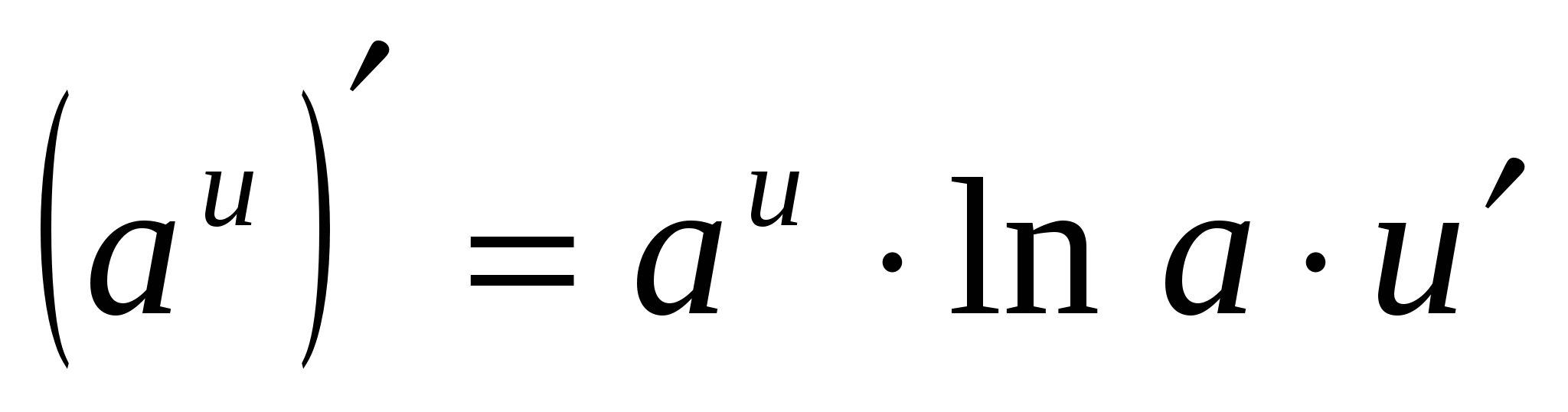

5. (log
a
x)
¢
=
 .
.
5. 

6. (sin x)¢ =cos x
6. 
7. (cos x)¢ = -sin x
7. 
8. (tg x)¢
=
8. 
9. (ctg x)¢
=
9. 
10. 
10. 
11. 
11. 
12. 
12. 
13. 
13. 
Розгляньте приклади
приклад 1.
у = (3-2 sin 5x) 4 | Застосовуємо формули похідних для і α , sin u |
y ¢ =4·(3–2·sin5x) 3 ·(3–2sin5x) ¢ =4·(3–2·sin5x) 3 · (0-2 · cos5x · 5) = -40 · (3-2 · sin5x) 3 .
приклад 2.
. 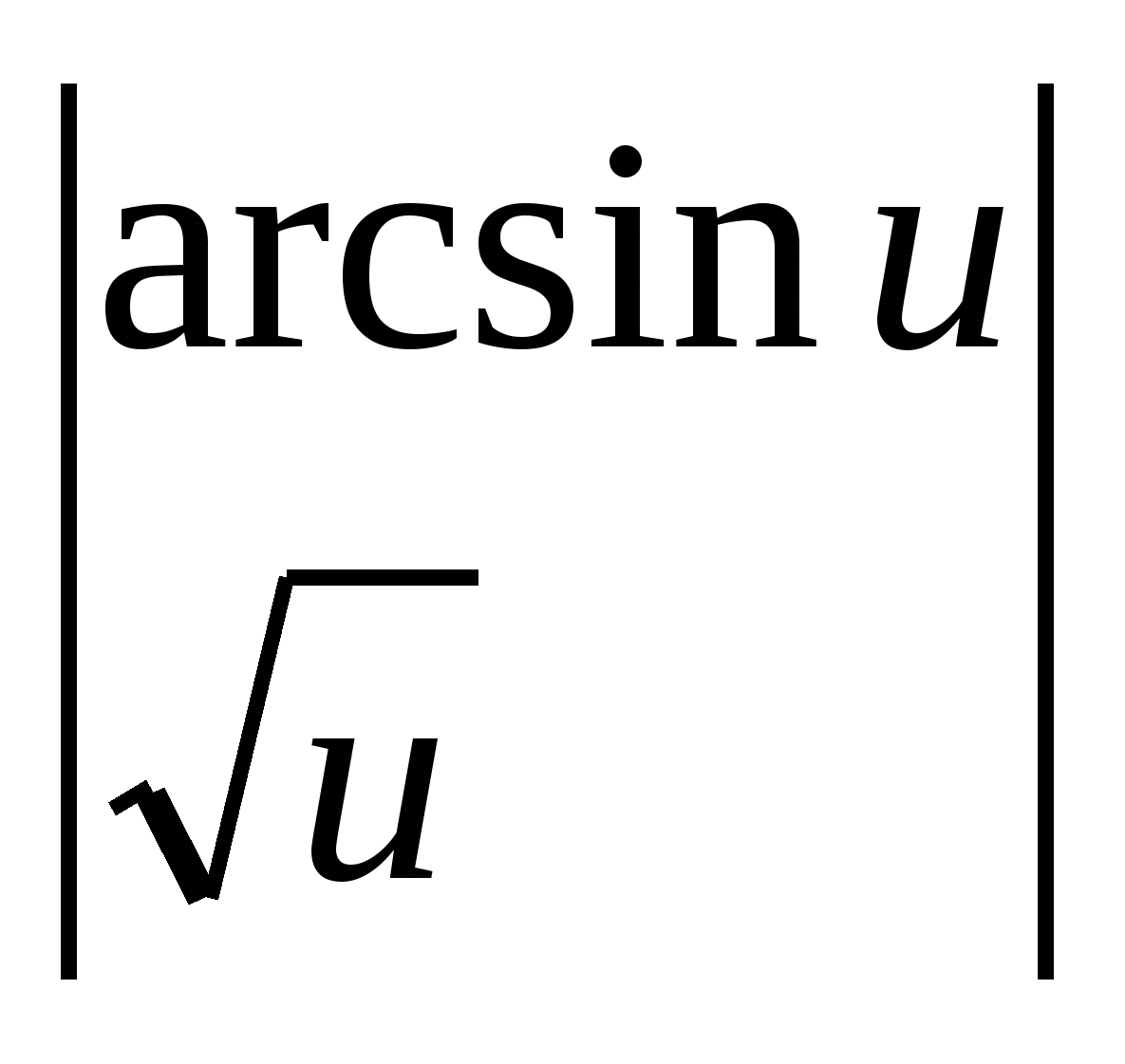

приклад 3.
 .
. 

приклад 4.



Приклад 5.
 .
. 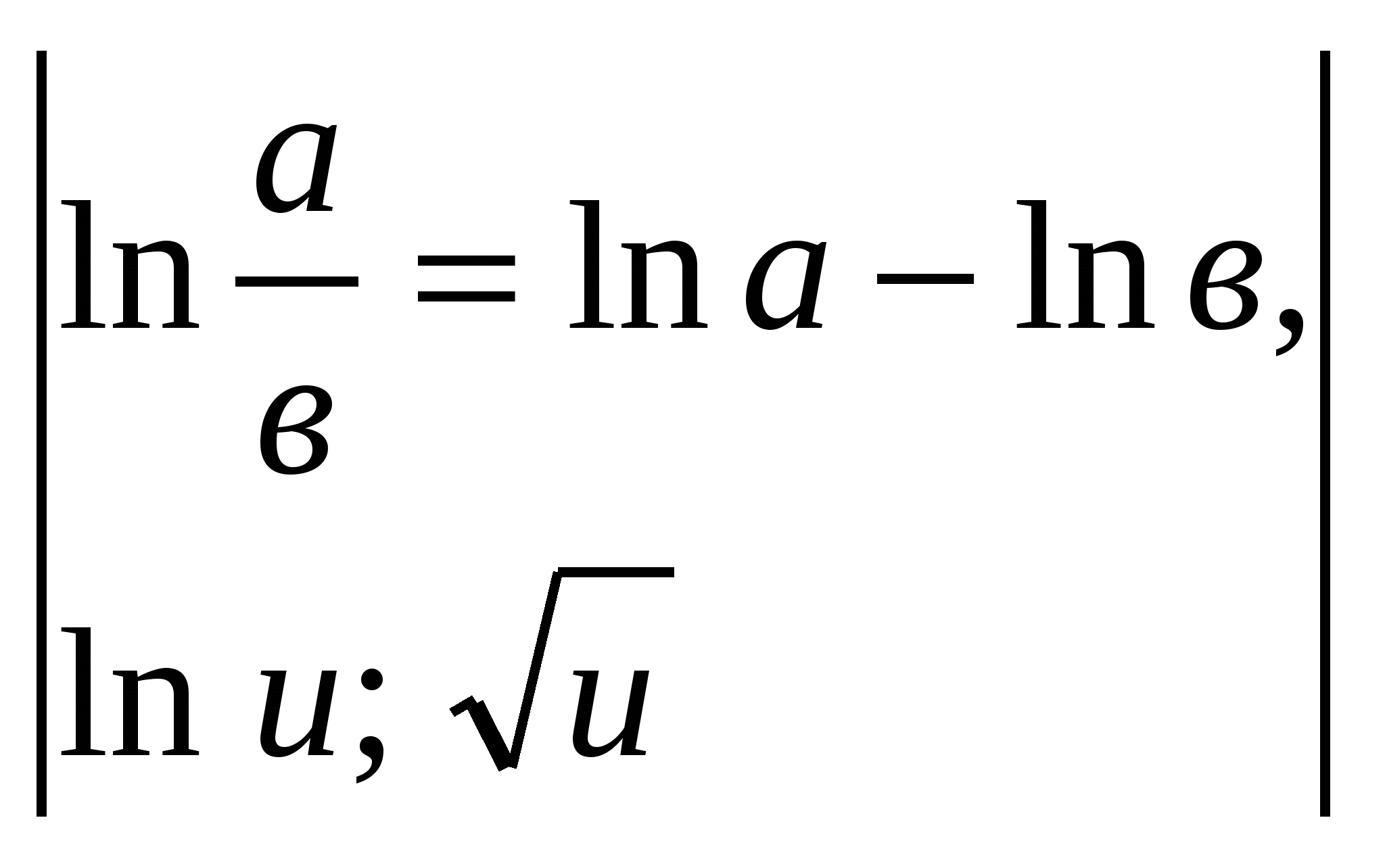

Екстремум функції
Дослідження функції на екстремум - одна з найважливіших додатків похідних. Розглянемо визначення мінімумів і максимумів, і методи їх пошуку.
Нехай функція ƒ( х) визначена і диференційована на деякій множині і точка х 0 – точка усередині нього.
Визначення.Функція ƒ (х) у точці х 0 має максимум(мінімум), якщо існує така околиця точки х 0 , що для всіх хз цієї околиці ƒ (х) < ƒ (х 0 ) (ƒ (х) > ƒ (х 0 )).
Крапка х 0 називається тоді точкою максимуму(мінімуму).

Мал. 1.
Показано графік функції, яка має дві точки максимуму ( х 1 та х 3) та дві точки мінімуму ( х 2 та х 4), причому максимальне значення може виявитися менше мінімального ( ƒ (х 1 ) < ƒ (х 4)). Це підкреслює те що, що ми характеризуємо особливість функції лише поблизу деякої точки.
Значення функції в точках максимуму та мінімуму називають екстремальними значеннями або екстремумами. На наведеному графіку видно, що точки екстремуму ( х 1 , х 2 , х 3 , х 4) визначають інтервали монотонності функції, у кожному з яких похідна зберігає певний знак. У точках екстремуму, зрозуміло, похідна перетворюється на нуль. Сформулюємо теорему про необхідній умові існування екстремуму.
Теорема.Якщо функція ƒ (х) у точці х 0 має екстремум, то похідна функції у цій точці дорівнює нулю, тобто ƒ¢ ( х 0)=0.
Зауважимо відразу, що це не є достатнім, т. е. зворотне твердження який завжди правильне. З рівності ƒ ¢ ( х 0)= 0 не обов'язково слідує, що в точці х 0 існує екстремум.
Підтвердженням тому приклад із функцією ƒ (х)=х 3 .
Знайдемо ƒ ¢ ( х)= 3х 2 . У точці х=0 ƒ ¢ (0)=0 . Але як завгодно близько до точки х=0 знайдемо х> 0, де ƒ (х)=х 3 > 0, знайдемо х< 0, где ¦ (х)=х 3 < 0. Т. е. не существует какая-либо малая окрестность точки х=0, де всім хзначення функції у точці х=0 буде найбільшим або найменшим. Тому точка х=0 не є точкою екстремуму.
Можна міркувати інакше. Оскільки похідна ƒ ¢ (х) = 3х 2 , то функція ƒ(х)=х 3 зростає за будь-яких дійсних х та екстремумів не має.
Точки, в яких виконується необхідна умова екстремуму (ƒ ¢ (х) = 0)називаються критичними .
Очевидно, що стосується графіку функції в точках, де ƒ ¢ (х) = 0,паралельна осі абсцис Ох .
Достатня умоваекстремуму дається у наступних теоремах.
Теорема 1.Якщо х 0 - критична точка функції і при переході через неї похідна змінює знак, то х 0 – точка екстремуму, а саме, якщо похідна змінює знак із плюсу на мінус – точка максимуму, якщо – з мінуса на плюс – точка мінімуму.
Зауважимо, що екстремуму в точці немає, якщо похідна не змінює знаку. Правило дослідження на екстремум за допомогою першої похідної відоме зі шкільного курсу. Достатню умову екстремуму іноді зручніше формулювати за допомогою другої похідної.
Нехай функція ƒ( х) двічі диференційована в деякій області (тобто ƒ( х) має ƒ¢ ( х) та ƒ ¢¢ ( х)).
Теорема 2.Якщо х 0 – критична точка функції ƒ(х)та ƒ ¢¢ (х 0 ) > 0 , то х 0 – точка мінімуму, якщо ƒ ¢¢ (х 0 ) < 0, то х 0 – точка максимуму.
За допомогою другої похідної визначається опуклість або увігнутість графіка функції.
Випуклість, увігнутість. Точка перегину.
Крива у=ƒ(х) називається опуклой нижчебудь-який її дотичної
ƒ ¢¢ ( х) < 0.
Крива у=ƒ(х) називається увігнутою на інтервалі, якщо всі точки кривої лежать вище будь-який її дотичної у цьому інтервалі. Тоді на цьому інтервалі
ƒ ¢¢ (х) > 0
Визначення. Точкою перегину кривою називається точка, з одного боку від якої крива опукла, з іншого увігнута.
У точці перегину ƒ ¢¢ ( х)=0.
Отже, знак другої похідної (як і символ самої функції та її першої похідної) свідчить про особливості графіка функції. Ще раз зупинимося на них.
Якщо для всіх хна інтервалі ( а, b) ƒ (х) > 0 (ƒ (х) < 0), то графік лежить вище (нижче) осі абсцис.
Якщо для всіх хна інтервалі ( а, b) ƒ ¢ ( х) > 0 (ƒ ¢ ( х) < 0), то функция на (а, b) Зростає (зменшується).
Якщо для всіх хна інтервалі ( а, b) ƒ ¢¢ ( х) > 0 (ƒ ¢¢ ( х) < 0), то график на (а, b) увігнутий (опукл).
Рівняння ƒ( х)=0 визначає «нулі» функції, тобто точки перетину графіка з віссю Ох.
Рівняння ƒ ¢ ( х)=0 визначає критичні точки.
Рівняння ƒ ¢¢ ( х)=0 визначає можливі точки перегину.
Схема дослідження функції
Для дослідження функції ƒ (х) та побудови графіка у=ƒ(х) слід знайти:
1) область визначення функції та точки перетину графіка з осями координат;
2) інтервали монотонності;
3) точки екстремумів та значення функції у цих точках;
4) інтервали опуклості та увігнутості графіка;
5) точки перегину графіка;
6) побудувати в декартовій системі координат усі отримані точки (іноді, для уточнення графіка отримують додаткові точки) і сам графік.
Найменше та найбільше значення функції на відрізку
При вирішенні деяких завдань методу оптимізації важливо вміти знаходити найменше чи найбільше значення функції деякому відрізку. Ці значення функція досягає або критичних точках, або кінцях відрізка.
Схема відшуканнянайменшого та найбільшого значень функції ƒ (х) на відрізку [ а, b].
1. Знайти похідну функції ƒ ¢ ( х).
2. Знайти критичні точки із рівняння ƒ ¢ ( х)=0.
3. Вибрати ті критичні точки, які належать даному відрізку [ а, b] та знайти значення функції ƒ (х) у кожній такій точці.
4. Обчислити значення функції ƒ (х) на кінцях відрізка: ƒ( а) та ƒ( b).
5. З отриманих значень функції вибрати найбільше (найбільше) і найменше (найменше).
приклад 2.
Знайти найбільше та найменше значення функції ƒ(х)=х 3 -9х 2 +24х-10на відрізку.
1. ƒ ¢ ( х)= 3х 2 – 9·2 х 2 + 24.
2. ƒ ¢ ( х)=0, 3(х 2 –6х+8)=0, х 1 =2, х 2 =4.
3. Точка х 2 =4 не належить відрізку. Тому обчислимо значення функції лише у точці х 1 =2
ƒ(2)=2 3 –9·2 2 +24·2–10=10.
4. Значення функції на кінцях відрізка: ƒ(0)= –10, ƒ(3)=3 3 –9·3 2 +24·3–10, ƒ(3)=8.
5. Отримано значення:
ƒ(2)=10, ƒ(0)= –10, ƒ(3)=8.
Найбільше значення дорівнює 10 і досягається у точці х=2. Найменше – одно –10 і досягається у точці х=0.
приклад 3.
Знайти інтервали опуклості та увігнутості та точки перегину кривої у=х+36х 2 –2х 3 –х 4 .
Областью визначення цієї функції є безліч всіх дійсних чисел, тобто. хЄ(–∞, +∞).
Знайдемо другу похідну.
у¢ =1+72 х–6х 2 –4х 3 .
у¢¢ =72–12 х–12х 2 = –12(х 2 +х–6).
З рівняння у¢¢ =0 отримаємо абсцис точки перегину:
–12(х 2 +х–6)=0 х 1 = –3; х 2 =2.
Визначимо знак у¢¢ на інтервалах
(–∞; –3), (–3; 2), (2, +∞).
х
(–∞, –3)
(–3; 2)
(2; +∞)
у¢¢
форма кривої
опукла
перегин
увігнута
перегин
опукла
Знайдемо ординати точок перегину:
у(–3)=726; М 1 (–3; 726) – точка перегину
у(2)=114; М 2 (2; 114) – точка перегину.
На інтервалі (–3; 2) крива увігнута. На інтервалах (–∞; –3) та (2; +∞) – опукла.
Зразки виконання завдань
Завдання №1.
Знайти точки розриву функції та побудувати графік

Функція ƒ (х) визначена для всіх дійсних хі безперервна на кожному із зазначених проміжків: (–∞; –1), [–1; 0], (0, +∞). Досліджуємо функцію ƒ (х) на безперервність у точках х= -1 і х=0.
Для цього в кожній із цих точок знайдемо односторонні межі.

Оскільки односторонні межі різні, то х = –1 – точка розриву першого роду.

Односторонні межі рівні, тобто в точці х = 0 існує межа функції і 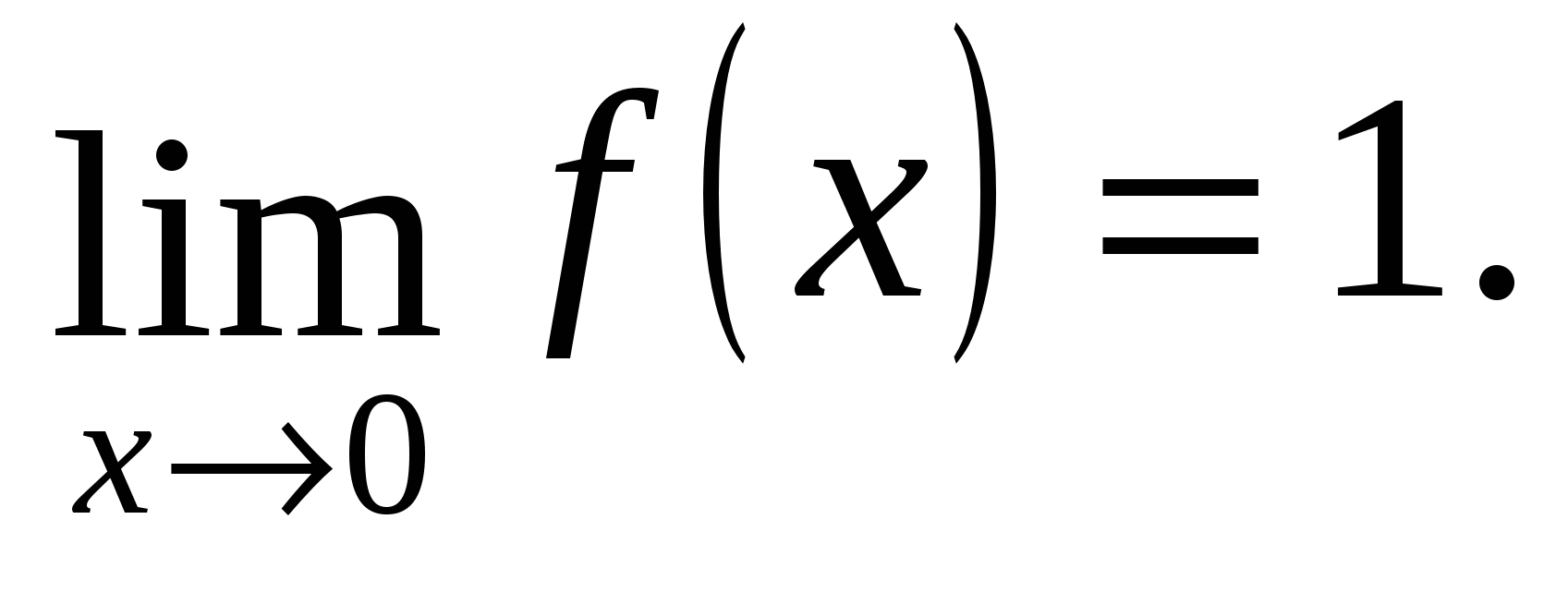
Порівняємо цю межу зі значенням функції у точці: 
Так як  то в точці х = 0 функція ƒ (х) безперервна.
то в точці х = 0 функція ƒ (х) безперервна.
Побудуємо графік функції ƒ (х), враховуючи що
1)  - Рівняння прямої,
- Рівняння прямої,
2)  - Рівняння верхнього півкола
- Рівняння верхнього півкола  з центром на початку координат і радіусом, що дорівнює одиниці, а за умови –1 £ х£ 0 рівняння
з центром на початку координат і радіусом, що дорівнює одиниці, а за умови –1 £ х£ 0 рівняння  визначає чверть кола.
визначає чверть кола.
3) для х > 0 графік задається рівнянням  . Крапки перетину цієї кривої з віссю Ох знайдемо з рівняння
. Крапки перетину цієї кривої з віссю Ох знайдемо з рівняння  при x > 0. x = π
n, де n
=1, 2, 3, 4,
при x > 0. x = π
n, де n
=1, 2, 3, 4,

Мал. 2.
Завдання №2.
Скласти рівняння дотичних до лінії  у точках, де х=0 і х=4. Знайти точку перетину дотичних і кут між ними. Зробити креслення.
у точках, де х=0 і х=4. Знайти точку перетину дотичних і кут між ними. Зробити креслення.
Рівняння дотичної до лінії у=ƒ(х)має вигляд
де у 0 =ƒ( х 0).
У точці х=0 у(0) = ƒ (0) = 5.
у¢ =ƒ ¢ (х)=х–3 ƒ¢ (0)= –3.
М 1 (0, 5) має вигляд у– 5= –3(х-0) або
у= –3х+5.
У точці х=4 у(4) = ƒ (4) = 1. ƒ¢ (4)=4–3=1.
Рівняння дотичної у точці М 2 (4, 1) має вигляд у– 1=х-4 або
у=х–3.
Точку перетину дотичних отримаємо, вирішивши систему

Точка перетину М 3 (2, –1).
Кут φ між дотичними знайдемо з формули:
 ,
,
де k 1 = –3; k 2 = 1 - кутові коефіцієнти дотичних.
 .
.
Кут φ = arctg 2.
Побудуємо цю лінію  – параболу з вершиною у точці, де х=3, т. до. у¢
=0 при х=3. Знайдемо
– параболу з вершиною у точці, де х=3, т. до. у¢
=0 при х=3. Знайдемо  . Крапка М 4 (3;
. Крапка М 4 (3;  ) – вершина параболи.
) – вершина параболи.
Р 
іс. 3.
Завдання №3.
Дослідити функцію  та побудувати її графік.
та побудувати її графік.
1. Дана функція є багаточленом (можна розкрити дужки, отримаємо багаточлен третього ступеня), тому вона визначена, безперервна та диференційована за будь-яких х.
2. Знайдемо похідну.
 .
.
З рівняння у¢ =0 знайдемо критичні точки: 3 х·( х–2)=0, х 1 =0, х 2 =2.
Досліджуємо їх.
х
(–∞, 0)
(0; 2)
(2; +∞)
у ¢
у
3. Отже, функція зростає на інтервалах (–∞, 0) та (2, +∞), зменшується на інтервалі (0; 2), має максимум при х=0 і мінімум при х=2:
у max = у(0)=4; у min = у(2)=0.
4. Знайдемо другу похідну.
у¢¢ = 6·( х-1).
Крива випукла там, де у¢¢ < 0, т. е. 6·(х–1) < 0, х < 1.
Крива увігнута там, де у¢¢ > 0, тобто. х > 1.
Отже, на інтервалі (–∞, 1) крива опукла; а на інтервалі (1, +∞) – увігнута.
5. Точку перегину знайдемо з рівняння у¢¢ =0. Таким чином, х=1 – абсцис точки перегину, т.к. ця точка поділяє інтервали опуклості та увігнутості кривої. Ордината точки перегину: у(1)=2.
Графік функції у=(х+1) · ( х-2) 2 перетинає вісь Ох при у=0, тобто при х= -1 і х=2;
перетинає вісь Оу при х=0, тобто при у=4. Ми отримали три точки: (-1; 0), (2; 0), (0; 4). Усі отримані точки внесемо до таблиці, додавши сусідні із нею.
–2
–1



–16


іс. 4 Крива у=(х+1)(х–2) 2 .
Завдання №1
До вашої уваги пропонуються завдання, в яких можуть бути одна, дві, три та більше правильних відповідей. Обвести кружечком номери всіх правильних відповідей
1. Якщо  то функція
то функція
1) зростаюча
2) спадна
3) постійна
2. Якщо
1) Зростаюча
2) Знижена
3. Якщо  , то функція
, то функція
1) Зростаюча
2) Знижена
4. Якщо  , то функція
, то функція
1) Зростаюча 3) Зменшуюча
2) Постійна 4) Монотонна
5. Функція  Є
Є
1) Парний
2) Не парний
3) ні парної, ні непарної
4) Періодичною
5) Не періодичною
6) Тригонометричної
7) Елементарний
6. Функція  Є
Є
1) парної
2) непарний
3) ні парної, ні непарної
4) періодичний
5) не періодичної
6) тригонометричної
7) елементарною
2) Вейєрштрас 4) Діріхле 6) Лейбніц
8) Рішення  Рівняння
Рівняння
1) 0 3) 0 та 3 5) 2 7) 3
2) 2 та 3 4) 2 6) -5 і 1 8) 5 і 1
9) вирішення нерівності 
1) ( ; 1) 3) (
; 1) 3) ( ; 1) 5) (-
; 1) 5) (- ;1)
;1)
2) (1; 5) 4) (2;  ) 6)
) 6) 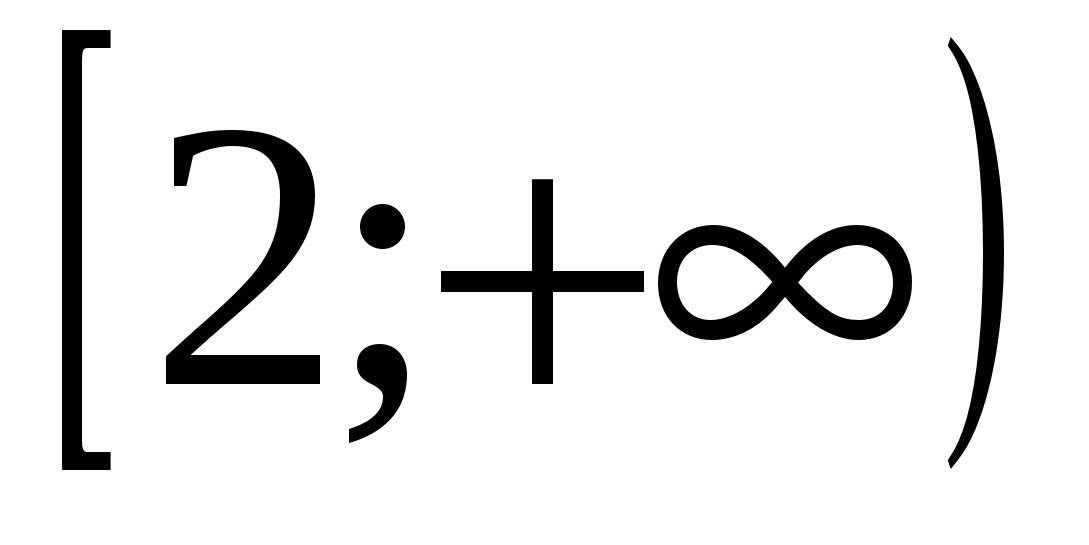
10) Методом  Знаходиться сума
Знаходиться сума
1) векторів
2) прямих
3) відрізка
11) Якщо  , то функція
, то функція
1) Увігнута 3) Випукла 5) Знижена
2) Монотонна 4) Зростаюча 6) Постійна
12) область визначення функції дорівнює 
1) ( ;0)
;0)
2) (0;  )
)
3) (- ;
; )
)
4) (0;1)
5) 
6) 
7) (-1;1)
8) 
9) 
13) функція  є
є
1) показовою
2) тригонометричної
3) статечною
4) логарифмічній
14) якщо функції у = x  то вона є
то вона є 
1) парної
2) непарний
3) ні парної, ні непарної
15) функція  при
при  є
є

 .
.



