العمل التطبيقي
الرياضيات
1. العثور على نهاية الوظيفة. الأول والثاني حدود رائعة.
2. مشتق من وظيفة معقدة. دراسة دالة لمتغير واحد ورسم الرسوم البيانية.
3. اختبار "تطبيق حساب التفاضل والتكامل لدراسة الدوال".
4. إيجاد التكاملات غير المحددة. حساب التكاملات المحددة.
5. حساب المحددات.
6. حل أنظمة المعادلات الخطية باستخدام طريقة كرامر. امتحان.
7. حل المسائل المتعلقة بموضوع "المجموعات". صيغ الجبر المنطقية.
8. حساب احتمالات الأحداث العشوائية. صيغة الاحتمالية الإجمالية.
9. حساب الخصائص العددية.
10. اختبار "أساسيات نظرية الاحتمالات والإحصاء الرياضي"
11. الشكل المثلثي للرقم المركب.
12. الإجراءات ذات الأعداد المركبة بأشكال مختلفة.
تعليمات منهجية للعمل العملي في الرياضيات
الدورة 2
الدرس العملي هو شكل من أشكال تنظيم العملية التعليمية، والذي يتضمن أداء الطلاب لواحد أو أكثر من الأعمال العملية في مهمة وتحت إشراف المعلم.
وهكذا، في الفصول العملية في الرياضيات، يطور الطلاب القدرة على حل المشكلات، والتي يجب استخدامها في المستقبل لحل المشكلات المهنية في التخصصات الخاصة.
في سياق العمل العملي، يتقن الطلاب القدرة على استخدام مصادر المعلومات، والعمل مع الوثائق التنظيمية والمواد التعليمية، والكتب المرجعية، وعمل الرسومات والمخططات والجداول، وحل أنواع مختلفة من المشاكل، وإجراء الحسابات.
المسائل التي يتم حلها أثناء الدروس العملية في الرياضيات:
1) توسيع وتوحيد المعرفة النظرية في الرياضيات المكتسبة خلال المحاضرات؛
2) تطوير المهارات والقدرات العملية لدى الطلاب لحل المشكلات في الرياضيات بنجاح؛
3) تنمية حاجة الطلاب إلى التعليم الذاتي وتحسين المعرفة والمهارات في عملية دراسة الرياضيات؛
4) تشكيل موقف إبداعي ونهج بحثي في عملية دراسة الرياضيات؛
5) تكوين الصفات ذات الأهمية المهنية للمتخصص المستقبلي والمهارات في تطبيق المعرفة المكتسبة في المجال المهني.
الدرس العملي رقم 1.حساب حدود الوظيفة. الأول والثاني حدود رائعة.
موضوع : حساب حدود الوظيفة.
هدف: اكتساب المعرفة الأساسية في مجال الفروع الأساسية للرياضيات . اختبار استيعاب المعرفة حول حساب حدود الوظائف. كرر وتنظيم المعرفة حول هذا الموضوع.
مهام:
تنمية التفكير المهني الإبداعي.
إتقان لغة العلوم، ومهارات مفاهيم التشغيل؛
إتقان مهارات الإعداد وحل المشكلات؛
تعميق التدريب النظري والعملي؛
تنمية المبادرة والاستقلالية لدى الطلاب.
تعزيز مهارات الحوسبة.
مواصلة العمل على الكلام الرياضي.
تكوين مهارات العمل المستقل، والعمل مع الكتاب المدرسي، ومهارات اكتساب المعرفة بشكل مستقل؛
تنمية القدرة على إبراز الشيء الرئيسي عند العمل مع النص؛
تكوين التفكير المستقل، العمليات العقلية: المقارنة، التحليل، التوليف، التعميم، القياس؛
إظهار دور العمل المنهجي للطلاب في تعميق وزيادة قوة المعرفة، حول ثقافة إنجاز المهام؛
تنمية القدرات الإبداعية لدى الطلاب.
تقديم العمل العملي:
المادة النظرية للتوصيات المنهجية للعمل العملي.
الرياضيات, – السلسلة: التعليم المهني الثانوي. - روستوف على نهر الدون "فينيكس"، ص.
تقدم الدرس العملي.
1. صياغة موضوع الدرس، وشرح ارتباط الموضوع بموضوعات التخصص الأكاديمي الأخرى؛
2. التحقق من استعداد الطلاب للفصل.
3. إجراء الدرس الفعلي حسب الموضوع ووفقاً لبرنامج عمل التخصص:
دراسة المادة النظرية حول موضوع "حساب حدود الدوال".
النظر في أمثلة لحل المهام النموذجية.
قم بعمل مستقل على حساب حدود الدوال باستخدام الحدين الملحوظين الأول والثاني.
اجب عن اسئلة الامان.
المعلومات النظرية والتوصيات المنهجية
على حل المشاكل.
1. عرض المواد النظرية.
لحساب نهاية الدالة عند نقطة ما، عليك:
1) عوض بدلاً من المتغير x بما يميل إليه x .
2) إذا حصلنا بعد إكمال الخطوة 1 على عدم يقين في النموذج https://pandia.ru/text/78/405/images/image003_6.png" width="19" height="22 src=">واستبدله السهم مع ناقص: (X-A).
3) إذا تلقينا، بعد إكمال الخطوة 1، حالة عدم يقين من النموذج https://pandia.ru/text/78/405/images/image002_13.png" width="18" height="31 src="> المرتبطة بقيم الدوال المثلثية، يجب علينا استخدام الحد الملحوظ الأول.
تعريف.الحد الأول الملحوظ يسمى الحد
https://pandia.ru/text/78/405/images/image007_4.png" alt="$\displaystyle \lim_(x\to0)\dfrac(\sin x)(x)=1. $" width="102" height="52">!}
5) تعريف:الحد الثاني الرائعيسمى الحد

يلعب الرقم المعطى بواسطة هذا الحد دورًا مهمًا للغاية في التحليل الرياضي وفي فروع الرياضيات الأخرى. الرقم يسمى قاعدة اللوغاريتمات الطبيعية ( https://pandia.ru/text/78/405/images/image009_4.png" alt="$ e$" width="11" height="14">показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:!}
![]()
2. توحيد المواد المدروسة.
مثال 1
https://pandia.ru/text/78/405/images/image015_1.png" width = "28" height = "30 src = ">= -4
استخدمنا القاعدة 1) واستبدلنا بدلاً من x بما يجب أن تسعى إليه x، أي x=2.
مثال 2
https://pandia.ru/text/78/405/images/image017_1.png" width = "154" height = "32 src = ">.png" width = "21" height = "30 src = ">= 5
مثال 3
https://pandia.ru/text/78/405/images/image021_1.png" width = "199" height = "37 src = ">.png" width = "137" height = "35 src = ">. png" width="138" height="24 src=">=3+3=6
مثال 4
https://pandia.ru/text/78/405/images/image004_7.png" width = "22" height = "31 src = ">.png" width = "104" height = "46 src = ">. png" الارتفاع = "30 src = ">
مثال 5
https://pandia.ru/text/78/405/images/image032_0.png" width = "61" height = "46 src = ">.png" height = "30 src = "> = 2
مثال 6
https://pandia.ru/text/78/405/images/image036_0.png" width = "18" height = "28 src = ">
ب) 
الخامس) 
3. توحيد المعرفة والمهارات والقدرات.
القيام بعمل مستقل لحساب حدود الوظائف.
العمل العملي رقم 1. الخيار 1 احسب نهاية الدالة: 1. 2. 3. 10. | العمل العملي رقم 1. الخيار 2 احسب نهاية الدالة: 1. 2. 3. 10. |
العمل العملي رقم 2.
موضوع : العثور على مشتقة وظيفة. دراسة دالة لمتغير واحد ورسم رسم بياني.
هدف : اختبار عملي لمعرفة مفهوم مشتقة دالة، القدرة على إيجاد مشتقات الدوال الأولية، الدوال المعقدة، الدوال العكسية، استخدام جدول المشتقات وقواعد التفاضل، مفهوم الدالة المركبة والعكسية، القدرة لاستخدام مشتق لدراسة الوظائف.
توفير العمل العملي:
كتاب مدرسي. "الرياضيات". - م: حبارى، 2010.
الرياضيات. م: منتدى إنفا 2008.
بطاقات فردية مع خيار العمل العملي.
1. المواد النظرية والأمثلة لإيجاد مشتقة الدالة.
تعريف:مشتق الدالة f(x) (f"(x)) عند النقطة x هو حد نسبة زيادة الدالة إلى زيادة الوسيطة عندما تميل زيادة الوسيطة إلى الصفر:
https://pandia.ru/text/78/405/images/image061_0.png" width="209 height=235" height="235">
قواعد التمايز.
إذا كانت الدالتان f(x) وg(x) لهما مشتقات، إذن
2. (u+v)′=u′+v′
3. (uv)′=u′v+v′u
4. (C u)′=C u′، حيث C=const
5..png" width="49" height="54 src=">
6. مشتق من وظيفة معقدة:
و'(ز(س))=و'(ز) ز'(س)
2. أمثلة.
1..png" العرض = "61" الارتفاع = "41 src = ">.png" العرض = "20" الارتفاع = "41 src = ">.png" العرض = "20" الارتفاع = "41 src = "> .png" width="69" height="41 src=">+4).
الدالة هي نتاج عاملين: u=https://pandia.ru/text/78/405/images/image071_0.png" width="72" height="41 src=">.png" width=" 64" الارتفاع = "41 src = ">.png" العرض = "19" الارتفاع = "41 src = ">.png" العرض = "45" الارتفاع = "51 src = ">.
الدالة هي حاصل تعبيرين: u=https://pandia.ru/text/78/405/images/image079.png" width="52" height="41 src=">..png" width= "215" " الارتفاع = "57 src = ">.png" العرض = "197 الارتفاع = 36" الارتفاع = "36">
حل. لنجد مشتق هذه الوظيفة باستخدام قاعدة التمايز بين الوظائف المعقدة (الصيغة 6):

5. إذاً 
6. ذ = س 3 – 3س 2 + 5س+ 2. دعونا نجد ذ "(–1).
ذ " = 3س 2 – 6س+ 5. لذلك، ذ "(–1) = 14.
7. لو ذ= سجل سكوس س، الذي - التي ذ" = (ل س)"كوس س+ln س(كوس س) " =1/س∙كوس س-ln سخطيئة س.
دع الوظيفة تعطى. لدراستها تحتاج:
1) ابحث عن مجال تعريفه. إذا لم يكن الأمر صعبًا للغاية، فمن المفيد العثور على النطاق أيضًا. (ومع ذلك، في كثير من الحالات، يتم تأجيل مسألة العثور حتى يتم العثور على الحدود القصوى للدالة.)
2) تعرف على الخصائص العامة للدالة التي ستساعد في تحديد سلوكها: هل الدالة زوجية أم فردية، هل هي دورية.
3) اكتشف كيف تتصرف الدالة عندما تقترب الوسيطة من النقاط الحدودية لمجال التعريف، إذا كانت هناك نقاط حدودية من هذا القبيل. إذا كانت الدالة تحتوي على نقاط انقطاع، فيجب أيضًا التحقق من هذه النقاط للتأكد من وجود خطوط مقاربة رأسية للدالة. ابحث عن الخطوط المقاربة المائلة.
4) ابحث عن نقاط تقاطع الرسم البياني مع محاور الإحداثيات، والتي تتكون ببساطة من حساب قيمة الدالة تحت الشرط:
مع محور OX: y=0;
مع محور OY: x=0.
إن العثور على نقاط التقاطع مع المحور قد يؤدي إلى الحاجة إلى حل معادلة جبرية معقدة، والتي ربما لا يمكن حلها إلا بشكل تقريبي. بعد إيجاد جذور الدالة ونقاط الاتصال، يمكننا تحديد إشارة الدالة عند كل فترة من الفترات بين هذه النقاط. يمكن القيام بذلك إما عن طريق حساب قيمة الدالة عند أي نقطة في الفترة، أو باستخدام طريقة الفترة.
5) البحث عن فترات الرتابة. للقيام بذلك، أوجد المشتقة وحل المتراجحة:
https://pandia.ru/text/78/405/images/image089.png" width = "49" height = "19 src = ">، الوظيفة تتناقص.
بعد العثور على فترات الرتابة، يمكننا على الفور تحديد نقاط الحد الأقصى المحلي: حيث يتم استبدال الزيادة بانخفاض، وتقع الحدود القصوى المحلية، وحيث يتم استبدال النقصان بزيادة، وتقع الحدود الدنيا المحلية.
6) يتم إيجاد فترات التحدب والتقعر باستخدام المشتق الثاني..png" width="39" height="19 src="> على الفترات:
إذا كان https://pandia.ru/text/78/405/images/image090.png" width="39" height="19 src=">‹0، فإن منحنى الرسم البياني للوظيفة يكون محدبًا.
في الوقت نفسه، نحدد نقاط الانعطاف على أنها تلك النقاط التي تغير فيها الدالة اتجاه التحدب (وتكون مستمرة).
7) إيجاد نقاط تقاطع الرسم البياني مع الخط المقارب والنقاط الإضافية. هذه النقطة ليست إلزامية، ولكن العثور على مثل هذه النقاط يجعل دراسة الدالة ورسمها البياني كاملة وكاملة.
لاحظ أنه من المفيد رسم النقاط على محاور الإحداثيات وعلى الرسم البياني الذي تم الحصول عليه أثناء دراسة الوظائف على الرسم على الفور. وهذا يساعد على فهم مظهر الرسم البياني على طول الطريق.
3. افعل ذلك بنفسك:
|
خيار | أوجد مشتقة الدالة y: |
خيار | أوجد مشتقة الدالة y: |
1.ص=6- | 1. ص=-6- 5.ص= |
||
1. ص=-7-1 | 1. ص=-7-1 |
||
1.y=4x-3tgx+6x-8 | 1.y=-5x+2ctgx+3x-2 |
||
أهداف الدرس:
التعليمية- معرفة صيغ التمايز. قواعد التمايز.
التمييز بين وظيفة معقدة. المعنى الفيزيائي والهندسي للمشتق؛
معادلة المماس للرسم البياني للدالة.
التنموية -تكون قادرة على العثور على مشتقات الوظائف. حل المشكلات باستخدام المعنى المادي، والمعنى الهندسي؛ أوجد قيمة مشتقة دالة عند نقطة ما؛ شرح وتبرير الإجراءات التي تم تنفيذها بشكل صحيح رياضيا.
تعليمية –زراعة الاستقلال والمسؤولية والتفكير.
خلال الفصول الدراسية
I. اللحظة التنظيمية.
ثانيا. التحقق من الواجبات المنزلية
(خلال فترات الاستراحة، يقوم المستشارون بفحص (الطلاب) وتحديد الدرجات).
ثالثا. تحديد الأهداف والتحفيز
يعلم المعلم الطلاب أن هذا الدرس هو الدرس الأخير في موضوع "حساب المشتقات" ويدعوهم إلى صياغة أهدافهم الخاصة.
المعلم: “قال الفيلسوف العظيم كونفوشيوس ذات مرة: “ثلاثة طرق تؤدي إلى المعرفة: طريق التفكير هو أنبل الطرق، وطريق التقليد هو أسهل الطرق، وطريق التجربة هو أكثر الطرق مرارة.” لذلك، اليوم في الفصل، سيحدد كل واحد منكم المسار الذي يسلكه لمعرفة هذا الموضوع.
يتم تكليف الطلاب بمهمة إظهار معرفتهم ومهاراتهم في حساب المشتقات ويتم إعطاؤهم خطة درس.
المرحلة الأولى:إكمال المهمة باستخدام بطاقة "التذكر".
(اختبار معرفة الصيغ وقواعد التفاضل).
المرحلة الثانية:العمل الجبهي الشفهي على التكرار وتعميم المعرفة.
المرحلة الثالثة:"توقعات الاختبار" (عند تنفيذ هذه المهمة، تكون مساعدة الاستشاريين مقبولة).
أناالمرحلة الخامسة:حل مشكلة عملية.
المرحلة الخامسة:عمل مستقل
يتم تقييم المراحل الأولى والثالثة والخامسة من العمل والواجبات المنزلية. يقوم الاستشاريون بفحص النتائج وإدخالها في جدول التقييم.
معيار التقييم: "5"- 19-20 نقطة؛
"4"- 15-18 نقطة؛
"3"- 10-14 نقطة.
مسارات إلى المعرفة
- الاستنساخ وتصحيح المعرفة المرجعية
المرحلة الأولى.
هدف:السيطرة والتحكم الذاتي في معرفة الصيغ وقواعد التمايز
يتذكر! إف آي. _______________________________________ |
|
المشتق |
|
ج، ج - سلبيات ر |
|
|
|
|
|
F"(خ)+ ز"(خ) |
|
F(خ)* ز(خ) |
|
|
|
في نهاية هذه المهمة، يتم إجراء اختبار ذاتي باستخدام "جدول المشتقات". يتم تسليم البطاقات إلى الاستشاريين للتحقق منها (لا يُسمح بالتصحيحات على البطاقات).
خامسا: تعميم وتنظيم المعرفة
المرحلة الثانية.
1. العمل الجبهي عن طريق الفم.
أ.إنشاء مهمة لهذا الشرط وحلها.
![]()
1. أوجد قيمة مشتقة الدالة عند النقطة t = 3. (الجواب: 21.)
2. أنشئ معادلة لمماس الرسم البياني للدالة عند النقطة t = 3. (الإجابة: y = 21x-45.).
3. أوجد سرعة الجسم وتسارعه في اللحظة t=3c، إذا كان قانون الحركة معطاة بالصيغة. (الإجابة: 21 م/ث، 16 م/ث²).
4. أوجد المعامل الزاوي للمماس المرسوم على الرسم البياني للدالة عند النقطة t = 3. (الإجابة: 21.).
5. أوجد ظل زاوية ميل المماس للرسم البياني للدالة عند النقطة t = 3 وحدد نوع الزاوية بين المماس والاتجاه الموجب لمحور الثور. (الإجابة: tgα، الزاوية α حادة)
ب. إيجاد مشتقات الدوال

2. المرحلة الثالثة"توقعات الاختبار"


وفي نهاية هذه المهمة يتم إجراء اختبار ذاتي بناءً على الإجابات النهائية وتسليم الاختبارات إلى الاستشاريين. (التصحيحات على البطاقات غير مسموح بها).
الإجابات:
1 خيار |
||||
الخيار 2 |
- حل المشكلة
أناالمرحلة الخامسة
حل أمامي لمشكلة ذات مستوى متقدم (يتم تنفيذ الحل بواسطة استشاريين مع الفصل).
مهمة
في ما قيم المعلمة أالظلال على الرسم البياني للوظيفة ![]()
المرسومة عند نقاط تقاطعها مع المحور X تشكل زاوية قياسها 60° فيما بينها؟

الرسم البياني عبارة عن قطع مكافئ مع فروع تصاعدية تتقاطع مع المحور X عند نقطتين (الحالة أ=0 لا يفي بمعنى المشكلة):
تاسعا. التلخيص والتصنيف
1. الأسئلة: أ) هل تم تحقيق الغرض من الدرس؟
ب) ما هي المرحلة التي بدت الأكثر صعوبة؟
ج) ما هو الأكثر إثارة للاهتمام؟
2. يعلن الاستشاريون النتائج (عدد وأسماء الطلاب في الطريق
التقليد وطرق التأمل وطرق التجربة).
درس عملي
موضوع:إيجاد المشتقات. تطبيق المشتق لدراسة الوظائف ورسم الرسوم البيانية.
هدف: إتقان حساب المشتقات، وتعلم استكشاف دالة باستخدام المشتقة
وسائل التعليم:دفاتر ملاحظات للتمارين العملية وعروض تقديمية حول الموضوع وموارد الإنترنت.
1. النظر في المواد النظرية حول المواضيع: "قواعد حساب المشتقات"، "أقصى الدالة"، "التحدب، التقعر". نقطة الأنحراف."
2. مراجعة نماذج من الواجبات.
3. أكمل مهمة الاختبار رقم 1.
أسئلة التحكم:
1. تحديد الحد الأقصى (الحد الأدنى) للدالة عند نقطة ما. ماذا يمكن أن يقال عن علامة زيادة الوظيفة في حي صغير إلى حد ما من النقطة القصوى (الدنيا)؟
2. ما هي الشروط اللازمة لوجود الحد الأقصى للدالة؟ ما هو معناها الهندسي؟
3. ما هي قاعدة العثور على أكبر وأصغر قيم للدالة على القطعة؟
4. تعريف التحدب (التقعر) للمنحنى على فترة.
5. ما هي قاعدة إيجاد فترات التحدب وتقعر المنحنى؟
6. نقطة انعطاف المنحنى. كيف تجدها؟
7. ما هي الخوارزمية لإنشاء رسم بياني للدالة؟
قواعد لحساب المشتقات
مشتق من وظيفة معقدة.
لو في=ƒ( و), ش=φ(خ) إذن في¢ ( X)=ƒ¢ (ط)·φ¢ (X).
مشتق من المبلغ.
لو في(X)=و(X)+الخامس (X)، الذي - التي في¢ (X)=و¢ (X)+الخامس ¢ (X)
مشتق من المنتج.
لو ذ(س)=ش(X)· الخامس (X)، الذي - التي في¢ = و¢ · الخامس + ش · الخامس ¢ .
بخاصة، ( مع· و)¢ =ج· و¢، أي يتم إخراج العامل الثابت من تحت علامة المشتقة. ومن السهل التحقق من ذلك
(ش 2 ) ¢ = 2 ش·ش ¢ ، (ش 3 ) ¢ =3u 2 ش ¢ ، ... ، (ش ن ) ¢ =ن·ش ن-1 ش ¢ .
مشتق من الحاصل.
اذا ثم  .
.
جدول المشتقات
1. (مع)¢ =0
لوظيفة معقدة: إذا ش = ش (س)، الذي - التي:
2. (X)¢ =1
3. (x α )¢ = α · Xα-1، أ- أي عدد حقيقي.
 .
.
3. 

4. (أ X ) ¢ =أ X · ln أ
4. 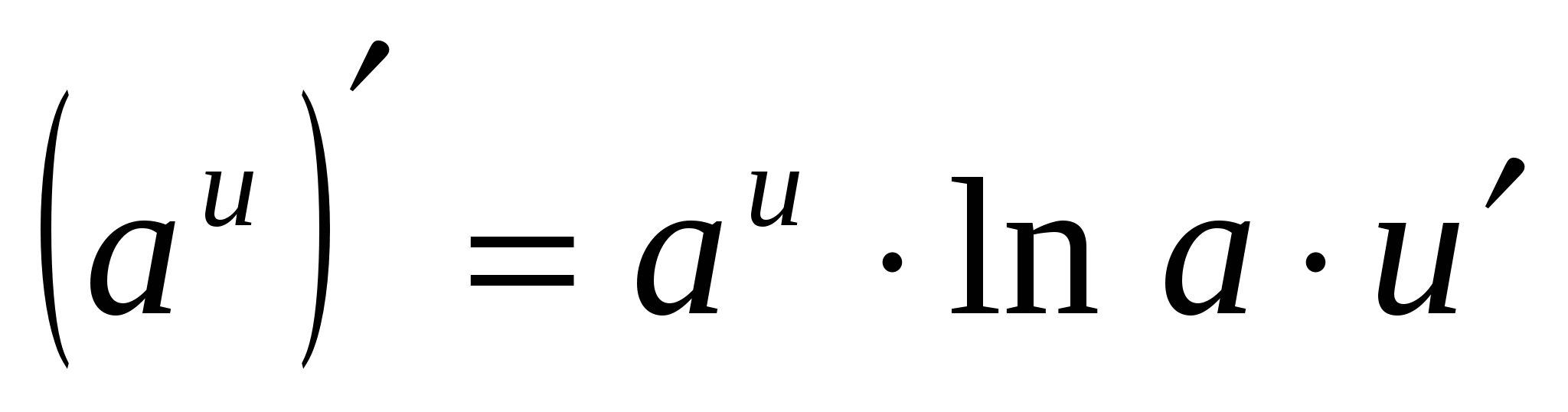

5. (سجل
أ
س)
¢
=
 .
.
5. 

6. (الخطيئة س)¢ = جتا س
6. 
7. (كوس س)¢ = -الخطيئة س
7. 
8. (تيراغرام س)¢
=
8. 
9. (ctgx)¢
=
9. 
10. 
10. 
11. 
11. 
12. 
12. 
13. 
13. 
مراجعة الأمثلة
مثال 1.
ص=(3-2 خطيئة 5x ) 4 | نحن نطبق الصيغ المشتقة ل و α ,الخطيئة ش |
ذ ¢ =4·(3–2·الخطيئة5x) 3·(3–2الخطيئة5x) ¢ =4·(3–2·الخطيئة5x) 3 ·(0–2·cos5x·5) = -40·(3–2·sin5x) 3 .
مثال 2.
. 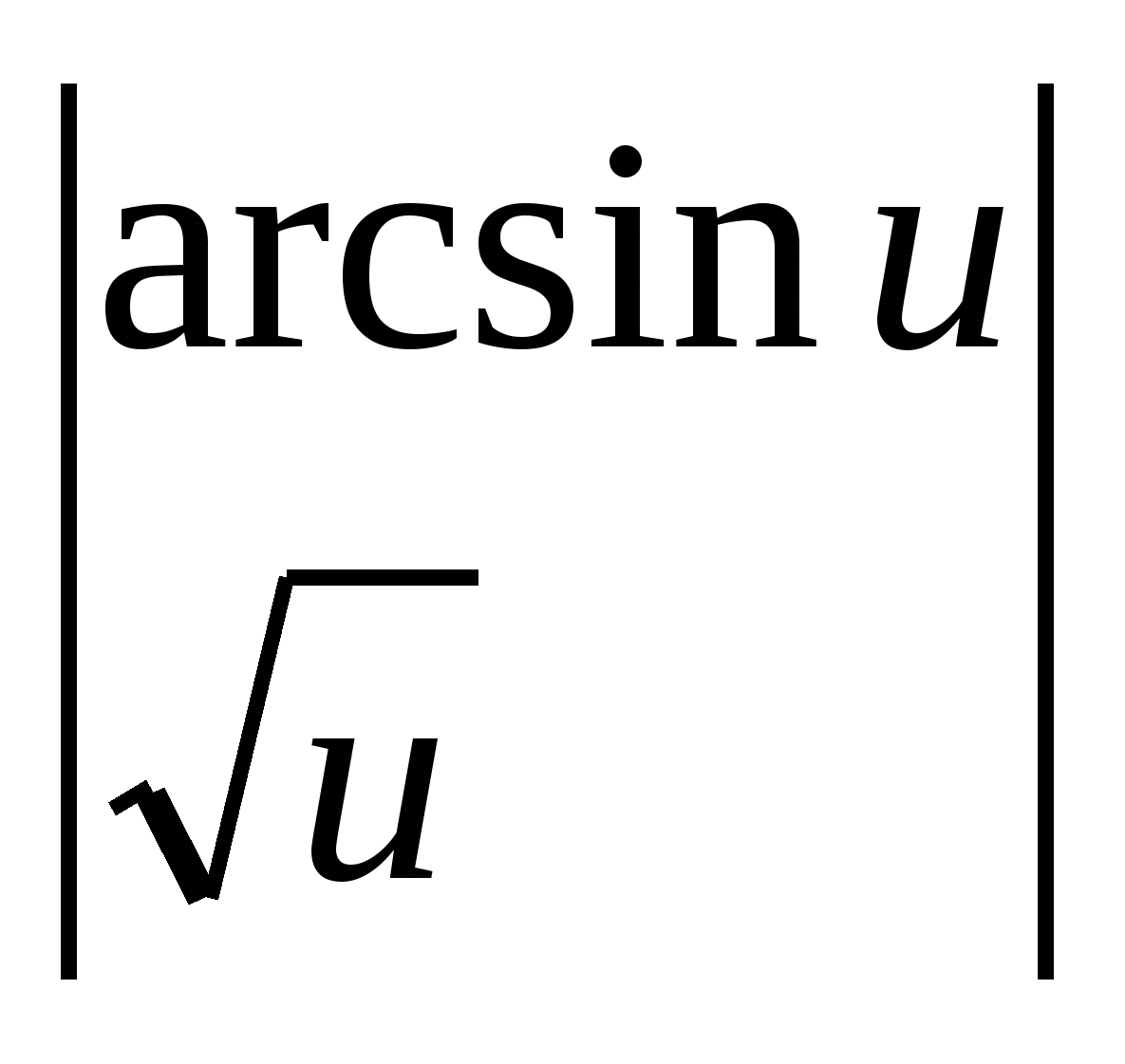

مثال 3.
 .
. 

مثال 4.



مثال 5.
 .
. 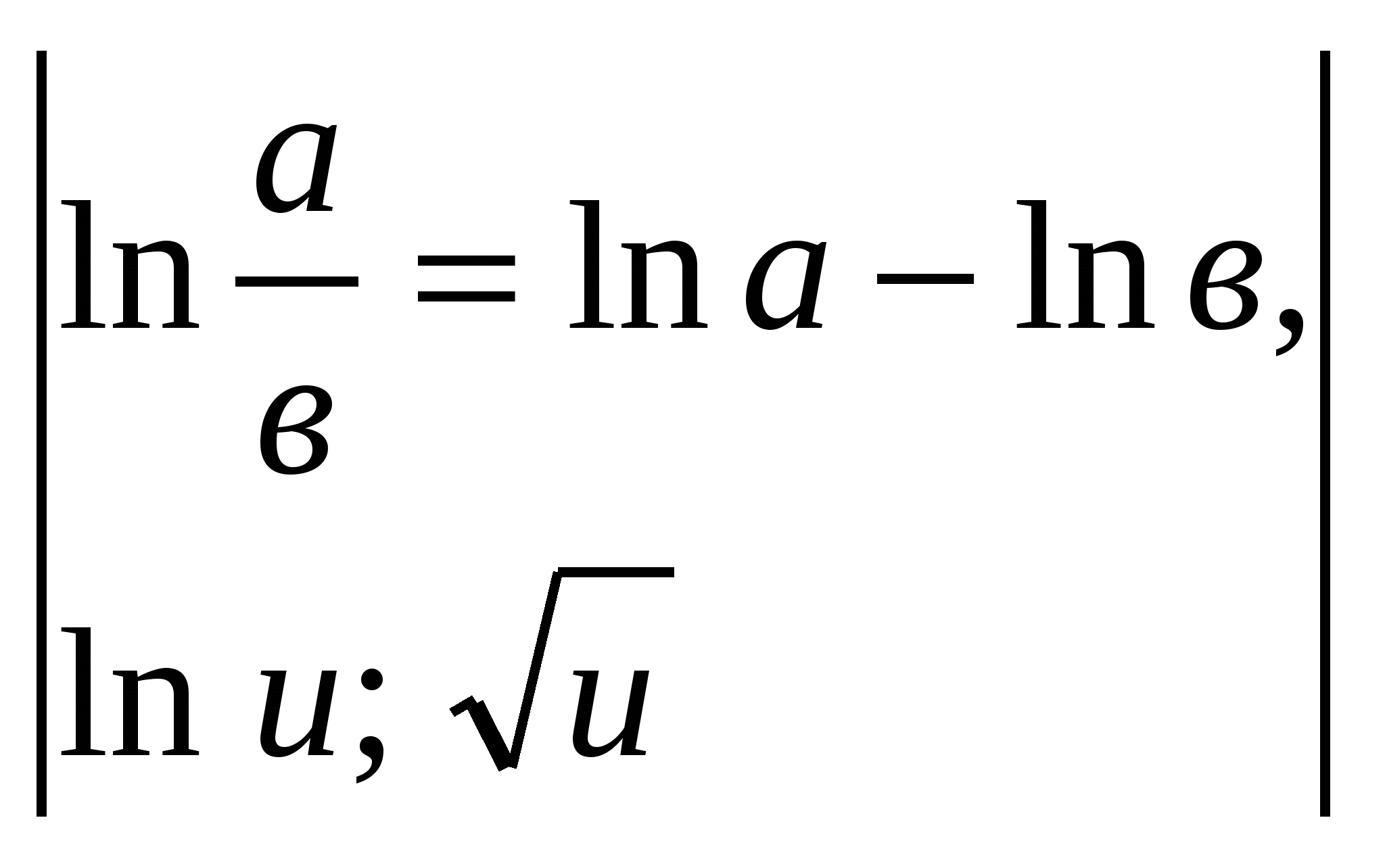

الحد الأقصى للوظيفة
تعد دراسة الدالة عند الحد الأقصى أحد أهم تطبيقات المشتقات. دعونا نلقي نظرة على تعريف الحد الأدنى والحد الأقصى وكيفية العثور عليهما.
دع الدالة ƒ( X) يتم تعريفها وتمييزها على مجموعة معينة ونقطة معينة X 0 نقطة بداخله.
تعريف.وظيفة ƒ (X) عند نقطة X 0 لديه أقصى(الحد الأدنى)، إذا كان هناك مثل هذا الحي للنقطة X 0، وهو للجميع Xمن هذه المنطقة ƒ (X) < ƒ (X 0 ) (ƒ (X) > ƒ (X 0 )).
نقطة Xثم يسمى 0 نقطة أقصى(الحد الأدنى).

أرز. 1.
يظهر رسم بياني لدالة لها نقطتان كحد أقصى ( X 1 و X 3) ونقطتين كحد أدنى ( X 2 و X 4)، وقد تكون القيمة القصوى أقل من الحد الأدنى ( ƒ (X 1 ) < ƒ (X 4)). وهذا يؤكد حقيقة أننا نميز تفرد الوظيفة فقط بالقرب من نقطة معينة.
تسمى قيم الوظيفة عند نقاط الحد الأقصى والأدنى بالقيم المتطرفة أو التطرف. الرسم البياني أعلاه يوضح أن النقاط القصوى ( X 1 , X 2 , X 3 , X 4) تحديد فترات رتابة الوظيفة، في كل منها يحتفظ المشتق بعلامة معينة. عند النقاط القصوى، بالطبع، تصل المشتقة إلى الصفر. دعونا صياغة نظرية حول شرط ضروري وجود الحد الأقصى.
نظرية.إذا كانت الوظيفة ƒ (X) عند نقطة X 0 له حد أقصى، فإن مشتقة الدالة عند هذه النقطة تساوي الصفر، أي ƒ ( X 0)=0.
ولنلاحظ على الفور أن هذا الشرط غير كاف، أي أن العبارة العكسية ليست صحيحة دائمًا. من المساواة ƒ ¢ ( X 0)= 0 لا يتبع ذلك بالضرورة عند هذه النقطة X 0 هناك حد أقصى.
يتم تأكيد ذلك من خلال مثال مع الوظيفة ƒ (X)=س 3 .
سوف نجد ƒ ¢ ( X)= 3X 2 . عند هذه النقطة X=0 ƒ ¢ (0)=0 . ولكن أقرب إلى هذه النقطة كما تريد X=0 سوف نجد X> 0، حيث ƒ (X)=س 3 > 0, سوف نجد X< 0, где ¦ (X)=X 3 < 0. Т. е. не существует какая-либо малая окрестность точки X=0، حيث للجميع Xقيمة الدالة عند نقطة ما X=0 سيكون الأكبر أو الأصغر. ولذلك نقطة X=0 ليست نقطة متطرفة.
يمكن للمرء أن يجادل بشكل مختلف. منذ المشتقة ƒ ¢ (س)=3س 2 ، ثم الدالة ƒ(س)=س 3 يزيد لأي x حقيقي وليس له حدود قصوى.
النقاط التي يتم عندها استيفاء الشرط الأقصى الضروري (ƒ ¢ (س)=0)وتسمى شديد الأهمية .
من الواضح أن مماس الرسم البياني للدالة عند النقاط حيث ƒ ¢ (س)=0،بالتوازي مع المحور السيني الثور .
شرط كافويرد الحد الأقصى في النظريات التالية.
النظرية 1.لو X 0 هي النقطة الحرجة للدالة وعند المرور عبرها تظهر علامة التغييرات المشتقة X 0 هي نقطة قصوى، أي إذا تغيرت إشارة المشتقة من موجب إلى ناقص، فهي نقطة عظمى، وإذا تغيرت إشارة من ناقص إلى موجب، فهي نقطة صغرى.
لاحظ أنه لا يوجد حد أقصى عند نقطة ما إذا لم تتغير إشارة المشتقة. وقاعدة دراسة الحد الأقصى باستخدام المشتق الأول معروفة من المقرر الدراسي. في بعض الأحيان يكون من الملائم أكثر صياغة شرط كافٍ للحد الأقصى باستخدام المشتق الثاني.
دع الدالة ƒ( X) قابل للتمييز مرتين في بعض المجالات (أي ƒ( X) لديه ƒ ( X) و ƒ ¢¢ ( X)).
النظرية 2.لو X 0 - النقطة الحرجة للوظيفة ƒ(خ)و ƒ ¢¢ (x 0 ) > 0 ، الذي - التي X 0 - الحد الأدنى للنقطة إذا ƒ ¢¢ (x 0 ) < 0, то X 0 - النقطة القصوى.
باستخدام المشتق الثاني، يتم تحديد تحدب أو تقعر الرسم البياني للدالة.
التحدب، التقعر. نقطة الأنحراف.
منحنى ص=ƒ(X) يسمى بشكل محدبذ أقلأي منها الظل
ƒ ¢¢ ( X) < 0.
منحنى ص=ƒ(X) يسمى مقعر على فترة إذا كانت جميع نقاط المنحنى تقع أعلى أي منها الظل في هذه الفترة. ثم في هذه الفترة
ƒ ™ ™ (خ) > 0
تعريف. نقطة الأنحراف المنحنى هو النقطة التي يكون فيها المنحنى محدبًا من جهة ومقعرًا من جهة أخرى.
عند نقطة الانعطاف ƒ ¢¢ ( X)=0.
لذلك، فإن علامة المشتق الثاني (وكذلك علامة الدالة نفسها ومشتقها الأول) تشير إلى ميزات الرسم البياني للدالة. دعونا ننظر إليهم مرة أخرى.
إذا للجميع Xفي الفاصل ( أ, ب) ƒ (X) > 0 (ƒ (X) < 0)، ثم يقع الرسم البياني أعلى (أسفل) المحور السيني.
إذا للجميع Xفي الفاصل ( أ, ب) ƒ ¢ ( X) > 0 (ƒ ¢ ( X) < 0), то функция на (أ, ب) يزيد (ينقص).
إذا للجميع Xفي الفاصل ( أ, ب) ƒ ¢¢ ( X) > 0 (ƒ ¢¢ ( X) < 0), то график на (أ, ب) محدبة مقعرة).
المعادلة ƒ( X)=0 يحدد "أصفار" الدالة، أي نقاط تقاطع الرسم البياني مع محور الثور.
المعادلة ƒ ¢ ( X)=0 يحدد النقاط الحرجة.
المعادلة ƒ ¢¢ ( X)=0 يحدد نقاط انعطاف محتملة.
مخطط دراسة الوظيفة
لدراسة الدالة ƒ (X) والتآمر ص=ƒ(X) ينبغي العثور على:
1) مجال تعريف الوظيفة ونقطة تقاطع الرسم البياني مع محاور الإحداثيات؛
2) فترات الرتابة.
3) النقاط القصوى وقيم الدالة عند هذه النقاط؛
4) فترات التحدب وتقعر الرسم البياني.
5) نقاط انعطاف الرسم البياني.
6) إنشاء جميع النقاط التي تم الحصول عليها في نظام الإحداثيات الديكارتية (أحيانًا يتم الحصول على نقاط إضافية لتوضيح الرسم البياني) والرسم البياني نفسه.
أصغر وأكبر قيم الدالة على القطعة
عند حل بعض مشاكل طريقة التحسين، من المهم أن تكون قادرًا على العثور على أصغر أو أكبر قيم للدالة في جزء معين. تصل الدالة إلى هذه القيم إما في النقاط الحرجة أو في نهايات المقطع.
مخطط البحثأصغر وأكبر قيم الدالة ƒ (X) على الجزء [ أ, ب].
1. أوجد مشتقة الدالة ƒ ¢ ( X).
2. أوجد النقاط الحرجة من المعادلة ƒ ¢ ( X)=0.
3. حدد تلك النقاط الحرجة التي تنتمي إلى هذا الجزء [ أ, ب] وأوجد قيمة الدالة ƒ (X) في كل نقطة من هذا القبيل.
4. حساب قيم الوظائف ƒ (X) في نهاية المقطع: ƒ( أ) و ƒ( ب).
5. من قيم الوظائف التي تم الحصول عليها، حدد الأكبر (الأكبر) والأصغر (الأصغر).
مثال 2.
العثور على أكبر وأصغر قيم للدالة ƒ(خ)=X 3 -9x 2 +24x-10على الجزء.
1. ƒ ¢ ( X)= 3X 2 – 9·2 X 2 + 24.
2. ƒ ¢ ( X)=0, 3(X 2 –6X+8)=0, X 1 =2, X 2 =4.
3. النقطة × 2 = 4 لا تنتمي إلى القطعة. ولذلك، فإننا نحسب قيمة الدالة عند النقطة فقط X 1 =2
ƒ(2)=2 3 –9·2 2 +24·2–10=10.
4. قيم الدالة في نهايات المقطع: ƒ(0)= –10, ƒ(3)=3 3 –9·3 2 +24·3–10, ƒ(3)=8.
5. القيم التي تم الحصول عليها:
ƒ(2)=10، ƒ(0)= –10، ƒ(3)=8.
أعلى قيمة هي 10 ويتم الوصول إليها عند هذه النقطة X=2. الأصغر يساوي -10 ويتحقق عند هذه النقطة X=0.
مثال 3.
أوجد فترات التحدب والتقعر ونقاط انعطاف المنحنى ص=س+36X 2 –2X 3 –X 4 .
مجال تعريف هذه الدالة هو مجموعة جميع الأعداد الحقيقية، أي. XЄ(–∞, +∞).
دعونا نجد المشتق الثاني.
في¢ = 1+72 X–6X 2 –4X 3 .
في¢ ¢ = 72-12 X–12X 2 = –12(X 2 +X–6).
من مكافئ. في¢ ¢ = 0 نحصل على الإحداثي الإحداثي لنقطة الانعطاف:
–12(X 2 +X–6)=0 X 1 = –3; X 2 =2.
دعونا نحدد العلامة في™ على فترات
(–∞; –3), (–3; 2), (2, +∞).
X
(–∞, –3)
(–3; 2)
(2; +∞)
في¢¢
شكل منحنى
محدب
انثناء
مقعر
انثناء
محدب
لنجد إحداثيات نقاط الانعطاف:
في(–3)=726; م 1 (–3; 726) – نقطة انعطاف
في(2)=114; م 2 (2; 114) – نقطة انعطاف.
في الفترة (-3؛ 2) يكون المنحنى مقعرًا. على الفترات (–∞; –3) و (2; +∞) – محدبة.
عينات من المهام
المهمة رقم 1.
أوجد نقاط توقف الدالة ورسم الرسم البياني

وظيفة ƒ (X) يتم تعريفه لجميع الحقيقي Xومستمر في كل من الفترات المشار إليها: (–∞; –1), [–1; 0]، (0، +∞). دعونا استكشاف الوظيفة ƒ (X) للاستمرارية عند النقاط X= -1 و X=0.
للقيام بذلك، سنجد حدودًا من جانب واحد عند كل نقطة من هذه النقاط.

وبما أن الحدود من جانب واحد مختلفة، إذن X = –1 – نقطة الانقطاع من النوع الأول.

الحدود من جانب واحد متساوية، أي عند النقطة x=0 هناك نهاية للدالة و 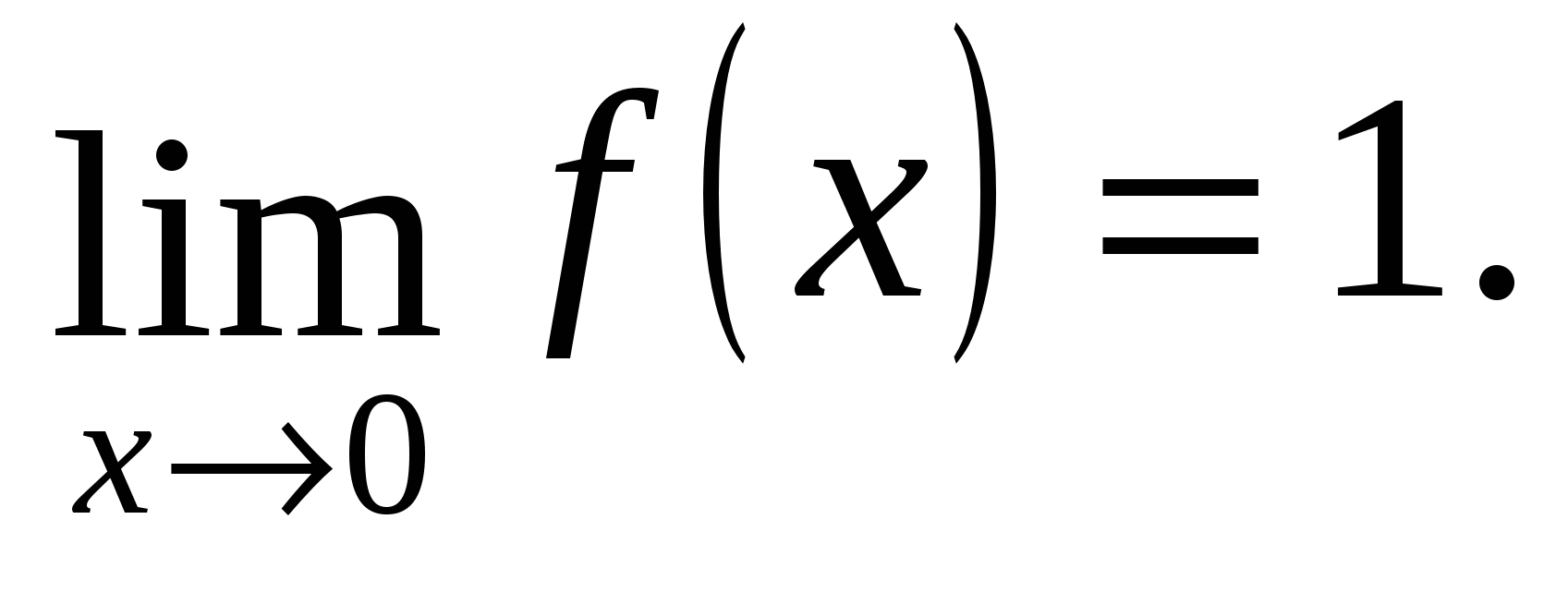
دعونا نقارن هذا الحد بقيمة الدالة عند النقطة: 
لأن  ثم في عند x=0 تكون الدالة ƒ(x) مستمرة.
ثم في عند x=0 تكون الدالة ƒ(x) مستمرة.
لنرسم الدالة ƒ (X)، بشرط
1)  - معادلة الخط المستقيم،
- معادلة الخط المستقيم،
2)  - معادلة نصف الدائرة العلوية
- معادلة نصف الدائرة العلوية  مع مركز عند نقطة الأصل ونصف قطر يساوي الوحدة، وتحت الشرط -1 جنيه استرليني Xمعادلة 0 جنيه استرليني
مع مركز عند نقطة الأصل ونصف قطر يساوي الوحدة، وتحت الشرط -1 جنيه استرليني Xمعادلة 0 جنيه استرليني  يحدد ربع الدائرة.
يحدد ربع الدائرة.
3) ل X > 0 يتم إعطاء الرسم البياني بالمعادلة  . نجد نقاط تقاطع هذا المنحنى مع محور الثور من المعادلة
. نجد نقاط تقاطع هذا المنحنى مع محور الثور من المعادلة  لـ x > 0.x= π
ن، أين ن
=1, 2, 3, 4,
لـ x > 0.x= π
ن، أين ن
=1, 2, 3, 4,

أرز. 2.
المهمة رقم 2.
اكتب معادلات مماسات الخط  في نقاط حيث X=0 و X=4. أوجد نقطة تقاطع المماسين والزاوية بينهما. جعل الرسم.
في نقاط حيث X=0 و X=4. أوجد نقطة تقاطع المماسين والزاوية بينهما. جعل الرسم.
معادلة المماس للخط ص=ƒ(س)يشبه
أين في 0 =ƒ( X 0).
عند هذه النقطة X=0 في(0)=ƒ(0)=5.
في¢ =ƒ ¢ (X)=X-3 ƒ (0)= -3.
م 1 (0، 5) له النموذج ذ- 5= –3(X-0) أو
ص= –3X+5.
عند هذه النقطة X=4 في(4)=ƒ(4)=1. ƒ (4)=4–3=1.
معادلة المماس عند نقطة ما م 2 (4، 1) لديه النموذج ذ- 1=X-4 أو
ص=س–3.
نحصل على نقطة تقاطع الظلال عن طريق حل النظام

نقطة التقاطع م 3 (2, –1).
ركن φ بين الظلال نجد من الصيغة:
 ,
,
أين ك 1 = –3; ك 2 =1 - المعاملات الزاوية للظلال.
 .
.
ركن φ = القطب الشمالي 2.
دعونا نبني هذا الخط  - قطع مكافئ ذو قمة عند النقطة التي X=3، لأن في¢
=0 في X=3. سوف نجد
- قطع مكافئ ذو قمة عند النقطة التي X=3، لأن في¢
=0 في X=3. سوف نجد  . نقطة م 4 (3;
. نقطة م 4 (3;  ) هو رأس القطع المكافئ.
) هو رأس القطع المكافئ.
ر 
يكون. 3.
المهمة رقم 3.
استكشاف الوظيفة  ورسمها.
ورسمها.
1. هذه الدالة هي كثيرة الحدود (يمكنك فتح الأقواس، نحصل على كثيرة الحدود من الدرجة الثالثة)، وبالتالي فهي محددة ومستمرة وقابلة للاشتقاق لأي X.
2. دعونا نجد المشتقة.
 .
.
من مكافئ. في¢ =0 لنجد النقاط الحرجة: 3 X·( X–2)=0, X 1 =0, X 2 =2.
دعونا نستكشفهم.
X
(–∞, 0)
(0; 2)
(2; +∞)
في ¢
في
3. إذن، تزداد الدالة على الفترات (–∞، 0) و (2، +∞)، وتتناقص على الفترة (0؛ 2)، ولها قيمة عظمى عند x=0 وحد أدنى عند x=2:
في الحد الأقصى = في(0)=4; فيدقيقة = في(2)=0.
4. دعونا نجد المشتقة الثانية.
في¢¢ = 6·( X-1).
المنحنى محدب حيث في¢¢ < 0, т. е. 6·(X–1) < 0, X < 1.
المنحنى مقعر حيث في¢¢ > 0، أي X > 1.
إذن، في الفترة (-∞، 1) يكون المنحنى محدبًا؛ وعلى الفترة (1، +∞) تكون مقعرة.
5. نجد نقطة الانقلاب من المعادلة في¢¢ =0. هكذا، X=1 - نقطة الانعطاف، لأن تفصل هذه النقطة بين فترات التحدب وتقعر المنحنى. إحداثيات نقطة انعطاف: في(1)=2.
رسم بياني للدالة في=(X+1)·( X–2) 2 يتقاطع مع محور الثور عند في=0، أي متى X= -1 و X=2;
يعبر محور أوي عند X=0، أي متى في=4. حصلنا على ثلاث نقاط: (-1؛ 0)، (2؛ 0)، (0؛ 4). سنقوم بإدخال جميع النقاط التي تم الحصول عليها في الجدول، وإضافة تلك المجاورة لها.
–2
–1



–16


يكون. 4 منحنى ص=(س+1)(س–2) 2.
المهمة رقم 1
نقدم لك المهام التي قد تحتوي على إجابة صحيحة واحدة أو اثنتين أو ثلاث أو أكثر. ضع دائرة حول أرقام جميع الإجابات الصحيحة.
1. إذا  ثم الوظيفة
ثم الوظيفة
1) زيادة
2) التناقص
3) ثابت
2. إذا
1) الزيادة
2) التناقص
3. إذا  ، ثم الدالة
، ثم الدالة
1) الزيادة
2) التناقص
4. إذا  ، ثم الدالة
، ثم الدالة
1) الزيادة. 3) النقصان
2) ثابت 4) رتيب
5. الوظيفة  يكون
يكون
1) حتى
2) ولا حتى
3) لا زوجي ولا فردي
4) الدورية
5) غير دورية
6) علم المثلثات
7) الابتدائية
6. الوظيفة  يكون
يكون
1) حتى
2) غريب
3) لا زوجي ولا فردي
4) الدورية
5) غير دورية
6) علم المثلثات
7) الابتدائية
2) فايرستراس 4) ديريشليت 6) لايبنتز
8) الحل  المعادلات
المعادلات
1) 0 3) 0 و 3 5) 2 7) 3
2) 2 و 3 4) 2 6) -5 و 1 8) 5 و 1
9) حل عدم المساواة 
1) ( ; 1) 3) (
; 1) 3) ( ; 1) 5) (-
; 1) 5) (- ;1)
;1)
2) (1; 5) 4) (2;  ) 6)
) 6) 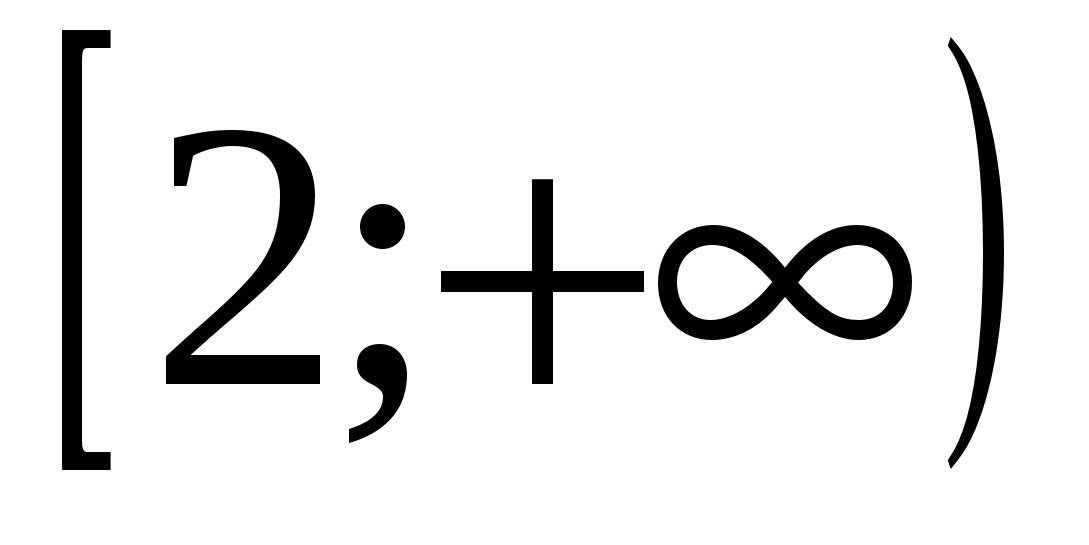
10) الطريقة  تم العثور على المبلغ
تم العثور على المبلغ
1) المتجهات
2) مستقيم
3) الجزء
11) إذا  ، ثم الدالة
، ثم الدالة
1) مقعرة 3) محدبة 5) متناقصة
2) رتابة 4) متزايدة 6) ثابت
12) مجال تعريف الدالة يساوي 
1) ( ;0)
;0)
2) (0;  )
)
3) (- ;
; )
)
4) (0;1)
5) 
6) 
7) (-1;1)
8) 
9) 
13) الوظيفة  يكون
يكون
1) إرشادية
2) علم المثلثات
3) القوة
4) لوغاريتمي
14) إذا كانت الوظائف ص = س  فهي كذلك
فهي كذلك 
1) حتى
2) غريب
3) لا زوجي ولا فردي
15) الوظيفة  في
في  يكون
يكون

 .
.



