Važan koncept u matematici je funkcija. Uz njegovu pomoć, možete vizualizirati mnoge procese koji se događaju u prirodi, odražavati odnos između određenih veličina pomoću formula, tablica i slika na grafikonu. Primjer je ovisnost tlaka sloja tekućine na tijelo o dubini uranjanja, ubrzanja - o djelovanju određene sile na predmet, porasta temperature - o prenesenoj energiji i mnogim drugim procesima. Proučavanje funkcije uključuje crtanje grafa, pronalaženje njenih svojstava, domena definicije i vrijednosti, intervala povećanja i smanjenja. Važna tačka u ovom procesu je pronalaženje ekstremnih tačaka. O tome kako to učiniti kako treba, a razgovor će se nastaviti.
O samom konceptu na konkretnom primjeru
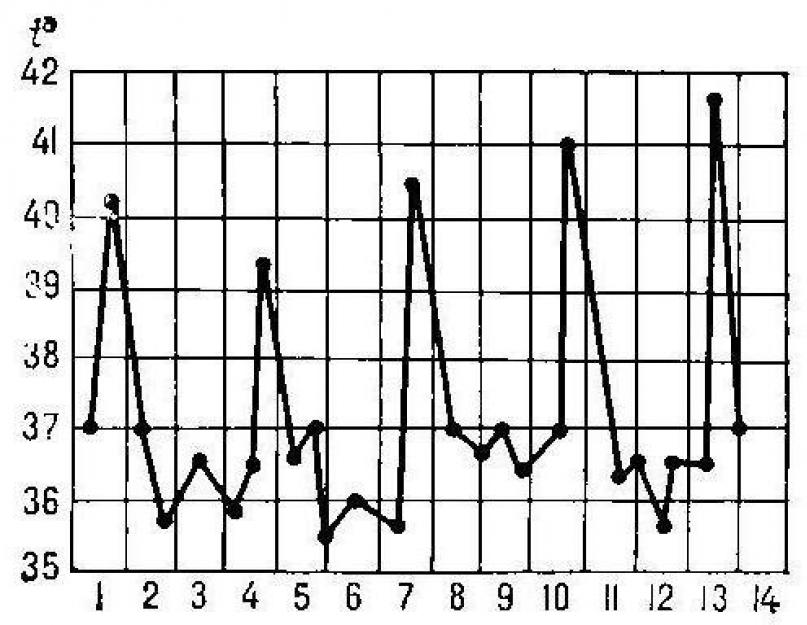
U medicini, izgradnja grafa funkcije može reći o toku razvoja bolesti u tijelu pacijenta, jasno odražavajući njegovo stanje. Pretpostavimo da je vrijeme u danima iscrtano duž ose OX, a temperatura ljudskog tijela duž ose OY. Slika jasno pokazuje kako ovaj indikator naglo raste, a zatim pada. Također je lako uočiti singularne točke koje odražavaju trenutke kada funkcija, nakon što se prethodno povećala, počinje opadati, i obrnuto. To su tačke ekstrema, odnosno kritične vrijednosti (maksimalne i minimalne) u ovaj slučaj temperaturu pacijenta, nakon čega dolazi do promjena u njegovom stanju.

Ugao nagiba
Sa slike je lako odrediti kako se derivacija funkcije mijenja. Ako se ravne linije grafikona povećavaju tokom vremena, onda je pozitivan. I što su strmiji, to su veća vrijednost poprima derivaciju kako se nagib raste. Tokom perioda smanjenja, ova vrijednost uzima negativne vrijednosti, okrećući se na nulu u tačkama ekstrema, a grafik derivacije u potonjem slučaju je povučen paralelno sa OX osom.
Svaki drugi proces treba tretirati na isti način. Ali najbolje u vezi ovog koncepta može reći pokret razna tijela, jasno prikazano na grafikonima.
Saobraćaj
Pretpostavimo da se neki objekt kreće pravolinijski, ravnomjerno dobijajući brzinu. U tom periodu promjena koordinata tijela grafički predstavlja određenu krivu, koju bi matematičar nazvao granom parabole. Istovremeno, funkcija se stalno povećava, jer se koordinatni indikatori mijenjaju sve brže i brže svake sekunde. Grafikon brzine pokazuje ponašanje derivacije, čija se vrijednost također povećava. To znači da pokret nema kritične tačke.
Ovo bi se nastavilo u nedogled. Ali šta ako tijelo iznenada odluči da uspori, stane i počne se kretati u drugom smjeru? U ovom slučaju, koordinatni indikatori će se početi smanjivati. A funkcija će proći kritičnu vrijednost i pretvoriti se iz rastuće u opadajuću.

U ovom primjeru opet možete razumjeti da se tačke ekstrema na grafu funkcije pojavljuju u trenucima kada ona prestane biti monotona.
Fizičko značenje izvedenice
Ono što je ranije opisano jasno je pokazalo da je derivacija u suštini stopa promjene funkcije. Ova prefinjenost sadrži svoje fizičko značenje. Ekstremne tačke su kritične oblasti na grafikonu. Moguće ih je saznati i otkriti izračunavanjem vrijednosti derivacije za koju se ispostavi da je jednaka nuli.
Postoji još jedan znak, koji je dovoljan uslov za ekstrem. Derivat na takvim mjestima fleksije mijenja svoj znak: od "+" do "-" u području maksimuma i od "-" do "+" u području minimuma.

Kretanje pod uticajem gravitacije
Zamislimo drugu situaciju. Djeca su je, igrajući se loptom, bacila na takav način da je počela da se kreće pod uglom prema horizontu. U početnom trenutku, brzina ovaj objekat bio najveći, ali je pod uticajem gravitacije počeo da se smanjuje, i to sa svakom sekundom za istu vrednost, jednaku približno 9,8 m/s 2. Ovo je vrijednost ubrzanja koje nastaje pod utjecajem zemljine gravitacije pri slobodnom padu. Na Mesecu bi bio oko šest puta manji.
Grafikon koji opisuje kretanje tijela je parabola s granama usmjerenim prema dolje. Kako pronaći ekstremne tačke? U ovom slučaju, ovo je vrh funkcije, gdje brzina tijela (kuglice) poprima nultu vrijednost. Izvod funkcije postaje nula. U tom slučaju se smjer, a time i vrijednost brzine, mijenja u suprotno. Tijelo sa svake sekunde leti sve brže i brže, a ubrzava za isto toliko - 9,8 m/s 2 .

Drugi derivat
U prethodnom slučaju, dijagram modula brzine je nacrtan kao prava linija. Ova linija je najpre usmerena naniže, jer se vrednost ove veličine stalno smanjuje. Nakon dostizanja nule u jednoj od vremenskih tačaka, indikatori ove vrijednosti počinju rasti, a smjer grafičkog prikaza modula brzine dramatično se mijenja. Sada je linija usmjerena prema gore.
Brzina, kao derivacija koordinate u odnosu na vrijeme, također ima kritičnu tačku. U ovoj regiji, funkcija, koja se u početku smanjuje, počinje rasti. Ovo je mjesto tačke ekstrema derivacije funkcije. U ovom slučaju, nagib tangente postaje nula. A ubrzanje, kao drugi izvod koordinate u odnosu na vrijeme, mijenja predznak iz “-” u “+”. A kretanje od ravnomjerno sporog postaje ravnomjerno ubrzano.
Grafikon ubrzanja
Sada razmotrite četiri brojke. Svaki od njih prikazuje grafikon promjene tokom vremena fizička količina poput ubrzanja. U slučaju "A", njegova vrijednost ostaje pozitivna i konstantna. To znači da se brzina tijela, kao i njegova koordinata, stalno povećava. Ako zamislimo da će se objekt kretati na ovaj način beskonačno dugo, ispostavit će se da se funkcija koja odražava ovisnost koordinate o vremenu stalno povećava. Iz ovoga proizilazi da nema kritičnih područja. Na grafu derivacije također nema ekstremnih tačaka, odnosno linearno promjenjive brzine.

Isto važi i za slučaj "B" sa pozitivnim i stalno rastućim ubrzanjem. Istina, ovdje će grafikoni za koordinate i brzinu biti nešto složeniji.
Kada ubrzanje padne na nulu
Gledajući figuru "B", može se uočiti potpuno drugačija slika koja karakterizira kretanje tijela. Njegova brzina će biti grafički prikazana kao parabola s granama okrenutim prema dolje. Ako nastavimo liniju koja opisuje promjenu ubrzanja sve dok se ne siječe s osom OX, i dalje, onda možemo zamisliti da će se do ove kritične vrijednosti, gdje se ispostavi da je ubrzanje jednako nuli, brzina objekta povećati sve sporije. Ekstremna tačka derivacije koordinatne funkcije bit će tik na vrhu parabole, nakon čega će tijelo radikalno promijeniti prirodu kretanja i početi se kretati u drugom smjeru.
U potonjem slučaju, "G", priroda kretanja se ne može precizno odrediti. Ovdje samo znamo da nema ubrzanja za neki period koji se razmatra. To znači da predmet može ostati na mjestu ili se kretanje odvija konstantnom brzinom.
Problem sa sabiranjem koordinata
Pređimo na zadatke koji se često susreću prilikom učenja algebre u školi i koji se nude za pripremu ispita. Slika ispod prikazuje graf funkcije. Potrebno je izračunati zbir bodova ekstrema.

To ćemo učiniti za y-osu određivanjem koordinata kritičnih područja u kojima se uočava promjena karakteristika funkcije. Jednostavno rečeno, nalazimo vrijednosti duž x-ose za točke pregiba, a zatim nastavljamo sa dodavanjem rezultirajućih pojmova. Prema grafikonu, vidljivo je da imaju sljedeće vrijednosti: -8; -7; -5; -3; -2; jedan; 3. Ovo daje -21, što je odgovor.
Optimalno rješenje
Nije potrebno objašnjavati koliko izbor optimalnog rješenja može biti važan u izvođenju praktičnih zadataka. Na kraju krajeva, postoji mnogo načina da se postigne cilj, a najbolji izlaz, u pravilu, je samo jedan. To je izuzetno potrebno, na primjer, prilikom projektovanja brodova, svemirski brodovi i aviona, arhitektonskih objekata kako bi se pronašao optimalni oblik ovih objekata koje je napravio čovjek.

Brzina vozila uvelike ovisi o kompetentnom minimiziranju otpora koji doživljavaju pri kretanju kroz vodu i zrak, o preopterećenjima koja nastaju pod utjecajem gravitacijskih sila i mnogim drugim pokazateljima. Brodu na moru su potrebne takve kvalitete kao što je stabilnost tokom oluje; za riječni brod je važan minimalni gaz. Prilikom izračunavanja optimalnog dizajna, tačke ekstrema na grafu mogu vizualno dati ideju o najboljem rješenju složenog problema. Zadaci takvog plana često se rješavaju u privredi, u privrednim oblastima, u mnogim drugim životnim situacijama.
Iz antičke istorije
Ekstremni zadaci zaokupljali su čak i drevne mudrace. Grčki naučnici uspješno su razotkrili misteriju površina i volumena kroz matematičke proračune. Oni su prvi shvatili da na ravni različitih figura istog perimetra, najveća površina uvek ima krug. Slično tome, lopta ima maksimalan volumen među ostalim objektima u prostoru sa istom površinom. Posvećeni rješavanju ovakvih problema poznate ličnosti poput Arhimeda, Euklida, Aristotela, Apolonija. Heron je vrlo dobro uspio pronaći ekstremne tačke, koji je, pribjegavši proračunima, izgradio genijalne uređaje. To su uključivale automatske mašine koje se kreću pomoću pare, pumpe i turbine koje rade na istom principu.

Izgradnja Kartage
Postoji legenda čija se radnja zasniva na rješavanju jednog od ekstremnih zadataka. Rezultat poslovnog pristupa koji je pokazala feničanska princeza, koja se obratila mudracima za pomoć, bila je izgradnja Kartage. Zemljište za ovaj drevni i slavni grad, Didonu (tako se zvao vladar) predstavio je vođa jednog od afričkih plemena. Površina parcele mu se isprva nije činila jako velikom, jer je prema ugovoru morala biti prekrivena volovskom kožom. Ali princeza je naredila svojim vojnicima da ga iseku na tanke trake i od njih naprave pojas. Ispostavilo se da je bio toliko dugačak da je pokrivao područje na kojem je stao cijeli grad.
Poreklo računa
A sada pređimo iz antičkih vremena u kasniju eru. Zanimljivo je da je u 17. veku Keplera potaknuo da razume osnove matematičke analize susretom sa prodavcem vina. Trgovac je bio toliko upućen u svoju profesiju da je lako mogao odrediti količinu pića u buretu jednostavnim spuštanjem željeznog podveza u nju. Razmišljajući o takvoj radoznalosti, čuveni naučnik je uspeo da sam reši ovu dilemu. Ispostavilo se da su se tadašnji vješti bačvari odvikli od izrade posuda na način da na određenoj visini i poluprečniku obima prstenova za pričvršćivanje imaju maksimalan kapacitet.
Ovo je za Keplera postalo povod za dalje razmišljanje. Do optimalnog rješenja Bochari su došli dugim traženjem, greškama i novim pokušajima, prenoseći svoje iskustvo s generacije na generaciju. Ali Kepler je želio ubrzati proces i naučiti kako to učiniti za kratko vrijeme kroz matematičke proračune. Sav njegov razvoj, koji su pokupili kolege, pretvorio se u sada poznate teoreme Fermata i Newtona - Leibniza.
Problem pronalaženja maksimalne površine
Zamislite da imamo žicu čija je dužina 50 cm.Kako od nje napraviti pravougaonik koji ima najveću površinu?
Polazeći od odluke treba poći od jednostavnih i dobro poznatih istina. Jasno je da će obim naše figure biti 50 cm. Također se sastoji od dvostrukih dužina obje strane. To znači da, nakon što je jedan od njih označen kao "X", drugi se može izraziti kao (25 - X).
Odavde dobijamo površinu jednaku X (25 - X). Ovaj izraz se može predstaviti kao funkcija koja poprima mnogo vrijednosti. Rješenje problema zahtijeva pronalaženje maksimuma od njih, što znači da treba pronaći tačke ekstrema.
Da bismo to učinili, nalazimo prvi izvod i izjednačavamo ga sa nulom. Rezultat je jednostavna jednadžba: 25 - 2X = 0.
Iz njega saznajemo da je jedna od stranica X = 12,5.
Dakle, još jedno: 25 - 12,5 = 12,5.
Ispada da će rješenje problema biti kvadrat sa stranicom od 12,5 cm.

Kako pronaći maksimalnu brzinu
Razmotrimo još jedan primjer. Zamislite da postoji tijelo čije je pravolinijsko kretanje opisano jednačinom S = - t 3 + 9t 2 - 24t - 8, gdje je pređeni put izražen u metrima, a vrijeme u sekundama. Potrebno je pronaći maksimalnu brzinu. Kako uraditi? Preuzeto pronađite brzinu, odnosno prvu derivaciju.
Dobijamo jednačinu: V = - 3t 2 + 18t - 24. Sada, da bismo riješili problem, opet moramo pronaći tačke ekstrema. Ovo se mora uraditi na isti način kao u prethodnom zadatku. Pronalazimo prvi izvod brzine i izjednačavamo ga sa nulom.
Dobijamo: - 6t + 18 = 0. Otuda je t = 3 s. Ovo je vrijeme kada brzina tijela poprima kritičnu vrijednost. Dobijene podatke zamjenjujemo u jednačinu brzine i dobijamo: V = 3 m/s.
Ali kako znaš šta je to maksimalna brzina, jer kritične tačke funkcije mogu biti njene najveće ili najmanje vrijednosti? Da biste provjerili, morate pronaći drugi izvod brzine. Izražava se kao broj 6 sa znakom minus. To znači da je pronađena tačka maksimum. A u slučaju pozitivne vrijednosti druge derivacije, postojao bi minimum. Dakle, pronađeno rješenje je bilo ispravno.
Zadaci dati kao primjer samo su dio onih koji se mogu riješiti pronalaženjem ekstremnih tačaka funkcije. U stvari, ima ih mnogo više. A takvo znanje otvara neograničene mogućnosti ljudskoj civilizaciji.
Kao što vidite, ovaj znak ekstrema funkcije zahtijeva postojanje derivacije barem do drugog reda u tački .
Primjer.
Pronađite ekstreme funkcije .
Rješenje.
Počnimo od obima: 
Hajde da razlikujemo originalnu funkciju: 
x=1, odnosno to je tačka mogućeg ekstremuma. Pronalazimo drugi izvod funkcije i izračunavamo njegovu vrijednost na x=1:

Prema tome, drugim dovoljnim ekstremnim uslovom, x=1- maksimalni poen. Onda  je maksimum funkcije.
je maksimum funkcije.
Grafička ilustracija.

odgovor:
![]()
Treći dovoljan uslov za ekstremum funkcije.
Neka funkcija y=f(x) ima derivate do n-ti red u -okolici tačke i derivacije do n+1 red u samoj tački. Neka i .
Primjer.
Pronađite ekstremne tačke funkcije ![]() .
.
Rješenje.
Originalna funkcija je čitava racionalna, njena domena definicije je čitav skup realnih brojeva.
Hajde da razlikujemo funkciju: 
Izvod nestaje kada ![]() , dakle, ovo su tačke mogućeg ekstremuma. Koristimo treći dovoljan uslov za ekstrem.
, dakle, ovo su tačke mogućeg ekstremuma. Koristimo treći dovoljan uslov za ekstrem.
Pronalazimo drugu derivaciju i izračunavamo njenu vrijednost u tačkama mogućeg ekstremuma (izostavićemo posredne proračune): 
Dakle, je maksimalna tačka (za treći dovoljan znak ekstremuma imamo n=1 i ).
Da razjasnimo prirodu tačaka ![]() pronađite treći izvod i izračunajte njegovu vrijednost u ovim tačkama:
pronađite treći izvod i izračunajte njegovu vrijednost u ovim tačkama: 
Prema tome, je tačka infleksije funkcije ( n=2 i ).
Ostaje da se pozabavimo poentom. Pronalazimo četvrti izvod i izračunavamo njegovu vrijednost u ovoj tački: 
Dakle, to je minimalna tačka funkcije.
Grafička ilustracija.

odgovor:
Maksimalna tačka je minimalna tačka funkcije.
10. Ekstremumi funkcije Definicija ekstrema
Poziva se funkcija y = f(x). povećanje (opadanje) u nekom intervalu ako je za x 1< x 2 выполняется неравенство (f(x 1) < f (x 2) (f(x 1) >f(x2)).
Ako se diferencijabilna funkcija y = f(x) na segmentu povećava (smanjuje), tada njen izvod na ovom segmentu f "(x) 0
(f "(x) 0).
Dot x o pozvao lokalna maksimalna tačka (minimum) funkcije f(x) ako postoji susjedstvo tačke x o, za sve tačke za koje je tačna nejednakost f(x) ≤ f(x o) (f(x) ≥ f(x o)).
Pozivaju se maksimalne i minimalne tačke ekstremne tačke, a vrijednosti funkcije u tim točkama su njene extrema.
ekstremne tačke
Neophodni uslovi za ekstrem. Ako tačka x o je tačka ekstrema funkcije f (x), tada ili f "(x o) = 0, ili f (x o) ne postoji. Takve tačke se nazivaju kritičan, gdje je sama funkcija definirana u kritičnoj tački. Ekstreme funkcije treba tražiti među njenim kritičnim tačkama.
Prvi dovoljan uslov. Neka x o- kritična tačka. Ako je f "(x) prilikom prolaska kroz tačku x o mijenja znak plus u minus, a zatim u tački x o funkcija ima maksimum, inače ima minimum. Ako derivacija ne promijeni predznak pri prolasku kroz kritičnu tačku, onda u tački x o ne postoji ekstremum.
Drugi dovoljan uslov. Neka funkcija f(x) ima izvod f"(x) u okolini tačke x o i drugi derivat u samoj tački x o. Ako je f "(x o) \u003d 0,\u003e 0 (<0), то точка x o je lokalna tačka minimuma (maksimuma) funkcije f(x). Ako je =0, onda se mora koristiti ili prvi dovoljan uslov ili uključiti više izvode.
Na segmentu, funkcija y = f(x) može dostići svoju minimalnu ili maksimalnu vrijednost bilo u kritičnim tačkama ili na krajevima segmenta.
Primjer 3.22. Naći ekstreme funkcije f(x) = 2x 3 - 15x 2 + 36x - 14.
Rješenje. Budući da je f "(x) = 6x 2 - 30x +36 = 6 (x - 2) (x - 3), onda su kritične tačke funkcije x 1 = 2 i x 2 = 3. Ekstremne tačke mogu biti samo u ovim tačkama. Dakle, kada prolazi kroz tačku x 1 \u003d 2, derivacija mijenja znak plus u minus, tada u ovoj tački funkcija ima maksimum. Prilikom prolaska kroz tačku x 2 = 3, derivacija mijenja predznak minus u plus, dakle, u tački x 2 \u003d 3, funkcija ima minimum. Izračunavši vrijednosti funkcije u tačkama x 1 = 2 i x 2 = 3, nalazimo ekstreme od funkcija: maksimalno f (2) = 14 i minimalno f (3) = 13.
Razmotrimo graf neprekidne funkcije y=f(x) prikazano na slici.
Vrijednost funkcije u tački x 1 će biti veći od vrijednosti funkcije u svim susjednim točkama i lijevo i desno od x jedan . U ovom slučaju se kaže da funkcija ima u tački x 1 max. U tački x Funkcija 3 očito također ima maksimum. Ako uzmemo u obzir poentu x 2, tada je vrijednost funkcije u njemu manja od svih susjednih vrijednosti. U ovom slučaju se kaže da funkcija ima u tački x 2 minimum. Slično za poentu x 4 .
Funkcija y=f(x) u tački x 0 ima maksimum, ako je vrijednost funkcije u ovoj tački veća od njenih vrijednosti u svim točkama nekog intervala koji sadrži točku x 0 , tj. ako postoji takva okolina tačke x 0, što je za sve x≠x 0 , koji pripada ovoj četvrti, imamo nejednakost f(x)<f(x 0 ) .
Funkcija y=f(x) Ima minimum u tački x 0 , ako postoji takva okolina tačke x 0 , šta je za svakoga x≠x 0 koji pripada ovoj četvrti, imamo nejednakost f(x)>f(x0.
Tačke u kojima funkcija dostiže svoj maksimum i minimum nazivaju se točke ekstrema, a vrijednosti funkcije u tim točkama su ekstremi funkcije.
Obratimo pažnju na činjenicu da funkcija definisana na segmentu može dostići svoj maksimum i minimum samo u tačkama koje se nalaze unutar segmenta koji se razmatra.
Imajte na umu da ako funkcija ima maksimum u nekoj tački, to ne znači da u ovom trenutku funkcija ima maksimalnu vrijednost u cijeloj domeni. Na gornjoj slici, funkcija u tački x 1 ima maksimum, iako postoje tačke u kojima su vrijednosti funkcije veće nego u tački x 1 . posebno, f(x 1) < f(x 4) tj. minimum funkcije je veći od maksimuma. Iz definicije maksimuma samo slijedi da je to najveća vrijednost funkcije u tačkama koje su dovoljno blizu tačke maksimuma.
Teorema 1. (Neophodan uslov za postojanje ekstrema.) Ako je diferencijabilna funkcija y=f(x) ima u tački x=x 0 ekstremu, onda njegov derivat u ovoj tački nestaje.
Dokaz. Neka, radi određenosti, u tački x 0 funkcija ima maksimum. Zatim za dovoljno male inkremente Δ x imamo f(x 0 + Δ x)
Prenoseći ove nejednakosti do granice kao Δ x→ 0 i uzimajući u obzir da je izvod f "(x 0) postoji, pa stoga granica na lijevoj strani ne ovisi o tome kako Δ x→ 0, dobijamo: za Δ x → 0 – 0 f"(x 0) ≥ 0 i na Δ x → 0 + 0 f"(x 0) ≤ 0. Pošto f"(x 0) definira broj, onda su ove dvije nejednakosti kompatibilne samo ako f"(x 0) = 0.
Dokazana teorema kaže da maksimum i minimum točke mogu biti samo među onim vrijednostima argumenta za koje derivacija nestaje.
Razmotrili smo slučaj kada funkcija ima derivaciju u svim tačkama određenog segmenta. Šta se dešava kada izvod ne postoji? Razmotrite primjere.
Primjeri.
- y=|x|.
Funkcija nema izvod u tački x=0 (u ovom trenutku graf funkcije nema definitivnu tangentu), ali u ovom trenutku funkcija ima minimum, jer y(0)=0, i za sve x≠ 0y > 0.
- Neka x< x
0 . Onda c< x
0 i f "(c)> 0.
Zbog toga f "(c)(x-x 0)<
0 i, prema tome,
f(x) - f(x 0 )< 0, tj. f(x)< f(x 0 ).
- Neka x > x 0 . Onda c> x 0 i f"(c)< 0. Sredstva f "(c)(x-x 0)< 0. Zbog toga f(x) - f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
- Pronađite opseg funkcije f(x).
- Pronađite prvi izvod funkcije f"(x).
- Odredite kritične tačke, za ovo:
- pronađite prave korijene jednačine f"(x)=0;
- pronađite sve vrijednosti x pod kojim derivat f"(x) ne postoji.
- Odredite predznak derivacije lijevo i desno od kritične tačke. Pošto predznak izvoda ostaje konstantan između dvije kritične tačke, dovoljno je odrediti predznak izvoda u bilo kojoj tački lijevo i u jednoj tački desno od kritične tačke.
- Izračunajte vrijednost funkcije u tačkama ekstrema.
- Pronađite sve kritične tačke funkcije u intervalu ( a, b) i izračunajte vrijednosti funkcije u tim točkama.
- Izračunajte vrijednosti funkcije na krajevima segmenta za x=a, x=b.
- Od svih dobijenih vrijednosti odaberite najveću i najmanju.

Funkcija nema izvod at x=0, pošto ide u beskonačnost kada x=0. Ali u ovom trenutku funkcija ima maksimum.
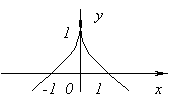
Funkcija nema izvod at x=0 jer ![]() at x→0. U ovom trenutku funkcija nema ni maksimum ni minimum. stvarno, f(x)=0 i at x<0f(x)<0, а при x>0f(x)>0.
at x→0. U ovom trenutku funkcija nema ni maksimum ni minimum. stvarno, f(x)=0 i at x<0f(x)<0, а при x>0f(x)>0.

Dakle, iz datih primera i formulisane teoreme jasno je da funkcija može imati ekstrem samo u dva slučaja: 1) u tačkama gde izvod postoji i jednak je nuli; 2) u tački u kojoj izvod ne postoji.
Međutim, ako u nekom trenutku x 0 mi to znamo f"(x 0 ) =0, onda se iz ovoga ne može zaključiti da je u tački x 0 funkcija ima ekstrem.
Na primjer. ![]() .
.

Ali poenta x=0 nije tačka ekstrema, jer se lijevo od ove tačke vrijednosti funkcije nalaze ispod ose Ox, i iznad desno.
Vrijednosti argumenta iz domene funkcije, za koje derivacija funkcije nestaje ili ne postoji, nazivaju se kritične tačke.
Iz prethodnog proizilazi da su tačke ekstrema funkcije među kritičnim tačkama, ali, međutim, nije svaka kritična tačka tačka ekstrema. Stoga, da biste pronašli ekstremu funkcije, morate pronaći sve kritične točke funkcije, a zatim ispitati svaku od ovih tačaka zasebno za maksimum i minimum. Za to služi sljedeća teorema.
Teorema 2. (dovoljan uslov za postojanje ekstremuma.) Neka je funkcija kontinuirana na nekom intervalu koji sadrži kritičnu tačku x 0 , i diferencibilan je u svim tačkama ovog intervala (osim, možda, same tačke x 0). Ako pri prolasku s lijeva na desno kroz ovu tačku derivacija promijeni predznak sa plusa na minus, tada u tački x = x 0 funkcija ima maksimum. Ako, prilikom prolaska x 0 s lijeva na desno, derivacija mijenja predznak iz minusa u plus, tada funkcija ima minimum u ovoj tački.
Dakle, ako
Dokaz. Pretpostavimo prvo da kada prolazimo x 0, derivacija mijenja predznak iz plusa u minus, tj. za sve x blizu tačke x 0 f "(x)> 0 for x< x 0 , f"(x)< 0 for x > x 0 . Primijenimo Lagrangeov teorem na razliku f(x) - f(x 0 ) = f "(c)(x- x 0), gdje c leži između x i x 0 .
Dakle, za sve vrijednosti x dovoljno blizu x 0 f(x)< f(x 0 ) . A to znači da u ovom trenutku x 0 funkcija ima maksimum.
Slično se dokazuje i drugi dio minimalne teoreme.
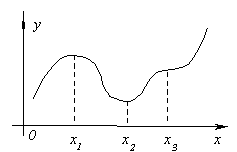
Ilustrujmo značenje ove teoreme na slici. Neka f"(x 1 ) =0 i za bilo koje x, dovoljno blizu x 1, nejednakosti
f"(x)< 0 at x< x 1 , f "(x)> 0 at x > x 1 .
Zatim lijevo od tačke x 1 funkcija raste, a desno opada, dakle, kada x = x 1 funkcija ide od povećanja ka opadajućoj, odnosno ima maksimum.
Slično, mogu se razmotriti tačke x 2 i x 3 .

Šematski se sve navedeno može prikazati na slici:
Pravilo za proučavanje funkcije y=f(x) za ekstrem
Primjeri. Istražite funkcije za minimum i maksimum.
NAJVEĆE I MINIMALNE VRIJEDNOSTI FUNKCIJE NA PRESETKU
najveći vrijednost funkcije na segmentu je najveća od svih njenih vrijednosti na ovom segmentu, i najmanje je najmanja od svih njegovih vrijednosti.
Razmotrite funkciju y=f(x) kontinuirano na intervalu [ a, b]. Kao što je poznato, takva funkcija dostiže svoje maksimalne i minimalne vrijednosti, bilo na granici segmenta, bilo unutar njega. Ako je maksimalna ili minimalna vrijednost funkcije dostignuta u unutrašnjoj tački segmenta, tada je ta vrijednost maksimalna ili minimalna vrijednost funkcije, odnosno dostiže se u kritičnim tačkama.
Tako dobijamo sledeće pravilo za pronalaženje najveće i najmanje vrijednosti funkcije na segmentu [ a, b] :
Povećanje, smanjenje i ekstremi funkcije
Pronalaženje intervala povećanja, smanjenja i ekstrema funkcije je i samostalan zadatak i važan dio drugih zadataka, posebno, studija pune funkcije. Date su početne informacije o porastu, smanjenju i ekstremima funkcije teorijsko poglavlje o izvodu, što toplo preporučujem za preliminarnu studiju (ili ponavljanje)- također iz razloga što je sljedeći materijal zasnovan na samom suština derivatašto je skladan nastavak ovog članka. Mada, ako vrijeme ističe, onda je moguća i čisto formalna razrada primjera današnje lekcije.
I danas je u zraku duh rijetke jednodušnosti i direktno osjećam da svi prisutni gore od želje naučiti istraživati funkciju koristeći derivat. Stoga se razumna dobra vječna terminologija odmah pojavljuje na ekranima vaših monitora.
Zašto? Jedan od najpraktičnijih razloga je: da vam bude jasno šta se generalno traži od vas u određenom zadatku!
Monotonost funkcije. Ekstremne tačke i ekstremi funkcije
Razmotrimo neku funkciju. Pojednostavljeno, pretpostavljamo da kontinuirano na cijeloj brojevnoj pravoj:

Za svaki slučaj, odmah ćemo se riješiti mogućih iluzija, posebno za one čitatelje koji su se nedavno upoznali sa intervali konstantnosti predznaka funkcije. Sada mi NEZAINTERESOVAN, kako se graf funkcije nalazi u odnosu na osu (iznad, ispod, gdje prelazi os). Za uvjerljivost, mentalno obrišite osi i ostavite jedan grafikon. Jer interes je u tome.
Funkcija povećava na intervalu ako je za bilo koje dvije točke ovog intervala povezane relacijom , nejednakost je istinita. To jest, veća vrijednost argumenta odgovara većoj vrijednosti funkcije, a njen graf ide „odozdo prema vrhu“. Demo funkcija raste u intervalu .
Isto tako, funkcija opadajući na intervalu ako za bilo koje dvije točke danog intervala, tako da je , nejednakost je istinita. Odnosno, veća vrijednost argumenta odgovara manjoj vrijednosti funkcije, a njen graf ide „od vrha do dna“. Naša funkcija se smanjuje tokom intervala ![]() .
.
Ako se funkcija povećava ili smanjuje u intervalu, onda se ona poziva strogo monotono na ovom intervalu. Šta je monotonost? Shvatite to doslovno - monotonija.
Također je moguće definirati neopadajući funkcija (opušteno stanje u prvoj definiciji) i bez povećanja funkcija (ublaženi uslov u 2. definiciji). Funkcija koja se ne opada ili ne raste na intervalu naziva se monotonom funkcijom na datom intervalu (stroga monotonost je poseban slučaj "samo" monotonosti).
Teorija također razmatra i druge pristupe određivanju povećanja / smanjenja funkcije, uključujući polu-intervali, segmente, ali kako vam ne bismo sipali ulje-ulje-ulje na glavu, pristajemo da radimo s otvorenim intervalima sa kategoričkim definicijama - ovo je jasnije i sasvim dovoljno za rješavanje mnogih praktičnih problema.
Na ovaj način, u mojim člancima, formulacija “monotonost funkcije” će se gotovo uvijek sakriti intervalima stroga monotonija(strogo povećanje ili strogo smanjenje funkcije).
Point susjedstvo. Riječi nakon kojih se učenici razbacuju gdje god mogu, i užasnuto se skrivaju po uglovima. …Iako nakon objave Cauchy granice vjerovatno se više ne kriju, već se samo lagano zadrhte =) Ne brinite, sada neće biti dokaza o teoremama matematičke analize - trebao mi je susjedstvo da rigoroznije formuliram definicije ekstremne tačke. pamtimo:
Neighbourhood point imenuje interval koji sadrži datu tačku, dok se radi pogodnosti često pretpostavlja da je interval simetričan. Na primjer, tačka i njeno standardno susjedstvo:
U osnovi definicije:
Tačka se zove stroga maksimalna tačka, ako postoji njen komšiluk, za sve vrijednosti od kojih je, osim same tačke, nejednakost ispunjena. U našem konkretnom primjeru, ovo je poenta.
Tačka se zove stroga minimalna tačka, ako postoji njen komšiluk, za sve vrijednosti od kojih je, osim same tačke, nejednakost ispunjena. Na crtežu - tačka "a".
Bilješka : zahtjev da susjedstvo bude simetrično uopće nije potrebno. Osim toga, važno je sama činjenica postojanja susjedstvo (iako sićušno, čak i mikroskopsko) koje zadovoljava navedene uslove
Tačke se zovu tačke strogog ekstrema ili jednostavno ekstremne tačke funkcije. Odnosno, to je generalizovani termin za maksimalne i minimalne poene.
Kako razumjeti riječ "ekstremum"? Da, direktno kao i monotonija. Ekstremne tačke rolerkostera.
Kao iu slučaju monotonosti, u teoriji postoje i još češći nestrogi postulati (pod koje, naravno, spadaju smatrani strogi slučajevi!):
Tačka se zove maksimalni poen, ako postoji njegovu okolinu, tako da za sve
Tačka se zove minimalna tačka, ako postoji njegovu okolinu, tako da za sve vrijednosti ovog susjedstva, vrijedi nejednakost.
Imajte na umu da se prema posljednje dvije definicije, svaka tačka konstantne funkcije (ili „ravno područje“ neke funkcije) smatra i maksimalnom i minimalnom točkom! Funkcija je, inače, i nerastuća i neopadajuća, odnosno monotona. Međutim, te argumente prepuštamo teoretičarima, jer u praksi gotovo uvijek razmišljamo o tradicionalnim "brdima" i "udubinama" (vidi crtež) sa jedinstvenim "kraljem brda" ili "močvarnom princezom". Kao varijanta, javlja se tačka, usmjeren gore ili dolje, na primjer, minimum funkcije u točki .
Oh, i kad smo kod kraljevske porodice:
- značenje se zove maksimum funkcije;
- značenje se zove minimum funkcije.
Uobičajeno ime - ekstremi funkcije.
Molimo budite oprezni sa svojim riječima!
ekstremne tačke su "x" vrijednosti.
Ekstremi- vrijednosti "igre".
! Bilješka : ponekad se navedeni pojmovi odnose na tačke "x-y" koje leže direktno na GRAFIKU funkcije.
Koliko ekstrema može imati funkcija?
Ništa, 1, 2, 3, … itd. do beskonačnosti. Na primjer, sinus ima beskonačan broj minimuma i maksimuma.
BITAN! Izraz "maksimalna funkcija" nije identično izraz "maksimalna vrijednost funkcije". Lako je uočiti da je vrijednost maksimalna samo u ovdašnjoj četvrti, a u gornjem lijevom kutu su „naglo drugovi“. Isto tako, "minimalna funkcija" nije isto što i "minimalna vrijednost funkcije", a na crtežu možemo vidjeti da je vrijednost minimalna samo na određenom području. U tom smislu se nazivaju i ekstremne tačke lokalne ekstremne tačke, i ekstremi lokalni ekstremi. Oni šetaju i lutaju okolo i globalno braćo. Dakle, svaka parabola ima na svom vrhu globalni minimum ili globalni maksimum. Nadalje, neću praviti razliku između vrsta ekstrema, a objašnjenje je izraženo više u općeobrazovne svrhe - dodatni pridjevi "lokalni" / "globalni" ne bi trebali biti iznenađeni.
Sumirajmo našu kratku digresiju u teoriju uz kontrolni snimak: šta podrazumijeva zadatak „pronaći intervale monotonosti i ekstremne tačke funkcije“?
Formulacija traži da se pronađe:
- intervali povećanja / smanjenja funkcije (neopadajući, nerastući se pojavljuju mnogo rjeđe);
– maksimalne i/ili minimalne bodove (ako ih ima). Pa, bolje je pronaći minimume/maksimume iz neuspjeha ;-)
Kako sve ovo definisati? Uz pomoć derivacijske funkcije!
Kako pronaći intervale povećanja, smanjenja,
ekstremne tačke i ekstremumi funkcije?
Mnoga pravila su, zapravo, već poznata i shvaćena lekcija o značenju izvedenice.
Tangentni derivat ![]() nosi dobre vijesti da se funkcija sve više povećava domene.
nosi dobre vijesti da se funkcija sve više povećava domene.
Sa kotangensom i njegovim derivatom ![]() situacija je upravo suprotna.
situacija je upravo suprotna.
Arksinus raste na intervalu - izvod je ovdje pozitivan: ![]() .
.
Za , funkcija je definirana, ali nije diferencibilna. Međutim, u kritičnoj tački postoje desna derivacija i desna tangenta, a na drugoj ivici njihovi lijevi parnjaci.
Mislim da vam neće biti teško izvesti slično rezoniranje za arc kosinus i njegovu derivaciju.
Svi ovi slučajevi, od kojih mnogi jesu tabelarne izvedenice, podsjećam, pratite direktno iz definicije derivata.
Zašto istraživati funkciju s derivatom?
Da biste dobili bolju predstavu o tome kako izgleda graf ove funkcije: gdje ide "odozdo prema gore", gdje ide "od vrha prema dolje", gdje dostiže najniže razine (ako uopće). Nisu sve funkcije tako jednostavne - u većini slučajeva generalno nemamo ni najmanju ideju o grafu određene funkcije.
Vrijeme je da pređemo na značajnije primjere i razmotrimo algoritam za pronalaženje intervala monotonosti i ekstrema funkcije:
Primjer 1
Pronađite intervale povećanja/spadanja i ekstreme funkcije
![]()
Rješenje:
1) Prvi korak je pronaći opseg funkcije, a također zabilježite tačke prekida (ako postoje). U ovom slučaju, funkcija je kontinuirana na cijeloj realnoj liniji, a ova radnja je donekle formalna. Ali u nekim slučajevima ovdje se razbuktaju ozbiljne strasti, pa hajde da se prema paragrafu odnosimo bez zanemarivanja.
2) Druga tačka algoritma je dospjela
neophodan uslov za ekstrem:
Ako u tački postoji ekstremum, tada vrijednost ili ne postoji.
Zbunjeni zbog kraja? Ekstremum funkcije "modulo x" .
uslov je neophodan, ali nije dovoljno, a obrnuto nije uvijek tačno. Dakle, iz jednakosti još ne slijedi da funkcija doseže maksimum ili minimum u točki . Klasičan primjer je već osvijetljen iznad - ovo je kubna parabola i njena kritična tačka.
Ali kako god bilo, neophodni uslov za ekstrem diktira potrebu za pronalaženjem sumnjivih tačaka. Da biste to učinili, pronađite izvod i riješite jednačinu:
Na početku prvog članka o grafovima funkcija Rekao sam vam kako brzo izgraditi parabolu koristeći primjer ![]() : "... uzimamo prvi izvod i izjednačavamo ga sa nulom: ... Dakle, rješenje naše jednadžbe: - u ovoj tački se nalazi vrh parabole ...". Sada, mislim da je svima jasno zašto je vrh parabole upravo u ovoj tački =) Uopšteno govoreći, ovdje bi trebali početi sa sličnim primjerom, ali je previše jednostavan (čak i za čajnik). Osim toga, postoji analog na samom kraju lekcije o derivirajuća funkcija. Pa da podignemo nivo:
: "... uzimamo prvi izvod i izjednačavamo ga sa nulom: ... Dakle, rješenje naše jednadžbe: - u ovoj tački se nalazi vrh parabole ...". Sada, mislim da je svima jasno zašto je vrh parabole upravo u ovoj tački =) Uopšteno govoreći, ovdje bi trebali početi sa sličnim primjerom, ali je previše jednostavan (čak i za čajnik). Osim toga, postoji analog na samom kraju lekcije o derivirajuća funkcija. Pa da podignemo nivo:
Primjer 2
Pronađite intervale monotonosti i ekstreme funkcije
Ovo je "uradi sam" primjer. Kompletno rješenje i približan završni uzorak problema na kraju lekcije.
Došao je dugo očekivani trenutak susreta sa frakcionim racionalnim funkcijama:
Primjer 3
Istražite funkciju koristeći prvi izvod
Obratite pažnju na to kako se varijantno može preformulisati jedan te isti zadatak.
Rješenje:
1) Funkcija trpi beskonačne prekide u točkama .
2) Otkrivamo kritične tačke. Nađimo prvi izvod i izjednačimo ga sa nulom: 
Hajde da riješimo jednačinu. Razlomak je nula kada mu je brojilac nula:
Tako dobijamo tri kritične tačke: ![]()
3) Odvojite SVE otkrivene tačke na brojevnoj pravoj i intervalna metoda definisati predznake DERIVATA:
Podsjećam vas da trebate uzeti neku tačku intervala, izračunati vrijednost derivacije u njoj ![]() i odredi njegov predznak. Isplativije je ni ne brojati, već verbalno „procenjivati“. Uzmite, na primjer, tačku koja pripada intervalu i izvršite zamjenu:
i odredi njegov predznak. Isplativije je ni ne brojati, već verbalno „procenjivati“. Uzmite, na primjer, tačku koja pripada intervalu i izvršite zamjenu: ![]() .
. 
Dva "plusa" i jedan "minus" daju "minus", dakle, što znači da je izvod negativan na cijelom intervalu.
Akcija, kao što razumijete, mora se izvesti za svaki od šest intervala. Usput, imajte na umu da su faktor brojila i nazivnik striktno pozitivni za bilo koju tačku bilo kojeg intervala, što uvelike pojednostavljuje zadatak.
Dakle, derivat nam je rekao da se SAMA FUNKCIJA povećava za ![]() i smanjuje se za . Pogodno je pričvrstiti intervale iste vrste pomoću ikone spoja.
i smanjuje se za . Pogodno je pričvrstiti intervale iste vrste pomoću ikone spoja.
U trenutku kada funkcija dostigne svoj maksimum:
U trenutku kada funkcija dostigne svoj minimum: ![]()
Razmislite zašto ne možete preračunati drugu vrijednost ;-)
Prilikom prolaska kroz tačku derivacija ne mijenja predznak, pa funkcija tu NEMA EKSTREMA - i smanjila se i ostala u opadanju.
! Ponovimo jednu važnu tačku: tačke se ne smatraju kritičnim - one imaju funkciju nije utvrđeno. Shodno tome, evo ekstremumi u principu ne mogu biti(čak i ako derivacija promijeni predznak).
Odgovori: funkcija se povećava za ![]() i opada na U tački kada je dostignut maksimum funkcije:
i opada na U tački kada je dostignut maksimum funkcije: ![]() , a u tački - minimum: .
, a u tački - minimum: .
Poznavanje intervala monotonosti i ekstrema, zajedno sa utvrđenim asimptote već daje vrlo dobru ideju o izgledu grafa funkcije. Prosječna osoba može verbalno utvrditi da graf funkcije ima dvije vertikalne asimptote i jednu kosu asimptotu. Evo naseg heroja: 
Pokušajte ponovo povezati rezultate studije sa grafikonom ove funkcije.
Ne postoji ekstremum na kritičnoj tački, ali postoji krivulja(što se po pravilu dešava u sličnim slučajevima).
Primjer 4
Pronađite ekstreme funkcije
Primjer 5
Pronađite intervale monotonosti, maksimume i minimume funkcije
... samo neka vrsta praznika X-u-a-cube ispada danas ....
Jaooo, ko je tamo u galeriji ponudio piće za ovo? =)
Svaki zadatak ima svoje suštinske nijanse i tehničke suptilnosti, koje se komentarišu na kraju lekcije.
Funkcije, uopće nije potrebno znati o prisutnosti prve i druge izvedenice i razumjeti njihovo fizičko značenje. Prvo morate razumjeti sljedeće:
- ekstremi funkcije maksimiziraju ili, obrnuto, minimiziraju vrijednost funkcije u proizvoljno malom susjedstvu;
- u tački ekstrema ne bi trebalo biti diskontinuiteta funkcije.
A sada ista stvar, samo jednostavnim riječima. Pogledajte vrh hemijske olovke. Ako je olovka postavljena okomito, s krajem za pisanje prema gore, tada će sama sredina kuglice biti krajnja tačka - najviša tačka. U ovom slučaju govorimo o maksimumu. Sada, ako okrenete olovku s krajem za pisanje prema dolje, tada će na sredini lopte već biti minimum funkcije. Uz pomoć ovdje date slike, možete zamisliti navedene manipulacije za olovku za papir. Dakle, ekstremi funkcije su uvijek kritične tačke: njeni maksimumi ili minimumi. Susedni deo grafikona može biti proizvoljno oštar ili gladak, ali mora postojati sa obe strane, samo u ovom slučaju tačka je ekstrem. Ako je grafikon prisutan samo na jednoj strani, ova tačka neće biti ekstrem čak i ako su uslovi ekstrema ispunjeni na jednoj od njegovih strana. Proučimo sada ekstreme funkcije sa naučne tačke gledišta. Da bi se tačka smatrala ekstremom, potrebno je i dovoljno da:
- prvi izvod je bio jednak nuli ili nije postojao u tački;
- prvi izvod mijenja predznak u ovoj tački.

Uslov se tumači nešto drugačije sa stanovišta derivacija višeg reda: za funkciju diferencibilnu u nekoj tački, dovoljno je da postoji izvod neparnog reda koji nije jednak nuli, dok svi derivati nižeg reda moraju postojati i biti jednaka nuli. Ovo je najjednostavnije tumačenje teorema iz udžbenika, ali za najobičnije ljude, vrijedi objasniti ovu tačku na primjeru. Osnova je obična parabola. Odmah rezervišite, na nultoj tački ima minimum. Samo malo matematike:
- prvi izvod (X 2) | = 2X, za nultu tačku 2X = 0;
- drugi izvod (2X) | = 2, za nultu tačku 2 = 2.

Na tako jednostavan način ilustrirani su uvjeti koji određuju ekstreme funkcije kako za izvode prvog reda tako i za derivate višeg reda. Ovome se može dodati da je drugi izvod upravo isti izvod neparnog reda, nejednak nuli, što je spomenuto malo više. Kada su u pitanju ekstremi funkcije dvije varijable, uvjeti moraju biti ispunjeni za oba argumenta. Kada dođe do generalizacije, tada u igru dolaze parcijalni derivati. Odnosno, neophodno je da postoji ekstremum u tački da su oba izvoda prvog reda jednaka nuli, ili da barem jedan od njih ne postoji. Za dovoljnost prisustva ekstrema istražuje se izraz, koji je razlika između umnoška izvoda drugog reda i kvadrata mješovitog izvoda drugog reda funkcije. Ako je ovaj izraz veći od nule, onda postoji ekstremum, a ako postoji jednakost sa nulom, onda pitanje ostaje otvoreno i potrebno je dodatno istraživanje.