Praktikus munka
matematika
1. Egy függvény határértékének megtalálása. Az első és a második csodálatos határok.
2. Komplex függvény deriváltja. Egy változó függvényének vizsgálata és grafikonok ábrázolása.
3. „A differenciálszámítás alkalmazása a függvények tanulmányozására” teszt.
4. Határozatlan integrálok keresése. Határozott integrálok számítása.
5. Determinánsok számítása.
6. Lineáris egyenletrendszerek megoldása Cramer módszerrel. Teszt.
7. Feladatok megoldása a „Szettek” témában. Logikai algebrai képletek.
8. Véletlenszerű események valószínűségének számítása. Teljes valószínűségi képlet.
9. Numerikus jellemzők számítása.
10. „A valószínűségszámítás és a matematikai statisztika alapjai” teszt
11. Komplex szám trigonometrikus alakja.
12. Műveletek komplex számokkal különböző formában.
MÓDSZERTANI UTASÍTÁSOK MATEMATIKAI GYAKORLATI MUNKÁHOZ
2. TANFOLYAM
A gyakorlati óra az oktatási folyamat olyan szervezési formája, amely során a tanulók egy vagy több gyakorlati munkát végeznek megbízásra és tanári irányítás mellett.
Így a matematika gyakorlati óráin a tanulókban kialakul a problémamegoldó képesség, amelyet a jövőben speciális tudományágak szakmai problémáinak megoldására kell használni.
A gyakorlati munka során a hallgatók elsajátítják az információforrások használatának, a szabályozási dokumentumokkal és oktatóanyagokkal, segédkönyvekkel való munkavégzést, rajzok, diagramok, táblázatok készítését, különféle feladatok megoldását, számításokat.
Matematika gyakorlati órákon megoldandó feladatok:
1) az előadások során megszerzett matematikai elméleti ismeretek bővítése és megszilárdítása;
2) a matematikai problémák sikeres megoldásához szükséges gyakorlati készségek és képességek fejlesztése a tanulókban;
3) a tanulók önképzés iránti igényének fejlesztése, valamint ismeretek és készségek fejlesztése a matematika tanulási folyamatában;
4) kreatív attitűd és kutatási szemlélet kialakítása a matematika tanulási folyamatában;
5) a leendő szakember szakmailag jelentős tulajdonságainak és a megszerzett ismeretek szakmai területen történő alkalmazásának készségeinek kialakítása.
1. sz. gyakorlati óra. Függvényhatárok számítása. Az első és a második csodálatos határok.
Tantárgy : Függvényhatárok számítása.
Cél: alapvető ismeretek elsajátítása a matematika alapvető ágaiban . Az ismeretek asszimilációjának tesztelése a függvényhatárok számításán. Ismételje meg és rendszerezze a témával kapcsolatos ismereteket.
Feladatok:
Kreatív szakmai gondolkodás fejlesztése;
A tudomány nyelvének elsajátítása, a fogalmak működtetésének készsége;
A problémák felállításának és megoldásának készségeinek elsajátítása;
Elméleti és gyakorlati képzés elmélyítése;
A tanulók kezdeményezőkészségének, önállóságának fejlesztése.
Számítástechnikai ismeretek erősítése;
Folytassa a matematikai beszéddel való munkát.
Az önálló munkavégzéshez, a tankönyvvel való munkavégzéshez szükséges készségek kialakítása, az önálló ismeretszerzés készségei;
A fő dolog kiemelésének képességének fejlesztése a szöveggel végzett munka során;
Önálló gondolkodás kialakítása, mentális műveletek: összehasonlítás, elemzés, szintézis, általánosítás, hasonlat;
Mutassa meg a tanulóknak a szisztematikus munka szerepét a tudás elmélyítésében és erősítésében, a feladatok elvégzésének kultúrájában;
A tanulók kreatív képességeinek fejlesztése.
Gyakorlati munka biztosítása:
Módszertani ajánlások elméleti anyaga a gyakorlati munkához.
Matematika, – Sorozat: Középfokú szakképzés. - Rostov-on-Don „Phoenix”, p.
A gyakorlati óra előrehaladása.
1.Az óra témájának megfogalmazása, a téma más tudományági témáival való kapcsolatának magyarázata;
2.A tanulók órára való felkészültségének ellenőrzése;
3. A tényleges óra lebonyolítása a témának megfelelően, a tudományág munkaprogramjának megfelelően:
Tanulmányi elméleti anyagot a „Függvények határainak kiszámítása” témában.
Vegyünk példákat a tipikus feladatok megoldására.
Végezzen önálló munkát a függvények határainak kiszámításán az első és a második figyelemre méltó határérték segítségével.
Válaszold meg a biztonsági kérdéseket.
Elméleti információk és módszertani ajánlások
problémamegoldásról.
1. Elméleti anyag bemutatása.
Egy függvény határértékének kiszámításához egy ponton a következőket kell tennie:
1) Helyettesítsd be az x változó helyett azt, amire x hajlamos.
2) Ha az 1) lépés végrehajtása után bizonytalanságot kapunk https://pandia.ru/text/78/405/images/image003_6.png" width="19" height="22 src=">és cserélje ki a nyíl mínuszjel: (x-a).
3) Ha az 1. lépés végrehajtása után a következő formátumú bizonytalanságot kapjuk: https://pandia.ru/text/78/405/images/image002_13.png" width="18" height="31 src="> A trigonometrikus függvények értékeivel kapcsolatban az első figyelemre méltó határértéket kell használnunk.
Meghatározás. Az első figyelemre méltó határt határnak nevezzük
https://pandia.ru/text/78/405/images/image007_4.png" alt="$\displaystyle \lim_(x\to0)\dfrac(\sin x)(x)=1. $" width="102" height="52">!}
5) Meghatározás:A második figyelemre méltó határ limitnek nevezzük

Az e határérték által adott szám nagyon fontos szerepet játszik mind a matematikai elemzésben, mind a matematika más ágaiban. A számot hívják természetes logaritmus alapja ( https://pandia.ru/text/78/405/images/image009_4.png" alt="$ e$" width="11" height="14">показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:!}
![]()
2. A tanult anyag konszolidációja.
1. példa
https://pandia.ru/text/78/405/images/image015_1.png" width="28" height="30 src=">= -4
Az 1) szabályt használtuk, és behelyettesítettük x helyett azt, amire x-nek törekednie kell, azaz x=2.
2. példa
https://pandia.ru/text/78/405/images/image017_1.png" width="154" height="32 src=">.png" width="21" height="30 src=">= 5
3. példa
https://pandia.ru/text/78/405/images/image021_1.png" width="199" height="37 src=">.png" width="137" height="35 src=">. png" width="138" height="24 src=">=3+3=6
4. példa
https://pandia.ru/text/78/405/images/image004_7.png" width="22" height="31 src=">.png" width="104" height="46 src=">. png" height="30 src=">
5. példa
https://pandia.ru/text/78/405/images/image032_0.png" width="61" height="46 src=">.png" height="30 src=">=2
6. példa
https://pandia.ru/text/78/405/images/image036_0.png" width="18" height="28 src=">
b) 
V) 
3. Az ismeretek, készségek és képességek megszilárdítása.
Végezzen önálló munkát a függvények határainak kiszámításában.
1. sz. gyakorlati munka. 1.opció Számítsa ki a függvény határát: 1. 2. 3. 10. | 1. sz. gyakorlati munka. 2. lehetőség Számítsa ki a függvény határát: 1. 2. 3. 10. |
2. sz. gyakorlati munka.
Tantárgy : Egy függvény deriváltjának megkeresése. Egy változó függvényének vizsgálata és grafikon ábrázolása.
Cél : Tesztelje a gyakorlatban a függvény deriváltja fogalmának ismeretét, elemi függvények deriváltjainak, komplex függvényeknek, inverz függvényeknek a megtalálásának képességét, a derivált táblázat és a differenciálási szabályok segítségével, az összetett és inverz függvény fogalmát, a képességét. hogy egy deriváltot használjunk a függvények tanulmányozásához.
Gyakorlati munka biztosítása:
Tankönyv. "Matematika". – M.: Túzok, 2010.
Matematika. M: Fórum-Infa 2008.
Egyedi kártyák gyakorlati munkavégzési lehetőséggel.
1. Elméleti anyag és példák egy függvény deriváltjának megtalálására.
Meghatározás: Az f(x) (f"(x)) függvény deriváltja az x pontban a függvény növekménye és az argumentum növekménye arányának határa, amikor az argumentum növekménye nullára hajlik:
https://pandia.ru/text/78/405/images/image061_0.png" width="209 height=235" height="235">
A megkülönböztetés szabályai.
Ha az f(x) és g(x) függvényeknek deriváltjai vannak, akkor
2. (u+v)′=u′+v′
3. (uv)′=u′v+v′u
4. (C u)′=C u′, ahol C=állandó
5..png" width="49" height="54 src=">
6. Komplex függvény deriváltja:
f′(g(x))=f′(g) g′(x)
2. Példák.
1..png" width="61" height="41 src=">.png" width="20" height="41 src=">.png" width="20" height="41 src="> .png" width="69" height="41 src=">+4).
A függvény két tényező eredménye: u=https://pandia.ru/text/78/405/images/image071_0.png" width="72" height="41 src=">.png" width=" 64" height="41 src=">.png" width="19" height="41 src=">.png" width="45" height="51 src=">.
A függvény két kifejezés hányadosa: u=https://pandia.ru/text/78/405/images/image079.png" width="52" height="41 src=">..png" width= "215" " height="57 src=">.png" width="197 height=36" height="36">
Megoldás. Keressük meg ennek a függvénynek a deriváltját az összetett függvények differenciálási szabályával (6. képlet):

5. Ha , akkor 
6. y = x 3 – 3x 2 + 5x+ 2. Keressük y "(–1).
y " = 3x 2 – 6x+ 5. Ezért y "(–1) = 14.
7. Ha y= log x kötözősaláta x, Azt y" = (ln x)"kötözősaláta x+ln x(kötözősaláta x) " =1/x∙cos x– ln x bűn x.
Legyen adott függvény. Tanulmányozásához szüksége van:
1) Keresse meg a definíciós tartományát. Ha nem túl nehéz, akkor érdemes megkeresni a tartományt is. (A keresés kérdését azonban sok esetben elhalasztják, amíg a függvény szélső részét meg nem találjuk.)
2) Ismerje meg a függvény általános tulajdonságait, amelyek segítenek a viselkedésének meghatározásában: páros-e vagy páratlan, periodikus-e.
3) Állapítsa meg, hogyan viselkedik a függvény, amikor az argumentum megközelíti a definíciós tartomány határpontjait, ha vannak ilyen határpontok. Ha egy függvénynek vannak megszakadási pontjai, akkor ezeket a pontokat is ellenőrizni kell a függvény függőleges aszimptotáinak megléte szempontjából. Keresse meg a ferde aszimptotákat.
4) Keresse meg a gráf koordinátatengelyekkel való metszéspontjait, ami abból áll, hogy egyszerűen kiszámítjuk a függvény értékét a feltétel mellett:
OX tengellyel: y=0;
OY tengellyel: x=0.
A tengellyel való metszéspontok megtalálása egy összetett algebrai egyenlet megoldásához vezethet, ami talán csak megközelítőleg megoldható. Miután megtaláltuk a függvény gyökereit és a folytonossági pontokat, meghatározhatjuk a függvény előjelét az egyes pontok közötti intervallumokban. Ez megtehető a függvény értékének az intervallum bármely pontján történő kiszámításával, vagy az intervallum módszerrel.
5) Keresse meg a monotonitás intervallumait. Ehhez keresse meg a deriváltot, és oldja meg az egyenlőtlenséget:
https://pandia.ru/text/78/405/images/image089.png" width="49" height="19 src=">, a funkció csökken.
A monotonitás intervallumainak megtalálása után azonnal meghatározhatjuk a lokális szélsőség pontjait: ahol a növekedést csökkenés váltja fel, ott a lokális maximumok, ahol a csökkenés helyére növekedés lép fel, ott a lokális minimumok találhatók.
6) A konvexitás és konkávitás intervallumainak megtalálása a második derivált..png" width="39" height="19 src="> segítségével történik az intervallumokon:
ha https://pandia.ru/text/78/405/images/image090.png" width="39" height="19 src=">‹0, akkor a függvénygráf görbe konvex.
Ugyanakkor az inflexiós pontokat úgy definiáljuk, mint azokat a pontokat, ahol a függvény a konvexitás irányát megváltoztatja (és folytonos).
7) A gráf metszéspontjainak megtalálása az aszimptotával és a további pontokkal. Ez a pont nem kötelező, de az ilyen pontok megtalálása teljessé és teljessé teszi a függvény és grafikonjának tanulmányozását.
Megjegyzendő, hogy a rajzon a függvények tanulmányozása során kapott pontokat hasznos azonnal ábrázolni a koordinátatengelyeken és a grafikonon. Ez segít megérteni a grafikon megjelenését az út során.
3. Csináld magad:
|
választási lehetőség | Keresse meg az y függvény deriváltját: |
választási lehetőség | Keresse meg az y függvény deriváltját: |
1.y=6- | 1. y=-6- 5.y= |
||
1. y=-7-1 | 1. y=-7-1 |
||
1.y=4x-3tgx+6x-8 | 1.y=-5x+2ctgx+3x-2 |
||
Az óra céljai:
Nevelési- ismerni a differenciálási képleteket; differenciálási szabályok;
komplex függvény differenciálása; származék fizikai és geometriai jelentése;
függvény grafikonjának érintőjének egyenlete.
Fejlesztő - tudjon függvények származékait megtalálni; problémák megoldása fizikai jelentés, geometriai jelentés felhasználásával; keresse meg egy függvény deriváltjának értékét egy pontban; matematikailag helyesen magyarázza és indokolja az elvégzett cselekvéseket.
Oktatási – fejleszteni a függetlenséget, a felelősséget, a reflexiót.
Az órák alatt
I. Szervezési mozzanat.
II. Házi feladat ellenőrzése
(a szünetekben a konzulensek ellenőrzik (diákok) és osztályzatokat adnak).
III. Célkitűzés és motiváció
A tanár tájékoztatja a tanulókat, hogy ez a lecke az utolsó lecke a „Származékok számítása” témában, és felkéri őket, hogy fogalmazzák meg saját céljaikat.
Tanár: „A nagy filozófus, Konfuciusz egyszer azt mondta: „Három út vezet a tudáshoz: az elmélkedés útja a legnemesebb út, az utánzás útja a legkönnyebb út, és a tapasztalat útja a legkeserűbb út.” Tehát ma az órán mindenki eldönti, hogy e témával kapcsolatos tudáshoz melyik úton jár.”
A tanulók azt a feladatot kapják, hogy mutassák be tudásukat és készségeiket a deriváltak kiszámításában, és kapnak egy óratervet.
I. szakasz: A feladat végrehajtása az „Emlékezz” kártya segítségével.
(képletek és differenciálási szabályok ismeretének tesztelése).
II. szakasz: Szóbeli frontális munka az ismeretek ismétléséről és általánosításáról.
III. szakasz:„Tesztelőrejelzés” (a feladat elvégzése során a tanácsadók segítsége elfogadható).
énV. szakasz: Egy gyakorlati probléma megoldása.
V. szakasz:Önálló munkavégzés
A munka és a házi feladat I., III., V. szakaszát értékelik. A tanácsadók ellenőrzik és beírják az eredményeket az értékelő táblázatba.
Értékelési szempontok: "5"- 19-20 pont;
"4"- 15-18 pont;
"3"- 10-14 pont.
A tudáshoz vezető utak
- A referencia ismeretek sokszorosítása, javítása
I. szakasz.
Cél: a képletek és a megkülönböztetési szabályok ismeretének kontrollja, önkontrollja
Emlékezik! F.I. _______________________________________________________ |
|
Derivált |
|
c,c - cons t |
|
|
|
|
|
f"(x)+ g"(x) |
|
f(x)* g(x) |
|
|
|
A feladat végén öntesztet hajtunk végre a „Származékok táblázata” segítségével. A kártyákat ellenőrzésre átadjuk tanácsadóknak (a kártyákon nem végezhető javítások).
V. Az ismeretek általánosítása és rendszerezése
szakasz II.
1. Szóbeli frontális munka.
A. Generáljon feladatot ehhez a feltételhez, és oldja meg.
![]()
1. Határozza meg a függvény deriváltjának értékét a t = 3 pontban. (Válasz: 21.)
2. Készítsen egyenletet a függvény grafikonjának érintőjére a t = 3 pontban. (Válasz: y = 21x-45.).
3. Határozza meg a test sebességét és gyorsulását t=3c pillanatban, ha a mozgás törvénye a képlettel adott! (Válasz: 21 m/s, 16 m/s²).
4. Határozza meg a függvény grafikonjára húzott érintő szögegyütthatóját a t = 3 pontban. (Válasz: 21.).
5. Határozza meg a függvény grafikonjának érintőjének dőlésszögének érintőjét a t = 3 pontban, és határozza meg az érintő és az Ox tengely pozitív iránya közötti szög típusát! (Válasz: tgα, az α szög hegyes)
B. Keresse meg a függvények deriváltjait

2. szakasz III„Tesztelőrejelzés”


A feladat végén a végső válaszok alapján öntesztet hajtanak végre, és a teszteket átadják tanácsadóknak. (a kártyákon a javítások nem megengedettek).
Válaszok:
1 lehetőség |
||||
2. lehetőség |
- A probléma megoldása
énV. szakasz
Egy emelt szintű probléma frontális megoldása (a megoldást tanácsadók végzik az osztállyal együtt).
Feladat
Milyen paraméterértékeken a egy függvény grafikonjának érintői ![]()
az X tengellyel való metszéspontjaiban 60°-os szöget zárnak be egymással?

A grafikon egy parabola, amelynek felfelé ágai két pontban metszik az X tengelyt (az eset a=0 nem felel meg a probléma értelmének):
IX. Összegzés és osztályozás
1. Kérdések: a) Megvalósult-e az óra célja?
b) Melyik szakasz tűnt a legnehezebbnek?
c) Mi volt a legérdekesebb?
2. A tanácsadók kihirdetik az eredményeket (az úton lévő tanulók száma és neve
utánzás, reflexió és tapasztalati módok).
Gyakorlati lecke
Tantárgy: Származékok keresése. A derivált alkalmazása függvények tanulmányozására és grafikonok ábrázolására.
Cél: Sajátítsa el a deriváltak számítását, tanuljon meg egy függvényt a derivált segítségével felfedezni
Az oktatás eszközei: jegyzetfüzetek gyakorlati feladatokhoz, prezentációk a témában, internetes források.
1. Tekintse meg elméleti anyagát a következő témákban: „Derivatalszámítási szabályok”, „Függvény szélsőértéke”, „Konvexitás, homorúság. Inflexiós pont."
2. Tekintse át a feladatok mintáit.
3. Végezze el az 1. számú tesztfeladatot!
Ellenőrző kérdések:
1. Határozza meg egy függvény maximumát (minimumát) egy pontban. Mit mondhatunk a függvény növekményének előjeléről a maximum (minimum) pont meglehetősen kis környezetében?
2. Mik a szükséges feltételek egy függvény szélsőértéke létezéséhez? Mi a geometriai jelentésük?
3. Mi a szabály a függvény legnagyobb és legkisebb értékének megtalálására egy szegmensen?
4. Határozza meg egy görbe konvexitását (konkávságát) egy intervallumon.
5. Mi a szabály a görbe konvexitási és konkávsági intervallumainak meghatározására?
6. A görbe inflexiós pontja. Hogyan lehet megtalálni őt?
7. Mi az algoritmus egy függvény gráfjának elkészítéséhez?
A derivatívák kiszámításának szabályai
Komplex függvény származéka.
Ha nál nél=ƒ( És), u=φ(x), akkor nál nél¢ ( x)=ƒ¢ (i)·φ¢ (x).
Egy összeg származéka.
Ha nál nél(x)=És(x)+v (x), Ez nál nél¢ (x)=És¢ (x)+v ¢ (x)
A termék származéka.
Ha y(x)=u(x)· v (x), Ez nál nél¢ = És¢ · v + u · v ¢ .
Különösen, ( Val vel· És)¢ =c· És¢, azaz a konstans tényező kikerül a származékjel alól. Ezt könnyű ellenőrizni
(u 2 ) ¢ = 2 u u ¢ , (u 3 ) ¢ =3u 2 u ¢ , … , (u n ) ¢ =n·u n–1 u ¢ .
A hányados származéka.
Ha akkor  .
.
Származékos táblázat
1. (Val vel)¢ =0
Összetett függvény esetén: ha u=u(x), Ez:
2. (X)¢ =1
3. (X α )¢ = α · xα–1, A– bármilyen valós szám.
 .
.
3. 

4. (A x ) ¢ =a x · ln A
4. 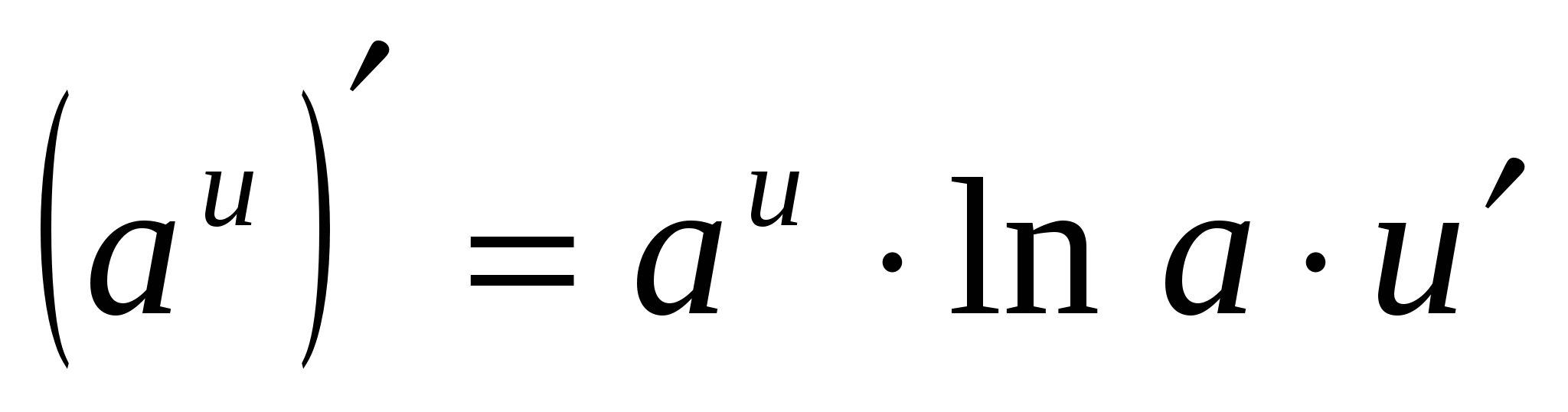

5. (log
a
x)
¢
=
 .
.
5. 

6. (bűn x)¢ =cos x
6. 
7. (cos x)¢ = –sin x
7. 
8. (tg x)¢
=
8. 
9. (ctg x)¢
=
9. 
10. 
10. 
11. 
11. 
12. 
12. 
13. 
13. 
Tekintse át a példákat
1. példa
y=(3–2 sin 5x ) 4 | Származtatott képleteket alkalmazunk a És α ,bűn u |
y ¢ =4·(3–2·sin5x) 3·(3–2sin5x) ¢ =4·(3–2·sin5x) 3 ·(0–2·cos5x·5) = –40·(3–2·sin5x) 3 .
2. példa
. 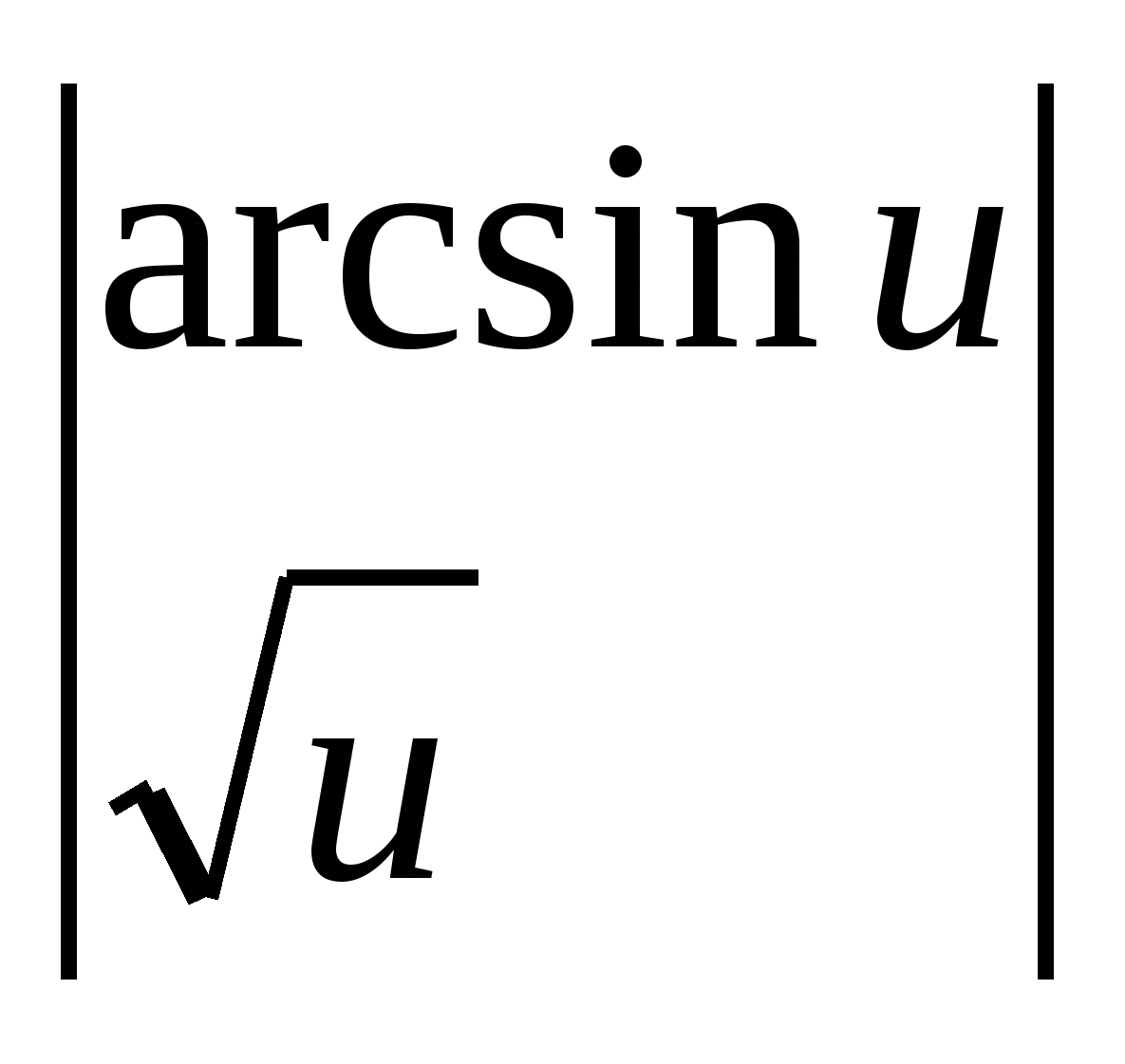

3. példa
 .
. 

4. példa



5. példa.
 .
. 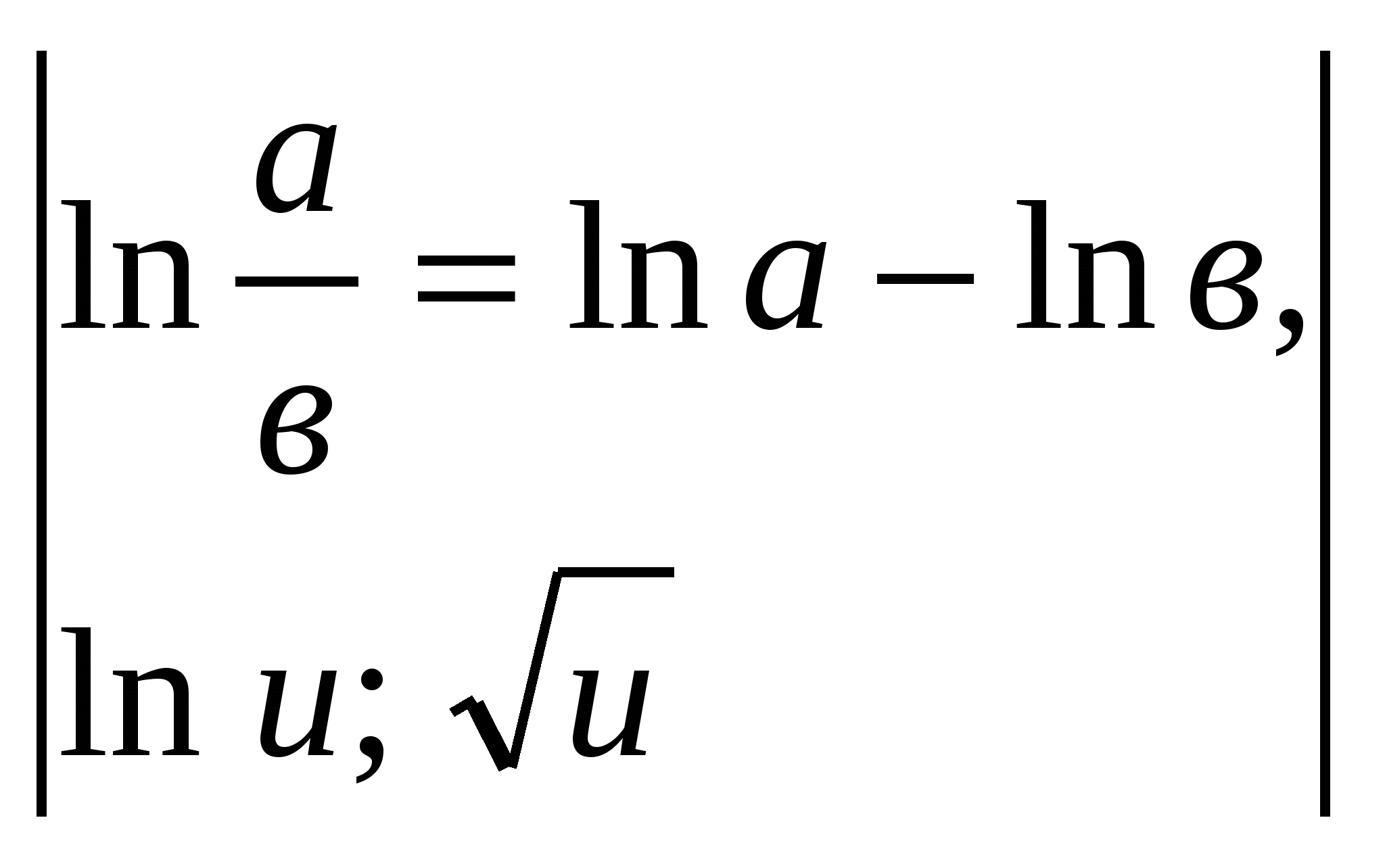

A függvény szélsőértéke
Az egyik szélsőértékben lévő függvény vizsgálata a deriváltak egyik legfontosabb alkalmazása. Nézzük meg a minimumok és maximumok meghatározását, és hogyan találhatjuk meg őket.
Legyen a ƒ( x) meghatározott és differenciálható egy bizonyos halmazon és egy ponton x A 0 egy pont benne.
Meghatározás. Funkció ƒ (x) pontban x 0 rendelkezik maximális(minimum), ha van ilyen környéke a pontnak x 0, ami mindenkinek szól x erről a területről ƒ (x) < ƒ (x 0 ) (ƒ (x) > ƒ (x 0 )).
Pont x A 0-t ekkor pontnak nevezzük maximális(minimális).

Rizs. 1.
Egy olyan függvény grafikonja látható, amelynek két maximális pontja van ( x 1 és x 3) és két minimum pont ( x 2 és x 4), és a maximális érték kisebb lehet, mint a minimum ( ƒ (x 1 ) < ƒ (x 4)). Ez hangsúlyozza azt a tényt, hogy egy függvény szingularitását csak egy bizonyos pont közelében jellemezzük.
A függvény értékeit a maximum és minimum pontokon szélsőséges értékeknek, ill szélsőségek. A fenti grafikon azt mutatja, hogy a szélsőpontok ( x 1 , x 2 , x 3 , x 4) határozza meg a függvény monotonitási intervallumait, amelyek mindegyikében a derivált megtart egy bizonyos előjelet. A szélsőpontoknál természetesen a derivált nullára megy. Fogalmazzunk meg egy tételt arról szükséges feltétel szélsőség megléte.
Tétel. Ha a funkció ƒ (x) pontban x 0-nak szélsőértéke van, akkor a függvény deriváltja ezen a ponton egyenlő nullával, azaz ƒ¢ ( x 0)=0.
Rögtön jegyezzük meg, hogy ez a feltétel nem elégséges, vagyis a fordított állítás nem mindig igaz. Az egyenlőségtől ƒ ¢ ( x 0)= A 0 nem feltétlenül jelenti azt a ponton x 0 van egy szélsőség.
Ezt megerősíti a függvény példája ƒ (x)=x 3 .
meg fogjuk találni ƒ ¢ ( x)= 3x 2 . Azon a ponton x=0 ƒ ¢ (0)=0 . De olyan közel a lényeghez, amennyire csak akarja x=0 meg fogjuk találni x> 0, hol ƒ (x)=x 3 > 0, meg fogjuk találni x< 0, где ¦ (x)=x 3 < 0. Т. е. не существует какая-либо малая окрестность точки x=0, ahol minden x függvény értéke egy pontban x=0 lesz a legnagyobb vagy a legkisebb. Ezért pont x A =0 nem szélsőpont.
Lehet másképp vitatkozni. Mivel a származék ƒ ¢ (x) = 3x 2 , majd a függvény ƒ(x)=x 3 bármely valós x esetén növekszik, és nincs szélsőértéke.
Pontok, ahol a szükséges szélsőfeltétel teljesül (ƒ ¢ (x)=0) hívják kritikai .
Nyilvánvalóan a függvény grafikonjának érintője azokban a pontokban, ahol ƒ ¢ (x)=0, párhuzamos az x tengellyel Ox .
Elegendő állapot extrémum a következő tételekben van megadva.
1. tétel. Ha x A 0 a függvény kritikus pontja, amelyen áthaladva a derivált előjelet vált, ekkor x A 0 egy szélsőpont, vagyis ha a derivált előjelet változtat pluszról mínuszra, akkor az maximum pont, ha pedig mínuszról pluszra, akkor minimum pont.
Figyeljük meg, hogy nincs szélsőérték egy pontban, ha a derivált nem változtat előjelet. Az iskolai kurzusból ismert az extrémum első származékot használó tanulmányozásának szabálya. Néha célszerűbb egy szélsőséghez elegendő feltételt megfogalmazni a második származék használatával.
Legyen a ƒ( x) kétszer differenciálható bizonyos tartományokban (azaz ƒ( x) van ƒ¢ ( x) És ƒ ¢¢ ( x)).
2. tétel. Ha x 0 – a függvény kritikus pontja ƒ(x)és ƒ ¢¢ (X 0 ) > 0 , Azt x 0 – minimum pont, ha ƒ ¢¢ (X 0 ) < 0, то x 0 – maximum pont.
A második derivált segítségével meghatározzuk egy függvény grafikonjának konvexitását vagy konkavitását.
Konvexitás, homorúság. Inflexiós pont.
Ív y=ƒ(x) nak, nek hívják domborúanth lent bármelyikét tangens
ƒ ¢¢ ( x) < 0.
Ív y=ƒ(x) nak, nek hívják homorú intervallumon, ha a görbe minden pontja fekszik magasabb bármelyikét tangens ezen az intervallumon. Aztán ezen az intervallumon
ƒ ¢¢(x) > 0
Meghatározás. Inflexiós pont a görbe egy olyan pont, ahol a görbe egyik oldalán konvex, a másikon homorú.
Az inflexiós pontban ƒ ¢¢ ( x)=0.
Tehát a második derivált előjele (valamint magának a függvénynek és annak első deriváltjának előjele) jelzi a függvénygráf jellemzőit. Nézzük őket újra.
Ha mindenkinek x az intervallumon ( A, b) ƒ (x) > 0 (ƒ (x) < 0), akkor a grafikon az x tengely felett (alatt) helyezkedik el.
Ha mindenkinek x az intervallumon ( A, b) ƒ ¢ ( x) > 0 (ƒ ¢ ( x) < 0), то функция на (A, b) növekszik (csökken).
Ha mindenkinek x az intervallumon ( A, b) ƒ ¢¢ ( x) > 0 (ƒ ¢¢ ( x) < 0), то график на (A, b) homorú (domború).
ƒ( x A )=0 a függvény „nullapontjait”, azaz a gráf Ox tengellyel való metszéspontjait határozza meg.
Az egyenlet ƒ ¢ ( x)=0 a kritikus pontokat határozza meg.
Az egyenlet ƒ ¢¢ ( x A )=0 a lehetséges inflexiós pontokat határozza meg.
Funkcióvizsgálati séma
A függvény tanulmányozására ƒ (x) és az ábrázolás y=ƒ(x) kell találni:
1) a függvény definíciós tartománya és a gráf és a koordinátatengelyek metszéspontja;
2) a monotónia intervallumai;
3) szélsőpontok és függvényértékek ezeken a pontokon;
4) a gráf konvexitási és konkávsági intervallumai;
5) a gráf inflexiós pontjai;
6) Szerkessze meg derékszögű koordinátarendszerben az összes kapott pontot (néha a gráf tisztázása érdekében további pontokat kapunk) és magát a gráfot.
Egy függvény legkisebb és legnagyobb értéke egy szegmensen
Az optimalizálási módszer egyes problémáinak megoldása során fontos, hogy egy adott szegmensen meg tudjuk találni egy függvény legkisebb vagy legnagyobb értékét. A függvény ezeket az értékeket a kritikus pontokon vagy a szegmens végén éri el.
Keresési séma a függvény legkisebb és legnagyobb értéke ƒ (x) a szegmensen [ A, b].
1. Keresse meg a függvény deriváltját! ƒ ¢ ( x).
2. Keresse meg az egyenlet kritikus pontjait! ƒ ¢ ( x)=0.
3. Válassza ki azokat a kritikus pontokat, amelyek ehhez a szegmenshez tartoznak [ A, b], és keresse meg a függvény értékét ƒ (x) minden ilyen ponton.
4. Számítsa ki a függvényértékeket ƒ (x) a szegmens végén: ƒ( A) és ƒ( b).
5. A kapott függvényértékek közül válassza ki a legnagyobbat (legnagyobb) és a legkisebbet (legkisebbet).
2. példa
Keresse meg egy függvény legnagyobb és legkisebb értékét ƒ(x)=x 3 -9x 2 +24х–10 a szegmensen.
1. ƒ ¢ ( x)= 3x 2 – 9·2 x 2 + 24.
2. ƒ ¢ ( x)=0, 3(x 2 –6x+8)=0, x 1 =2, x 2 =4.
3. Az x 2 =4 pont nem tartozik a szakaszhoz. Ezért a függvény értékét csak a pontban számítjuk ki x 1 =2
ƒ(2)=2 3 –9·2 2 +24·2–10=10.
4. Funkcióértékek a szakasz végén: ƒ(0)= –10, ƒ(3)=3 3 –9·3 2 +24·3–10, ƒ(3)=8.
5. Megszerzett értékek:
ƒ(2)=10, ƒ(0)= –10, ƒ(3)=8.
A legmagasabb érték 10, és a ponton érjük el x=2. A legkisebb értéke –10, és a ponton érhető el x=0.
3. példa
Határozza meg a görbe konvexitási és homorúsági és inflexiós pontjait! y=x+36x 2 –2x 3 –x 4 .
Ennek a függvénynek a definíciós tartománya az összes valós szám halmaza, azaz. xЄ(–∞, +∞).
Keressük a második származékot.
nál nél¢ =1+72 x–6x 2 –4x 3 .
nál nél¢¢ =72–12 x–12x 2 = –12(x 2 +x–6).
Az Eq. nál nél¢¢ =0 megkapjuk az inflexiós pont abszcisszáját:
–12(x 2 +x–6)=0 x 1 = –3; x 2 =2.
Határozzuk meg a jelet nál nél¢¢ időközönként
(–∞; –3), (–3; 2), (2, +∞).
x
(–∞, –3)
(–3; 2)
(2; +∞)
nál nél¢¢
görbe alakja
konvex
inflexió
homorú
inflexió
konvex
Keressük meg az inflexiós pontok ordinátáit:
nál nél(–3)=726; M 1 (–3; 726) – inflexiós pont
nál nél(2)=114; M 2 (2; 114) – inflexiós pont.
A (–3; 2) intervallumon a görbe homorú. A (–∞; –3) és (2; +∞) intervallumokon – konvex.
Minták a feladatokból
1. számú feladat.
Keresse meg a függvény töréspontjait, és ábrázolja a grafikont

Funkció ƒ (x) minden valósra van definiálva xés folyamatos a jelzett intervallumok mindegyikén: (–∞; –1), [–1; 0], (0, +∞). Vizsgáljuk meg a funkciót ƒ (x) pontok folytonossága érdekében x= –1 és x=0.
Ehhez mindegyik ponton egyoldalú határértékeket fogunk találni.

Mivel az egyoldalú korlátok eltérőek, akkor x = –1 – az első típusú szakadási pont.

Az egyoldali határértékek egyenlőek, azaz az x=0 pontban van a függvény határértéke és 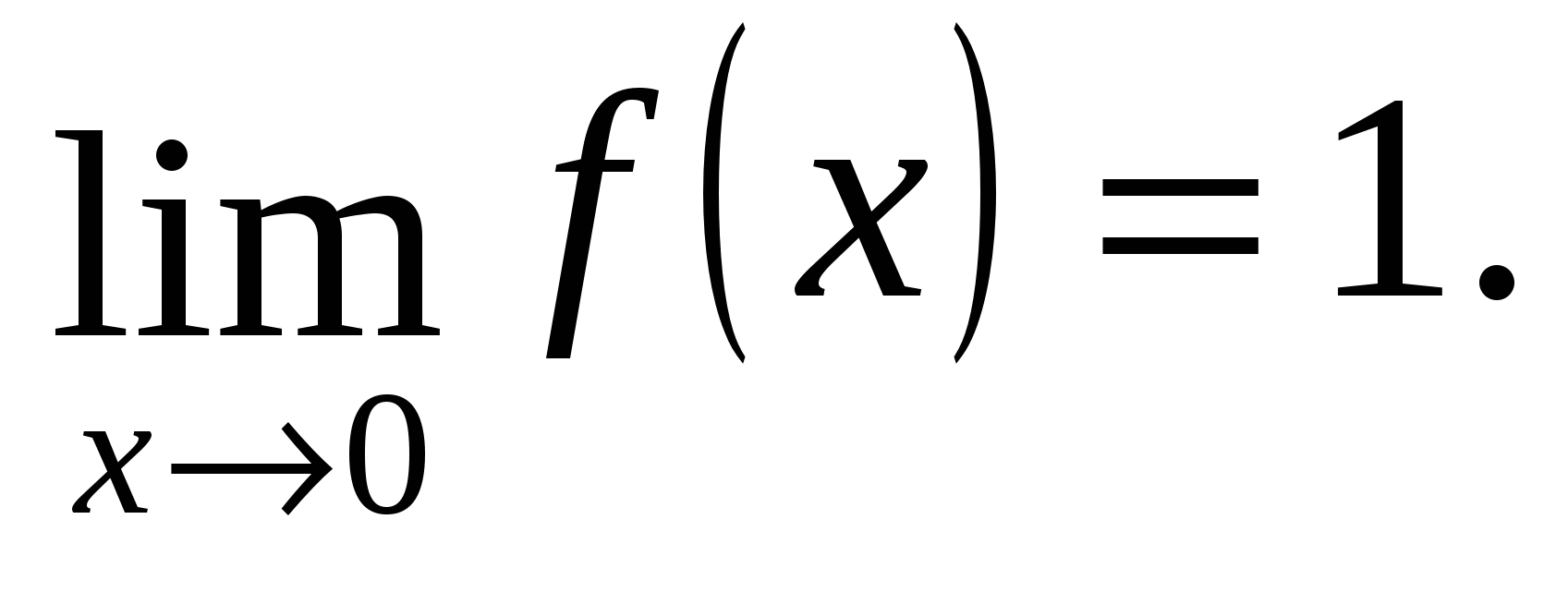
Hasonlítsuk össze ezt a határértéket a függvény értékével a pontban: 
Mert  majd be x=0-nál az ƒ(x) függvény folytonos.
majd be x=0-nál az ƒ(x) függvény folytonos.
Ábrázoljuk a ƒ függvényt (X), tekintettel arra
1)  – egy egyenes egyenlete,
– egy egyenes egyenlete,
2)  – a felső félkör egyenlete
– a felső félkör egyenlete  az origó középpontjával és a sugárral egyenlő egységgel, és a –1 £ feltétellel x 0 £ egyenlet
az origó középpontjával és a sugárral egyenlő egységgel, és a –1 £ feltétellel x 0 £ egyenlet  negyedkört határoz meg.
negyedkört határoz meg.
3) számára x > 0 a grafikont az egyenlet adja  . Az egyenletből megtaláljuk ennek a görbének az Ox tengellyel való metszéspontjait
. Az egyenletből megtaláljuk ennek a görbének az Ox tengellyel való metszéspontjait  x > 0 esetén. x= π
n, Ahol n
=1, 2, 3, 4,
x > 0 esetén. x= π
n, Ahol n
=1, 2, 3, 4,

Rizs. 2.
2. feladat.
Írjon egyenleteket egy egyenes érintőire!  pontokon, ahol x=0 és x=4. Keresse meg az érintők metszéspontját és a köztük lévő szöget! Készítsen rajzot.
pontokon, ahol x=0 és x=4. Keresse meg az érintők metszéspontját és a köztük lévő szöget! Készítsen rajzot.
Egy egyenes érintőjének egyenlete y=ƒ(x)úgy néz ki, mint a
Ahol nál nél 0 =ƒ( x 0).
Azon a ponton x=0 nál nél(0)=ƒ(0)=5.
nál nél¢ =ƒ ¢ (X)=x–3 ƒ¢ (0)= –3.
M 1 (0, 5) alakja van y- 5= –3(x–0) vagy
y= –3x+5.
Azon a ponton x=4 nál nél(4)=ƒ(4)=1. ƒ¢ (4)=4–3=1.
Érintő egyenlete egy pontban M 2 (4, 1) alakja van y- 1=x–4 ill
y=x–3.
Az érintők metszéspontját a rendszer megoldásával kapjuk meg

Metszéspont M 3 (2, –1).
Sarok φ érintők között a képletből megtaláljuk:
 ,
,
Ahol k 1 = –3; k 2 =1 – érintők szögegyütthatói.
 .
.
Sarok φ =arctg 2.
Építsük meg ezt a vonalat  – egy parabola, amelynek csúcsa abban a pontban van, ahol x=3, mert nál nél¢
=0 at x=3. meg fogjuk találni
– egy parabola, amelynek csúcsa abban a pontban van, ahol x=3, mert nál nél¢
=0 at x=3. meg fogjuk találni  . Pont M 4 (3;
. Pont M 4 (3;  ) a parabola csúcsa.
) a parabola csúcsa.
R 
van. 3.
3. feladat.
Funkció felfedezése  és kirajzolódik.
és kirajzolódik.
1. Ez a függvény egy polinom (a zárójeleket kinyithatod, harmadfokú polinomot kapunk), ezért definiált, folytonos és tetszőlegesre differenciálható x.
2. Keressük a deriváltot.
 .
.
Az Eq. nál nél¢ =0 keressük meg a kritikus pontokat: 3 x·( x–2)=0, x 1 =0, x 2 =2.
Fedezzük fel őket.
x
(–∞, 0)
(0; 2)
(2; +∞)
nál nél ¢
nál nél
3. Tehát a függvény a (–∞, 0) és (2, +∞) intervallumon növekszik, a (0; 2) intervallumon csökken, maximuma x=0-nál, minimuma x=2-nél van:
nál nél max = nál nél(0)=4; nál nél min = nál nél(2)=0.
4. Keressük a második deriváltot.
nál nél¢¢ = 6·( x-1).
A görbe hol domború nál nél¢¢ < 0, т. е. 6·(x–1) < 0, x < 1.
A görbe hol homorú nál nél¢¢ > 0, azaz x > 1.
Tehát a (–∞, 1) intervallumon a görbe konvex; az (1, +∞) intervallumon pedig homorú.
5. Az egyenletből megtaláljuk az inflexiós pontot nál nél¢¢ =0. És így, x=1 – az inflexiós pont abszcisszája, mert ez a pont választja el a görbe konvexitási és homorúsági intervallumait. Inflexiós pont ordinátája: nál nél(1)=2.
Egy függvény grafikonja nál nél=(x+1)·( x–2) 2 pontban metszi az Ox tengelyt nál nél=0, azaz mikor x= –1 és x=2;
pontnál keresztezi az Oy tengelyt x=0, azaz mikor nál nél=4. Három pontot kaptunk: (–1; 0), (2; 0), (0; 4). Az összes kapott pontot beírjuk a táblázatba, hozzáadva a szomszédos pontokat.
–2
–1



–16


van. 4 y=(x+1)(x–2) görbe 2.
1. számú feladat
Olyan feladatokat mutatunk be, amelyekben lehet egy, kettő, három vagy több helyes válasz. Karikázd be az összes helyes válasz számát!
1. Ha  majd a függvény
majd a függvény
1) növekszik
2) csökkenő
3) állandó
2. Ha
1) Növekvő
2) Csökkenő
3. Ha  , majd a függvény
, majd a függvény
1) Növekvő
2) Csökkenő
4. Ha  , majd a függvény
, majd a függvény
1) Növekvő 3) Csökkenő
2) Állandó 4) Monoton
5. Funkció  Is
Is
1) Méghozzá
2) Még csak nem is
3) se nem páros, se nem páratlan
4) Időszakos
5) Nem időszakos
6) Trigonometrikus
7) Elemi
6. Funkció  Is
Is
1) akár
2) páratlan
3) se nem páros, se nem páratlan
4) időszakos
5) nem időszakos
6) trigonometrikus
7) elemi
2) Weierstrass 4) Dirichlet 6) Leibniz
8) Megoldás  Egyenletek
Egyenletek
1) 0 3) 0 és 3 5) 2 7) 3
2) 2 és 3 4) 2 6) -5 és 1 8) 5 és 1
9) az egyenlőtlenség megoldása 
1) ( ; 1) 3) (
; 1) 3) ( ; 1) 5) (-
; 1) 5) (- ;1)
;1)
2) (1; 5) 4) (2;  ) 6)
) 6) 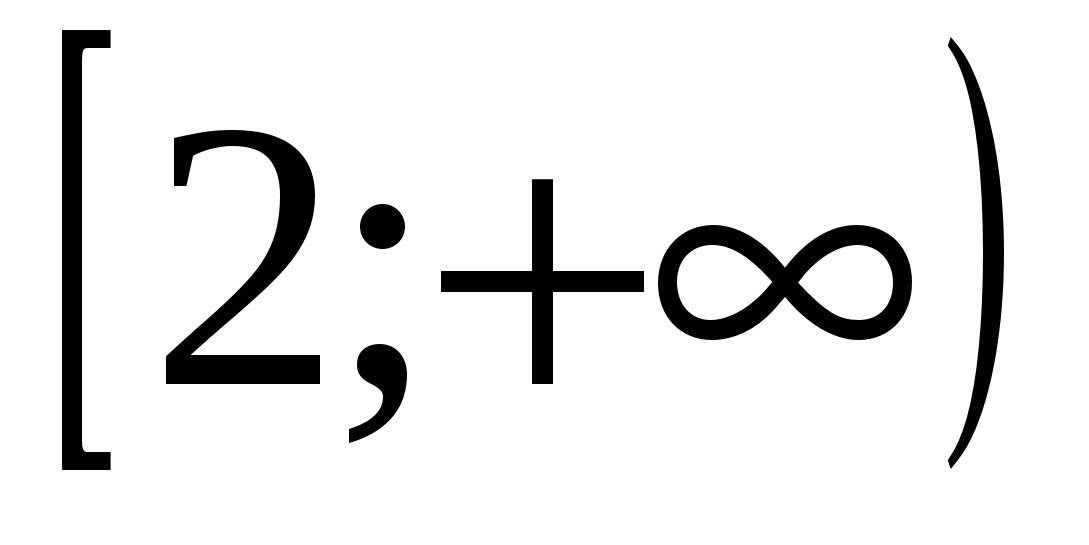
10) Módszer  Az összeg megtalálható
Az összeg megtalálható
1) vektorok
2) egyenes
3) szegmens
11) Ha  , majd a függvény
, majd a függvény
1) Homorú 3) Konvex 5) Csökkenő
2) Monoton 4) Növekvő 6) Állandó
12) a függvény definíciós tartománya egyenlő 
1) ( ;0)
;0)
2) (0;  )
)
3) (- ;
; )
)
4) (0;1)
5) 
6) 
7) (-1;1)
8) 
9) 
13) funkció  van
van
1) tájékoztató jellegű
2) trigonometrikus
3) hatalom
4) logaritmikus
14) ha y = függvények x  akkor ő az
akkor ő az 
1) akár
2) páratlan
3) se nem páros, se nem páratlan
15) funkció  nál nél
nál nél  van
van

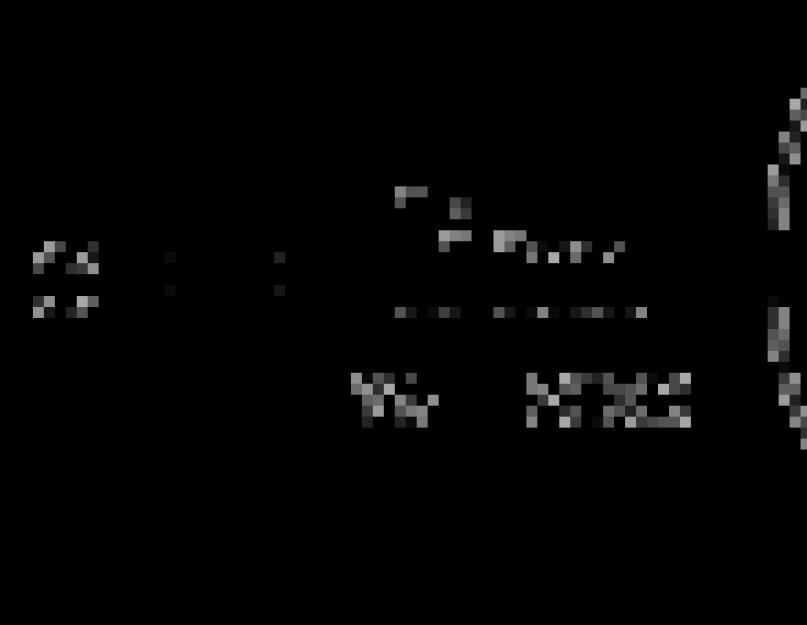
 .
.



