Praktinis darbas
matematikos
1. Funkcijos ribos radimas. Pirmasis ir antrasis yra nuostabios ribos.
2. Sudėtinės funkcijos išvestinė. Vieno kintamojo funkcijos tyrimas ir grafikų braižymas.
3. Testas „Diferencialinio skaičiavimo taikymas funkcijoms tirti“.
4. Neapibrėžtinių integralų radimas. Apibrėžtųjų integralų skaičiavimas.
5. Determinantų skaičiavimas.
6. Tiesinių lygčių sistemų sprendimas Cramerio metodu. Testas.
7. Užduočių sprendimas tema „Aibiniai“. Loginės algebros formulės.
8. Atsitiktinių įvykių tikimybių skaičiavimas. Bendrosios tikimybės formulė.
9. Skaitinių charakteristikų skaičiavimas.
10. Testas „Tikimybių teorijos ir matematinės statistikos pagrindai“
11. Sudėtinio skaičiaus trigonometrinė forma.
12. Veiksmai su kompleksiniais skaičiais įvairiomis formomis.
MATEMATIKOS PRAKTINIO DARBO METODINIAI NURODYMAI
2 KURSAS
Praktinė pamoka – tai ugdymo proceso organizavimo forma, kai mokiniai pagal užduotį ir vadovaujami mokytojo atlieka vieną ar kelis praktinius darbus.
Taigi praktiniuose matematikos užsiėmimuose mokiniai ugdo gebėjimus spręsti uždavinius, kuriuos ateityje reikėtų panaudoti sprendžiant specialiųjų disciplinų profesines problemas.
Praktinio darbo metu studentai įvaldo gebėjimą naudotis informacijos šaltiniais, dirbti su norminiais dokumentais ir mokymo medžiaga, žinynais, sudaryti brėžinius, diagramas, lenteles, spręsti įvairius uždavinius, atlikti skaičiavimus.
Uždaviniai, kurie sprendžiami per matematikos praktines pamokas:
1) paskaitų metu įgytų matematikos teorinių žinių plėtimas ir įtvirtinimas;
2) ugdyti mokiniuose praktinius įgūdžius ir gebėjimus, reikalingus sėkmingai spręsti matematikos uždavinius;
3) mokinių savišvietos poreikio ugdymas ir žinių bei gebėjimų tobulinimas matematikos studijų procese;
4) kūrybinio požiūrio ir tiriamojo požiūrio formavimas matematikos studijų procese;
5) būsimojo specialisto profesiniu požiūriu reikšmingų savybių ir įgūdžių pritaikyti įgytas žinias profesinėje srityje formavimas.
Praktinė pamoka Nr.1. Funkcijos ribų skaičiavimas. Pirmasis ir antrasis yra nuostabios ribos.
Tema : Funkcijos ribų skaičiavimas.
Tikslas: pagrindinių žinių įgijimas pagrindinių matematikos šakų srityje . Žinių įsisavinimo tikrinimas skaičiuojant funkcijų ribas. Pakartokite ir susisteminkite žinias šia tema.
Užduotys:
Kūrybinio profesinio mąstymo ugdymas;
Mokslo kalbos įvaldymas, sąvokų veikimo įgūdžiai;
Įvaldyti problemų nustatymo ir sprendimo įgūdžius;
Gilinamasis teorinis ir praktinis mokymas;
Mokinių iniciatyvumo ir savarankiškumo ugdymas.
Skaičiavimo įgūdžių stiprinimas;
Tęskite darbą su matematine kalba.
Savarankiško darbo, darbo su vadovėliu įgūdžių formavimas, savarankiško žinių įgijimo įgūdžiai;
Gebėjimo pabrėžti pagrindinį dalyką dirbant su tekstu ugdymas;
Savarankiško mąstymo formavimas, protinės operacijos: palyginimas, analizė, sintezė, apibendrinimas, analogija;
Parodykite mokiniams sistemingo darbo vaidmenį gilinant ir stiprinant žinias, apie užduočių atlikimo kultūrą;
Mokinių kūrybinių gebėjimų ugdymas.
Praktinių darbų atlikimas:
Praktinio darbo metodinių rekomendacijų teorinė medžiaga.
Matematika, – Serija: Vidurinis profesinis išsilavinimas. - Rostovas prie Dono „Feniksas“, p.
Praktinės pamokos eiga.
1.Pamokos temos formulavimas, temos sąsajos su kitomis akademinės disciplinos temomis paaiškinimas;
2.Mokinių pasirengimo pamokai tikrinimas;
3. Pamokos vedimas pagal temą ir pagal disciplinos darbo programą:
Studijuoti teorinę medžiagą tema „Funkcijų ribų skaičiavimas“.
Apsvarstykite tipinių užduočių sprendimo pavyzdžius.
Atlikite savarankišką funkcijų ribų skaičiavimo darbą, naudodami pirmą ir antrą reikšmingas ribas.
Atsakykite į saugumo klausimus.
Teorinė informacija ir metodinės rekomendacijos
apie problemų sprendimą.
1. Teorinės medžiagos pristatymas.
Norėdami apskaičiuoti funkcijos ribą taške, turite:
1) Vietoj kintamojo x pakeiskite tai, į ką x linksta.
2) Jei atlikę 1 veiksmą gausime neapibrėžtį https://pandia.ru/text/78/405/images/image003_6.png" width="19" height="22 src=">ir pakeiskite rodyklė su minusu: (x-a).
3) Jei atlikę 1 veiksmą gausime formos https://pandia.ru/text/78/405/images/image002_13.png" width="18" height="31 src="> neapibrėžtį susietas su trigonometrinių funkcijų reikšmėmis, turime naudoti pirmąją nepaprastą ribą.
Apibrėžimas. Pirmoji žymi riba vadinama riba
https://pandia.ru/text/78/405/images/image007_4.png" alt="$\displaystyle \lim_(x\to0)\dfrac(\sin x)(x)=1. $" width="102" height="52">!}
5) Apibrėžimas:Antroji nepaprasta riba vadinamas limitu

Šios ribos suteikiamas skaičius vaidina labai svarbų vaidmenį tiek matematinėje analizėje, tiek kitose matematikos šakose. Skambina numeriu natūraliųjų logaritmų bazė ( https://pandia.ru/text/78/405/images/image009_4.png" alt="$ e$" width="11" height="14">показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:!}
![]()
2. Studijuotos medžiagos konsolidavimas.
1 pavyzdys
https://pandia.ru/text/78/405/images/image015_1.png" width="28" height="30 src=">= -4
Naudojome taisyklę 1) ir vietoj x pakeitėme tai, ko x turėtų siekti, ty x=2.
2 pavyzdys
https://pandia.ru/text/78/405/images/image017_1.png" width="154" height="32 src=">.png" width="21" height="30 src=">= 5
3 pavyzdys
https://pandia.ru/text/78/405/images/image021_1.png" width="199" height="37 src=">.png" width="137" height="35 src=">. png" width="138" height="24 src=">=3+3=6
4 pavyzdys
https://pandia.ru/text/78/405/images/image004_7.png" width="22" height="31 src=">.png" width="104" height="46 src=">. png" height="30 src=">
5 pavyzdys
https://pandia.ru/text/78/405/images/image032_0.png" width="61" height="46 src=">.png" height="30 src=">=2
6 pavyzdys
https://pandia.ru/text/78/405/images/image036_0.png" width="18" height="28 src=">
b) 
V) 
3. Žinių, įgūdžių ir gebėjimų įtvirtinimas.
Atlikti savarankišką funkcijų ribų skaičiavimo darbą.
Praktinis darbas Nr.1. 1 variantas Apskaičiuokite funkcijos ribą: 1. 2. 3. 10. | Praktinis darbas Nr.1. 2 variantas Apskaičiuokite funkcijos ribą: 1. 2. 3. 10. |
Praktinis darbas Nr.2.
Tema : Funkcijos išvestinės radimas. Vieno kintamojo funkcijos tyrimas ir grafiko braižymas.
Tikslas : Praktiškai patikrinkite funkcijos išvestinės sampratos žinias, gebėjimą rasti elementariųjų funkcijų išvestines, kompleksines funkcijas, atvirkštines funkcijas, naudojant išvestinių lentelę ir diferenciacijos taisykles, kompleksinės ir atvirkštinės funkcijos sampratą, gebėjimą naudoti išvestinę funkcijoms tirti.
Praktinių darbų atlikimas:
Vadovėlis. "Matematika". – M.: Bustard, 2010 m.
Matematika. M: Forum-Infa 2008.
Individualios kortelės su praktinio darbo galimybe.
1. Funkcijos išvestinės teorinė medžiaga ir pavyzdžiai.
Apibrėžimas: Funkcijos f(x) (f"(x)) išvestinė taške x yra funkcijos padidėjimo ir argumento prieaugio santykio riba, kai argumento padidėjimas linkęs į nulį:
https://pandia.ru/text/78/405/images/image061_0.png" width="209 height=235" height="235">
Diferencijavimo taisyklės.
Jei funkcijos f(x) ir g(x) turi išvestines, tai
2. (u+v)′=u′+v′
3. (uv)′=u′v+v′u
4. (C u)′=C u′, kur C=const
5..png" width="49" height="54 src=">
6. Sudėtinės funkcijos išvestinė:
f′(g(x))=f′(g) g′(x)
2. Pavyzdžiai.
1..png" width="61" height="41 src=">.png" width="20" height="41 src=">.png" width="20" height="41 src="> .png" width="69" height="41 src=">+4).
Funkcija yra dviejų veiksnių sandauga: u=https://pandia.ru/text/78/405/images/image071_0.png" width="72" height="41 src=">.png" width=" 64" height="41 src=">.png" width="19" height="41 src=">.png" width="45" height="51 src=">.
Funkcija yra dviejų išraiškų koeficientas: u=https://pandia.ru/text/78/405/images/image079.png" width="52" height="41 src=">..png" width= "215" " height="57 src=">.png" width="197 height=36" height="36">
Sprendimas. Raskime šios funkcijos išvestinę naudodamiesi sudėtingų funkcijų diferenciacijos taisykle (6 formulė):

5. Jei , tada 
6. y = x 3 – 3x 2 + 5x+ 2. Raskime y "(–1).
y " = 3x 2 – 6x+ 5. Todėl y "(–1) = 14.
7. Jeigu y= žurnalas x cos x, Tai y" = (ln x)" cos x+ln x(cos x) " =1/x∙dėl x– ln x nuodėmė x.
Tegu duota funkcija. Norėdami jį studijuoti, jums reikia:
1) Raskite jo apibrėžimo sritį. Jei tai nėra per sunku, pravartu rasti ir diapazoną. (Tačiau daugeliu atvejų suradimo klausimas atidedamas, kol bus surastas funkcijos kraštutinumas.)
2) Išsiaiškinkite bendrąsias funkcijos savybes, kurios padės nustatyti jos elgesį: ar funkcija lyginė ar nelyginė, ar ji periodinė.
3) Išsiaiškinkite, kaip funkcija elgiasi argumentui priartėjus prie apibrėžimo srities ribinių taškų, jei tokių yra. Jei funkcija turi nenutrūkstamų taškų, šiuose taškuose taip pat reikia patikrinti, ar nėra funkcijos vertikalių asimptočių. Raskite pasvirusius asimptotus.
4) Raskite grafiko susikirtimo taškus su koordinačių ašimis, kuriuos sudaro tiesiog funkcijos reikšmės apskaičiavimas pagal sąlygą:
Su OX ašimi: y=0;
Su OY ašimi: x=0.
Radus susikirtimo su ašimi taškus, gali prireikti išspręsti sudėtingą algebrinę lygtį, kurią, ko gero, galima padaryti tik apytiksliai. Radę funkcijos šaknis ir nenutrūkstamumo taškus, galime nustatyti funkcijos ženklą kiekviename intervale tarp šių taškų. Tai galima padaryti apskaičiuojant funkcijos reikšmę bet kuriame intervalo taške arba naudojant intervalo metodą.
5) Raskite monotoniškumo intervalus. Norėdami tai padaryti, raskite išvestinę ir išspręskite nelygybę:
https://pandia.ru/text/78/405/images/image089.png" width="49" height="19 src=">, funkcija mažėja.
Radę monotoniškumo intervalus, iš karto galime nustatyti lokalaus ekstremumo taškus: kur padidėjimas pakeičiamas mažėjimu, yra lokalūs maksimumai, o kur mažėjimą pakeičia padidėjimas – lokalūs minimumai.
6) Išgaubtumo ir įgaubimo intervalai randami naudojant antrąją išvestinę..png" width="39" height="19 src="> intervaluose:
jei https://pandia.ru/text/78/405/images/image090.png" width="39" height="19 src=">‹0, tada funkcijos grafiko kreivė yra išgaubta.
Kartu mes apibrėžiame vingio taškus kaip tuos taškus, kuriuose funkcija keičia išgaubimo kryptį (ir yra tolydi).
7) Grafo susikirtimo su asimptote ir papildomais taškais taškų radimas. Šis taškas nėra privalomas, tačiau tokių taškų radimas leidžia atlikti funkcijos ir jos grafiko tyrimą.
Atkreipkite dėmesį, kad brėžinyje naudinga iš karto nubrėžti taškus koordinačių ašyse ir grafike, gautus tiriant funkcijas. Tai padeda suprasti grafiko išvaizdą kelyje.
3. Padarykite tai patys:
|
variantas | Raskite funkcijos y išvestinę: |
variantas | Raskite funkcijos y išvestinę: |
1.y=6- | 1. y=-6- 5.y= |
||
1. y=-7-1 | 1. y=-7-1 |
||
1.y=4x-3tgx+6x-8 | 1.y=-5x+2ctgx+3x-2 |
||
Pamokos tikslai:
Švietimo- žinoti diferenciacijos formules; diferenciacijos taisyklės;
sudėtingos funkcijos diferencijavimas; fizinė ir geometrinė išvestinės reikšmė;
funkcijos grafiko liestinės lygtis.
Vystomasis – mokėti rasti funkcijų išvestinius; spręsti uždavinius pasitelkiant fizinę reikšmę, geometrinę reikšmę; rasti funkcijos išvestinės reikšmę taške; matematiškai teisingai paaiškinti ir pagrįsti atliktus veiksmus.
Mokomasis – ugdyti savarankiškumą, atsakingumą, refleksiją.
Per užsiėmimus
I. Organizacinis momentas.
II. Namų darbų tikrinimas
(per pertraukas konsultantai tikrina (mokinius) ir skiria pažymius).
III. Tikslų nustatymas ir motyvacija
Mokytojas informuoja mokinius, kad ši pamoka yra baigiamoji pamoka tema „Išvestinių skaičiavimas“ ir kviečia juos suformuluoti savo tikslus.
Mokytojas: „Didysis filosofas Konfucijus kartą pasakė: „Trys keliai veda į pažinimą: apmąstymų kelias yra kilniausias kelias, mėgdžiojimo kelias yra lengviausias, o patirties kelias yra karčiausias. Taigi šiandien klasėje kiekvienas iš jūsų nuspręs, kuriuo keliu į pažinimą šia tema jis eina.
Mokiniams suteikiama užduotis pademonstruoti savo žinias ir įgūdžius skaičiuojant išvestines ir pateikiamas pamokos planas.
I etapas: Užduoties atlikimas naudojant kortelę „Prisiminti“.
(formulių ir diferenciacijos taisyklių žinių tikrinimas).
II etapas:Žodinis frontalinis darbas apie žinių kartojimą ir apibendrinimą.
III etapas:„Bandomoji prognozė“ (atliekant šią užduotį priimtina konsultantų pagalba).
ašV etapas: Praktinės problemos sprendimas.
V etapas: Savarankiškas darbas
Vertinami I, III, V darbo ir namų darbų etapai. Konsultantai patikrina ir įrašo rezultatus į vertinimo lentelę.
Vertinimo kriterijus: "5"- 19-20 taškų;
"4"- 15-18 taškų;
"3"- 10-14 taškų.
Keliai į pažinimą
- Pamatinių žinių atgaminimas ir taisymas
I etapas.
Tikslas: formulių ir diferenciacijos taisyklių žinojimo kontrolė, savikontrolė
Prisiminti! F.I. _______________________________________________________ |
|
Darinys |
|
c,c - minusai t |
|
|
|
|
|
f"(x)+ g"(x) |
|
f(x)* g(x) |
|
|
|
Šios užduoties pabaigoje atliekamas savęs patikrinimas naudojant „Išvestinių priemonių lentelę“. Kortelės perduodamos patikrinti konsultantams (kortelių taisymai neleidžiami).
V. Žinių apibendrinimas ir sisteminimas
II etapas.
1. Žodinis frontalinis darbas.
A. Sukurkite šios sąlygos užduotį ir ją išspręskite.
![]()
1. Raskite funkcijos išvestinės reikšmę taške t = 3. (Atsakymas: 21.)
2. Sukurkite funkcijos grafiko liestinės taške t = 3 lygtį. (Atsakymas: y = 21x-45.).
3. Raskite kūno greitį ir pagreitį momentu t=3c, jei judėjimo dėsnis pateiktas formule. (Atsakymas: 21 m/s, 16 m/s²).
4. Raskite funkcijos grafiko liestinės kampinį koeficientą, nubrėžtą taške t = 3. (Atsakymas: 21.).
5. Raskite funkcijos grafiko liestinės polinkio kampo liestinę taške t = 3 ir nustatykite kampo tarp liestinės ir teigiamos Ox ašies krypties tipą. (Atsakymas: tgα, kampas α yra smailus)
B. Raskite funkcijų išvestines

2. III etapas„Bandomoji prognozė“


Šios užduoties pabaigoje pagal galutinius atsakymus atliekamas savęs patikrinimas ir testai perduodami konsultantams. (kortelių taisymai neleidžiami).
Atsakymai:
1 variantas |
||||
2 variantas |
- Problemos sprendimas
ašV etapas
Frontalinis pažengusio lygio problemos sprendimas (sprendimą atlieka konsultantai kartu su klase).
Užduotis
Kokiomis parametrų reikšmėmis a funkcijos grafiko liestinės ![]()
nubrėžtos jos susikirtimo su X ašimi taškuose, sudaryti tarpusavyje 60° kampą?

Grafikas yra parabolė su aukštyn esančiomis šakomis, kertančiomis X ašį dviejuose taškuose (atvejis a=0 neatitinka problemos prasmės):
IX. Apibendrinimas ir įvertinimas
1. Klausimai: a) Ar buvo pasiektas pamokos tikslas?
b) Kuris etapas atrodė sunkiausias?
c) Kas buvo įdomiausia?
2. Konsultantai paskelbia rezultatus (mokinių skaičius ir pavardės pakeliui).
imitacija, refleksijos būdai ir patirties būdai).
Praktinė pamoka
Tema: Darinių paieška. Išvestinės taikymas funkcijų tyrimui ir grafikų braižymui.
Tikslas: Įvaldykite išvestinių skaičiavimų, išmokite tyrinėti funkciją naudojant išvestinę
Mokymosi priemonės: sąsiuviniai praktiniams pratimams, pristatymai ta tema, interneto šaltiniai.
1. Apsvarstykite teorinę medžiagą temomis: „Išvestinių skaičiavimo taisyklės“, „Funkcijos ekstremumas“, „Išgaubtumas, įgaubimas. Vingio taškas."
2. Peržiūrėkite užduočių pavyzdžius.
3. Atlikite testo užduotį Nr.
Kontroliniai klausimai:
1. Apibrėžkite funkcijos maksimumą (minimumą) taške. Ką galima pasakyti apie funkcijos prieaugio ženklą gana mažoje didžiausio (minimalaus) taško kaimynystėje?
2. Kokios būtinos sąlygos egzistuoti funkcijos ekstremumui? Kokia jų geometrinė reikšmė?
3. Kokia yra taisyklė, leidžianti rasti didžiausią ir mažiausią funkcijos reikšmes segmente?
4. Apibrėžkite intervalo kreivės išgaubimą (įgaubą).
5. Kokia yra kreivės išgaubimo ir įgaubimo intervalų nustatymo taisyklė?
6. Kreivės vingio taškas. Kaip ją rasti?
7. Koks yra funkcijos grafiko sudarymo algoritmas?
Išvestinių finansinių priemonių skaičiavimo taisyklės
Sudėtingos funkcijos išvestinė.
Jeigu adresu=ƒ( Ir), u=φ(x), tada adresu¢ ( X)=ƒ¢ (i)·φ¢ (X).
Sumos išvestinė.
Jeigu adresu(X)=Ir(X)+v (X), tai adresu¢ (X)=Ir¢ (X)+v ¢ (X)
Produkto darinys.
Jeigu y(x)=u(X)· v (X), tai adresu¢ = Ir¢ · v + u · v ¢ .
Visų pirma, ( Su· Ir)¢ =c· Ir¢, ty pastovus koeficientas išimamas iš po išvestinio ženklo. Tai lengva patikrinti
(u 2 ) ¢ = 2 u·u ¢ , (u 3 ) ¢ =3u 2 u ¢ , … , (u n ) ¢ =n·u n–1 u ¢ .
Dalinio išvestinė.
Jei tada  .
.
Išvestinių priemonių lentelė
1. (Su)¢ =0
Sudėtingai funkcijai: jei u=u(x), Tai:
2. (X)¢ =1
3. (X α )¢ = α · Xα–1, A– bet koks tikrasis skaičius.
 .
.
3. 

4. (A X ) ¢ =a X · ln A
4. 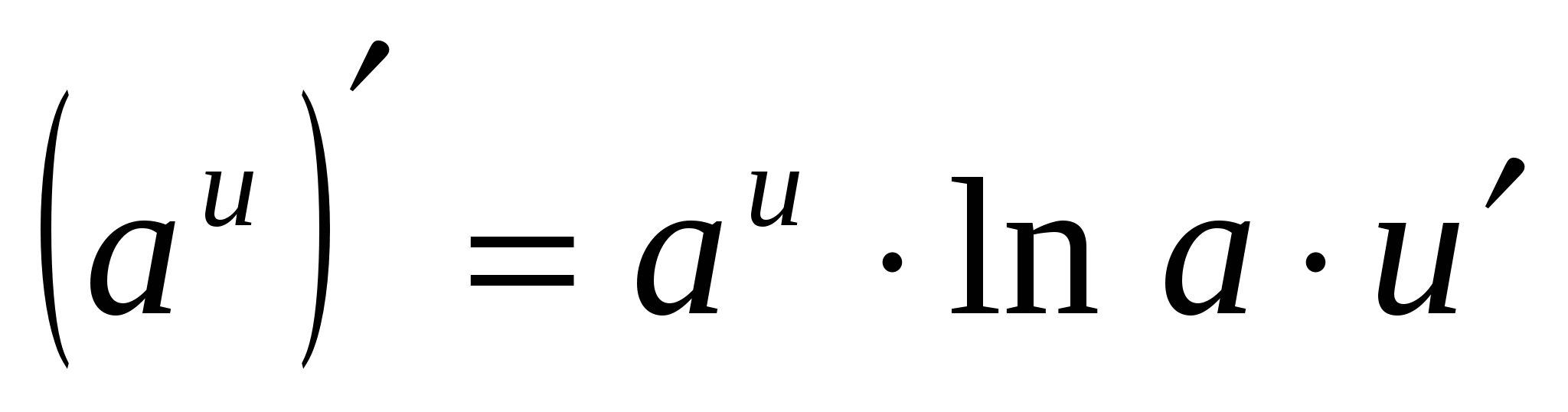

5. (žurnalas
a
x)
¢
=
 .
.
5. 

6. (nuodėmė x)¢ = cos x
6. 
7. (cos x)¢ = –sin x
7. 
8. (tg x)¢
=
8. 
9. (ctg x)¢
=
9. 
10. 
10. 
11. 
11. 
12. 
12. 
13. 
13. 
Peržiūrėkite pavyzdžius
1 pavyzdys.
y=(3–2 sin 5x ) 4 | Taikome išvestines formules Ir α , nuodėmė u |
y ¢ =4·(3–2·sin5x) 3·(3–2sin5x) ¢ =4·(3–2·sin5x) 3 ·(0–2·cos5x·5) = –40·(3–2·sin5x) 3 .
2 pavyzdys.
. 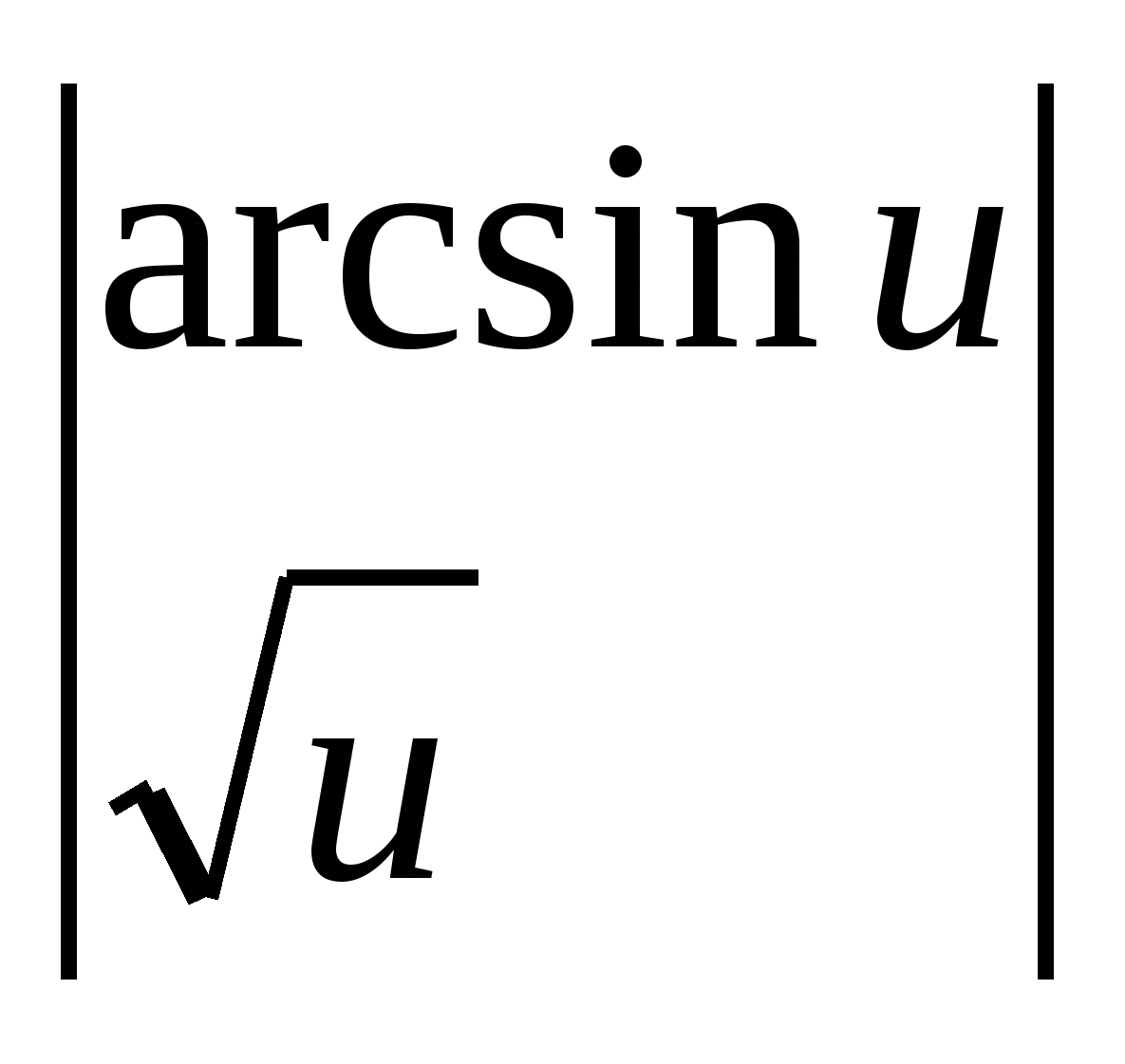

3 pavyzdys.
 .
. 

4 pavyzdys.



5 pavyzdys.
 .
. 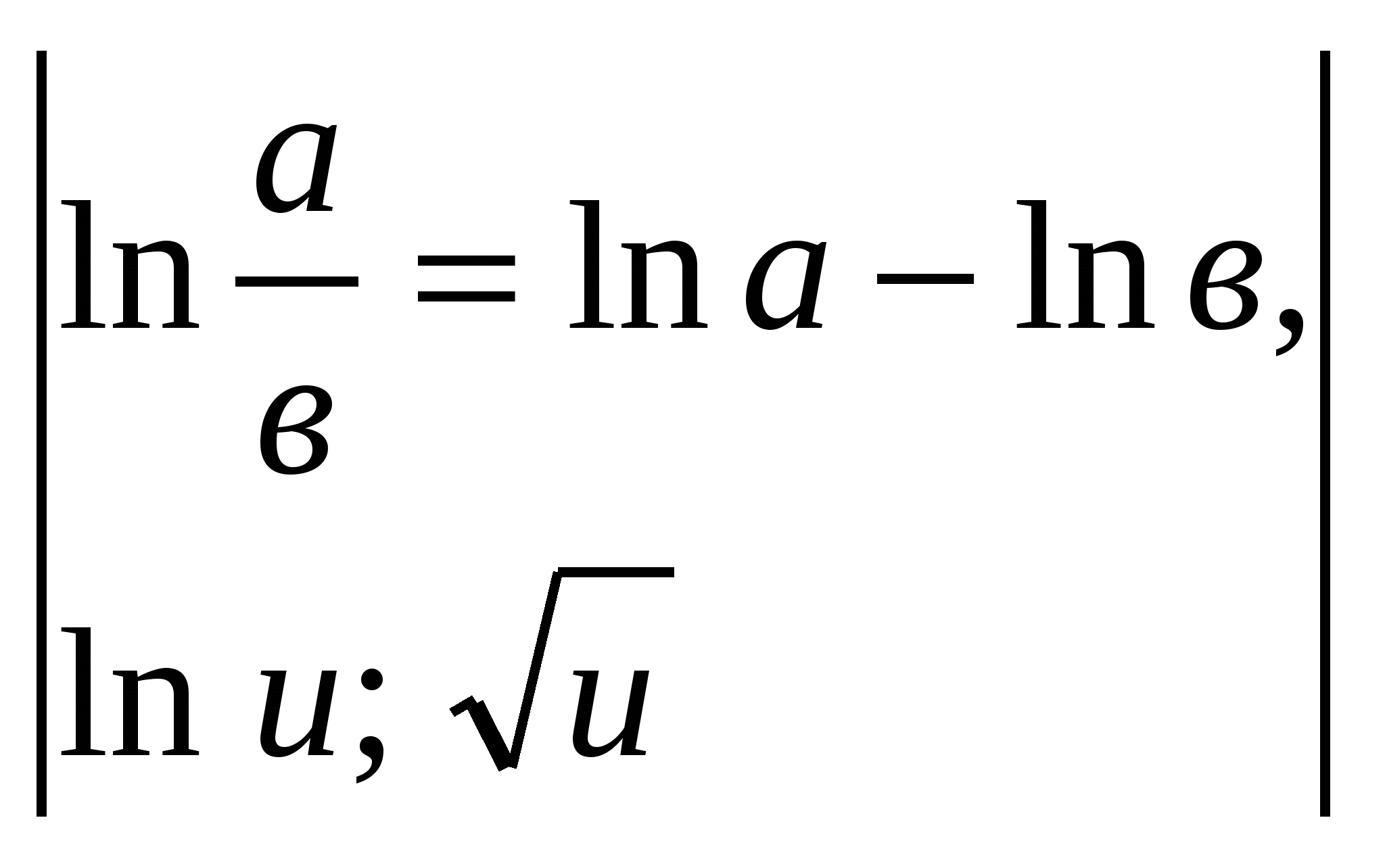

Funkcijos ekstremumas
Funkcijos ties ekstremumu tyrimas yra vienas iš svarbiausių išvestinių pritaikymų. Pažvelkime į minimumų ir maksimumų apibrėžimus ir kaip juos rasti.
Tegul funkcija ƒ( X) yra apibrėžtas ir diferencijuojamas tam tikroje aibėje ir taške X 0 yra taškas jo viduje.
Apibrėžimas. Funkcija ƒ (X) taške X 0 turi maksimalus(mažiausiai), jei yra tokia taško kaimynystė X 0, kuris tinka visiems X iš šios srities ƒ (X) < ƒ (X 0 ) (ƒ (X) > ƒ (X 0 )).
Taškas X 0 tada vadinamas tašku maksimalus(minimumas).

Ryžiai. 1.
Rodomas funkcijos, turinčios du maksimalius taškus ( X 1 ir X 3) ir du minimalūs taškai ( X 2 ir X 4), o didžiausia vertė gali būti mažesnė už mažiausią ( ƒ (X 1 ) < ƒ (X 4)). Tai pabrėžia faktą, kad funkcijos singuliarumą apibūdiname tik netoli tam tikro taško.
Funkcijos reikšmės didžiausio ir minimumo taškuose vadinamos ekstremaliomis reikšmėmis arba kraštutinumai. Aukščiau pateikta diagrama rodo, kad kraštutiniai taškai ( X 1 , X 2 , X 3 , X 4) nustatyti funkcijos monotoniškumo intervalus, kurių kiekviename išvestinė išlaiko tam tikrą ženklą. Ekstremaliuose taškuose, žinoma, išvestinė eina į nulį. Suformuluokime teoremą apie būtina sąlyga ekstremumo buvimas.
Teorema. Jei funkcija ƒ (X) taške X 0 turi ekstremumą, tada funkcijos išvestinė šiame taške yra lygi nuliui, ty ƒ¢ ( X 0)=0.
Iš karto pastebėkime, kad šios sąlygos nepakanka, t. y. atvirkštinis teiginys ne visada teisingas. Iš lygybės ƒ ¢ ( X 0)= 0 nebūtinai reiškia, kad taške X 0 yra ekstremumas.
Tai patvirtina pavyzdys su funkcija ƒ (X)=x 3 .
Mes surasime ƒ ¢ ( X)= 3X 2 . Taške X=0 ƒ ¢ (0) = 0 . Bet taip arti taško, kiek norite X=0 rasime X> 0, kur ƒ (X)=x 3 > 0, rasime X< 0, где ¦ (X)=X 3 < 0. Т. е. не существует какая-либо малая окрестность точки X=0, kur visiems X funkcijos reikšmė taške X=0 bus didžiausias arba mažiausias. Todėl taškas X=0 nėra ekstremumo taškas.
Galima ginčytis kitaip. Kadangi vedinys ƒ ¢ (x) = 3x 2 , tada funkcija ƒ(x)=x 3 didėja bet kuriam realiam x ir neturi ekstremalių.
Taškai, kuriuose įvykdoma būtinoji ekstremalioji sąlyga (ƒ ¢ (x) = 0) yra vadinami kritiškas .
Akivaizdu, kad funkcijos grafiko liestinė taškuose, kur ƒ ¢ (x) = 0, lygiagrečiai x ašiai Ox .
Pakankama būklė ekstremumas pateiktas šiose teoremose.
1 teorema. Jeigu X 0 yra funkcijos kritinis taškas ir per jį pereinant išvestinė keičia ženklą, tada X 0 yra ekstremumo taškas, būtent, jei išvestinė keičia ženklą iš pliuso į minusą, tai yra maksimalus taškas, o jei keičia ženklą iš minuso į pliusą, tai yra minimalus taškas.
Atkreipkite dėmesį, kad taške nėra ekstremumo, jei išvestinė nekeičia ženklo. Ekstremo tyrimo taisyklė naudojant pirmąjį vedinį yra žinoma iš mokyklos kurso. Kartais patogiau suformuluoti pakankamą ekstremumo sąlygą naudojant antrąjį darinį.
Tegul funkcija ƒ( X) yra du kartus diferencijuojamas kai kuriose srityse (t. y. ƒ( X) turi ƒ¢ ( X) Ir ƒ ¢¢ ( X)).
2 teorema. Jeigu X 0 – kritinis funkcijos taškas ƒ(x) ir ƒ ¢¢ (X 0 ) > 0 , Tai X 0 – minimalus balas, jei ƒ ¢¢ (X 0 ) < 0, то X 0 – maksimalus taškas.
Naudojant antrąją išvestinę, nustatomas funkcijos grafiko išgaubimas arba įgaubimas.
Išgaubtumas, įdubimas. Vingio taškas.
Kreivė y=ƒ(X) vadinamas išgaubtasth žemiau bet kuri iš jos liestinė
ƒ ¢¢ ( X) < 0.
Kreivė y=ƒ(X) vadinamas įgaubtas intervale, jei visi kreivės taškai yra aukštesnė bet kuri iš jos liestinė šiuo intervalu. Tada per šį intervalą
ƒ ¢¢(x) > 0
Apibrėžimas. Vingio taškas kreivė yra taškas, kuriame kreivė yra išgaubta vienoje pusėje, o kita - įgaubta.
Posūkio taške ƒ ¢¢ ( X)=0.
Taigi antrosios išvestinės (taip pat ir pačios funkcijos bei pirmosios jos išvestinės) ženklas nurodo funkcijos grafiko požymius. Pažvelkime į juos dar kartą.
Jei visiems X per intervalą ( A, b) ƒ (X) > 0 (ƒ (X) < 0), tada grafikas yra virš (žemiau) x ašies.
Jei visiems X per intervalą ( A, b) ƒ ¢ ( X) > 0 (ƒ ¢ ( X) < 0), то функция на (A, b) didėja (mažėja).
Jei visiems X per intervalą ( A, b) ƒ ¢¢ ( X) > 0 (ƒ ¢¢ ( X) < 0), то график на (A, b) įgaubtas (išgaubtas).
Lygtis ƒ( X)=0 apibrėžia funkcijos „nulius“, t. y. grafiko susikirtimo taškus su Ox ašimi.
Lygtis ƒ ¢ ( X)=0 apibrėžia kritinius taškus.
Lygtis ƒ ¢¢ ( X)=0 apibrėžia galimus vingio taškus.
Funkcijų tyrimo schema
Norėdami ištirti funkciją ƒ (X) ir planavimas y=ƒ(X) reikia rasti:
1) funkcijos apibrėžimo sritis ir grafiko susikirtimo taškas su koordinačių ašimis;
2) monotonijos intervalai;
3) ekstremalių taškai ir funkcijų reikšmės šiuose taškuose;
4) grafiko išgaubtumo ir įgaubtumo intervalai;
5) grafiko vingio taškai;
6) Dekarto koordinačių sistemoje sukonstruoti visus gautus taškus (kartais, norint patikslinti grafiką, gaunami papildomi taškai) ir patį grafiką.
Mažiausia ir didžiausia segmento funkcijos reikšmės
Sprendžiant kai kurias optimizavimo metodo problemas, svarbu, kad tam tikrame segmente būtų galima rasti mažiausias arba didžiausias funkcijos reikšmes. Funkcija pasiekia šias reikšmes arba kritiniuose taškuose, arba segmento galuose.
Paieškos schema mažiausios ir didžiausios funkcijos reikšmės ƒ (X) segmente [ A, b].
1. Raskite funkcijos išvestinę ƒ ¢ ( X).
2. Raskite lygties kritinius taškus ƒ ¢ ( X)=0.
3. Pasirinkite tuos kritinius taškus, kurie priklauso šiam segmentui [ A, b] ir raskite funkcijos reikšmę ƒ (X) kiekviename tokiame taške.
4. Apskaičiuokite funkcijų reikšmes ƒ (X) segmento galuose: ƒ( A) ir ƒ( b).
5. Iš gautų funkcijų reikšmių pasirinkite didžiausią (didžiausią) ir mažiausią (mažiausią).
2 pavyzdys.
Raskite didžiausią ir mažiausią funkcijos reikšmes ƒ(x)=X 3 – 9x 2 +24х–10 segmente.
1. ƒ ¢ ( X)= 3X 2 – 9 · 2 X 2 + 24.
2. ƒ ¢ ( X)=0, 3(X 2 –6X+8)=0, X 1 =2, X 2 =4.
3. Taškas x 2 =4 atkarpai nepriklauso. Todėl funkcijos reikšmę skaičiuojame tik taške X 1 =2
ƒ(2)=2 3 –9·2 2 +24·2–10=10.
4. Funkcijų reikšmės atkarpos galuose: ƒ(0)= –10, ƒ(3)=3 3 –9·3 2 +24·3–10, ƒ(3)=8.
5. Gautos vertės:
ƒ(2)=10, ƒ(0)= –10, ƒ(3)=8.
Didžiausia vertė yra 10 ir pasiekiama taške X=2. Mažiausias lygus –10 ir pasiekiamas taške X=0.
3 pavyzdys.
Raskite kreivės išgaubimo ir įgaubimo intervalus bei vingio taškus y=x+36X 2 –2X 3 –X 4 .
Šios funkcijos apibrėžimo sritis yra visų realiųjų skaičių aibė, t.y. XЄ(–∞, +∞).
Raskime antrąją išvestinę.
adresu¢ = 1+72 X–6X 2 –4X 3 .
adresu¢¢ =72–12 X–12X 2 = –12(X 2 +X–6).
Iš Eq. adresu¢¢ =0 gauname vingio taško abscisę:
–12(X 2 +X–6)=0 X 1 = –3; X 2 =2.
Apibrėžkime ženklą adresu¢¢ intervalais
(–∞; –3), (–3; 2), (2, +∞).
X
(–∞, –3)
(–3; 2)
(2; +∞)
adresu¢¢
kreivės forma
išgaubtas
linksniavimas
įgaubtas
linksniavimas
išgaubtas
Raskime vingio taškų ordinates:
adresu(–3)=726; M 1 (–3; 726) – vingio taškas
adresu(2)=114; M 2 (2; 114) – vingio taškas.
Intervale (–3; 2) kreivė yra įgaubta. Ant intervalų (–∞; –3) ir (2; +∞) – išgaubtas.
Užduočių pavyzdžiai
Užduotis Nr.1.
Raskite funkcijos lūžio taškus ir nubraižykite grafiką

Funkcija ƒ (X) yra apibrėžtas visiems realiems X ir yra tęstinis kiekviename iš nurodytų intervalų: (–∞; –1), [–1; 0], (0, +∞). Panagrinėkime funkciją ƒ (X) tęstinumui taškuose X= –1 ir X=0.
Norėdami tai padaryti, kiekviename iš šių taškų rasime vienpuses ribas.

Kadangi vienpusės ribos yra skirtingos, tada X = –1 – pirmosios rūšies nepertraukiamumo taškas.

Vienpusės ribos yra lygios, t.y. taške x=0 yra funkcijos ir 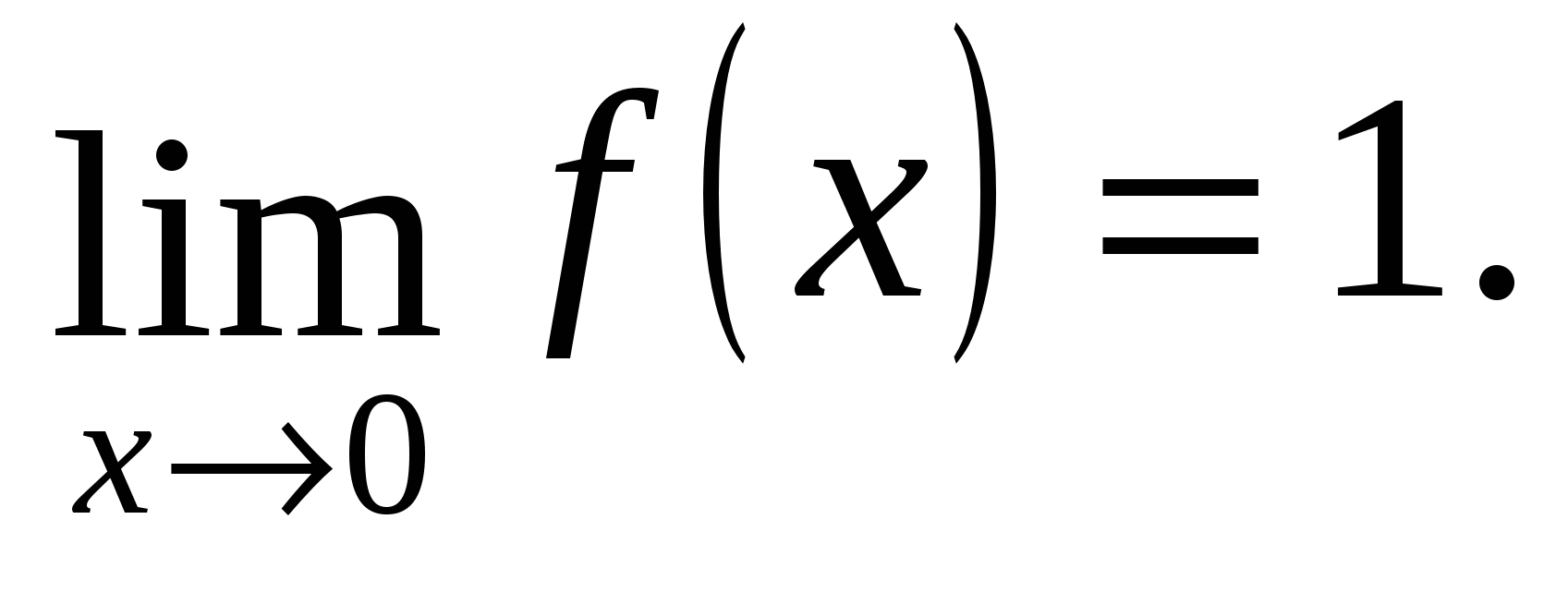
Palyginkime šią ribą su funkcijos reikšme taške: 
Nes  tada į esant x=0 funkcija ƒ(x) yra tolydi.
tada į esant x=0 funkcija ƒ(x) yra tolydi.
Nubraižykime funkciją ƒ (X), turint omenyje
1)  – tiesės lygtis,
– tiesės lygtis,
2)  – viršutinio puslankio lygtis
– viršutinio puslankio lygtis  kurio centras ištakoje ir spindulys lygus vienetui, o su sąlyga –1 £ X 0 svarų lygtis
kurio centras ištakoje ir spindulys lygus vienetui, o su sąlyga –1 £ X 0 svarų lygtis  apibrėžia ketvirčio apskritimą.
apibrėžia ketvirčio apskritimą.
3) už X > 0 grafikas pateikiamas lygtimi  . Iš lygties randame šios kreivės susikirtimo taškus su Ox ašimi
. Iš lygties randame šios kreivės susikirtimo taškus su Ox ašimi  jei x > 0. x= π
n, Kur n
=1, 2, 3, 4,
jei x > 0. x= π
n, Kur n
=1, 2, 3, 4,

Ryžiai. 2.
2 užduotis.
Parašykite tiesės liestinių lygtis  taškuose, kur X=0 ir X=4. Raskite liestinių susikirtimo tašką ir kampą tarp jų. Padarykite piešinį.
taškuose, kur X=0 ir X=4. Raskite liestinių susikirtimo tašką ir kampą tarp jų. Padarykite piešinį.
Tiesės liestinės lygtis y=ƒ(x) atrodo kaip
Kur adresu 0 =ƒ( X 0).
Taške X=0 adresu(0)=ƒ(0)=5.
adresu¢ =ƒ ¢ (X)=X–3 ƒ¢ (0)= –3.
M 1 (0, 5) turi formą y- 5= –3(X–0) arba
y= –3X+5.
Taške X=4 adresu(4)=ƒ(4)=1. ƒ¢ (4)=4–3=1.
Liestinės taške lygtis M 2 (4, 1) turi formą y- 1=X– 4 arba
y=x–3.
Išspręsdami sistemą gauname liestinių susikirtimo tašką

Susikirtimo taškas M 3 (2, –1).
Kampas φ tarp liestinių randame iš formulės:
 ,
,
Kur k 1 = –3; k 2 =1 – liestinių kampiniai koeficientai.
 .
.
Kampas φ =arctg 2.
Pastatykime šią liniją  – parabolė su viršūne taške, kur X=3, nes adresu¢
=0 at X=3. Mes surasime
– parabolė su viršūne taške, kur X=3, nes adresu¢
=0 at X=3. Mes surasime  . Taškas M 4 (3;
. Taškas M 4 (3;  ) yra parabolės viršūnė.
) yra parabolės viršūnė.
R 
yra. 3.
Užduotis Nr.3.
Naršyti funkciją  ir suplanuoti.
ir suplanuoti.
1. Ši funkcija yra daugianario (galite atidaryti skliaustus, gauname trečiojo laipsnio daugianarį), todėl ji yra apibrėžta, tęstinė ir diferencijuojama bet kokiai X.
2. Raskime išvestinę.
 .
.
Iš Eq. adresu¢ =0 Raskime kritinius taškus: 3 X·( X–2)=0, X 1 =0, X 2 =2.
Patyrinėkime juos.
X
(–∞, 0)
(0; 2)
(2; +∞)
adresu ¢
adresu
3. Taigi, funkcija didėja intervalais (–∞, 0) ir (2, +∞), mažėja intervale (0; 2), turi maksimumą ties x=0 ir minimumą, kai x=2:
adresu max = adresu(0)=4; adresu min = adresu(2)=0.
4. Raskime antrąją išvestinę.
adresu¢¢ = 6·( X-1).
Kreivė yra išgaubta kur adresu¢¢ < 0, т. е. 6·(X–1) < 0, X < 1.
Kreivė įgaubta kur adresu¢¢ > 0, t.y. X > 1.
Taigi intervale (–∞, 1) kreivė yra išgaubta; o intervale (1, +∞) jis yra įgaubtas.
5. Iš lygties randame vingio tašką adresu¢¢ =0. Taigi, X=1 – vingio taško abscisė, nes šis taškas atskiria kreivės išgaubimo ir įgaubimo intervalus. Posūkio taško ordinatė: adresu(1)=2.
Funkcijos grafikas adresu=(X+1)·( X–2) 2 kerta Ox ašį ties adresu=0, t.y. kada X= –1 ir X=2;
kerta Oy ašį ties X=0, t.y. kada adresu=4. Gavome tris taškus: (–1; 0), (2; 0), (0; 4). Visus gautus taškus surašysime į lentelę, pridėdami prie jų esančius.
–2
–1



–16


yra. 4 Kreivė y=(x+1)(x–2) 2.
Užduotis Nr.1
Pateikiame jums užduotis, kuriose gali būti vienas, du, trys ar daugiau teisingų atsakymų. Apibraukite visų teisingų atsakymų skaičius.
1. Jeigu  tada funkcija
tada funkcija
1) didėja
2) mažėja
3) pastovus
2. Jeigu
1) Didėja
2) Mažėja
3. Jeigu  , tada funkcija
, tada funkcija
1) Didėja
2) Mažėja
4. Jei  , tada funkcija
, tada funkcija
1) Didėja 3) Mažėja
2) Pastovi 4) Monotoniška
5. Funkcija  Is
Is
1) net
2) Netgi ne
3) nei lyginis, nei nelyginis
4) Periodinis
5) Ne periodiškai
6) Trigonometrinis
7) Elementarus
6. Funkcija  Is
Is
1) net
2) nelyginis
3) nei lyginis, nei nelyginis
4) periodinis
5) ne periodinis
6) trigonometrinis
7) elementarus
2) Weierstrassas 4) Dirichlet 6) Leibnicas
8) Sprendimas  Lygtys
Lygtys
1) 0 3) 0 ir 3 5) 2 7) 3
2) 2 ir 3 4) 2 6) -5 ir 1 8) 5 ir 1
9) nelygybės sprendimas 
1) ( ; 1) 3) (
; 1) 3) ( ; 1) 5) (-
; 1) 5) (- ;1)
;1)
2) (1; 5) 4) (2;  ) 6)
) 6) 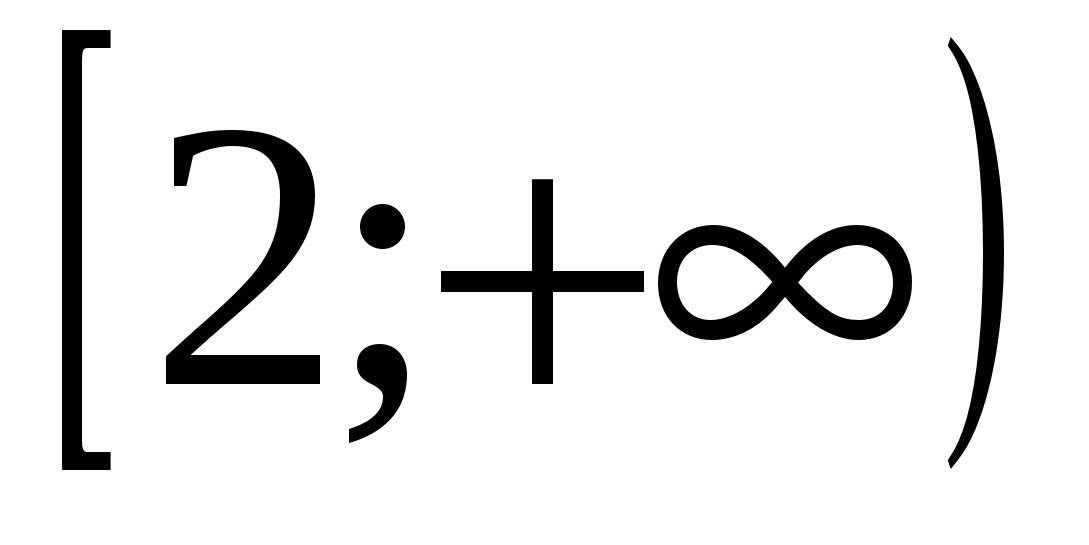
10) Metodas  Suma rasta
Suma rasta
1) vektoriai
2) tiesus
3) segmentas
11) Jei  , tada funkcija
, tada funkcija
1) Įgaubtas 3) Išgaubtas 5) Mažėjantis
2) Monotoniškas 4) Didėjantis 6) Pastovus
12) funkcijos apibrėžimo sritis lygi 
1) ( ;0)
;0)
2) (0;  )
)
3) (- ;
; )
)
4) (0;1)
5) 
6) 
7) (-1;1)
8) 
9) 
13) funkcija  yra
yra
1) orientacinis
2) trigonometrinis
3) galia
4) logaritminis
14) jei funkcijos y = x  tada ji yra
tada ji yra 
1) net
2) nelyginis
3) nei lyginis, nei nelyginis
15) funkcija  adresu
adresu  yra
yra

 .
.



