Statmenumas erdvėje gali turėti:

1. Dvi tiesios linijos

3. Du lėktuvai

Pažvelkime į šiuos tris atvejus paeiliui: visus su jais susijusių teoremų apibrėžimus ir teiginius. Ir tada aptarsime labai svarbią teoremą apie tris statmenus.

Dviejų linijų statmenumas.

Apibrėžimas:

Galima sakyti: Ameriką jie atrado ir man! Tačiau atminkite, kad erdvėje viskas nėra taip, kaip lėktuve.

Plokštumoje tik šios (susikertančios) linijos gali būti statmenos:

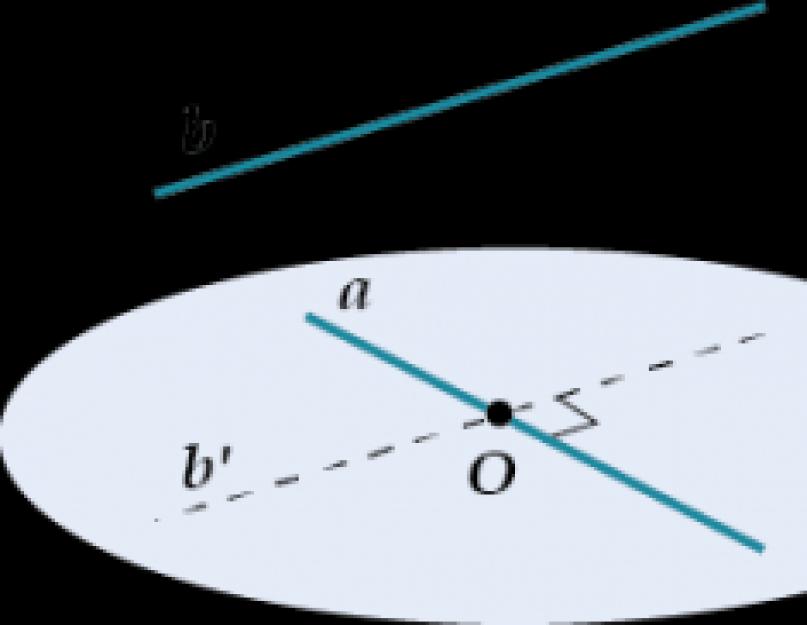
Tačiau dvi tiesios linijos gali būti statmenos erdvėje, net jei jos nesikerta. Žiūrėk:

tiesė yra statmena tiesei, nors su ja nesikerta. Kaip tai? Prisiminkime kampo tarp tiesių apibrėžimą: norėdami rasti kampą tarp susikertančių linijų ir, turite nubrėžti tiesią liniją per savavališką tašką tiesėje a. Ir tada kampas tarp ir (pagal apibrėžimą!) bus lygus kampui tarp ir.

Ar prisimeni? Na, mūsų atveju, jei tiesios linijos ir pasirodo esančios statmenos, tuomet turime atsižvelgti į tiesias linijas ir būti statmenomis.

Dėl visiško aiškumo pažiūrėkime pavyzdys. Tegul būna kubas. Ir jūsų prašoma rasti kampą tarp linijų ir. Šios linijos nesikerta – jos susikerta. Norėdami rasti kampą tarp ir, nubrėžkime.

Dėl to, kad tai lygiagretainis (ir net stačiakampis!), paaiškėja, kad. O dėl to, kad tai kvadratas, taip ir išeina. Na, tai reiškia.

Tiesės ir plokštumos statmena.

Apibrėžimas:

Štai paveikslėlis:

tiesė yra statmena plokštumai, jei ji statmena visoms, visoms tiesioms šios plokštumos: ir, ir, ir, ir net! Ir dar milijardas tiesioginių!

Taip, bet kaip tada apskritai galima patikrinti statmenumą tiesėje ir plokštumoje? Taigi gyvenimo neužtenka! Bet mūsų laimei, matematikai mus išgelbėjo nuo begalybės košmaro išradę tiesės ir plokštumos statmenumo ženklas.

Mes formuluojame:

Įvertinkite, koks jis puikus:

jei plokštumoje, kuriai tiesė yra statmena, yra tik dvi tiesės (ir), tada ši tiesė iš karto pasirodys statmena plokštumai, tai yra visoms tiesioms šioje plokštumoje (įskaitant kai kurias tieses šone stovinčią liniją). Tai labai svarbi teorema, todėl jos reikšmę nubraižysime ir diagramos pavidalu.

Ir pažiūrėkime dar kartą pavyzdys.

Leiskite mums pateikti taisyklingą tetraedrą.

Užduotis: įrodyk. Sakysite: tai dvi tiesios linijos! Ką su tuo turi tiesės ir plokštumos statmena?!

Bet žiūrėk:

pažymėkime krašto vidurį ir nubrėžkime ir. Tai yra medianos ir. Trikampiai yra taisyklingi ir...

Štai, stebuklas: pasirodo, kad nuo ir. Ir toliau, iki visų tiesių plokštumoje, o tai reiškia ir. Jie tai įrodė. O svarbiausias dalykas buvo būtent tiesės ir plokštumos statmenumo ženklo naudojimas.

Kai plokštumos statmenos

Apibrėžimas:

Tai yra (daugiau informacijos žr. temoje „dvikampis kampas“) dvi plokštumos (ir) yra statmenos, jei paaiškėja, kad kampas tarp dviejų statmenų (ir) į šių plokštumų susikirtimo liniją yra lygus. Ir yra teorema, kuri jungia statmenų plokštumų sąvoką su statmenumo sąvoka tiesės ir plokštumos erdvėje.

Ši teorema vadinama

Plokštumų statmenumo kriterijus.

Suformuluokime:

Kaip visada, žodžių „tada ir tik tada“ dekodavimas atrodo taip:

• Jei, tada eina per statmeną į.

• Jei jis eina per statmeną į, tada.

(natūralu, čia mes lėktuvai).

Ši teorema yra viena svarbiausių stereometrijoje, bet, deja, ir viena sunkiausiai pritaikomų.

Taigi jūs turite būti labai atsargūs!

Taigi, formuluotė:

Ir vėl iššifruoti žodžius „tada ir tik tada“. Teorema vienu metu teigia du dalykus (žiūrėkite paveikslėlį):

pabandykime pritaikyti šią teoremą uždaviniui išspręsti.

Užduotis: pateikta taisyklinga šešiakampė piramidė. Raskite kampą tarp linijų ir.

Sprendimas:

Dėl to, kad taisyklingoje piramidėje viršūnė, projektuojant, patenka į pagrindo centrą, išeina, kad tiesė yra tiesės projekcija.

Bet mes žinome, kad jis yra taisyklingame šešiakampyje. Taikome trijų statmenų teoremą:

Ir rašome atsakymą: .

TIESIŲ STAPETUMAS ERDVĖJE. TRUMPAI APIE PAGRINDINIUS DALYKUS

Dviejų linijų statmenumas.

Dvi linijos erdvėje yra statmenos, jei tarp jų yra kampas.

Tiesės ir plokštumos statmena.

Tiesė yra statmena plokštumai, jei ji yra statmena visoms tos plokštumos tiesėms.

Plokštumų statmenumas.

Plokštumos yra statmenos, jei dvikampis kampas tarp jų yra lygus.

Plokštumų statmenumo kriterijus.

Dvi plokštumos yra statmenos tada ir tik tada, kai viena iš jų eina per statmeną kitai plokštumai.

Trijų statmenų teorema:

Na, tema baigta. Jei skaitote šias eilutes, tai reiškia, kad esate labai šaunus.

Nes tik 5% žmonių sugeba ką nors įvaldyti patys. Ir jei perskaitėte iki galo, tada esate šiame 5%!

Dabar svarbiausia.

Jūs supratote šios temos teoriją. Ir, kartoju, tai... tai tiesiog super! Jūs jau esate geresnis už didžiąją daugumą jūsų bendraamžių.

Problema ta, kad to gali nepakakti...

Kam?

Už sėkmingai išlaikiusį vieningą valstybinį egzaminą, už įstojimą į kolegiją neviršijant biudžeto ir, SVARBIAUSIA, visam gyvenimui.

Niekuo neįtikinsiu, pasakysiu tik vieną dalyką...

Žmonės, gavę gerą išsilavinimą, uždirba daug daugiau nei tie, kurie jo negavo. Tai yra statistika.

Tačiau tai nėra pagrindinis dalykas.

Svarbiausia, kad jie būtų LAIMINGESNI (yra tokių tyrimų). Galbūt todėl, kad prieš juos atsiveria daug daugiau galimybių ir gyvenimas tampa šviesesnis? nezinau...

Bet pagalvok pats...

Ko reikia, kad būtumėte tikri, kad vieningo valstybinio egzamino metu būtumėte geresni už kitus ir galiausiai būtumėte... laimingesni?

ĮGYKITE SAVO RANKĄ SPRĘSDAMI ŠIOS TEmos problemas.

Per egzaminą teorijos neprašys.

Jums reikės spręsti problemas prieš laiką.

Ir, jei jų neišsprendėte (DAUG!), tikrai kur nors padarysite kvailą klaidą arba tiesiog neturėsite laiko.

Tai kaip sporte – reikia kartoti daug kartų, kad laimėtum užtikrintai.

Raskite kolekciją, kur tik norite, būtinai su sprendimais, detalia analize ir nuspręsk, nuspręsk, nuspręsk!

Galite naudoti mūsų užduotis (neprivaloma) ir mes, žinoma, jas rekomenduojame.

Kad galėtumėte geriau atlikti užduotis, turite padėti pratęsti šiuo metu skaitomo YouClever vadovėlio galiojimo laiką.

Kaip? Yra dvi parinktys:

1. Atrakinkite visas paslėptas užduotis šiame straipsnyje -
2. Atrakinkite prieigą prie visų paslėptų užduočių visuose 99 vadovėlio straipsniuose - Pirkite vadovėlį - 899 RUR

Taip, mūsų vadovėlyje yra 99 tokie straipsniai ir iš karto galima atidaryti visas užduotis ir visus paslėptus tekstus.

Prieiga prie visų paslėptų užduočių suteikiama VISĄ svetainės gyvenimą.

Apibendrinant...

Jei jums nepatinka mūsų užduotys, susiraskite kitus. Tiesiog nesustokite ties teorija.

„Supratau“ ir „aš galiu išspręsti“ yra visiškai skirtingi įgūdžiai. Jums reikia abiejų.

Raskite problemas ir jas spręskite!

Šiame straipsnyje kalbėsime apie tiesės ir plokštumos statmenumą. Pirmiausia pateikiamas statmenos plokštumai linijos apibrėžimas, pateikiama grafinė iliustracija ir pavyzdys bei pavaizduotas plokštumai statmenos linijos žymėjimas. Po to suformuluojamas tiesės ir plokštumos statmenumo ženklas. Toliau gaunamos sąlygos, leidžiančios įrodyti tiesės ir plokštumos statmenumą, kai tiesė ir plokštuma nurodomos tam tikromis lygtimis stačiakampėje koordinačių sistemoje trimatėje erdvėje. Pabaigoje pateikiami išsamūs tipinių pavyzdžių ir problemų sprendimai.

Puslapio naršymas.

Statmena tiesė ir plokštuma – pagrindinė informacija.

Rekomenduojame pirmiausia pakartoti statmenų tiesių apibrėžimą, nes plokštumai statmenos linijos apibrėžimas pateikiamas per tiesių statmenumą.

Apibrėžimas.

Jie taip sako linija yra statmena plokštumai, jei jis statmenas bet kuriai šioje plokštumoje esančiai tiesei.

Taip pat galime sakyti, kad plokštuma yra statmena tiesei, arba tiesė ir plokštuma yra statmenos.

Norėdami nurodyti statmenumą, naudokite piktogramą, pvz., „“. Tai yra, jei linija c yra statmena plokštumai, galime trumpai parašyti .

Plokštumai statmenos linijos pavyzdys yra linija, išilgai kurios susikerta dvi gretimos kambario sienos. Ši linija yra statmena plokštumai ir lubų plokštumai. Lynas sporto salėje taip pat gali būti laikomas tiesios linijos atkarpa, statmena grindų plokštumai.

Baigdami šią straipsnio pastraipą pažymime, kad jei tiesė yra statmena plokštumai, tada kampas tarp tiesės ir plokštumos laikomas lygiu devyniasdešimt laipsnių.

Tiesės ir plokštumos statmenumas – statmenumo ženklas ir sąlygos.

Praktikoje dažnai kyla klausimas: „Ar duota tiesė ir plokštuma yra statmenos? Norėdami atsakyti į tai, yra pakankama tiesės ir plokštumos statmenumo sąlyga, tai yra sąlyga, kurios įvykdymas garantuoja tiesės ir plokštumos statmenumą. Ši pakankama sąlyga vadinama tiesės ir plokštumos statmenumo ženklu. Suformuluokime jį teoremos forma.

Teorema.

Kad tam tikra tiesė ir plokštuma būtų statmenos, pakanka, kad linija būtų statmena dviem susikertančioms tiesėms, esančioms šioje plokštumoje.

Tiesės ir plokštumos statmenumo ženklo įrodymą galite pasižiūrėti 10-11 klasių geometrijos vadovėlyje.

Sprendžiant tiesės ir plokštumos statmenumo nustatymo uždavinius, taip pat dažnai naudojama tokia teorema.

Teorema.

Jei viena iš dviejų lygiagrečių tiesių yra statmena plokštumai, tai antroji tiesė taip pat yra statmena plokštumai.

Mokykloje svarstoma daug uždavinių, kurių sprendimui naudojamas tiesės ir plokštumos statmenumo ženklas bei paskutinė teorema. Prie jų čia nesigilinsime. Šioje straipsnio dalyje daugiausia dėmesio skirsime šios būtinos ir pakankamos tiesės ir plokštumos statmenumo sąlygos taikymui.

Šią sąlygą galima perrašyti tokia forma.

Leisti yra tiesės a krypties vektorius ir yra normalusis plokštumos vektorius. Kad tiesė a ir plokštuma būtų statmenos, būtina ir pakanka to Ir : , kur t yra tikrasis skaičius.

Šios būtinos ir pakankamos tiesės ir plokštumos statmenumo sąlygos įrodymas grindžiamas tiesės krypties vektoriaus ir plokštumos normaliojo vektoriaus apibrėžimais.

Akivaizdu, kad šią sąlygą patogu naudoti tiesės ir plokštumos statmenumui įrodyti, kai galima nesunkiai rasti tiesės krypties vektoriaus koordinates ir plokštumos normaliojo vektoriaus koordinates fiksuotoje trimatėje erdvėje. . Tai pasakytina apie tuos atvejus, kai pateikiamos taškų, per kuriuos eina plokštuma ir tiesė, koordinatės, taip pat tais atvejais, kai tiesė nustatoma pagal kai kurias erdvės tiesės lygtis, o plokštuma suteikiama lygtimi tam tikro tipo lėktuvas.

Pažvelkime į kelių pavyzdžių sprendimus.

Pavyzdys.

Įrodykite tiesės statmenumą ir lėktuvai.

Sprendimas.

Žinome, kad erdvėje esančios tiesės kanoninių lygčių vardikliuose esantys skaičiai yra atitinkamos šios tiesės krypties vektoriaus koordinatės. Taigi, - tiesioginis vektorius .

Kintamųjų x, y ir z koeficientai bendrojoje plokštumos lygtyje yra šios plokštumos normaliojo vektoriaus koordinatės, t. yra normalusis plokštumos vektorius.

Patikrinkime būtinosios ir pakankamos tiesės ir plokštumos statmenumo sąlygos įvykdymą.

Nes , tada vektoriai ir yra susiję ryšiu , tai yra, jie yra kolineariniai. Todėl tiesiai statmenai plokštumai.

Pavyzdys.

Ar linija statmena? ir lėktuvas.

Sprendimas.

Raskime duotosios tiesės krypties vektorių ir plokštumos normalųjį vektorių, kad patikrintume, ar tenkinama būtina ir pakankama tiesės ir plokštumos statmenumo sąlyga.

Nukreipimo vektorius yra tiesus yra

2 vaizdo pamoka: Trijų statmenų teorema. Teorija

3 vaizdo pamoka: Trijų statmenų teorema. Užduotis

Paskaita: Tiesės ir plokštumos statmena, ženklai ir savybės; statmenas ir įstrižas; trijų statmenų teorema

Tiesės ir plokštumos statmena

Prisiminkime, kas yra tiesių linijų statmenumas. Linijos, kurios susikerta 90 laipsnių kampu, yra statmenos. Šiuo atveju kampas tarp jų gali būti arba susikirtimo tam tikru tašku atveju, arba perėjimo atveju. Jei kai kurios tiesės susikerta stačiu kampu, tada jas taip pat galima vadinti statmenomis, jei dėl lygiagretaus vertimo tiesė perkeliama į antrosios tiesės tašką.

Apibrėžimas: Jei tiesė yra statmena bet kuriai tiesei, kuri priklauso plokštumai, tada ji gali būti laikoma statmena šiai plokštumai.

Ženklas: Jei tam tikroje plokštumoje yra dvi statmenos tiesės ir kiekvienai iš jų yra statmena kokia nors trečia tiesė, tai ši trečioji tiesė yra statmena plokštumai.

Savybės:

• Jei kai kurios tiesės yra statmenos vienai plokštumai, tada jos yra lygiagrečios viena kitai.

• Jei yra dvi lygiagrečios plokštumos, taip pat tam tikra tiesė, kuri yra statmena vienai iš plokštumų, tai ji taip pat yra statmena antrajai.
• Galima daryti ir priešingą teiginį: jei tam tikra tiesė yra statmena dviem skirtingoms plokštumoms, tai tokios plokštumos būtinai yra lygiagrečios.

Pasviręs

Jei kokia nors tiesė jungia savavališką tašką, kuris nėra plokštumoje, su jokiu plokštumos tašku, tada tokia tiesė bus vadinama linkęs.

Atkreipkite dėmesį, kad jis yra pasviręs tik tada, kai kampas tarp jo ir plokštumos nėra 90 laipsnių.

Paveiksle AB yra pasvirusi į α plokštumą. Šiuo atveju taškas B vadinamas pasvirusio pagrindu.

Jei nuo taško A iki plokštumos nubrėžsime atkarpą, kuri su plokštuma sudarys 90 laipsnių kampą, tai ši atkarpa bus vadinama statmena. Statmenas taip pat vadinamas trumpiausiu atstumu iki plokštumos.

AC yra statmenas, nubrėžtas iš taško A į plokštumą α. Šiuo atveju taškas C vadinamas statmens pagrindu.

Jei šiame brėžinyje nubraižysime atkarpą, kuri sujungs statmens (C) pagrindą su pasvirusio (B) pagrindu, tada gauta atkarpa bus vadinama projekcija.

Paprastų konstrukcijų dėka gavome stačią trikampį. Šiame trikampyje kampas ABC vadinamas kampu tarp įstrižainės ir projekcijos.

Trijų statmenų teorema

Apibrėžimas. Tiesioji susikertanti plokštuma vadinama statmena šiai plokštumai, jei ji yra statmena bet kuriai tiesei, kuri yra duotoje plokštumoje ir eina per susikirtimo tašką.
Pasirašyti tiesės ir plokštumos statmena. Jei tiesė yra statmena dviem susikertančioms plokštumos tiesėms, tai ji yra statmena tai plokštumai.
Įrodymas. Leisti A– tiesi linija, statmena tiesioms linijoms b Ir Su priklausantis lėktuvui a. A yra linijų susikirtimo taškas. Lėktuve a nubrėžkite tiesią liniją per tašką A d, nesutampančias su tiesiomis linijomis b Ir Su. Dabar lėktuve a padarykime tiesioginį k, susikertančios linijos d Ir Su o ne per tašką A. Susikirtimo taškai yra atitinkamai D, B ir C. Nubraižykime jį tiesėje A skirtingomis kryptimis nuo taško A yra vienodos atkarpos AA 1 ir AA 2. Trikampis A 1 CA 2 yra lygiašonis, nes aukštis AC taip pat yra mediana (1 požymis), t.y. A 1 C = CA 2. Panašiai ir trikampyje A 1 BA 2 kraštinės A 1 B ir BA 2 yra lygios. Todėl trikampiai A 1 BC ir A 2 BC yra lygūs pagal trečiąjį kriterijų, todėl kampai A 1 BC ir A 2 BC yra lygūs. Tai reiškia, kad trikampiai A 1 BD ir A 2 BD yra lygūs pagal pirmąjį kriterijų. Todėl A 1 D ir A 2 D. Vadinasi, trikampis A 1 DA 2 pagal apibrėžimą yra lygiašonis. Lygiašoniame trikampyje A 1 D A 2 D A yra mediana (pagal konstrukciją), taigi ir aukštis, ty kampas A 1 AD yra tiesus, taigi tiesi linija A statmena tiesei linijai d. Taigi galima įrodyti, kad tiesi linija A statmena bet kuriai per tašką A kertančiai tiesei, priklausančiai plokštumai a. Iš apibrėžimo matyti, kad tiesi linija A statmenai plokštumai a.

Statyba tiesė, statmena nurodytai plokštumai iš taško, paimto už šios plokštumos.
Leisti a- plokštuma, A – taškas, nuo kurio reikia nuleisti statmeną. Plokštumoje nubrėžkime tiesią liniją A. Per tašką A ir tiesią liniją A nupieškime plokštumą b(tiesi linija ir taškas apibrėžia plokštumą, ir tik viena). Lėktuve b iš taško A nuleidžiame į tiesią A statmenas AB. Iš taško B į lėktuvą a Atkurkime statmeną ir nurodykime tiesę, ant kurios yra šis statmuo Su. Per atkarpą AB ir tiesę Su nupieškime plokštumą g(dvi susikertančios linijos apibrėžia plokštumą ir tik viena). Lėktuve g iš taško A nuleidžiame į tiesią Su statmenai AC. Įrodykime, kad atkarpa AC yra statmena plokštumai b. Įrodymas. Tiesiai A statmenos tiesioms linijoms Su ir AB (pagal konstrukciją), o tai reiškia, kad jis yra statmenas pačiai plokštumai g, kurioje yra šios dvi susikertančios tiesės (remiantis tiesės ir plokštumos statmenu). Ir kadangi jis yra statmenas šiai plokštumai, tai jis yra statmenas bet kuriai tiesei šioje plokštumoje, vadinasi, tai yra tiesi A statmenai AC. Tiesė AC yra statmena dviem tiesėms, esančioms plokštumoje α: Su(pagal konstrukciją) ir A(pagal tai, kas buvo įrodyta), reiškia, kad jis yra statmenas plokštumai α (remiantis tiesės ir plokštumos statmenumu)

1 teorema . Jei dvi susikertančios tiesės yra lygiagrečios dviem statmenoms tiesėms, tada jos taip pat yra statmenos.
Įrodymas. Leisti A Ir b- statmenos linijos, A 1 ir b 1 - joms lygiagrečios susikertančios linijos. Įrodykime, kad tiesios linijos A 1 ir b 1 yra statmenos.
Jei tiesiai A, b, A 1 ir b 1 yra toje pačioje plokštumoje, tada jie turi teoremoje nurodytą savybę, kaip žinoma iš planimetrijos.
Tarkime, kad mūsų linijos nėra toje pačioje plokštumoje. Tada tiesiai A Ir b yra tam tikroje plokštumoje α, o tiesės A 1 ir b 1 - kokioje nors plokštumoje β. Remiantis plokštumų lygiagretumu, plokštumos α ir β yra lygiagrečios. Tegul C yra tiesių susikirtimo taškas A Ir b, o C 1 - tiesių sankirtos A 1 ir b 1 . Nubrėžkime lygiagrečių tiesių plokštumą A Ir A A Ir A 1 taškuose A ir A 1. Lygiagrečių tiesių plokštumoje b Ir b 1 linija, lygiagreti tiesei CC 1. Ji peržengs linijas b Ir b 1 taškuose B ir B 1.
Keturkampiai CAA 1 C 1 ir SVV 1 C 1 yra lygiagretainiai, nes jų priešingos kraštinės lygiagrečios. Keturkampis ABC 1 A 1 taip pat yra lygiagretainis. Jo kraštinės AA 1 ir BB 1 lygiagrečios, nes kiekviena iš jų lygiagreti tiesei CC 1. Taigi keturkampis yra plokštumoje, einančioje per lygiagrečias tieses AA 1 ir BB 1. Ir jis kerta lygiagrečias plokštumas α ir β išilgai lygiagrečių tiesių AB ir A 1 B 1.
Kadangi lygiagretainio priešingos kraštinės yra lygios, tai AB = A 1 B 1, AC = A 1 C 1, BC = B 1 C 1. Pagal trečiąjį lygybės ženklą trikampiai ABC ir A 1 B 1 C 1 yra lygūs. Taigi kampas A 1 C 1 B 1, lygus kampui ACB, yra tiesus, t.y. tiesiai A 1 ir b 1 yra statmenos. ir kt.

Savybės statmena tiesei ir plokštumai.
2 teorema . Jei plokštuma yra statmena vienai iš dviejų lygiagrečių tiesių, tai ji taip pat yra statmena ir kitai.
Įrodymas. Leisti A 1 ir A 2 – dvi lygiagrečios tiesės ir α – tiesei statmena plokštuma A 1 . Įrodykime, kad ši plokštuma yra statmena tiesei A 2 .
Nubrėžkime 2 linijos per tašką A sankirtas A 2 su plokštuma α savavališka tiesė Su 2 α plokštumoje. Plokštumoje α per tašką A 1 nubrėžkime tiesės sankirtą A 1 su plokštuma α tiesia Su 1 lygiagrečiai linijai Su 2. Kadangi jis yra tiesus A 1 yra statmena plokštumai α, tada tiesios linijos A 1 ir Su 1 yra statmenos. O pagal 1 teoremą joms lygiagrečios susikertančios tiesės A 2 ir Su 2 taip pat yra statmenos. Taigi, tiesiai A 2 yra statmena bet kuriai linijai Su 2 α plokštumoje. Ir tai reiškia, kad tiesiai A 2 yra statmena plokštumai α. Teorema įrodyta.

3 teorema . Dvi tiesės, statmenos tai pačiai plokštumai, yra lygiagrečios viena kitai.
Turime plokštumą α ir dvi jai statmenas tieses A Ir b. Įrodykime tai A || b.
Per plokštumos tiesių susikirtimo taškus nubrėžkite tiesią liniją Su. Remdamiesi charakteristika, kurią gauname A ^ c Ir b ^ c. Per tiesias linijas A Ir b Nubraižykime plokštumą (dvi lygiagrečios tiesės apibrėžia plokštumą ir tik viena). Šioje plokštumoje turime dvi lygiagrečias tieses A Ir b ir sekantas Su. Jei vidinių vienpusių kampų suma yra 180°, tai linijos yra lygiagrečios. Turime kaip tik tokį atvejį – du stačius kampus. Štai kodėl A || b.

Nuolat matome, kad statmenai tai pačiai plokštumai yra lygiagretūs. Pavyzdžiui, vertikalūs segmentai yra lygiagrečiai vienas kitam. Šiuos segmentus gali pavaizduoti lygiagrečiai statomi stulpai ar stiebai, lieknų pušų kamienai laivų miške, muziejaus pastatų kolonos (84 pav.) ar vertikalios tilto atramos ir kt.

Ryžiai. 84

Ši elegantiška geometrija išreiškiama teorema, kurią dabar įrodysime.

8.1 Vienai plokštumai statmenų tiesių lygiagretumas

Įrodymas. Tegul dvi tiesės a ir b yra statmenos plokštumai a ir kerta ją atitinkamai taškuose A ir B (85 pav.). Per tiesę a ir tašką B nubrėžkime plokštumą p ir parodykime, kad tiesė b taip pat yra plokštumoje β.

Ryžiai. 85

Plokštumoje a paimkite atkarpą MN, statmeną atkarpai AB ir kurios taškas A yra jos vidurio taškas. Kadangi AM = AN ir AB ⊥ MN, tai BM = BN.

Paimkite bet kurį tašką C ≠ B tiesėje b ir nubrėžkite atkarpas CA, CM, CN. Kadangi b ⊥ a, tai trikampiai CBM ir CBN yra stačiakampiai. Jie yra lygūs, nes turi bendrą CB pusę ir lygias puses BM ir BN. Todėl CM = CN, ty trikampis CMN yra lygiašonis. Vidutinė jo CA taip pat yra jo aukštis, t. y. CA ⊥ MN.

Taigi trys tiesės, einančios per tašką A - AC, AB ir a - yra statmenos tiesei MN. Pagal teoremą apie statmenų plokštumą (7.2 skirsnis) jie guli toje pačioje plokštumoje – plokštumoje β, kuri eina per tieses AB ir a.

Kadangi tiesė AC yra plokštumoje β, tai taškas C ∈ β. Tai reiškia, kad tiesė b yra β plokštumoje (kaip tiesė a). Bet plokštumoje β tiesės a ir b yra statmenos tai pačiai tiesei AB (kadangi a ⊥ α, tada b ⊥ α ir tiesė AB yra α). Todėl b||a.

Įrodyta teorema yra tiesių lygiagretumo erdvėje ženklas.

8.2 Lygiagretus statmenai

Šiame skyriuje įrodysime teoremą, priešingą statmenų lygiagretumo teoremai.

Įrodymas. Tegul dvi tiesės a ir b yra lygiagrečios, o a statmenos plokštumai a (86 pav.). Tiesė b kerta plokštumą α tam tikrame taške B (pagal 3.3 lemą). Yra dvi galimybės:

1. b ⊥ α;
2. b nėra statmenas α.

Ryžiai. 86

Tarkime, kad veikia antrasis. Tada per tašką B nubrėžiame liniją su ⊥ α (7.3 uždavinio skyrius). Pagal teoremą apie statmenų lygiagretumą su||α. Pasirodo, kad per tašką B yra dvi tiesės, lygiagrečios tiesei A, o tai neįmanoma.

Taigi b ⊥ α.

Lygiagreti statmenai teorema yra dar vienas tiesės ir plokštumos statmenumo ženklas.

Klausimai savikontrolei

1. Kokius lygiagrečių tiesių ženklus išmokote?
2. Kokius tiesės ir plokštumos statmenumo ženklus dabar žinote?