يمكن تعريف الوظيفة بعدة طرق. يعتمد ذلك على القاعدة التي يتم استخدامها عند تعيينها. الشكل الصريح لتعريف الوظيفة هو y = f (x). هناك حالات يكون فيها وصفها مستحيلاً أو غير مريح. إذا كانت هناك مجموعة من الأزواج (x ؛ y) التي يجب حسابها للمعامل t خلال الفاصل الزمني (أ ؛ ب). لحل النظام x = 3 cos t y = 3 sin t مع 0 ≤ t< 2 π необходимо задавать окружность с центром координат с радиусом равным 3 .

تعريف الدالة البارامترية

ومن ثم لدينا أن x = φ (t) ، y = ψ (t) يتم تعريفها للقيمة t ∈ (a ؛ b) ولدينا دالة عكسية t = Θ (x) لـ x = φ (t) ، ثم نحن نتحدث عن وضع معادلة بارامترية لوظيفة بالصيغة y = ψ (Θ (x)).

هناك حالات عندما يكون من الضروري ، من أجل دراسة دالة ، البحث عن المشتق فيما يتعلق بـ x. ضع في اعتبارك صيغة مشتق دالة معطاة حدوديًا للصيغة y x "= ψ" (t) φ "(t) ، فلنتحدث عن مشتق من الرتبتين الثانية والنونية.

اشتقاق صيغة مشتق دالة معلمية معينة

لدينا أن x = φ (t) ، y = ψ (t) ، محدد وقابل للتفاضل لـ t ∈ a ؛ ب ، حيث x t "= φ" (t) ≠ 0 و x = φ (t) ، إذن هناك دالة عكسية للصيغة t = Θ (x).

بادئ ذي بدء ، يجب أن تنتقل من مهمة حدودية إلى مهمة صريحة. للقيام بذلك ، تحتاج إلى الحصول على دالة معقدة بالصيغة y = ψ (t) = ψ (Θ (x)) ، حيث توجد وسيطة x.

بناءً على قاعدة إيجاد مشتق دالة معقدة ، نحصل على y "x \ u003d ψ Θ (x) \ u003d ψ" Θ x Θ "x.

يوضح هذا أن t = Θ (x) و x = φ (t) هي دالات معكوسة من صيغة الدالة العكسية Θ "(x) = 1 φ" (t) ، ثم y "x = ψ" Θ (x) Θ " (س) = ψ "(ر) φ" (ر).

دعنا ننتقل إلى التفكير في حل عدة أمثلة باستخدام جدول المشتقات وفقًا لقاعدة الاشتقاق.

مثال 1

أوجد مشتق الدالة x = t 2 + 1 y = t.

المحلول

حسب الشرط ، لدينا φ (t) = t 2 + 1 ، ψ (t) = t ، ومن ثم نحصل على ذلك φ "(t) = t 2 + 1" ، ψ "(t) = t" = 1. من الضروري استخدام الصيغة المشتقة وكتابة الإجابة بالشكل:

y "x = ψ" (t) φ "(t) = 1 2 t

إجابه:ص س "= 1 2 ر س = ر 2 + 1.

عند العمل مع مشتق دالة ، تحدد المعلمة t التعبير عن الوسيطة x من خلال نفس المعلمة t حتى لا تفقد الاتصال بين قيم المشتق والدالة المحددة حدوديًا مع الوسيطة التي لها هذه تتوافق القيم.

لتحديد المشتق من الدرجة الثانية لوظيفة معينة حدوديًا ، تحتاج إلى استخدام صيغة مشتق الدرجة الأولى في الدالة الناتجة ، ثم نحصل على ذلك

y "" x = ψ "(t) φ" (t) "φ" (t) = ψ "" (t) φ "(t) - ψ" (t) φ "" (t) φ "(t) 2 φ "(t) = ψ" "(t) φ" (t) - ψ "(t) φ" "(t) φ" (t) 3.

مثال 2

أوجد المشتقات من الرتبة الثانية والثانية للدالة المعطاة x = cos (2 t) y = t 2.

المحلول

حسب الشرط ، نحصل على φ (t) = cos (2 t) ، ψ (t) = t 2.

ثم بعد التحول

φ "(t) \ u003d cos (2 t)" \ u003d - sin (2 t) 2 t "\ u003d - 2 sin (2 t) ψ (t) \ u003d t 2" \ u003d 2 t

ويترتب على ذلك أن y x "= ψ" (t) φ "(t) = 2 t - 2 sin 2 t = - t sin (2 t).

حصلنا على أن صيغة مشتق الرتبة الأولى هي x = cos (2 t) y x "= - t sin (2 t).

لحلها ، تحتاج إلى تطبيق صيغة مشتق من الدرجة الثانية. نحصل على تعبير مثل

y x "" \ u003d - t sin (2 t) φ "t \ u003d - t" sin (2 t) - t (sin (2 t)) "sin 2 (2 t) - 2 sin (2 t) = = 1 sin (2 t) - t cos (2 t) (2 t) "2 sin 3 (2 t) = sin (2 t) - 2 t cos (2 t) 2 sin 3 (2 t)

ثم قم بتعيين مشتق من الدرجة الثانية باستخدام الدالة البارامترية

x = cos (2 t) y x "" = sin (2 t) - 2 t cos (2 t) 2 sin 3 (2 t)

يمكن حل حل مماثل بطريقة أخرى. ثم

φ "t \ u003d (cos (2 t))" \ u003d - sin (2 t) 2 t "\ u003d - 2 sin (2 t) ⇒ φ" "t \ u003d - 2 sin (2 t)" \ u003d - 2 sin (2 t) "= - 2 cos (2 t) (2 t)" = - 4 cos (2 t) ψ "(t) = (t 2)" = 2 t ⇒ ψ "" (t) = (2 ر) "= 2

ومن ثم حصلنا على ذلك

y "" x = ψ "" (t) φ "(t) - ψ" (t) φ "" (t) φ "(t) 3 = 2 - 2 sin (2 t) - 2 t (- 4 cos (2 t)) - 2 sin 2 t 3 \ u003d \ u003d sin (2 t) - 2 t cos (2 t) 2 s i n 3 (2 t)

إجابه: y "" x \ u003d sin (2 t) - 2 t cos (2 t) 2 s i n 3 (2 t)

وبالمثل ، تم العثور على مشتقات ذات رتبة أعلى مع وظائف محددة حدوديًا.

إذا لاحظت وجود خطأ في النص ، فيرجى تمييزه والضغط على Ctrl + Enter

دعنا نفكر في تعريف الخط على المستوى ، حيث المتغيرات x ، y هي وظائف المتغير الثالث t (يسمى المعلمة):

لكل قيمة رمن بعض الفاصل الزمني تتوافق مع قيم معينة xو ذ و، ومن ثم نقطة معينة M (x ، y) من الطائرة. متي ريمر عبر جميع القيم من فاصل زمني معين ، ثم النقطة م (س ، ص) يصف بعض السطر إل. المعادلات (2.2) تسمى المعادلات البارامترية للخط إل.

إذا كانت الدالة x = φ (t) لها معكوس t = Ф (x) ، فعند استبدال هذا التعبير في المعادلة y = g (t) ، نحصل على y = g (Ф (x)) ، والتي تحدد ذك وضيفة من x. في هذه الحالة ، يُقال أن المعادلات (2.2) تحدد الوظيفة ذحدوديًا.

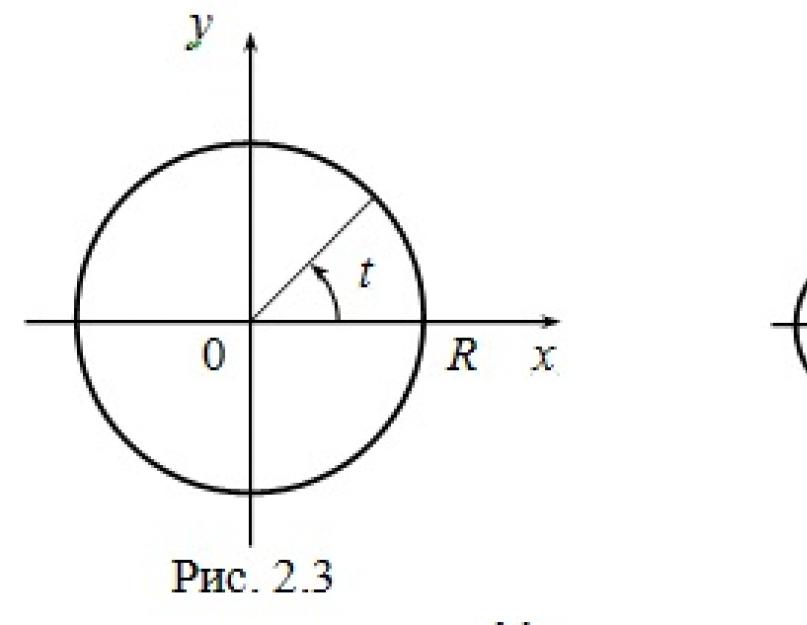
مثال 1يترك م (س ، ص)هي نقطة اعتباطية في دائرة نصف القطر صوتركزت في الأصل. يترك ر- الزاوية بين المحور ثورونصف القطر OM(انظر الشكل 2.3). ثم س ، صعبر ر:

المعادلات (2.3) هي معادلات حدودية للدائرة. دعونا نستبعد المعلمة t من المعادلات (2.3). للقيام بذلك ، نقوم بتربيع كل من المعادلات ونجمعها ، نحصل على: x 2 + y 2 \ u003d R 2 (cos 2 t + sin 2 t) أو x 2 + y 2 \ u003d R 2 - معادلة الدائرة في نظام الإحداثيات الديكارتية. تحدد وظيفتين: يتم إعطاء كل من هذه الوظائف بواسطة المعادلات البارامترية (2.3) ، ولكن للدالة الأولى ، وللثانية.

مثال 2. المعادلات البارامترية

تحديد القطع الناقص مع أنصاف المحاور أ ، ب(الشكل 2.4). حذف المعلمة من المعادلات ر، نحصل على المعادلة الأساسية للقطع الناقص:

مثال 3. الدائرة الحلقية عبارة عن خط موصوف بنقطة تقع على دائرة إذا كانت هذه الدائرة تدور دون أن تنزلق على طول خط مستقيم (الشكل 2.5). دعونا نقدم المعادلات البارامترية للدوران الدائري. دع نصف قطر الدائرة المتدحرجة يكون أ، نقطة م، واصفًا cycloid ، في بداية الحركة تزامنت مع الأصل.

دعونا نحدد الإحداثيات x، ص نقطة مبعد أن تدور الدائرة بزاوية ر
(الشكل 2.5) ، ر = ÐMCB. طول القوس ميغا بايتيساوي طول المقطع OB ،منذ أن الدائرة تدور دون انزلاق ، لذلك

OB = at ، AB = MD = asint ، CD = acost ، x = OB - AB = at - asint = a (t - sint) ،

y = AM = CB - CD = a - acost = a (1 - cost).

لذلك ، تم الحصول على المعادلات البارامترية للدوران الدائري:

عند تغيير المعلمة رمن 0 إلى 2πالدائرة تدور من خلال دورة واحدة ، بينما النقطة ميصف قوسًا من الدائرة الحلقية. تعريف المعادلات (2.5) ذك وضيفة من x. على الرغم من أن الوظيفة س = أ (تي - سينت)لها وظيفة عكسية ، ولكن لا يتم التعبير عنها من حيث الوظائف الأولية ، وبالتالي فإن الوظيفة ص = و (س)لا يتم التعبير عنها من حيث الوظائف الأولية.

ضع في اعتبارك اشتقاق الدالة المعطاة حدوديًا بواسطة المعادلات (2.2). الدالة x = φ (t) في فترة معينة من التغيير t لها دالة عكسية ر = Ф (س)، ومن بعد ص = ز (Ф (س)). يترك س = φ (ر), ص = ز (ر)لها مشتقات ، و x "t ≠ 0. حسب قاعدة اشتقاق دالة معقدة y "x = y" t × t "x.بناءً على قاعدة اشتقاق الدالة العكسية:

تسمح الصيغة الناتجة (2.6) للشخص بإيجاد المشتق لوظيفة معينة بشكل حدودي.

مثال 4. دع الوظيفة ذ، اعتمادا علي x، يتم تعيين حدودي:

المحلول. .
مثال 5ابحث عن المنحدر كمماس للدوران عند النقطة M 0 المقابلة لقيمة المعلمة.
المحلول.من المعادلات الدائرية: y "t = asint، x" t = a (1 - cost)،لهذا

منحدر ظل عند نقطة م 0يساوي القيمة عند ر 0 \ u003d π / 4:

وظيفة تفاضلية

دع الوظيفة عند نقطة ما × 0له مشتق. حسب التعريف:
لذلك ، من خلال خصائص الحد (ثانية. 1.8) ، حيث أصغير بشكل لا نهائي في ∆x → 0. من هنا

Δy = f "(x0) Δx + α × Δx. (2.7)

مثل Δx → 0 ، فإن المصطلح الثاني في المساواة (2.7) هو ترتيب أعلى متناهي الصغر ، بالمقارنة مع ، لذلك Δy و f "(x 0) × Δx متكافئان ، متناهي الصغر (لـ f" (x 0) ≠ 0).

وبالتالي ، فإن زيادة الدالة Δy تتكون من فترتين ، أولهما f "(x 0) × Δx هو الجزء الرئيسي الزيادات Δy ، الخطية بالنسبة إلى Δx (لـ f "(x 0) ≠ 0).

التفاضليهتسمى الوظيفة f (x) عند النقطة x 0 بالجزء الرئيسي من زيادة الوظيفة ويشار إليها: دىأو مدافع (x0). بالتالي،

df (x0) = f "(x0) × Δx. (2.8)

مثال 1أوجد تفاضل التابع دىوزيادة الدالة Δy للدالة y \ u003d x 2 عندما:
1) تعسفي xو Δ x؛ 2) × 0 \ u003d 20 ، Δx \ u003d 0.1.

المحلول

1) Δy \ u003d (x + Δx) 2 - x 2 \ u003d x 2 + 2xΔx + (Δx) 2 - x 2 \ u003d 2xΔx + (Δx) 2، dy \ u003d 2xΔx.

2) إذا كانت x 0 \ u003d 20 ، Δx \ u003d 0.1 ، ثم Δy \ u003d 40 × 0.1 + (0.1) 2 \ u003d 4.01 ؛ دى = 40 × 0.1 = 4.

نكتب المساواة (2.7) بالشكل:

Δy = dy + a × Δx. (2.9)

تختلف الزيادة عن التفاضل دىإلى ترتيب أعلى متناهي الصغر ، مقارنة بـ x ، لذلك ، في الحسابات التقريبية ، يتم استخدام المساواة التقريبية Δy ≈ dy إذا كانت x صغيرة بدرجة كافية.

بالنظر إلى أن Δy \ u003d f (x 0 + Δx) - f (x 0) ، نحصل على صيغة تقريبية:

و (x 0 + Δx) ≈ f (x 0) + dy. (2.10)

مثال 2. حساب تقريبا.

المحلول.انصح:

باستخدام الصيغة (2.10) ، نحصل على:

ومن ثم ، ≈ 2.025.

ضع في اعتبارك المعنى الهندسي للتفاضل مدافع (x0)(الشكل 2.6).

ارسم ظلًا للرسم البياني للدالة y = f (x) عند النقطة M 0 (x0، f (x 0)) ، دع φ تكون الزاوية بين الظل KM0 والمحور Ox ، ثم f "(x 0 ) = tgφ. من ΔM0NP:
PN \ u003d tgφ × Δx \ u003d f "(x 0) × Δx \ u003d df (x 0). لكن PN هي زيادة إحداثيات الظل عندما تتغير x من x 0 إلى x 0 + Δx.

لذلك ، فإن تفاضل الدالة f (x) عند النقطة x 0 يساوي الزيادة في إحداثيات المماس.

لنجد تفاضل الدالة
ص = س. بما أن (x) "= 1 ، إذن dx = 1 × Δx = Δx. نفترض أن تفاضل المتغير المستقل x يساوي زيادته ، أي dx = Δx.

إذا كانت x رقمًا عشوائيًا ، فمن خلال المساواة (2.8) نحصل على df (x) = f "(x) dx ، ومن أين .
وبالتالي ، فإن مشتق الدالة y = f (x) يساوي نسبة تفاضلها إلى تفاضل الوسيطة.

ضع في اعتبارك خصائص تفاضل الدالة.

إذا كانت u (x) ، v (x) دالات قابلة للتفاضل ، فإن الصيغ التالية صحيحة:

لإثبات هذه الصيغ ، يتم استخدام الصيغ المشتقة للمجموع والمنتج والحاصل. دعنا نثبت ، على سبيل المثال ، الصيغة (2.12):

د (u × v) = (u × v) "Δx = (u × v" + u "× v) Δx = u × v" Δx + u "Δx × v = u × dv + v × du.

ضع في اعتبارك تفاضل دالة معقدة: y = f (x) ، x = φ (t) ، أي ص = و (φ (ر)).

ثم dy = y "t dt ، لكن y" t = y "x × x" t ، لذا dy = y "x x" t dt. مع مراعاة،

أن x "t = dx ، نحصل على dy = y" x dx = f "(x) dx.

وبالتالي ، فإن تفاضل دالة معقدة y \ u003d f (x) ، حيث x \ u003d φ (t) ، لها الشكل dy \ u003d f "(x) dx ، كما هو الحال عندما يكون x متغيرًا مستقلاً. هذه الخاصية يسمى شكل تفاضلي ثابت أ.

حتى الآن ، درسنا معادلات الخطوط على المستوى ، والتي ترتبط ارتباطًا مباشرًا بالإحداثيات الحالية لنقاط هذه الخطوط. ومع ذلك ، غالبًا ما يتم استخدام طريقة أخرى لتحديد الخط ، حيث تعتبر الإحداثيات الحالية وظائف لمتغير ثالث.

دعونا نعطي وظيفتين للمتغير

تعتبر لنفس قيم t. ثم تتوافق أي من قيم t هذه مع قيمة معينة وقيمة معينة لـ y ، وبالتالي إلى نقطة معينة. عندما يمر المتغير t عبر جميع القيم من منطقة تعريف الوظيفة (73) ، تصف النقطة بعض السطر С في المستوى. تسمى المعادلات (73) المعادلات البارامترية لهذا الخط ، ويسمى المتغير معلمة.

افترض أن الوظيفة لها وظيفة عكسية ، واستبدال هذه الوظيفة في ثاني المعادلات (73) ، نحصل على المعادلة

معربا عن y كدالة

دعونا نتفق على القول بأن هذه الوظيفة تُعطى بشكل حدودي بواسطة المعادلات (73). الانتقال من هذه المعادلات إلى المعادلة (74) يسمى إزالة المعلمة. عند النظر في الوظائف المحددة حدوديًا ، فإن استبعاد المعلمة ليس ضروريًا فحسب ، بل ليس دائمًا ممكنًا عمليًا.

في كثير من الحالات ، يكون أكثر ملاءمة ، نظرًا للقيم المختلفة للمعامل ، حساب القيم المقابلة للوسيطة والوظيفة y باستخدام الصيغ (73).

ضع في اعتبارك الأمثلة.

مثال 1. لنكن نقطة اعتباطية لدائرة تتمحور حول الأصل ونصف القطر R. يتم التعبير عن الإحداثيات الديكارتية x و y لهذه النقطة من حيث نصف قطرها القطبي والزاوية القطبية ، والتي نشير إليها هنا بواسطة t ، على النحو التالي ( انظر الفصل الأول ، الفقرة 3 ، البند 3):

تسمى المعادلات (75) المعادلات البارامترية للدائرة. المعلمة فيها هي الزاوية القطبية ، والتي تختلف من 0 إلى.

إذا تم تربيع المعادلات (75) وإضافة مصطلح حسب المصطلح ، فبسبب الهوية ، سيتم حذف المعلمة وسيتم الحصول على معادلة الدائرة في نظام الإحداثيات الديكارتية ، والتي تحدد وظيفتين أساسيتين:

يتم تحديد كل من هذه الوظائف بشكل حدودي بواسطة المعادلات (75) ، لكن نطاقات اختلاف المعلمات لهذه الوظائف مختلفة. لأول واحد. الرسم البياني لهذه الوظيفة هو نصف الدائرة العلوي. بالنسبة للدالة الثانية ، يكون الرسم البياني الخاص بها هو نصف الدائرة السفلي.

مثال 2. النظر في القطع الناقص في نفس الوقت

ودائرة متمركزة في الأصل ونصف القطر أ (الشكل 138).

لكل نقطة M من القطع الناقص ، نربط النقطة N من الدائرة ، والتي لها نفس الحد الأقصى للنقطة M ، وتقع معها على نفس الجانب من محور الثور. يتم تحديد موضع النقطة N ، ومن ثم النقطة M ، تمامًا بواسطة الزاوية القطبية t للنقطة. في هذه الحالة ، بالنسبة للإحداثيات المشتركة ، نحصل على التعبير التالي: x \ u003d a. نجد الإحداثي عند النقطة M من معادلة القطع الناقص:

يتم اختيار العلامة لأن الإحداثي عند النقطة M والإحداثيات عند النقطة N يجب أن يكون لهما نفس العلامات.

وبالتالي ، يتم الحصول على المعادلات البارامترية التالية للقطع الناقص:

هنا تتغير المعلمة t من 0 إلى.

مثال 3. ضع في اعتبارك دائرة مركزها عند النقطة أ) ونصف قطرها أ ، والتي من الواضح أنها تلامس المحور x في الأصل (الشكل 139). افترض أن هذه الدائرة تدور دون انزلاق على المحور السيني. ثم النقطة M من الدائرة ، والتي تصادفت في اللحظة الأولى مع الأصل ، تصف خطًا يسمى دائريًا.

نشتق المعادلات البارامترية للدوران الدائري ، آخذين كمعامل t زاوية دوران الدائرة MSW عند نقل نقطتها الثابتة من الموضع O إلى الموضع M. ثم بالنسبة للإحداثيات و y للنقطة M نحصل على التعبيرات التالية:

نظرًا لحقيقة أن الدائرة تدور على طول المحور دون انزلاق ، فإن طول المقطع OB يساوي طول القوس VM. بما أن طول القوس VM يساوي حاصل ضرب نصف القطر a والزاوية المركزية t ، إذن. لهذا . لكن ، لذلك ،

هذه المعادلات هي المعادلات البارامترية للدوريات. عند تغيير المعلمة t من 0 إلى الدائرة ، ستحدث ثورة كاملة واحدة. ستصف النقطة M قوسًا واحدًا من الدائرة الحلقية.

يؤدي استبعاد المعامل t هنا إلى تعبيرات مرهقة وهو غير عملي عمليًا.

غالبًا ما يستخدم التعريف البارامترى للخطوط بشكل خاص في الميكانيكا ، ويلعب الوقت دور المعلمة.

مثال 4. لنحدد مسار قذيفة أطلقت من مسدس بسرعة ابتدائية بزاوية a في الأفق. يتم إهمال مقاومة الهواء وأبعاد المقذوفات ، باعتبار ذلك نقطة مادية.

دعنا نختار نظام إحداثيات. لأصل الإحداثيات ، نأخذ نقطة انطلاق المقذوف من الكمامة. دعنا نوجه محور الثور أفقيًا ، ومحور Oy - عموديًا ، ونضعهما في نفس المستوى مع فوهة البندقية. إذا لم تكن هناك قوة جاذبية ، فإن القذيفة ستتحرك على طول خط مستقيم وتصنع زاوية أ مع محور الثور ، وبحلول الوقت t تكون المقذوفة قد قطعت المسافة. بسبب جاذبية الأرض ، يجب أن ينخفض ​​المقذوف في هذه اللحظة عموديًا بقيمة. لذلك ، في الواقع ، في الوقت t ، يتم تحديد إحداثيات المقذوف بواسطة الصيغ:

هذه المعادلات ثوابت. عندما يتغير t ، ستتغير أيضًا إحداثيات نقطة مسار المقذوف. المعادلات هي معادلات بارامترية لمسار المقذوف ، حيث المعلمة هي الوقت

التعبير من المعادلة الأولى والاستبدال بها

المعادلة الثانية ، نحصل على معادلة مسار المقذوف بالصورة هذه هي معادلة القطع المكافئ.

مشتق دالة معطاة ضمنيًا.
مشتق من دالة محددة بارامتريا

في هذه المقالة ، سننظر في مهمتين نموذجيتين آخرتين غالبًا ما توجدان في اختبارات الرياضيات العليا. من أجل إتقان المادة بنجاح ، من الضروري أن تكون قادرًا على العثور على مشتقات على الأقل بمستوى متوسط. يمكنك تعلم كيفية العثور على المشتقات عمليًا من الصفر في درسين أساسيين و مشتق دالة مركبة. إذا كان كل شيء متوافقًا مع مهارات التمايز ، فلنبدأ.

مشتق من وظيفة محددة ضمنيًا

أو باختصار مشتق دالة ضمنية. ما هي الوظيفة الضمنية؟ لنتذكر أولاً تعريف دالة لمتغير واحد:

دالة لمتغير واحدهي القاعدة التي تقضي بأن كل قيمة للمتغير المستقل تتوافق مع قيمة واحدة فقط للدالة.

المتغير يسمى متغير مستقلأو جدال.
المتغير يسمى المتغير التابعأو وظيفة .

حتى الآن ، نظرنا في الوظائف المحددة في صريحشكل. ماذا يعني ذلك؟ دعونا نرتب لاستخلاص المعلومات على أمثلة محددة.

ضع في اعتبارك الوظيفة

نرى أنه على اليسار لدينا حرف "y" وحيد ، وعلى اليمين - س فقط. هذه هي الوظيفة صراحةمعبرا عنها من حيث المتغير المستقل.

دعنا نفكر في وظيفة أخرى:

هنا المتغيرات الموجودة "مختلطة". و مستحيل بأي شكل من الأشكالالتعبير عن "Y" فقط من خلال "X". ما هي هذه الطرق؟ نقل المصطلحات من جزء إلى جزء مع تغيير العلامة ، ووضع أقواس ، ورمي العوامل وفقًا لقاعدة التناسب ، وما إلى ذلك. أعد كتابة المساواة وحاول التعبير عن "y" صراحة :. يمكنك تحريف المعادلة وتقليبها لساعات ، لكنك لن تنجح.

اسمحوا لي أن أقدم: - مثال وظيفة ضمنية.

في سياق التحليل الرياضي ، ثبت أن الوظيفة الضمنية موجود(ولكن ليس دائمًا) ، يحتوي على رسم بياني (تمامًا مثل الوظيفة "العادية"). إنه نفس الشيء بالنسبة للدالة الضمنية. موجودالمشتق الأول ، المشتق الثاني ، إلخ. كما يقولون ، يتم احترام جميع حقوق الأقليات الجنسية.

وسنتعلم في هذا الدرس كيفية إيجاد مشتقة دالة معطاة ضمنيًا. إنها ليست بتلك الصعوبة! جميع قواعد التفاضل ، يبقى جدول مشتقات الدوال الأولية ساري المفعول. يكمن الاختلاف في نقطة غريبة واحدة ، والتي سننظر فيها الآن.

نعم ، وسأخبرك بالأخبار السارة - يتم تنفيذ المهام التي تمت مناقشتها أدناه وفقًا لخوارزمية صارمة وواضحة إلى حد ما دون حجر أمام ثلاثة مسارات.

مثال 1

1) في المرحلة الأولى ، نعلق السكتات الدماغية على كلا الجزأين:

2) نستخدم قواعد خطية المشتق (أول قاعدتين من الدرس كيف تجد المشتق؟ أمثلة الحل):

3) التمايز المباشر.
كيف نفرق ومفهومة تماما. ماذا تفعل حيث توجد "ألعاب" تحت الضربات؟

- فقط للعار ، مشتق الدالة يساوي مشتقها: .

كيف نفرق
لدينا هنا وظيفة معقدة. لماذا ا؟ يبدو أنه يوجد تحت شرط الجيب حرف واحد فقط "Y". لكن الحقيقة هي أن حرفًا واحدًا فقط "y" - هي وظيفة في حد ذاتها(انظر التعريف في بداية الدرس). وبالتالي ، فإن الجيب هو وظيفة خارجية ، وهي وظيفة داخلية. نستخدم قاعدة اشتقاق دالة معقدة :

المنتج قابل للتفاضل وفقًا للقاعدة المعتادة :

لاحظ أن هذه أيضًا دالة معقدة ، أي "لعبة ملتوية" هي وظيفة معقدة:

يجب أن يبدو تصميم الحل نفسه كما يلي:


إذا كانت هناك أقواس ، فافتحها:

4) على الجانب الأيسر ، نقوم بتجميع المصطلحات التي يوجد بها حرف "y" بخط. على الجانب الأيمن - ننقل كل شيء آخر:

5) على الجانب الأيسر ، نخرج المشتق من الأقواس:

6) ووفقًا لقاعدة التناسب ، نضع هذه الأقواس في مقام الجانب الأيمن:

تم العثور على المشتق. مستعد.

من المثير للاهتمام ملاحظة أنه يمكن إعادة كتابة أي دالة ضمنيًا. على سبيل المثال ، الوظيفة يمكن إعادة كتابتها على النحو التالي: . ونفرقها وفقًا للخوارزمية التي تم النظر فيها للتو. في الواقع ، تختلف عبارتا "وظيفة ضمنية" و "وظيفة ضمنية" في فارق بسيط دلالي واحد. عبارة "وظيفة محددة ضمنيًا" أكثر عمومية وصحيحة ، - هذه الوظيفة معطاة ضمنيًا ، ولكن هنا يمكنك التعبير عن "y" وتقديم الوظيفة بشكل صريح. تعني عبارة "وظيفة ضمنية" وظيفة ضمنية "كلاسيكية" ، عندما لا يمكن التعبير عن "y".

الطريقة الثانية لحلها

انتباه!يمكنك التعرف على الطريقة الثانية فقط إذا كنت تعرف كيف تجدها بثقة المشتقات الجزئية. مبتدئين في حساب التفاضل والتكامل والدمى من فضلك لا تقرأ ولا تتخطى هذه الفقرةوإلا فسيكون الرأس في حالة من الفوضى الكاملة.

أوجد مشتق التابع الضمني بالطريقة الثانية.

ننقل كل الشروط إلى الجانب الأيسر:

وفكر في دالة من متغيرين:

ثم يمكن إيجاد المشتق من خلال الصيغة
لنجد المشتقات الجزئية:

في هذا الطريق:

الحل الثاني يسمح لك بإجراء فحص. لكن من غير المرغوب فيه وضع نسخة نهائية من المهمة لهم ، حيث يتم إتقان المشتقات الجزئية لاحقًا ، ولا ينبغي للطالب الذي يدرس موضوع "مشتق دالة لمتغير واحد" أن يعرف المشتقات الجزئية.

لنلقِ نظرة على بعض الأمثلة الأخرى.

مثال 2

أوجد مشتق دالة معطاة ضمنيًا

نعلق السكتات الدماغية على كلا الجزأين:

نستخدم قواعد الخطية:

إيجاد المشتقات:

توسيع كل الأقواس:

ننقل جميع الشروط إلى الجانب الأيسر ، والباقي - إلى الجانب الأيمن:

الجواب النهائي:

مثال 3

أوجد مشتق دالة معطاة ضمنيًا

حل كامل وعينة تصميم في نهاية الدرس.

ليس من غير المألوف أن تظهر الكسور بعد التفاضل. في مثل هذه الحالات ، يجب التخلص من الكسور. لنلق نظرة على مثالين آخرين.

مثال 4

أوجد مشتق دالة معطاة ضمنيًا

نستنتج كلا الجزأين تحت السكتات الدماغية ونستخدم قاعدة الخطية:

نشتق باستخدام قاعدة اشتقاق دالة معقدة وقاعدة اشتقاق حاصل القسمة :

توسيع الأقواس:

الآن علينا التخلص من الكسر. يمكن القيام بذلك لاحقًا ، لكن من المنطقي فعل ذلك على الفور. مقام الكسر هو. تتضاعف على ال . بالتفصيل ، سيبدو كما يلي:

في بعض الأحيان بعد التفاضل ، تظهر 2-3 كسور. إذا كان لدينا كسر واحد ، على سبيل المثال ، فسيتعين تكرار العملية - الضرب كل مصطلح من كل جزءعلى ال

على الجانب الأيسر ، نضعه بين قوسين:

الجواب النهائي:

مثال 5

أوجد مشتق دالة معطاة ضمنيًا

هذا مثال على "افعل ذلك بنفسك". الشيء الوحيد الموجود فيه ، قبل التخلص من الكسر ، ستحتاج أولاً إلى التخلص من الهيكل المكون من ثلاثة طوابق للكسر نفسه. الحل الكامل والإجابة في نهاية الدرس.

مشتق من دالة محددة بارامتريا

لا تجهد ، في هذه الفقرة أيضًا ، كل شيء بسيط للغاية. يمكنك تدوين الصيغة العامة لوظيفة معينة بارامتراتيًا ، ولكن لتوضيح ذلك ، سأقوم على الفور بتدوين مثال محدد. في الصيغة البارامترية ، تُعطى الوظيفة من خلال معادلتين:. في كثير من الأحيان ، لا تتم كتابة المعادلات تحت الأقواس المتعرجة ، ولكن بالتتابع: ،.

المتغير يسمى المعلمةويمكن أن تأخذ القيم من "سالب اللانهاية" إلى "زائد اللانهاية". ضع في اعتبارك ، على سبيل المثال ، القيمة واستبدلها في كلتا المعادلتين: . أو بشريًا: "إذا كانت x تساوي أربعة ، فإن y تساوي واحدًا". يمكنك تحديد نقطة على مستوى الإحداثيات ، وستتوافق هذه النقطة مع قيمة المعلمة. وبالمثل ، يمكنك العثور على نقطة لأي قيمة للمعامل "te". أما بالنسبة للدالة "العادية" ، فبالنسبة للهنود الأمريكيين لوظيفة معينة حدوديًا ، يتم أيضًا احترام جميع الحقوق: يمكنك رسم رسم بياني ، والعثور على المشتقات ، وما إلى ذلك. بالمناسبة ، إذا كانت هناك حاجة لإنشاء رسم بياني لوظيفة معينة حدوديًا ، يمكنك استخدام برنامجي.

في أبسط الحالات ، من الممكن تمثيل الوظيفة بشكل صريح. نعبر عن المعلمة من المعادلة الأولى: واستبدله في المعادلة الثانية: . والنتيجة دالة تكعيبية عادية.

في الحالات "الشديدة" ، لا تنجح هذه الحيلة. لكن هذا لا يهم ، لأن هناك صيغة لإيجاد مشتق الدالة البارامترية:

نجد مشتق "اللاعب بالنسبة للمتغير te":

جميع قواعد التفاضل وجدول المشتقات صالحة بالطبع للحرف ، وبالتالي ، لا يوجد حداثة في عملية إيجاد المشتقات. فقط استبدل عقليًا جميع "x" في الجدول بالحرف "te".

نجد مشتق "x بالنسبة إلى المتغير te":

الآن يبقى فقط استبدال المشتقات الموجودة في صيغتنا:

مستعد. المشتق ، مثل الوظيفة نفسها ، يعتمد أيضًا على المعلمة.

أما بالنسبة للتدوين ، فبدلاً من كتابته في الصيغة ، يمكن للمرء ببساطة كتابته بدون رمز منخفض ، لأن هذا هو المشتق "العادي" "بواسطة x". لكن هناك دائمًا متغير في الأدبيات ، لذلك لن أحيد عن المعيار.

مثال 6

نستخدم الصيغة

في هذه الحالة:

في هذا الطريق:

ميزة إيجاد مشتق دالة حدودية هي حقيقة ذلك في كل خطوة ، من المفيد تبسيط النتيجة قدر الإمكان. لذلك ، في المثال المدروس ، عند البحث ، فتحت الأقواس الموجودة أسفل الجذر (على الرغم من أنني ربما لم أفعل ذلك). هناك فرصة كبيرة أنه عند الاستبدال وفي الصيغة ، سيتم تقليل أشياء كثيرة بشكل جيد. على الرغم من وجود ، بالطبع ، أمثلة ذات إجابات خرقاء.

مثال 7

أوجد مشتق دالة معطاة بارامترًا

هذا مثال على "افعل ذلك بنفسك".

في المقالة أبسط المشاكل النموذجية مع المشتقدرسنا الأمثلة التي كان مطلوبًا فيها إيجاد المشتق الثاني للدالة. بالنسبة للدالة المعطاة حدوديًا ، يمكنك أيضًا إيجاد المشتق الثاني ، ويمكن إيجاده بالصيغة التالية:. من الواضح تمامًا أنه لإيجاد المشتق الثاني ، يجب أولاً إيجاد المشتق الأول.

المثال 8

أوجد المشتقتين الأولى والثانية لدالة معطاة بارامترًا

لنجد المشتق الأول أولًا.
نستخدم الصيغة

في هذه الحالة:

نعوض بالمشتقات التي تم العثور عليها في الصيغة. من أجل البساطة ، نستخدم الصيغة المثلثية:

تم تعريف صيغة مشتق دالة بطريقة بارامترية. دليل وأمثلة لتطبيق هذه الصيغة. أمثلة على حساب المشتقات من الرتب الأول والثاني والثالث.

دع الوظيفة تعطى بطريقة حدودية:
(1)
أين يوجد متغير يسمى المعلمة. وليكن للدوال ومشتقاتها قيمة ما للمتغير. علاوة على ذلك ، فإن الوظيفة لها أيضًا وظيفة عكسية في بعض المناطق المجاورة للنقطة. ثم الوظيفة (1) لها مشتق عند النقطة ، والتي ، في شكل حدودي ، تحددها الصيغ:
(2)

هنا و هي مشتقات من الوظائف و فيما يتعلق بالمتغير (المعلمة). غالبًا ما يتم كتابتها بالشكل التالي:
;
.

ثم يمكن كتابة النظام (2) على النحو التالي:

دليل - إثبات

حسب الشرط ، فإن الوظيفة لها وظيفة عكسية. دعنا نشير إليها على أنها
.
ثم يمكن تمثيل الوظيفة الأصلية كدالة معقدة:
.
لنجد مشتقها من خلال تطبيق قواعد اشتقاق الدوال المعقدة والمعكوسة:
.

لقد تم إثبات القاعدة.

الإثبات في الطريقة الثانية

لنجد المشتق بالطريقة الثانية ، بناءً على تعريف مشتق الوظيفة عند النقطة:
.
دعنا نقدم الترميز:
.
ثم تأخذ الصيغة السابقة الشكل:
.

دعونا نستخدم حقيقة أن للدالة دالة عكسية بالقرب من النقطة.
دعونا نقدم التدوين:
; ;
; .
اقسم بسط الكسر ومقامه على:
.
في ، . ثم
.

لقد تم إثبات القاعدة.

مشتقات الطلبات الأعلى

للعثور على مشتقات من أوامر أعلى ، من الضروري إجراء التفاضل عدة مرات. لنفترض أننا بحاجة إلى إيجاد مشتق من الدرجة الثانية لوظيفة معينة بطريقة حدية ، بالشكل التالي:
(1)

وفقًا للصيغة (2) ، نجد المشتق الأول ، والذي يتم تحديده أيضًا بشكل حدودي:
(2)

أشر إلى المشتق الأول عن طريق متغير:
.
بعد ذلك ، لإيجاد المشتق الثاني للدالة بالنسبة إلى المتغير ، تحتاج إلى إيجاد المشتق الأول للدالة بالنسبة إلى المتغير. يتم أيضًا تحديد اعتماد المتغير على المتغير بطريقة حدودية:
(3)
بمقارنة (3) بالصيغتين (1) و (2) نجد:

الآن دعنا نعبر عن النتيجة بدلالة الدوال و. للقيام بذلك ، نعوض ونطبق صيغة مشتق الكسر:
.
ثم
.

من هنا نحصل على المشتق الثاني للدالة فيما يتعلق بالمتغير:

يتم تقديمها أيضًا في شكل حدودي. لاحظ أنه يمكن أيضًا كتابة السطر الأول على النحو التالي:
.

استمرارًا للعملية ، من الممكن الحصول على مشتقات الوظائف من متغير من الطلبات الثالثة والأعلى.

لاحظ أنه من الممكن عدم تقديم رمز المشتق. يمكن كتابتها على النحو التالي:
;
.

مثال 1

أوجد مشتق دالة معطاة بطريقة حدودية:

المحلول

نجد مشتقات و بالنسبة ل.
من جدول المشتقات نجد:
;
.
نطبق:

.
هنا .

.
هنا .

المشتق المطلوب:
.

إجابه

مثال 2

ابحث عن مشتق الوظيفة المعبر عنها من خلال المعلمة:

المحلول

لنفتح الأقواس باستخدام الصيغ لوظائف الطاقة والجذور:
.

نجد المشتق:

.

نجد المشتق. للقيام بذلك ، نقدم متغيرًا ونطبق صيغة مشتقة دالة معقدة.

.

نجد المشتق المطلوب:
.

إجابه

مثال 3

أوجد المشتقات الثانية والثالثة للدالة المعطاة حدوديًا في المثال 1:

المحلول

في المثال 1 وجدنا مشتق من الدرجة الأولى:

دعنا نقدم الترميز. ثم الوظيفة هي المشتق بالنسبة ل. يتم تعيينه حدوديًا:

لإيجاد المشتق الثاني بالنسبة إلى ، علينا إيجاد المشتق الأول بالنسبة إلى.

نحن نفرق فيما يتعلق.
.
وجدنا المشتق في المثال 1:
.
مشتق الرتبة الثانية فيما يتعلق بـ يساوي مشتق من الدرجة الأولى فيما يتعلق بـ:
.

إذن ، وجدنا المشتق من الدرجة الثانية فيما يتعلق بالصيغة البارامترية:

الآن نجد مشتقة الرتبة الثالثة. دعنا نقدم الترميز. ثم نحتاج إلى إيجاد المشتق الأول للدالة ، والذي يُعطى بطريقة حدية:

نجد المشتق بالنسبة ل. للقيام بذلك ، نعيد الكتابة في شكل مكافئ:
.
من

.

مشتق الرتبة الثالث فيما يتعلق بـ يساوي مشتق من الدرجة الأولى فيما يتعلق بـ:
.

تعليق

من الممكن عدم إدخال المتغيرات والتي هي مشتقات من و ، على التوالي. ثم يمكنك كتابتها على النحو التالي:
;
;
;
;
;
;
;
;
.

إجابه

في التمثيل البارامتري ، يكون للمشتق من الدرجة الثانية الشكل التالي:

مشتق من الدرجة الثالثة: