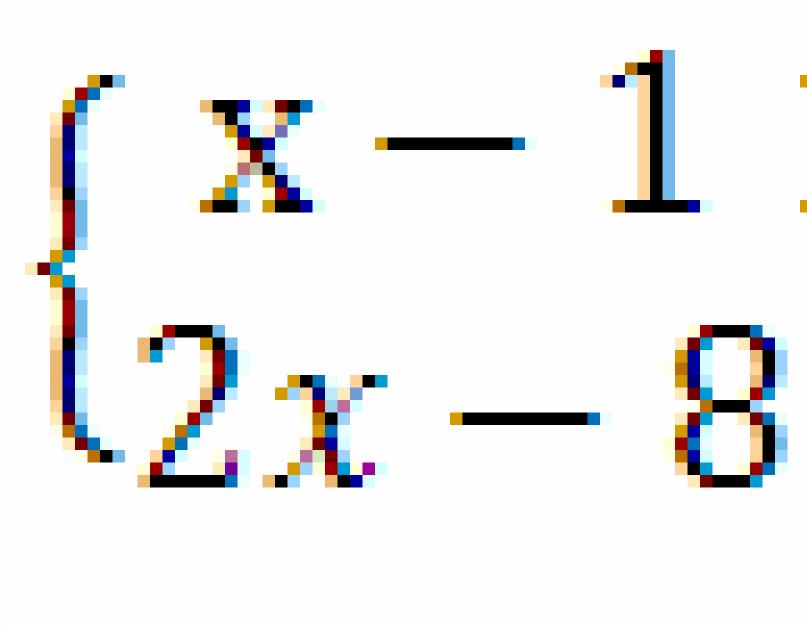Sistem nejednakosti Uobičajeno je da se naziva bilo koji skup od dvije ili više nejednačina koji sadrže nepoznatu količinu.

Ova formulacija je jasno ilustrovana, na primjer, takvim sistema nejednakosti:

Riješite sistem nejednačina - znači pronaći sve vrijednosti nepoznate varijable za koje se ostvaruje svaka nejednakost sistema ili dokazati da takve ne postoje .

Dakle, za svakog pojedinca sistemske nejednakosti izračunaj nepoznatu varijablu. Nadalje, iz rezultirajućih vrijednosti, odabire se samo one koje su istinite i za prvu i za drugu nejednakost. Dakle, prilikom zamjene odabrane vrijednosti obje nejednakosti sistema postaju tačne.

Analizirajmo rješenje nekoliko nejednačina:

Stavite jednu ispod drugog para brojevnih linija; stavite vrijednost na vrh x, pod kojom je prva nejednakost o ( x> 1) postaje istinito, a na dnu vrijednost X, koji su rješenje druge nejednačine ( X> 4).

Poređenjem podataka na brojevne linije, imajte na umu da je rješenje za oba nejednakosti bice X> 4. Odgovor, X> 4.

Primjer 2

Izračunavanje prvog nejednakost dobijamo -3 X< -6, или x> 2, drugi - X> -8, ili X < 8. Затем делаем по аналогии с предыдущим примером. На верхнюю числовую прямую наносим все те значения X, pod kojim je prvi sistemska nejednakost, a na donjoj brojevnoj liniji sve te vrijednosti X, pod kojim se ostvaruje druga nejednakost sistema.

Upoređujući podatke, nalazimo da oboje nejednakostiće se implementirati za sve vrijednosti X plasirani od 2 do 8. Skupovi vrijednosti X označiti dvostruka nejednakost 2 < X< 8.

Primjer 3 Hajde da nađemo

Nejednakosti i sistemi nejednakosti jedna su od tema koje se obrađuju srednja škola u algebri. Što se tiče težine, nije najteže, jer ima jednostavna pravila (o njima malo kasnije). Po pravilu, školarci vrlo lako uče rješavanje sistema nejednakosti. To je također zbog činjenice da nastavnici jednostavno "obučavaju" svoje učenike o ovoj temi. I to ne mogu a da ne rade, jer se to u budućnosti proučava uz korištenje drugih matematičkih veličina, a također se provjerava za OGE i Jedinstveni državni ispit. U školskim udžbenicima tema nejednakosti i sistema nejednakosti je detaljno obrađena, pa ako ćete je proučavati, onda je najbolje da im pribjegnete. Ovaj članak samo prepričava velike materijale, a u njemu može biti nekih propusta.

Koncept sistema nejednakosti

Ako se okrenemo naučnom jeziku, možemo definisati pojam "sistema nejednakosti". Ovo je takav matematički model, koji predstavlja nekoliko nejednakosti. Ovaj model, naravno, zahtijeva rješenje, a ono će biti opći odgovor za sve nejednakosti sistema predloženog u zadatku (obično se piše ovako, na primjer: "Riješi sistem nejednačina 4 x + 1 > 2 i 30 - x > 6..."). Međutim, prije nego što pređete na vrste i metode rješenja, morate razumjeti nešto drugo.

Sistemi nejednačina i sistemi jednačina

U procesu studiranja nova tema vrlo često dolazi do nesporazuma. S jedne strane sve je jasno i radije bih krenuo u rješavanje zadataka, ali s druge strane neki momenti ostaju u "sjeni", nisu dobro shvaćeni. Takođe, neki elementi već stečenog znanja mogu se preplitati sa novim. Kao rezultat ovog "preklapanja" često se javljaju greške.

Stoga, prije nego što pređemo na analizu naše teme, treba se prisjetiti razlika između jednačina i nejednačina, njihovih sistema. Da biste to učinili, morate još jednom objasniti koji su to matematički koncepti. Jednačina je uvijek jednakost i uvijek je nečemu jednaka (u matematici se ova riječ označava znakom "="). Nejednakost je model u kojem je jedna vrijednost ili veća ili manja od druge, ili sadrži tvrdnju da nisu iste. Tako je u prvom slučaju primjereno govoriti o jednakosti, a u drugom, koliko god očito zvučalo iz samog naziva, o nejednakosti početnih podataka. Sistemi jednačina i nejednačina se praktično ne razlikuju jedni od drugih, a metode za njihovo rješavanje su iste. Jedina razlika je u tome što prvi koristi jednakosti, dok drugi koristi nejednakosti.

Vrste nejednakosti

Postoje dvije vrste nejednakosti: numeričke i s nepoznatom promjenljivom. Prvi tip daje vrijednosti (brojeve) koje su međusobno nejednake, na primjer, 8 > 10. Drugi su nejednakosti koje sadrže nepoznatu varijablu (označene nekim slovom latinica, najčešće X). Ovu varijablu treba pronaći. U zavisnosti od toga koliko ih ima, matematički model razlikuje nejednakosti sa jednom (one čine sistem nejednakosti sa jednom promenljivom) ili više varijabli (oni čine sistem nejednakosti sa više varijabli).

Dva poslednja vrsta Prema stepenu izgrađenosti i stepenu složenosti rješenja se dijele na jednostavna i složena. Jednostavne se još nazivaju i linearne nejednačine. Oni se, pak, dijele na stroge i nestroge. Strogo posebno "recite" da jedna vrijednost mora nužno biti ili manja ili više, tako da je ovo in čista forma nejednakost. Postoji nekoliko primjera: 8 x + 9 > 2, 100 - 3 x > 5, itd. Nestrogi također uključuju jednakost. To jest, jedna vrijednost može biti veća ili jednaka drugoj vrijednosti (znak "≥") ili manja ili jednaka drugoj vrijednosti (znak "≤"). Čak iu linearnim nejednačinama varijabla ne stoji u korijenu, kvadratu, nije djeljiva ni sa čim, zbog čega se nazivaju "jednostavnim". Kompleksne uključuju nepoznate varijable, za čije pronalaženje je potrebno više matematičkih operacija. Često su u kvadratu, kocki ili ispod korena, mogu biti modularni, logaritamski, razlomci, itd. Ali pošto je naš zadatak da razumemo rešenje sistema nejednačina, govorićemo o sistemu linearnih nejednačina. Međutim, prije toga treba reći nekoliko riječi o njihovim svojstvima.

Svojstva nejednakosti

Svojstva nejednakosti uključuju sljedeće odredbe:

1. Predznak nejednakosti se obrće ako se primeni operacija promene redosleda strana (na primer, ako je t 1 ≤ t 2, onda t 2 ≥ t 1).
2. Oba dijela nejednakosti vam omogućavaju da sebi dodate isti broj (na primjer, ako je t 1 ≤ t 2, onda t 1 + broj ≤ t 2 + broj).
3. Dvije ili više nejednakosti koje imaju predznak istog smjera omogućavaju vam da dodate njihov lijevi i desni dio (na primjer, ako je t 1 ≥ t 2, t 3 ≥ t 4, tada t 1 + t 3 ≥ t 2 + t 4 ).
4. Oba dijela nejednakosti dozvoljavaju da se pomnože ili podijele sa istim pozitivnim brojem (na primjer, ako je t 1 ≤ t 2 i broj ≤ 0, tada je broj t 1 ≥ broj t 2).
5. Dvije ili više nejednakosti koje imaju pozitivne članove i znak istog smjera dopuštaju da se međusobno pomnože (na primjer, ako je t 1 ≤ t 2 , t 3 ≤ t 4 , t 1 , t 2 , t 3 , t 4 ≥ 0 tada t 1 t 3 ≤ t 2 t 4).
6. Oba dijela nejednakosti dopuštaju da se pomnože ili podijele istim negativan broj, ali se predznak nejednakosti mijenja (na primjer, ako je t 1 ≤ t 2 i broj ≤ 0, tada je broj t 1 ≥ broj t 2).
7. Sve nejednačine imaju svojstvo tranzitivnosti (na primjer, ako je t 1 ≤ t 2 i t 2 ≤ t 3, tada je t 1 ≤ t 3).

Sada, nakon proučavanja glavnih odredbi teorije vezanih za nejednakosti, možemo prijeći direktno na razmatranje pravila za rješavanje njihovih sistema.

Rješenje sistema nejednačina. Opće informacije. Rješenja

Kao što je gore spomenuto, rješenje su vrijednosti varijable koje odgovaraju svim nejednačinama datog sistema. Rješenje sistema nejednakosti je implementacija matematičke operacije, koji u konačnici dovode do rješenja cijelog sistema ili dokazuju da on nema rješenja. U ovom slučaju se kaže da se varijabla odnosi na prazan numerički skup (napisan ovako: slovo koje označava promenljivu∈ (znak "pripada") ø (znak "prazan skup"), na primjer, x ∈ ø (čita se: "Varijabla "x" pripada praznom skupu"). Postoji nekoliko načina za rješavanje sistema nejednačina: grafički, algebarski, zamjenski metod. Treba napomenuti da jesu matematički modeli, koji imaju nekoliko nepoznatih varijabli. U slučaju kada postoji samo jedan, prikladan je metod intervala.

Grafički način

Omogućava vam da riješite sistem nejednakosti sa nekoliko nepoznanica (od dvije ili više). Zahvaljujući ovoj metodi, sistem linearnih nejednačina se rešava prilično lako i brzo, tako da je to najčešća metoda. To je zato što crtanje smanjuje količinu pisanja matematičkih operacija. Postaje posebno ugodno malo predahnuti od olovke, uzeti olovku s ravnalom i uz njihovu pomoć nastaviti s daljnjim radnjama kada je puno posla obavljeno i želite malo raznolikosti. Međutim, neki ne vole ovu metodu zbog činjenice da morate da se odvojite od zadatka i promenite svoj mentalna aktivnost za crtanje. Međutim, to je veoma efikasan način.

Za rješavanje sistema nejednačina koristeći grafički način, potrebno je sve članove svake nejednakosti prenijeti na njihov lijeva strana. Predznaci će biti obrnuti, nula treba napisati na desnoj strani, a zatim svaka nejednakost treba biti napisana posebno. Kao rezultat, funkcije će se dobiti iz nejednakosti. Nakon toga možete dobiti olovku i ravnalo: sada morate nacrtati graf svake dobivene funkcije. Čitav skup brojeva koji će biti u intervalu njihovog preseka biće rešenje sistema nejednačina.

Algebarski način

Omogućava vam da riješite sistem nejednakosti sa dvije nepoznate varijable. Takođe, nejednakosti moraju postojati isti znak nejednakosti (odnosno, moraju sadržavati ili samo znak "veće od" ili samo znak "manje od" itd.) Uprkos svojim ograničenjima, ovaj metod je takođe komplikovaniji. Primjenjuje se u dvije faze.

Prvi uključuje radnje za uklanjanje jedne od nepoznatih varijabli. Prvo ga trebate odabrati, a zatim provjeriti prisustvo brojeva ispred ove varijable. Ako ih nema (tada će varijabla izgledati kao jedno slovo), onda ništa ne mijenjamo, ako postoji (tip varijable će biti npr. 5y ili 12y), onda je potrebno osigurati da je u svakoj nejednakosti broj ispred odabrane varijable isti. Da biste to učinili, trebate pomnožiti svaki član nejednakosti sa zajedničkim faktorom, na primjer, ako je 3y napisano u prvoj nejednakosti, a 5y u drugoj, tada morate pomnožiti sve članove prve nejednakosti sa 5 , a drugi za 3. Ispašće 15y i 15y respektivno.

Druga faza odluke. Potrebno je prenijeti lijevu stranu svake nejednačine na njihove desne strane s promjenom predznaka svakog člana na suprotno, na desnoj strani napisati nulu. Zatim dolazi zabavni dio: oslobađanje od odabrane varijable (inače poznate kao "redukcija") uz sabiranje nejednakosti. Dobićete nejednakost sa jednom promenljivom koju treba rešiti. Nakon toga treba da uradite isto, samo sa drugom nepoznatom promenljivom. Dobijeni rezultati će biti rješenje sistema.

Metoda zamjene

Omogućava vam da riješite sistem nejednakosti kada je moguće uvesti novu varijablu. Obično se ova metoda koristi kada se nepoznata varijabla u jednom članu nejednakosti podigne na četvrti stepen, a u drugom se kvadrira. Dakle, ovaj metod ima za cilj smanjenje stepena nejednakosti u sistemu. Nejednakost uzorka x 4 - x 2 - 1 ≤ 0 rješava se na sljedeći način. Uvodi se nova varijabla, na primjer t. Oni pišu: "Neka je t = x 2", a zatim se model prepisuje u novom obliku. U našem slučaju dobijamo t 2 - t - 1 ≤0. Ovu nejednakost treba riješiti intervalnom metodom (o tome malo kasnije), zatim se vratiti na varijablu X, a zatim učiniti isto s drugom nejednakošću. Dobijeni odgovori će biti odluka sistema.

Metoda razmaka

Ovo je najlakši način za rješavanje sistema nejednakosti, a istovremeno je univerzalan i rasprostranjen. Koristi se u srednjoj školi, pa čak iu srednjoj školi. Njegova suština je u tome da učenik traži intervale nejednakosti na brojevnoj pravoj, koja je ucrtana u svesku (ovo nije grafik, već obična ravna linija sa brojevima). Tamo gdje se seku intervali nejednačina, nalazi se rješenje sistema. Da biste koristili metodu razmaka, morate slijediti ove korake:

1. Svi članovi svake nejednakosti prenose se na lijevu stranu sa promjenom predznaka u suprotni (na desnoj je nula).
2. Nejednačine se ispisuju zasebno, a rješenje svake od njih se određuje.
3. Nalaze se presjeci nejednačina na realnoj pravoj. Svi brojevi na ovim raskrsnicama će biti rješenje.

Koji način koristiti?

Očigledno onaj koji se čini najlakšim i najprikladnijim, ali postoje slučajevi kada zadaci zahtijevaju određenu metodu. Najčešće kažu da morate riješiti ili pomoću grafa ili pomoću metode intervala. Algebarska metoda i supstitucija se koriste izuzetno rijetko ili se uopće ne koriste, jer su prilično složene i zbunjujuće, a osim toga, više se koriste za rješavanje sistema jednačina, a ne nejednačina, pa bi trebalo pribjeći crtanju grafova i intervala. Oni donose vidljivost, što ne može a da ne doprinese efikasnom i brzom izvođenju matematičkih operacija.

Ako nešto ne radi

Prilikom proučavanja određene teme iz algebre, naravno, mogu se pojaviti problemi s njenim razumijevanjem. I to je normalno, jer je naš mozak tako dizajniran da nije u stanju razumjeti složeni materijal u jednom potezu. Često morate ponovo pročitati pasus, uzeti pomoć nastavnika ili vježbati rješavanje tipičnih problema. U našem slučaju izgledaju, na primjer, ovako: "Riješi sistem nejednačina 3 x + 1 ≥ 0 i 2 x - 1 > 3". Dakle, lična nastojanja, pomoć trećih strana i praksa pomažu u razumijevanju bilo koje složene teme.

Reshebnik?

I knjiga rješenja je također vrlo prikladna, ali ne za varanje domaće zadaće, već za samopomoć. U njima možete pronaći sisteme nejednakosti s rješenjem, pogledati ih (kao obrasce), pokušati shvatiti kako se točno autor rješenja nosio sa zadatkom, a zatim pokušati to učiniti sami.

zaključci

Algebra je jedan od najtežih predmeta u školi. Pa, šta ti možeš? Matematika je oduvijek bila ovakva: nekima je lako, a drugima je teško. Ali u svakom slučaju, treba imati na umu da je opći obrazovni program osmišljen tako da se svaki učenik može nositi s njim. Osim toga, morate imati na umu ogroman broj asistenata. Neki od njih su gore pomenuti.

Program za rješavanje linearnih, kvadratnih i frakcionih nejednačina ne daje samo odgovor na problem, već daje detaljno rješenje sa objašnjenjima, tj. prikazuje proces rješavanja u cilju provjere znanja iz matematike i/ili algebre.

Štaviše, ako je u procesu rješavanja jedne od nejednakosti potrebno riješiti npr. kvadratna jednačina, zatim je prikazano i njegovo detaljno rješenje (uključeno je u spojler).

Ovaj program može biti koristan srednjoškolcima u pripremi za kontrolni rad, roditelji da kontrolišu rješavanje nejednakosti od strane svoje djece.

Ovaj program može biti od koristi srednjoškolcima u pripremi za testove i ispite, prilikom provjere znanja prije Jedinstvenog državnog ispita, roditeljima za kontrolu rješavanja mnogih zadataka iz matematike i algebre. Ili vam je možda preskupo unajmiti nastavnika ili kupiti nove udžbenike? Ili samo želite da to završite što je prije moguće? zadaća matematika ili algebra? U tom slučaju možete koristiti i naše programe sa detaljnim rješenjem.

Na taj način možete sami provoditi obuku i/ili obuku vaše mlađe braće ili sestara, dok se nivo obrazovanja u oblasti zadataka koji se rješavaju povećava.

Pravila za unos nejednakosti

Bilo koje latinično slovo može djelovati kao varijabla.
Na primjer: \(x, y, z, a, b, c, o, p, q \) itd.

Brojevi se mogu unositi kao cijeli brojevi ili razlomci.
Štaviše, razlomci brojeva može se uneti ne samo kao decimalni, već i kao običan razlomak.

Pravila za unos decimalnih razlomaka.
U decimalnim razlomcima, razlomački dio od cijelog broja može se odvojiti tačkom ili zarezom.
Na primjer, možete unijeti decimale ovako: 2,5x - 3,5x^2

Pravila za unos običnih razlomaka.
Samo cijeli broj može biti brojnik, nazivnik i cijeli broj razlomka.

Imenilac ne može biti negativan.

Prilikom unosa brojčanog razlomka, brojilac je odvojen od nazivnika znakom dijeljenja: /
Cjelobrojni dio je odvojen od razlomka ampersandom: &
Ulaz: 3&1/3 - 5&6/5y +1/7y^2
Rezultat: \(3\frac(1)(3) - 5\frac(6)(5) y + \frac(1)(7)y^2 \)

Zagrade se mogu koristiti prilikom unosa izraza. U ovom slučaju, prilikom rješavanja nejednakosti, izrazi se prvo pojednostavljuju.
Na primjer: 5(a+1)^2+2&3/5+a > 0,6(a-2)(a+3)

Odaberite željeni znak nejednakosti i unesite polinome u polja ispod.

Prva nejednakost sistema.

Kliknite na dugme za promjenu tipa prve nejednakosti.

> >= < <=

Riješite sistem nejednačina

Utvrđeno je da neke skripte potrebne za rješavanje ovog zadatka nisu učitane i program možda neće raditi.
Možda imate omogućen AdBlock.
U tom slučaju, onemogućite ga i osvježite stranicu.

U vašem pretraživaču je onemogućen JavaScript.
JavaScript mora biti omogućen da bi se rješenje pojavilo.
Evo instrukcija kako da omogućite JavaScript u vašem pretraživaču.

Jer Ima puno ljudi koji žele riješiti problem, vaš zahtjev je u redu.
Nakon nekoliko sekundi, rješenje će se pojaviti ispod.
Sačekaj molim te sec...

Ako ti uočio grešku u rješenju, onda o tome možete pisati u Obrascu za povratne informacije.
Nemoj zaboraviti naznačiti koji zadatak ti odluči šta unesite u polja.

Naše igre, zagonetke, emulatori:

Malo teorije.

Sistemi nejednakosti sa jednom nepoznatom. Numerički rasponi

U 7. razredu ste se upoznali sa pojmom sistema i naučili da rešavate sisteme linearnih jednačina sa dve nepoznate. Zatim će se razmatrati sistemi linearnih nejednačina sa jednom nepoznatom. Skupovi rješenja sistema nejednačina mogu se napisati korištenjem intervala (intervali, poluintervali, segmenti, zraci). Također ćete naučiti o zapisu numeričkih intervala.

Ako je u nejednačinama \(4x > 2000 \) i \(5x \leq 4000 \) nepoznati broj x isti, tada se ove nejednakosti razmatraju zajedno i kaže se da čine sistem nejednačina: $$ \left\ (\begin( array)(l) 4x > 2000 \\ 5x \leq 4000 \end(array)\right.$$

Vitičasta zagrada pokazuje da trebate pronaći takve vrijednosti x za koje se obje nejednakosti sistema pretvaraju u prave numeričke nejednakosti. Ovaj sistem- primjer sistema linearnih nejednakosti sa jednom nepoznatom.

Rješenje sistema nejednačina sa jednom nepoznatom je vrijednost nepoznate pri kojoj se sve nejednakosti sistema pretvaraju u prave numeričke nejednakosti. Riješiti sistem nejednačina znači pronaći sva rješenja ovog sistema ili utvrditi da ih nema.

Nejednačine \(x \geq -2 \) i \(x \leq 3 \) mogu se zapisati kao dvostruka nejednakost: \(-2 \leq x \leq 3 \).

Rješenja sistema nejednačina sa jednom nepoznatom su razna setovi brojeva. Ovi setovi imaju imena. Dakle, na realnoj osi, skup brojeva x takvih da je \(-2 \leq x \leq 3 \) predstavljen segmentom sa krajevima u tačkama -2 i 3.

-2

3

Ako je \(a segment i označen je sa [a; b]

Ako je \(interval i označen sa (a; b)

Skupovi brojeva \(x \) koji zadovoljavaju nejednakosti \(a \leq x po poluintervalima i označeni su sa [a; b) i (a; b] respektivno

Zovu se segmenti, intervali, poluintervali i zraci numeričke intervale.

Dakle, numerički intervali se mogu specificirati u obliku nejednačina.

Rješenje nejednakosti s dvije nepoznanice je par brojeva (x; y) koji ovu nejednakost pretvara u pravu numeričku nejednakost. Riješiti nejednakost znači pronaći skup svih njenih rješenja. Dakle, rješenja nejednakosti x > y bit će, na primjer, parovi brojeva (5; 3), (-1; -1), budući da \(5 \geq 3 \) i \(-1 \geq - 1\)

Rješavanje sistema nejednačina

Već ste naučili kako riješiti linearne nejednačine s jednom nepoznatom. Znati šta su sistem nejednakosti i rješenje sistema. Stoga vam proces rješavanja sistema nejednakosti sa jednom nepoznatom neće stvarati poteškoće.

Pa ipak, podsjećamo: da biste riješili sistem nejednačina, morate riješiti svaku nejednakost posebno, a zatim pronaći sjecište ovih rješenja.

Na primjer, prvobitni sistem nejednakosti je sveden na oblik:
$$ \left\(\begin(array)(l) x \geq -2 \\ x \leq 3 \end(array)\right. $$

Da biste riješili ovaj sistem nejednačina, označite rješenje svake nejednačine na realnoj osi i pronađite njihov presjek:

-2

3

Raskrsnica je segment [-2; 3] - ovo je rješenje originalnog sistema nejednačina.

U ovom članku odgovaram na još jedno pitanje mojih pretplatnika. Pitanja su drugačija. Nisu svi ispravno formulisani. A neki od njih su tako formulisani da nije moguće odmah shvatiti šta autor želi da pita. Stoga, među ogromnom količinom poslanih pitanja, moram izdvojiti zaista zanimljive, takve „bisere“, čiji su odgovori ne samo uzbudljivi, već i korisni, kako mi se čini, za moje ostale čitaoce. Danas odgovaram na jedno od tih pitanja. Kako predstaviti skup rješenja sistema nejednačina?


Zaista je dobro pitanje. Zato što je metoda grafičkog rješavanja problema u matematici vrlo moćna metoda. Osoba je raspoređena na takav način da mu je prikladnije da percipira informacije uz pomoć različitih vizualnih materijala. Stoga, ako savladate ovu metodu, vjerujte mi, ona će vam biti neophodna i pri rješavanju zadataka iz Jedinstvenog državnog ispita, posebno iz drugog dijela, drugih ispita, i pri rješavanju zadataka optimizacije i tako dalje i tako dalje.

Dakle. Kako možemo odgovoriti na ovo pitanje? Počnimo jednostavno. Neka sistem nejednačina sadrži samo jednu varijablu .

Primjer 1. Nacrtajte skup rješenja sistema nejednačina: Title="(!LANG:Rendered by QuickLaTeX.com">!}

Hajde da pojednostavimo ovaj sistem. Da bismo to učinili, oba dijela prve nejednakosti dodamo 7 i oba dijela podijelimo sa 2, bez promjene predznaka nejednakosti, jer je 2 pozitivan broj. Oba dijela druge nejednakosti dodajemo 4. Kao rezultat, dobivamo sledeći sistem nejednakosti:

Title="(!LANG:Rendered by QuickLaTeX.com">!}

Obično se takav problem naziva jednodimenzionalnim. Zašto? Da, jer da bi se prikazao skup njegovih rješenja dovoljna je ravna linija. Tačnije brojevna prava. Obratite pažnju na tačke 6 i 8 na ovoj brojevnoj pravoj. Jasno je da će tačka 8 biti desno od tačke 6, jer na brojevnoj pravoj veliki brojevi nalaze se desno od manjih. Osim toga, tačka 8 će biti zasjenjena, jer je prema zapisu prve nejednakosti uključena u njeno rješenje. Naprotiv, tačka 6 će biti neobojena, jer nije uključena u rješenje druge nejednačine:

Označimo sada strelicom iznad vrijednosti koje su manje ili jednake 8, kako zahtijeva prva nejednakost sistema, a strelicom odozdo vrijednosti koje su veće od 6, kako se zahtijeva po drugoj nejednakosti sistema:

Ostaje da se odgovori na pitanje gdje se na brojevnoj pravoj nalaze rješenja sistema nejednačina. Zapamtite jednom za svagda. Znak sistema - vitičasta zagrada - u matematici zamjenjuje uniju "I". Odnosno, prevodeći jezik formula na ljudski jezik, možemo reći da smo dužni navesti vrijednosti koje su veće od 6 I manje od ili jednake 8. To jest, traženi interval leži na raskrižju od označenih intervala:

Dakle, skup rješenja sistema nejednačina smo prikazali na realnoj pravoj ako sistem nejednačina sadrži samo jednu varijablu. Ovaj zasjenjeni interval uključuje sve vrijednosti za koje su zadovoljene sve nejednakosti zapisane u sistemu.

Razmotrite sada više težak slučaj. Neka naš sistem sadrži nejednakosti s dvije varijable i . U ovom slučaju neće biti moguće upravljati samo ravnom linijom koja bi predstavljala rješenja takvog sistema. Idemo dalje od jednodimenzionalnog svijeta i dodajemo mu drugu dimenziju. Ovdje nam treba cijeli avion. Razmotrite situaciju na konkretnom primjeru.

Dakle, kako se može opisati skup rješenja datog sistema nejednačina sa dvije varijable u pravokutnom koordinatnom sistemu na ravni? Počnimo s najjednostavnijim. Zapitajmo se koja je površina ove ravni definisana nejednakošću. Jednačina definira pravu liniju koja prolazi okomito na osu OX kroz tačku (0;0). To jest, u stvari, ova linija se poklapa sa osom OY. Pa, pošto nas zanimaju vrijednosti koje su veće ili jednake 0, onda će cijela poluravnina koja leži desno od prave linije učiniti:

Štaviše, sve tačke koje leže na osi OY, nam takođe odgovaraju, jer nejednakost nije stroga.

Da biste razumjeli koje područje na koordinatnoj ravni definira treću nejednakost, trebate nacrtati funkciju. Ovo je prava linija koja prolazi kroz ishodište i, na primjer, tačku (1;1). To je, u stvari, prava linija koja sadrži simetralu ugla koji čini prvu koordinatnu četvrtinu.

Pogledajmo sada treću nejednakost u sistemu i razmislimo o tome. Koje područje treba da pronađemo? Da vidimo: . Znak veće ili jednako. Odnosno, situacija je slična onoj u prethodnom primjeru. Samo ovdje „više“ ne znači „više udesno“, već „više“. jer OY Ovo je naša vertikalna os. To jest, površina definisana na ravni trećom nejednakošću je skup tačaka iznad ili na pravoj:

Sa prvom nejednakošću sistema, to je nešto manje zgodno. Ali kada smo bili u mogućnosti da definiramo opseg treće nejednakosti, mislim da je jasno kako dalje.

Ovu nejednakost je potrebno prikazati na način da je samo varijabla lijevo, a samo varijabla desno. Da bismo to učinili, oduzimamo nejednakost s obje strane i dijelimo obje strane sa 2 bez promjene predznaka nejednakosti, jer je 2 pozitivan broj. Kao rezultat, dobijamo sljedeću nejednakost:

Ostaje samo nacrtati na koordinatnoj ravni ravnu liniju koja siječe os OY u tački A(0;4) i prava linija u tački . Ovo poslednje sam naučio tako što sam izjednačio prave delove jednačina pravih i dobio jednačinu. Iz ove jednačine se nalazi koordinata tačke preseka, a koordinata je, mislim da ste pogodili, jednaka koordinati. Za one koji još uvijek nisu pogodili, to je zato što imamo jednadžbu jedne od linija koje se sijeku:.

Čim povučemo ovu pravu liniju, možemo odmah označiti područje koje tražimo. Znak nejednakosti ovdje je „manji ili jednak“. To znači da se željeno područje nalazi ispod ili direktno na prikazanoj liniji:

Pa, poslednje pitanje. Gdje je, uostalom, željena regija koja zadovoljava sve tri nejednakosti sistema? Očigledno se nalazi na raskrsnici sva tri označena područja. Opet prelaz! Zapamtite: znak sistema u matematici znači presek. Evo ga, ovo područje:

Pa, posljednji primjer. Još opštije. Pretpostavimo sada da u sistemu imamo ne jednu varijablu i ne dvije, već čak tri!

Pošto postoje tri varijable, da bismo predstavili skup rješenja takvog sistema nejednakosti, potrebna nam je treća dimenzija pored dvije s kojima smo radili u prethodnom primjeru. Odnosno, izlazimo iz ravni u svemir i već prikazujemo prostorni koordinatni sistem sa tri dimenzije: X, Y i Z. Što odgovara dužini, širini i visini.

Počnimo tako što ćemo u ovom koordinatnom sistemu prikazati površinu datu jednadžbom. Po obliku je vrlo sličan jednadžbi kružnice na ravni, samo se dodaje još jedan član sa promjenljivom. Lako je pretpostaviti da je ovo jednačina sfere sa centrom u tački (1; 3; 2), čiji je kvadrat poluprečnika 4. To jest, sam poluprečnik je 2.

Onda pitanje. I šta onda postavlja samu nejednakost? Za one koji su zbunjeni ovim pitanjem, predlažem da rezonuju na sljedeći način. Prevodeći jezik formula na ljudski, možemo reći da je potrebno naznačiti sve sfere sa centrom u tački (1;3;2), čiji su poluprečniki manji ili jednaki 2. Ali tada će sve te sfere biti unutar prikazana sfera! To jest, u stvari, ova nejednakost definira cjelinu unutrašnja regija prikazanu sferu. Ako želite, daje se lopta, ograničena prikazanom sferom:

Površina data jednadžbom x+y+z=4 je ravan koja seče koordinatne ose u tačkama (0;0;4), (0;4;0) i (4;0;0). Pa, jasno je da što je veći broj desno od znaka jednakosti, to će tačke presjeka ove ravni sa koordinatnim osama biti dalje od centra koordinata. Odnosno, druga nejednakost definira poluprostor koji se nalazi "iznad" date ravni. Koristeći uslovni izraz "više", mislim dalje u smjeru povećanja vrijednosti koordinata duž osi.

Ova ravan seče prikazanu sferu. U ovom slučaju, poprečni presjek je krug. Možete čak izračunati koliko je centar ovog kruga udaljen od centra koordinatnog sistema. Inače, ko pogodi kako se ovo radi neka svoja rješenja i odgovore napiše u komentarima. Dakle, originalni sistem nejednakosti definiše oblast prostora koja je dalje od ove ravni u pravcu rastućih koordinata, ali je zatvorena u prikazanoj sferi:

Ovako je prikazan skup rješenja sistema nejednačina. Ako u sistemu postoji više od 3 varijable (na primjer, 4), više neće biti moguće vizualno prikazati skup rješenja. Zato što bi za to bio potreban 4-dimenzionalni koordinatni sistem. Ali normalna osoba nije u stanju da zamisli kako bi se mogle locirati 4 međusobno okomite koordinatne ose. Mada imam prijatelja koji tvrdi da to može, i to sa lakoćom. Ne znam da li govori istinu, možda istinu. Ipak, normalna ljudska mašta to ne dozvoljava.

Nadam se da vam je današnja lekcija bila korisna. Da provjerite koliko ste dobro naučili, uradite domaći zadatak u nastavku.

Nacrtaj skup rješenja sistema nejednačina:

ql-right-eqno"> title="(!LANG:Rendered by QuickLaTeX.com">!}

Priredio Sergej Valerijevič

Lekcija i prezentacija na temu: "Sistemi nejednakosti. Primjeri rješenja"

Dodatni materijali
Dragi korisnici, ne zaboravite ostaviti svoje komentare, povratne informacije, sugestije! Svi materijali su provjereni antivirusnim programom.

Nastavna sredstva i simulatori u internet prodavnici "Integral" za 9. razred
Interaktivni vodič za učenje za 9. razred "Pravila i vježbe iz geometrije"
Elektronski udžbenik "Razumljiva geometrija" za 7-9 razred

Sistem nejednakosti

Ljudi, učili ste linearno i kvadratne nejednakosti naučili kako riješiti probleme na ove teme. Sada pređimo na novi koncept u matematici - sistem nejednakosti. Sistem nejednačina je sličan sistemu jednačina. Sjećate li se sistema jednačina? Učili ste sisteme jednačina u sedmom razredu, pokušajte se sjetiti kako ste ih rješavali.

Hajde da uvedemo definiciju sistema nejednakosti.
Nekoliko nejednakosti sa nekom promenljivom x formiraju sistem nejednakosti ako treba da pronađete sve vrednosti x za koje svaka od nejednačina čini pravi numerički izraz.

Bilo koja vrijednost x takva da svaka nejednakost daje valjani numerički izraz je rješenje nejednakosti. Može se nazvati i privatnom odlukom.
Šta je privatno rješenje? Na primjer, u odgovoru smo dobili izraz x>7. Tada je x=8, ili x=123, ili neki drugi broj veći od sedam posebno rješenje, a izraz x>7 je opšte rješenje. Opće rješenje je formirano skupom posebnih rješenja.

Kako smo kombinovali sistem jednačina? Tako je, vitičasta zagrada, tako da rade isto sa nejednakostima. Pogledajmo primjer sistema nejednakosti: $\begin(cases)x+7>5\\x-3
Ako se sistem nejednačina sastoji od identičnih izraza, na primjer, $\begin(cases)x+7>5\\x+7
Dakle, šta znači pronaći rješenje za sistem nejednakosti?
Rješenje nejednakosti je skup parcijalnih rješenja nejednakosti koji istovremeno zadovoljava obje nejednakosti sistema.

Opći oblik sistema nejednačina pišemo kao $\begin(cases)f(x)>0\\g(x)>0\end(cases)$

Neka je $X_1$ opšte rješenje nejednačine f(x)>0.
$X_2$ je opšte rješenje nejednačine g(x)>0.
$X_1$ i $X_2$ su skup konkretnih rješenja.
Rješenje sistema nejednačina će biti brojevi koji pripadaju i $X_1$ i $X_2$.
Pogledajmo operacije na skupovima. Kako možemo pronaći elemente skupa koji pripadaju oba skupa odjednom? Tako je, postoji operacija raskrsnice za ovo. Dakle, rješenje naše nejednakosti će biti skup $A= X_1∩ X_2$.

Primjeri rješenja sistema nejednačina

Pogledajmo primjere rješavanja sistema nejednačina.

Riješite sistem nejednačina.
a) $\begin(slučajevi)3x-1>2\\5x-10 b) $\begin(slučajevi)2x-4≤6\\-x-4
Rješenje.
a) Riješite svaku nejednačinu posebno.
$3x-1>2; \; 3x>3; \; x>1$.
$5x-10
Označavamo naše intervale na jednoj koordinatnoj liniji.

Rješenje sistema će biti segment sjecišta naših intervala. Nejednakost je stroga, tada će segment biti otvoren.
Odgovor: (1;3).

B) Također rješavamo svaku nejednačinu posebno.
$2x-4≤6; 2x≤ 10; x ≤ $5.
$-x-4 -5 $.


Rješenje sistema će biti segment sjecišta naših intervala. Druga nejednakost je stroga, tada će segment biti otvoren s lijeve strane.
Odgovor: (-5; 5).

Hajde da sumiramo šta smo naučili.
Pretpostavimo da trebamo riješiti sistem nejednakosti: $\begin(cases)f_1 (x)>f_2 (x)\\g_1 (x)>g_2 (x)\end(cases)$.
Tada je interval ($x_1; x_2$) rješenje prve nejednakosti.
Interval ($y_1; y_2$) je rješenje druge nejednačine.
Rješenje sistema nejednačina je presjek rješenja svake nejednačine.

Sistemi nejednakosti mogu se sastojati od nejednakosti ne samo prvog reda, već i bilo koje druge vrste nejednakosti.

Važna pravila za rješavanje sistema nejednačina.
Ako jedna od nejednakosti sistema nema rješenja, onda cijeli sistem nema rješenja.
Ako je jedna od nejednakosti zadovoljena za bilo koju vrijednost varijable, tada će rješenje sistema biti rješenje druge nejednakosti.

Primjeri.
Riješite sistem nejednačina:$\begin(cases)x^2-16>0\\x^2-8x+12≤0 \end(cases)$
Rješenje.
Riješimo svaku nejednačinu posebno.
$x^2-16>0$.
$(x-4)(x+4)>0$.

Rešimo drugu nejednačinu.
$x^2-8x+12≤0$.
$(x-6)(x-2)≤0$.

Rješenje nejednakosti je jaz.
Nacrtajmo oba intervala na jednoj pravoj liniji i nađemo raskrsnicu.
Presjek intervala je segment (4; 6).
Odgovor: (4;6).

Riješite sistem nejednačina.
a) $\begin(slučajevi)3x+3>6\\2x^2+4x+4 b) $\begin(slučajevi)3x+3>6\\2x^2+4x+4>0\end(slučajevi )$.

Rješenje.
a) Prva nejednačina ima rješenje x>1.
Nađimo diskriminant za drugu nejednakost.
$D=16-4 * 2 * 4=-16$. $D Prisjetite se pravila, kada jedna od nejednačina nema rješenja, onda cijeli sistem nema rješenja.
Odgovor: Ne postoje rješenja.

B) Prva nejednačina ima rješenje x>1.
Druga nejednakost je veća od nule za sve x. Tada se rješenje sistema poklapa sa rješenjem prve nejednačine.
Odgovor: x>1.

Zadaci o sistemima nejednačina za nezavisno rješenje

Riješite sisteme nejednačina:
a) $\begin(slučajevi)4x-5>11\\2x-12 b) $\begin(slučajevi)-3x+1>5\\3x-11 c) $\begin(slučajevi)x^2-25 d) $\begin(cases)x^2-16x+55>0\\x^2-17x+60≥0 \end(cases)$
e) $\begin(cases)x^2+36