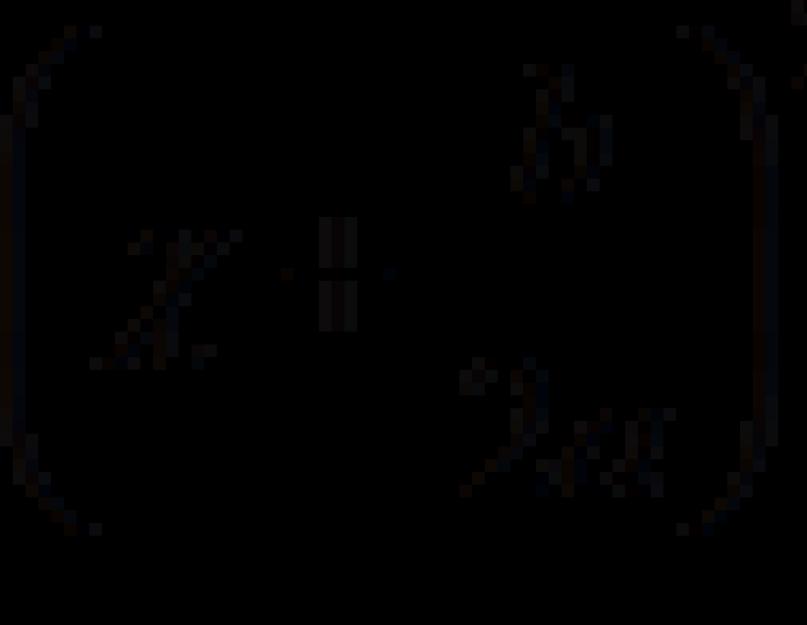Iz istorije nastanka kvadratne jednačine

Algebra je nastala u vezi s rješavanjem raznih problema korištenjem jednadžbi. Obično je u zadacima potrebno pronaći jednu ili više nepoznanica, uz poznavanje rezultata nekih radnji izvršenih na željenim i datim veličinama. Takvi se problemi svode na rješavanje jedne ili sistema od više jednačina, na pronalaženje željenih uz pomoć algebarskih operacija nad datim veličinama. Studije algebre opšta svojstva akcije na količine.

Neke algebarske tehnike za rješavanje linearnih i kvadratnih jednadžbi bile su poznate još prije 4000 godina u Drevni Babilon.

Kvadratne jednadžbe u starom Babilonu

Potreba za rješavanjem jednačina ne samo prvog, već i drugog stepena u antičko doba bila je uzrokovana potrebom rješavanja problema vezanih za pronalaženje površina kopna i zemljanih radova vojnog karaktera, kao i razvojem astronomije i sama matematika. Babilonci su znali kako riješiti kvadratne jednačine oko 2000. godine prije Krista. Primjenjujući modernu algebarsku notaciju, možemo reći da u njihovim klinastim tekstovima, osim nepotpunih, postoje i takve, na primjer, potpune kvadratne jednadžbe:

https://pandia.ru/text/78/002/images/image002_15.gif" width="93" height="41 src=">

Pravilo za rješavanje ovih jednačina, navedeno u vavilonskim tekstovima, u suštini se poklapa sa savremenim, ali nije poznato kako su Babilonci došli do ovog pravila. Gotovo svi do sada pronađeni klinasti tekstovi daju samo probleme s rješenjima navedenim u obliku recepata, bez naznake kako su pronađeni. Uprkos visoki nivo razvoj algebre u Babilonu, klinastim tekstovima nedostaje koncept negativan broj i uobičajene metode rješenja kvadratnih jednadžbi.

Diofantova aritmetika ne sadrži sistematsko izlaganje algebre, ali sadrži sistematski niz zadataka, praćenih objašnjenjima i rešavanih sastavljanjem jednačina različitih stepeni.

Prilikom sastavljanja jednačina, Diofant vješto bira nepoznanice kako bi pojednostavio rješenje.

Evo, na primjer, jednog od njegovih zadataka.

Zadatak 2. "Pronađi dva broja, znajući da je njihov zbir 20, a proizvod 96."

Diofant tvrdi kako slijedi: iz uvjeta zadatka slijedi da željeni brojevi nisu jednaki, jer da su jednaki, onda bi njihov proizvod bio jednak ne 96, već 100. Dakle, jedan od njih će biti veći od polovina njihovog zbira, tj. .10 + x. Drugi je manji, tj. 10 - x. Razlika između njih je 2x. Otuda jednačina:

(10+x)(10-x)=96,

Otuda je x = 2. Jedan od željenih brojeva je 12, drugi je 8. Rešenje x = - 2 za Diofanta ne postoji, pošto je grčka matematika poznavala samo pozitivne brojeve.

Ako riješimo ovaj problem, odabirom jednog od nepoznatih brojeva kao nepoznatog, možemo doći do rješenja jednadžbe:

Jasno je da Diofant pojednostavljuje rješenje birajući polurazliku željenih brojeva kao nepoznatu; on uspijeva svesti problem na rješavanje nepotpune kvadratne jednačine.

Kvadratne jednadžbe u Indiji

Problemi za kvadratne jednačine se već nalaze u astronomskoj raspravi Aryabhattam, koju je 499. godine sastavio indijski matematičar i astronom Aryabhatta. Drugi indijski učenjak, Brahmagupta (7. vek), je izložio opšte pravilo rješenja kvadratnih jednadžbi svedena na jedan kanonski oblik:

ax2 + bx = c, a>

U jednačini (1) koeficijenti mogu biti negativni. Brahmaguptino pravilo se u suštini poklapa s našim.

U Indiji su javna takmičenja u rješavanju teških problema bila uobičajena. U jednoj od starih indijskih knjiga o ovakvim takmičenjima se kaže: „Kao što sunce svojim sjajem obasjava zvezde, tako naučnik čovek pomračiti slavu u popularnim skupovima, nudeći i rješavajući algebarske probleme. Zadaci su često bili obučeni u poetsku formu.

Evo jednog od problema poznatog indijskog matematičara iz XII veka. Bhaskara.

Bhaskarino rješenje ukazuje da je autor bio svjestan dvovrijednosti korijena kvadratnih jednačina.

Jednačina koja odgovara problemu 3 je:

https://pandia.ru/text/78/002/images/image004_11.gif" width="12" height="26 src=">x2 - 64x = - 768

i dopuniti lijeva strana ove jednadžbe do kvadrata, dodaje 322 na obje strane, a zatim dobiva:

x2 - b4x + 322 = -768 + 1024,

(x - 32) 2 = 256,

x1 = 16, x2 = 48.

Al-Khwarizmijeve kvadratne jednadžbe

Al-Khwarizmijeva algebarska rasprava daje klasifikaciju linearnih i kvadratnih jednadžbi. Autor navodi 6 vrsta jednačina, izražavajući ih na sljedeći način:

1) „Kvadrati su jednaki korijenima“, tj. ax2 = bx.

2) „Kvadrati su jednaki broju“, tj. ax2 = c.

3) "Korijeni su jednaki broju", odnosno sjekira \u003d c.

4) “Kvadrati i brojevi su jednaki korijenima”, odnosno ax2 + c = bx.

5) „Kvadrati i korijeni su jednaki broju“, tj. ax2 + bx = c.

6) “Korijeni i brojevi su jednaki kvadratima”, tj. bx + c == ax2.

Za Al-Khwarizmija, koji je izbjegavao korištenje negativnih brojeva, članovi svake od ovih jednačina su sabirci, a ne oduzimanje. U ovom slučaju se očito ne uzimaju u obzir jednačine koje nemaju pozitivna rješenja. Autor iznosi metode za rješavanje ovih jednačina, koristeći metode al-jabr i al-muqabala. Njegova odluka se, naravno, ne poklapa u potpunosti s našom. Da ne spominjemo činjenicu da je riječ o čisto retorici, treba napomenuti, na primjer, da prilikom rješavanja nepotpune kvadratne jednačine prvog tipa, Al-Khwarizmi, kao i svi matematičari prije 17. stoljeća, ne uzima u obzir nulu rješenje, vjerovatno zato što u konkretnim praktičnim zadacima nije bitno. Kada rješava potpune kvadratne jednadžbe, Al-Khwarizmi postavlja pravila za njihovo rješavanje koristeći određene numeričke primjere, a zatim i njihove geometrijske dokaze.

Uzmimo primjer.

Zadatak 4. „Kvadrat i broj 21 jednaki su 10 korijena. Pronađite korijen ”(podrazumijeva se korijen jednadžbe x2 + 21 = 10x).

Rješenje: podijelite broj korijena na pola, dobijete 5, pomnožite 5 sa sobom, oduzmete 21 od proizvoda, ostane 4. Uzmite korijen od 4, dobijete 2. Oduzmite 2 od 5, dobijete 3, ovo će biti željeni korijen. Ili dodajte 2 do 5, što će dati 7, ovo je također korijen.

Al-Khwarizmijeva rasprava je prva knjiga koja je došla do nas, u kojoj je sistematski prikazana klasifikacija kvadratnih jednadžbi i date formule za njihovo rješavanje.

Kvadratne jednačine u EvropiXII- XVIIin.

Forme za rješavanje kvadratnih jednačina po modelu Al-Khwarizmija u Evropi su prvi put opisane u "Knjizi Abacusa", napisanoj 1202. godine. Italijanski matematičar Leonard Fibonacci. Autor je samostalno razvio neke nove algebarske primjere rješavanja problema i prvi u Europi pristupio uvođenju negativnih brojeva.

Ova knjiga je doprinijela širenju algebarskog znanja ne samo u Italiji, već iu Njemačkoj, Francuskoj i drugim evropskim zemljama. Mnogi zadaci iz ove knjige preneti su u skoro sve evropske udžbenike 14.-17. veka. Opće pravilo za rješavanje kvadratnih jednačina svedenih na jedan kanonski oblik x2 + bx = c sa svim mogućim kombinacijama predznaka i koeficijenata b, c, formulisao je u Evropi 1544. godine M. Stiefel.

Izvođenje formule za rješavanje kvadratne jednadžbe u opšti pogled Viet ima, ali Viet je prepoznao samo pozitivne korijene. Italijanski matematičari Tartaglia, Cardano, Bombelli bili su među prvima u 16. veku. uzeti u obzir, pored pozitivnih, i negativne korijene. Tek u XVII veku. zahvaljujući djelima Girarda, Descartesa, Newtona i drugih naučnim putem rješavanje kvadratnih jednačina poprima moderan oblik.

Poreklo algebarskih metoda za rešavanje praktičnih problema vezano je za nauku antički svijet. Kao što je poznato iz istorije matematike, značajan deo problema matematičke prirode, koje su rešavali egipatski, sumerski, vavilonski pisari-računari (XX-VI vek pre nove ere), imao je proračunsku prirodu. Međutim, i tada su se s vremena na vrijeme javljali problemi u kojima je željena vrijednost veličine određena nekim indirektnim uvjetima, koji su zahtijevali, sa naše moderne tačke gledišta, formulaciju jednačine ili sistema jednačina. U početku su se za rješavanje takvih problema koristile aritmetičke metode. Kasnije su se počeli formirati počeci algebarskih reprezentacija. Na primjer, babilonski kalkulatori su mogli riješiti probleme koji se mogu smanjiti u smislu moderna klasifikacija na jednačine drugog stepena. Stvorena je metoda za rješavanje tekstualnih zadataka, koja je kasnije poslužila kao osnova za isticanje algebarske komponente i njeno samostalno proučavanje.

Ovo istraživanje je već bilo provedeno u drugoj eri, prvo od strane arapskih matematičara (VI-X stoljeće nove ere), koji su izdvojili karakteristične radnje kojima su jednačine svedene na standardni pogled redukcija sličnih članova, prenošenje članova iz jednog dijela jednačine u drugi s promjenom predznaka. A onda su evropski matematičari renesanse, kao rezultat dugog traganja, stvorili jezik moderne algebre, upotrebu slova, uvođenje simbola za aritmetičke operacije, zagrade itd. Na prelazu iz 16. 17. vijeka. Algebra kao poseban dio matematike, koji ima svoj predmet, metodu, područja primjene, već je formirana. Njegov dalji razvoj, do našeg vremena, sastojao se u poboljšanju metoda, proširenju obima primjene, razjašnjavanju pojmova i njihovih veza sa pojmovima drugih grana matematike.

Dakle, s obzirom na važnost i prostranost materijala povezanog s konceptom jednačine, njegovo proučavanje u savremena metodologija matematika je povezana sa tri glavna područja njenog nastanka i funkcionisanja.

Da biste riješili bilo koju kvadratnu jednačinu, morate znati:

formula za pronalaženje diskriminanta;

formula za pronalaženje korijena kvadratne jednadžbe;

· Algoritmi za rješavanje jednačina ovog tipa.

rješavati nepotpune kvadratne jednadžbe;

riješiti potpune kvadratne jednadžbe;

riješiti date kvadratne jednačine;

pronaći greške u riješenim jednačinama i ispraviti ih;

Proveri.

Rješenje svake jednadžbe sastoji se od dva glavna dijela:

transformacija ove jednadžbe u najjednostavnije;

rješavanje jednačina prema poznata pravila, formule ili algoritme.

Generalizacija metoda aktivnosti učenika u rješavanju kvadratnih jednačina odvija se postepeno. Prilikom proučavanja teme "Kvadratne jednadžbe" mogu se razlikovati sljedeće faze:

Faza I - "Rješavanje nepotpunih kvadratnih jednadžbi."

Faza II - "Rješenje kompletnih kvadratnih jednadžbi."

Faza III - "Rješenje redukovane kvadratne jednadžbe."

U prvoj fazi razmatraju se nepotpune kvadratne jednadžbe. Pošto su u početku matematičari naučili rješavati nepotpune kvadratne jednadžbe, jer za to nisu morali ništa, kako kažu, izmišljati. Ovo su jednadžbe oblika: ax2 = 0, ax2 + c = 0, gdje je c≠ 0, ax2 + bx = 0, gdje je b ≠ 0. Razmotrimo rješenje nekoliko ovih jednačina:

1. Ako je ax2 = 0. Jednačine ovog tipa rješavaju se prema algoritmu:

1) naći x2;

2) naći x.

Na primjer, 5x2 = 0. Podijeleći obje strane jednačine sa 5, ispada: x2 = 0, dakle x = 0.

2. Ako je ax2 + c = 0, c≠ 0 Jednačine ovog tipa rješavaju se prema algoritmu:

1) pomeriti pojmove na desnu stranu;

2) pronaći sve brojeve čiji su kvadrati jednaki broju c.

Na primjer, x2 - 5 = 0, Ova jednadžba je ekvivalentna jednadžbi x2 = 5. Dakle, morate pronaći sve brojeve čiji su kvadrati jednaki broju 5..gif" width="16" height="19 ">..gif" width=" 16" height="19 src="> i nema drugih korijena.

3. Ako je ah2 + bh = 0, b ≠ 0. Jednačine ove vrste se rješavaju prema algoritmu:

1) pomeriti zajednički faktor iz zagrada;

2) naći x1, x2.

Na primjer, x2 - 3x = 0. Prepišimo jednačinu x2 - 3x = 0 u obliku x (x - 3) = 0. Ova jednadžba očito ima korijene x1 = 0, x2 = 3. nema drugih korijena, jer ako u zamjenu za bilo koji broj osim nule i 3 umjesto x, tada na lijevoj strani jednadžbe x (x - 3) = 0 dobivate broj koji nije jednak nuli.

Dakle, ovi primjeri pokazuju kako se rješavaju nepotpune kvadratne jednadžbe:

1) ako jednačina ima oblik ax2 = 0, tada ima jedan korijen x = 0;

2) ako jednačina ima oblik ax2 + bx = 0, tada se koristi metoda faktorizacije: x (ax + b) = 0; dakle ili x = 0 ili ax + b = 0..gif" width="16" height="41"> U slučaju -< 0, уравнение х2 = - не имеет корней (значит, не имеет корней и исходное уравнение ах2 + с = 0). В случае, когда - >0, tj. - = m, gdje je m>0, jednadžba x2 = m ima dva korijena

https://pandia.ru/text/78/002/images/image010_9.gif" width="29" height="24 src=">.gif" width="29" height="24 src=">, (u ovom slučaju je dozvoljena kraća oznaka =.

Dakle, nepotpuna kvadratna jednadžba može imati dva korijena, jedan korijen, bez korijena.

U drugoj fazi se vrši prijelaz na rješenje potpune kvadratne jednadžbe. To su jednadžbe oblika ax2 + bx + c = 0, gdje su a, b, c dati brojevi, a ≠ 0, x je nepoznata.

Svaka potpuna kvadratna jednadžba se može pretvoriti u oblik , kako bi se odredio broj korijena kvadratne jednadžbe i pronašao te korijene. Razmatraju se sljedeći slučajevi rješavanja potpunih kvadratnih jednačina: D< 0, D = 0, D > 0.

1. Ako D< 0, то квадратное уравнение ах2 + bx + c = 0 не имеет действительных корней.

Na primjer, 2x2 + 4x + 7 = 0. Rješenje: ovdje je a = 2, b = 4, c = 7.

D \u003d b2 - 4ac \u003d 42 - 4 * 2 * 7 \u003d 16 - 56 \u003d - 40.

Od D< 0, то данное квадратное уравнение не имеет корней.

2. Ako je D = 0, tada kvadratna jednadžba ax2 + bx + c = 0 ima jedan korijen, koji se nalazi po formuli.

Na primjer, 4x - 20x + 25 = 0. Rješenje: a = 4, b = - 20, c = 25.

D \u003d b2 - 4ac = (-20) 2 - 4 * 4 * 25 = 400 - 400 \u003d 0.

Pošto je D = 0, ova jednadžba ima jedan korijen. Ovaj korijen se nalazi pomoću formule ..gif" width="100" height="45">.gif" width="445" height="45 src=">.

Sastavljen je algoritam za rješavanje jednadžbe oblika ax2 + bx + c = 0.

1. Izračunajte diskriminanta D koristeći formulu D = b2 - 4ac.

2. Ako D< 0, то квадратное уравнение ах2 + bx + c = 0 не имеет корней.

3. Ako je D = 0, tada kvadratna jednadžba ima jedan korijen, koji se nalazi po formuli

4..gif" width="101" height="45">.

Ovaj algoritam je univerzalan, primjenjiv je i na nepotpune i na potpune kvadratne jednadžbe. Međutim, nepotpune kvadratne jednadžbe se obično ne rješavaju ovim algoritmom.

Matematičari su praktični, ekonomični ljudi, pa koriste formulu: https://pandia.ru/text/78/002/images/image022_5.gif" width="155" height="53">. (4)

2..gif" width="96" height="49 src="> ima isti predznak kao D..gif" width="89" height="49"> tada jednadžba (3) ima dva korijena;

2) ako tada jednačina ima dva podudarna korijena;

3) ako tada jednačina nema korijena.

Važna tačka u proučavanju kvadratnih jednadžbi je razmatranje Vietine teoreme, koja navodi postojanje veze između korena i koeficijenata redukovane kvadratne jednačine.

Vietin teorem. Zbir korijena date kvadratne jednadžbe jednak je drugom koeficijentu, uzetom iz suprotan znak, a proizvod korijena jednak je slobodnom članu.

Drugim riječima, ako su x1 i x2 korijeni jednadžbe x2 + px + q = 0, tada

Ove formule se zovu Vietine formule u čast francuskog matematičara F. Viete (), koji je uveo sistem algebarskih simbola, razvio osnove elementarne algebre. Bio je jedan od prvih koji je brojeve počeo označavati slovima, što je značajno razvilo teoriju jednadžbi.

Na primjer, gornja jednadžba x2 - 7x +10 \u003d 0 ima korijene 2 i 5. Zbir korijena je 7, a proizvod je 10. Može se vidjeti da je zbroj korijena jednak drugom koeficijentu , uzet sa suprotnim predznakom, a proizvod korijena jednak je slobodnom članu.

Postoji i teorema suprotna Vietinoj teoremi.

Teorema inverzna Vietinoj teoremi. Ako formule (5) vrijede za brojeve x1, x2, p, q, tada su x1 i x2 korijeni jednadžbe x2 + px + q = 0.

Vietina teorema i njena inverzna teorema se često koriste u rješavanju različitih problema.

Na primjer. Napišimo datu kvadratnu jednačinu čiji su korijeni brojevi 1 i -3.

Prema Vietinim formulama

– p = x1 + x2 = - 2,

Prema tome, željena jednačina ima oblik x2 + 2x - 3 = 0.

Složenost savladavanja Vietine teoreme povezana je s nekoliko okolnosti. Prije svega, potrebno je uzeti u obzir razliku između direktnih i inverznih teorema. U Vietinoj direktnoj teoremi, date su kvadratna jednadžba i njeni korijeni; u inverzu postoje samo dva broja, a kvadratna jednadžba se pojavljuje na kraju teoreme. Učenici često griješe potkrepljujući svoje razmišljanje netačnim pozivanjem na direktnu ili inverznu Vietinu teoremu.

Na primjer, kada se odabirom pronalaze korijeni kvadratne jednadžbe, morate se pozvati na inverznu Vietinu teoremu, a ne na direktnu, kao što studenti često rade. Da bismo proširili Vietine teoreme na slučaj nulte diskriminante, moramo se složiti da u ovom slučaju kvadratna jednadžba ima dva jednaka korijena. Pogodnost takvog dogovora očituje se u faktorizaciji kvadratnog trinoma.

Istraživački rad

Na temu

"Metode za rješavanje kvadratnih jednačina"

Izvedeno:
grupa 8 "G" razred

Rukovodilac posla:
Benkovskaya Maria Mikhailovna

Ciljevi i zadaci projekta.

1. Pokažite da matematika, kao i svaka druga nauka, ima dovoljno svojih neriješenih misterija.
2. Naglasite da se matematičari razlikuju po nestandardnom razmišljanju. A ponekad i duhovitost i intuicija dobar matematicar jednostavno su neverovatne!
3. Pokazati da je sam pokušaj rješavanja kvadratnih jednačina doprinio razvoju novih pojmova i ideja u matematici.
4. Naučite raditi s različitim izvorima informacija.
5. Nastaviti istraživački rad iz matematike

Faze istraživanja

1. Istorija nastanka kvadratnih jednačina.

2. Definicija kvadratne jednadžbe i njeni tipovi.

3. Rješavanje kvadratnih jednadžbi pomoću diskriminantne formule.

4. Francois Viet i njegova teorema.

5. Svojstva koeficijenata za brzo pronalaženje korijena kvadratne jednadžbe.

6. Praktična orijentacija.

Kroz jednačine, teoreme

Rešio sam dosta problema.

(Chaucer, engleski pesnik, srednje godine.)

pozornici. Istorija nastanka kvadratnih jednačina.

Potreba za rješavanjem jednačina ne samo prvog, već i drugog stepena, još u antici bila je uzrokovana potrebom rješavanja problema vezanih za pronalaženje područja zemljišne parcele i zemljanih radova vojnog karaktera, kao i razvojem same astronomije i matematike.

Babilonci su bili u stanju da reše kvadratne jednačine oko 2000. godine pre nove ere. Pravilo za rješavanje ovih jednačina, navedeno u babilonskim tekstovima, u suštini se poklapa sa modernim, ali nije poznato kako su Babilonci došli do pravila. Gotovo svi do sada pronađeni klinasti tekstovi daju samo probleme s rješenjima navedenim u obliku recepata, bez naznake kako su pronađeni.

Uprkos visokom nivou razvoja algebre u Babilonu, klinastim tekstovima nedostaje koncept negativnog broja i opšte metode za rešavanje kvadratnih jednačina.

Diofantova "Aritmetika" sadrži sistematski niz problema, praćenih objašnjenjima i rješavanih formuliranjem jednačina raznih stepeni, ali mu nedostaje sistematsko izlaganje algebre.

Problemi za kvadratne jednačine se već nalaze u astronomskim raspravama "Aryabhattiam", sastavljenim 499. godine. Indijski matematičar i astronom Aryabhatta. Drugi indijski naučnik, Brahmagupta (7. vek), izložio je opšte pravilo za rešavanje kvadratnih jednačina svedenih na jedan kanonski oblik:

Al-Khorezmijeva algebarska rasprava daje klasifikaciju linearnih i kvadratnih jednadžbi. Autor ima 6 vrsta jednačina. Za al-Khwarizmija, koji nije znao negativne brojeve, članovi svake jednačine su zbrajanja, a ne oduzimanja. Istovremeno, jednadžbe koje nemaju pozitivna rješenja se namjerno ne uzimaju u obzir; pri rješavanju nepotpune kvadratne jednačine, al-Khwarizmi, kao i svi naučnici prije 17. stoljeća, ne uzima u obzir nulto rješenje.

Traktat al-Khwarizmi je prva knjiga koja je došla do nas, u kojoj je sistematski prikazana klasifikacija kvadratnih jednadžbi i formule za njihovo rješavanje.

Formule za rješavanje kvadratnih jednačina po modelu al-Khwarizmija u Evropi su prvi put izložene u Knjizi Abacusa koju je 1202. godine napisao italijanski matematičar Leonardo Fibonacci. Ovaj obimni rad odlikuje se potpunošću i jasnoćom prezentacije. Autor je samostalno razvio neke nove algebarske metode za rješavanje problema, te je prvi u Europi pristupio uvođenju negativnih brojeva. Njegova knjiga je doprinijela širenju algebarskog znanja ne samo u Italiji, već iu Njemačkoj, Francuskoj i drugim evropskim zemljama. Mnogi problemi iz Knjige Abakusa prešli su u gotovo sve evropske udžbenike 16.-17. i djelimično 18. vijeka.

Opće pravilo za rješavanje kvadratnih jednadžbi svedeno na jedan kanonski oblik sa svim mogućim kombinacijama znakova koeficijenti b,c je u Evropi formulisao M. Stiefel tek 1544. godine.

Vieta ima opći izvod formule za rješavanje kvadratne jednadžbe, ali Vieta je prepoznao samo pozitivne korijene. Italijanski matematičari Tartaglia, Cardano, Bombelli među prvima su u 16. veku uzeli u obzir ne samo pozitivne, već i negativne korene. Tek u 17. vijeku, zahvaljujući radovima Girrarda, Descartesa, Newtona i drugih naučnika, metoda rješavanja kvadratnih jednačina dobija moderan oblik.

ISPADA:

Zadaci o kvadratnim jednačinama nalaze se već u 499.

AT drevna Indija podijeljena su javna takmičenja u rješavanju teških zadataka – OLIMPIJADE .

©2015-2019 stranica
Sva prava pripadaju njihovim autorima. Ova stranica ne tvrdi autorstvo, ali omogućava besplatno korištenje.
Datum kreiranja stranice: 2016-04-11

UVOD

Jednačine u školskom kursu algebre vodeće mjesto. Više vremena posvećeno je njihovom proučavanju nego bilo kojoj drugoj temi školskog kursa matematike. Snaga teorije jednadžbi je u tome što ona nema samo teorijski značaj za poznavanje prirodnih zakona, već služi i u specifične praktične svrhe. Najviše problema o prostornim oblicima i kvantitativnim odnosima stvarnom svijetu svodi se na odluku razne vrste jednačine. Savladavajući načine njihovog rješavanja, ljudi pronalaze odgovore razna pitanja iz nauke i tehnologije (saobraćaj, Poljoprivreda, industrija, komunikacije, itd.). Takođe, za formiranje sposobnosti rješavanja jednačina od velikog je značaja i samostalan rad učenika u učenju rješavanja jednačina. Prilikom proučavanja bilo koje teme, jednačine se mogu koristiti kao efikasno sredstvo za konsolidaciju, produbljivanje, ponavljanje i proširenje teorijskih znanja, za razvoj kreativne matematičke aktivnosti učenika.

U savremenom svetu jednačine se široko koriste u različitim granama matematike, u rešavanju važnih primenjenih problema. Ovu temu karakteriše velika dubina izlaganja i bogatstvo veza uspostavljenih uz pomoć u učenju, logička valjanost izlaganja. Stoga zauzima izuzetan položaj u nizu jednačina. Studenti počinju proučavati temu „Kvadratni trinomi“ nakon što su već stekli određeno iskustvo, posjedujući prilično veliku zalihu algebarskih i općih matematičkih koncepata, koncepata i vještina. U velikoj mjeri, upravo na materijalu ove teme potrebno je sintetizirati gradivo vezano za jednačine, implementirati principe historizma i pristupačnosti.

Relevantnost Tema je potreba implementacije principa istoricizma i nedostatak materijala za implementaciju ovoga na temu "Rješenje kvadratnih jednačina".

Problem istraživanja: identificiranje povijesnog materijala za učenje rješavanja kvadratnih jednačina.

Cilj: formiranje ideja o radu na kvadratnim jednadžbama na časovima matematike, izbor seta lekcija sa elementima historizma na temu "Kvadrične jednadžbe".

Predmet proučavanja: rješavanje kvadratnih jednadžbi u 8. razredu korištenjem elemenata historicizma.

Predmet studija: kvadratne jednadžbe i izrada lekcija o učenju rješavanja kvadratnih jednadžbi koristeći historijsku građu.

Zadaci:

vrši analizu naučne i metodološke literature o problemu istraživanja;

analizirati školske udžbenike i istaći u njima mjesto učenja rješavanja kvadratnih jednačina;

pokupiti set lekcija o rješavanju kvadratnih jednačina koristeći povijesne materijale.

Metode istraživanja:

analiza literature na temu "Rješenje kvadratnih jednadžbi";

posmatranje učenika tokom časa na temu "Rješavanje kvadratnih jednačina";

izbor materijala: lekcije na temu "Rješavanje kvadratnih jednadžbi" koristeći povijesnu referencu.

§ 1. Iz istorije nastanka kvadratnih jednačina

Algebra je nastala u vezi s rješavanjem raznih problema korištenjem jednadžbi. Obično je u zadacima potrebno pronaći jednu ili više nepoznanica, uz poznavanje rezultata nekih radnji izvršenih na željenim i datim veličinama. Takvi se problemi svode na rješavanje jedne ili sistema od više jednačina, na pronalaženje željenih uz pomoć algebarskih operacija nad datim veličinama. Algebra proučava opšta svojstva akcija na veličine.

Neke algebarske tehnike za rješavanje linearnih i kvadratnih jednačina bile su poznate još prije 4000 godina u starom Babilonu.

Kvadratne jednadžbe u starom Babilonu

Pravilo za rješavanje ovih jednačina, navedeno u vavilonskim tekstovima, u suštini se poklapa sa savremenim, ali nije poznato kako su Babilonci došli do ovog pravila. Gotovo svi do sada pronađeni klinasti tekstovi daju samo probleme s rješenjima navedenim u obliku recepata, bez naznake kako su pronađeni. Uprkos visokom nivou razvoja algebre u Babilonu, klinastim tekstovima nedostaje koncept negativnog broja i opšte metode za rešavanje kvadratnih jednačina.

Diofantova aritmetika ne sadrži sistematsko izlaganje algebre, ali sadrži sistematski niz zadataka, praćenih objašnjenjima i rešavanih sastavljanjem jednačina različitih stepeni.

Prilikom sastavljanja jednačina, Diofant vješto bira nepoznanice kako bi pojednostavio rješenje.

Evo, na primjer, jednog od njegovih zadataka.

Zadatak 2. "Pronađi dva broja, znajući da je njihov zbir 20, a proizvod 96."

Diofant tvrdi kako slijedi: iz uvjeta zadatka slijedi da željeni brojevi nisu jednaki, jer da su jednaki, onda bi njihov proizvod bio jednak ne 96, već 100. Dakle, jedan od njih će biti veći od polovina njihove sume, tj.
. Drugi je manji, tj.
. Razlika između njih
. Otuda jednačina:

Odavde
. Jedan od željenih brojeva je 12, drugi je 8. Rješenje
jer Diofant ne postoji, pošto je grčka matematika poznavala samo pozitivne brojeve.

Ako riješimo ovaj problem, odabirom jednog od nepoznatih brojeva kao nepoznatog, možemo doći do rješenja jednadžbe:

Jasno je da Diofant pojednostavljuje rješenje birajući polurazliku željenih brojeva kao nepoznatu; on uspijeva svesti problem na rješavanje nepotpune kvadratne jednačine.

Kvadratne jednadžbe u Indiji

Problemi za kvadratne jednačine se već nalaze u astronomskoj raspravi Aryabhattam, koju je 499. godine sastavio indijski matematičar i astronom Aryabhatta. Drugi indijski naučnik, Brahmagupta (7. vek), izložio je opšte pravilo za rešavanje kvadratnih jednačina svedenih na jedan kanonski oblik:

(1)

U jednačini (1) koeficijenti mogu biti negativni. Brahmaguptino pravilo se u suštini poklapa s našim.

U Indiji su javna takmičenja u rješavanju teških problema bila uobičajena. U jednoj od starih indijskih knjiga o takvim takmičenjima kaže se sljedeće: „Kao što sunce obasjava zvijezde svojim sjajem, tako će učena osoba zasjeniti slavu na javnim skupovima, predlažući i rješavajući algebarske probleme.“ Zadaci su često bili obučeni u poetsku formu.

Evo jednog od problema poznatog indijskog matematičara iz XII veka. Bhaskara.

Bhaskarino rješenje ukazuje da je autor bio svjestan dvovrijednosti korijena kvadratnih jednačina.

Jednačina koja odgovara problemu 3 je:

Bhaskara piše pod maskom:

i, da bi dopunio lijevu stranu ove jednadžbe na kvadrat, dodaje 322 na obje strane, dobivajući tada:

Al-Khwarizmijeve kvadratne jednadžbe

Al-Khwarizmijeva algebarska rasprava daje klasifikaciju linearnih i kvadratnih jednadžbi. Autor navodi 6 vrsta jednačina, izražavajući ih na sljedeći način:

Uzmimo primjer.

Zadatak 4. „Kvadrat i broj 21 jednaki su 10 korijena. Pronađite korijen" (što znači korijen jednadžbe
).

Al-Khwarizmijeva rasprava je prva knjiga koja je došla do nas, u kojoj je sistematski prikazana klasifikacija kvadratnih jednadžbi i date formule za njihovo rješavanje.

Kvadratne jednačine u EvropiXII- XVIIin.

Ova knjiga je doprinijela širenju algebarskog znanja ne samo u Italiji, već iu Njemačkoj, Francuskoj i drugim evropskim zemljama. Mnogi zadaci iz ove knjige preneti su u skoro sve evropske udžbenike 14.-17. veka. Opće pravilo za rješavanje kvadratnih jednadžbi svedeno na jedan kanonski oblik
sa svim mogućim kombinacijama znakova i koeficijenata b, c, formulirao je u Evropi 1544. godine M. Stiefel.

Vieta ima opći izvod formule za rješavanje kvadratne jednadžbe, ali Vieta je prepoznao samo pozitivne korijene. Italijanski matematičari Tartaglia, Cardano, Bombelli bili su među prvima u 16. veku. uzeti u obzir, pored pozitivnih, i negativne korijene. Tek u XVII veku. zahvaljujući radovima Girarda, Descartesa, Newtona i drugih naučnika, metoda rješavanja kvadratnih jednačina poprima moderan oblik.

Poreklo algebarskih metoda za rešavanje praktičnih problema povezano je sa naukom antičkog sveta. Kao što je poznato iz istorije matematike, značajan deo problema matematičke prirode, koje su rešavali egipatski, sumerski, vavilonski pisari-računari (XX-VI vek pre nove ere), imao je proračunsku prirodu. Međutim, i tada su se s vremena na vrijeme javljali problemi u kojima je željena vrijednost veličine određena nekim indirektnim uvjetima, koji su zahtijevali, sa naše moderne tačke gledišta, formulaciju jednačine ili sistema jednačina. U početku su se za rješavanje takvih problema koristile aritmetičke metode. Kasnije su se počeli formirati počeci algebarskih reprezentacija. Na primjer, babilonski kalkulatori su mogli riješiti probleme koji se, sa stanovišta moderne klasifikacije, svode na jednačine drugog stepena. Stvorena je metoda za rješavanje tekstualnih zadataka, koja je kasnije poslužila kao osnova za isticanje algebarske komponente i njeno samostalno proučavanje.

Ovu studiju su već izveli u neko drugo doba, prvo od strane arapskih matematičara (VI-X stoljeće nove ere), koji su izdvojili karakteristične radnje kojima se jednačine svode na standardni oblik, redukciju sličnih članova, prijenos pojmova iz jednog dijela jednačina na drugu sa promjenom predznaka. A onda su evropski matematičari renesanse, kao rezultat dugog traganja, stvorili jezik moderne algebre, upotrebu slova, uvođenje simbola za aritmetičke operacije, zagrade itd. Na prelazu iz 16. 17. vijeka. Algebra kao poseban dio matematike, koji ima svoj predmet, metodu, područja primjene, već je formirana. Njegov dalji razvoj, do našeg vremena, sastojao se u poboljšanju metoda, proširenju obima primjene, razjašnjavanju pojmova i njihovih veza sa pojmovima drugih grana matematike.

Dakle, s obzirom na važnost i obimnost materijala koji je povezan sa konceptom jednačine, njeno proučavanje u savremenoj metodologiji matematike povezano je sa tri glavna područja njenog nastanka i funkcionisanja.

Početna > Prijavi

MOU srednja škola nazvana po herojima Sovjetski savez
Sotnikova A.T. i Shepeleva N. G. s. Uritskoe

Izvještaj na temu:

„Istorija nastanka

kvadratne jednadžbe"

Pripremljen od:Izotova Julia,
Ampleeva Elena,
Šepelev Nikolaj,

Dyachenko Yuri.

Oh matematika. Vekovima si prekriven slavom,

Svetiljka svih zemaljskih svetiljki.

Ti veličanstvena kraljice

Nije ni čudo što je Gauss kršten.

Strog, logičan, veličanstven,

Vitka u letu, kao strijela,

Tvoja večna slava

Kroz vekove je stekla besmrtnost.

Hvalimo ljudski um

njegova djela magične ruke,

Nada ovog doba

Kraljica svih zemaljskih nauka.

Želimo vam reći danas

Istorija pojave

Šta svaki učenik treba da zna

Istorija kvadratnih jednačina.

Euklid, u III veku pre nove ere. e. u svojim "Načelima" posvetio je geometrijskoj algebri cijelu drugu knjigu, koja sadrži sav potreban materijal za rješavanje kvadratnih jednačina.

Euklid (Eνκλειδηζ), starogrčki matematičar, autor prve teorijske rasprave o matematici koja je došla do nas

Podaci o Euklidu su izuzetno oskudni. Jedina stvar koja se može smatrati pouzdanom je to naučna djelatnost tekla u Aleksandriji u III veku pre nove ere. e. Euklid je prvi matematičar Aleksandrijske škole. Njegovo glavni posao"Počeci" (u latiniziranom obliku - "Elementi") sadrži prikaz planimetrije, stereometrije i niz pitanja iz teorije brojeva; u njemu je sažeo prethodni razvoj grčke matematike i stvorio temelj dalji razvoj matematike. Heron - Grčki matematičar i inženjer po prvi put u Grčkoj u 1. veku nove ere. daje čisto algebarski način rješavanja kvadratne jednačine.

Heron od Aleksandrije; Čaplja, I c. n. e., grčki mehaničar i matematičar. Vrijeme njegovog života je neizvjesno, poznato je samo da je citirao Arhimeda (koji je umro 212. pne), njega samog citira Papus (oko 300. godine nove ere). Trenutno preovlađuje mišljenje da je živio u 1. vijeku. n. e. Studirao je geometriju, mehaniku, hidrostatiku, optiku; izumio prototip parne mašine i precizne instrumente za nivelisanje. Najpopularniji automati bili su automatska pozorišta, fontane i dr. G. je opisao teodolit, oslanjajući se na zakone statike i kinetike, i dao opis poluge, bloka, propelera i vojnih vozila. U optici je formulirao zakone refleksije svjetlosti, u matematici - metode za mjerenje najvažnijih geometrijski oblici. Glavna G.-ova djela su Etrika, Pneumatika, Autopoetika, Mehanika (francuski; djelo je u potpunosti sačuvano na arapskom), Katoptika (nauka o ogledalima; sačuvana samo u Latinski prijevod) i dr. G. je koristio dostignuća svojih prethodnika: Euklida, Arhimeda, Stratona iz Lampsaka. Njegov stil je jednostavan i jasan, iako ponekad previše lakonski ili nestrukturiran. Interesovanje za spise G. pojavilo se u III veku. n. e. Grčki, a potom i vizantijski i arapski studenti komentirali su i prevodili njegova djela.

Diofant- grčki naučnik je u 3. veku nove ere, ne pribegavajući geometriji, rešio neke kvadratne jednačine na čisto algebarski način, a sama jednačina i njeno rešenje su zapisani u simboličkom obliku

“Reći ću vam kako je grčki matematičar Diofant sastavio i riješio kvadratne jednačine. Evo, na primjer, jednog od njegovih zadataka:"Pronađi dva broja znajući da je njihov zbir 20, a proizvod 96."

1. Iz uslova zadatka proizilazi da željeni brojevi nisu jednaki, jer da su jednaki, onda njihov proizvod ne bi bio 96, već 100.

2. Dakle. jedan od njih će biti više od polovine njihove sume, tj. 10 + x, drugi je manji, tj. 10 - x.

3. Razlika između njih je 2x.

4. Otuda jednačina (10 + x) * (10 - x) = 96

100 - x 2 = 96 x 2 - 4 = 0

5. Odgovor x = 2. Jedan od željenih brojeva je 12,
ostalo - 8. Rješenje x = - 2 za Diofanta ne postoji, jer Grčka matematika je znala samo pozitivne brojeve.” Diofant je znao riješiti vrlo složene jednačine, korištene za nepoznato slovne oznake, uveo je poseban simbol za izračunavanje, koristio skraćenice riječi. Bhaskare - Akaria- Indijski matematičar u XII veku nove ere. otkrio opću metodu za rješavanje kvadratnih jednačina.

Analizirajmo jedan od problema indijskih matematičara, na primjer, problem Bhaskare:

“Jato majmuna se zabavlja: osmina od ukupnog broja njih na kvadratu se brčka u šumi, preostalih dvanaest vrište na vrhu humka. Reci mi koliko ima majmuna?"

Komentarišući problem, želio bih reći da jednačina (x/8) 2 + 12 = x odgovara problemu. Bhaskara piše kao x 2 - 64x \u003d - 768. Dodavanjem kvadrata 32 na oba dijela, jednadžba će dobiti oblik:

x 2 - 64 x + 32 2 = - 768 + 1024

(x - 32) 2 = 256

Nakon izvlačenja kvadratnog korijena, dobijamo: x - 32 = 16.

„AT ovaj slučaj, kaže Bhaskara, - negativne jedinice prvog dijela su takve da su jedinice drugog dijela manje od njih, pa se potonji mogu smatrati i pozitivnim i negativnim, i dobijamo dvostruku vrijednost nepoznate: 48 i 16.

Mora se zaključiti da Bhaskarino rješenje ukazuje da je znao za dvovrijednost korijena kvadratnih jednačina.

Predlaže se rješavanje starog indijskog Bhaskara problema:

„Kvadrat petine majmuna, smanjen za tri, sakrio se u pećini, jedan majmun se popeo na drvo, bio je vidljiv. Koliko je majmuna bilo? Treba napomenuti da se ovaj problem rješava elementarno, svodeći se na kvadratnu jednačinu.

Al - Khorezmi - arapski učenjak koji je 825. godine napisao knjigu "Knjiga obnove i opozicije". Bio je to prvi udžbenik algebre na svijetu. Dao je i šest vrsta kvadratnih jednačina i za svaku od šest jednačina u verbalnom obliku formulisao posebno pravilo za njeno rješavanje. U raspravi, Horezmi navodi 6 vrsta jednačina, izražavajući ih na sljedeći način:

1. "Kvadrati su jednaki korijenima", tj. sjekira 2 = in.

2. "Kvadrati su jednaki broju", tj. ax 2 = s.

3. "Korijeni su jednaki broju", tj. ah = s.

4. "Kvadrati i brojevi su jednaki korijenima", tj. sjekira 2 + c \u003d in.

5. "Kvadrati i korijeni su jednaki broju", tj. ax 2 + in = s.

6. "Korijeni i brojevi su jednaki kvadratima", tj. u + c \u003d ah 2.

Analizirajmo problem al-Khwarizmija, koji se svodi na rješavanje kvadratne jednadžbe. "Kvadrat i broj jednaki su korijenima." Na primjer, jedan kvadrat i broj 21 jednaki su 10 korijena istog kvadrata, tj. postavlja se pitanje od čega se formira kvadrat koji, nakon što mu se doda 21, postaje jednak sa 10 korijena istog kvadrata?

I koristeći 4. formulu al-Khwarizmija, učenici moraju zapisati: x 2 + 21 = 10x

François Viet - Francuski matematičar, formulisao je i dokazao teoremu o zbiru i proizvodu korena date kvadratne jednačine.

Umjetnost koju predstavljam je nova, ili je barem toliko iskvarena utjecajem varvara da sam smatrao prikladnim da joj dam potpuno novi izgled.

François Viet

Ipak, François (1540-13.12. 1603) rođen je u gradu Fontenay-le-Comte u provinciji Poitou, nedaleko od čuvene tvrđave La Rochelle. Nakon što je stekao diplomu pravnika, od svoje devetnaeste godine uspješno se bavio advokaturom u rodnom gradu. Kao advokat, Viet je uživao ugled i poštovanje među stanovništvom. Bio je široko obrazovana osoba. Znao astronomiju i matematiku i sve ostalo slobodno vrijeme dao ovim naukama.

Glavna strast Vieta je bila matematika. Duboko je proučavao djela klasika Arhimeda i Diofanta, neposrednih prethodnika Cardana, Bombellija, Stevina i drugih. Vieta im se ne samo divio, već je u njima vidio veliku manu, a to je bilo teško razumijevanje zbog verbalne simbolike: Gotovo sve radnje i znakovi su zabilježeni riječima, nije bilo ni nagoveštaja onih zgodnih, gotovo automatskih pravila koja sada koristimo . Bilo je nemoguće zapisati i, prema tome, započeti u opštem obliku, algebarska poređenja ili bilo koje druge algebarske izraze. Svaka vrsta jednadžbe sa numeričkim koeficijentima rješavana je prema posebnom pravilu. Stoga je bilo potrebno dokazati da postoje opšte akcije nad svim brojevima koji ne zavise od samih ovih brojeva. Viet i njegovi sljedbenici su ustanovili da nije bitno da li je broj u pitanju broj objekata ili dužina segmenta. Glavna stvar je da je moguće izvoditi algebarske operacije s ovim brojevima i, kao rezultat, opet dobiti brojeve iste vrste. Stoga se mogu označiti nekim apstraktnim znakovima. Viet je upravo to uradio. On ne samo da je uveo svoj doslovni račun, već je napravio fundamentalno novo otkriće, postavljajući sebi cilj da proučava ne brojeve, već radnje na njima. Ovakav način pisanja omogućio je Vieti da napravi važna otkrića u proučavanju opštih svojstava algebarskih jednačina. Nije slučajno što Vieta nazivaju "ocem" algebre, osnivačem slovnih simbola.

Informativni resursi:

http :// som. fio. en/ resurse/ Karpuhina/2003/12/ Završeno%20 rad/ Koncert/ index1. htm

http :// stranice. marsu. en/ iac/ škola/ s4/ stranica74. html

Ministarstvo obrazovanja Ruske Federacije

Opštinska obrazovna ustanova

"Srednja škola №22"

Kvadratne jednačine i jednačine višeg reda

Završeno:

Učenici 8 "B" razreda

Kuznjecov Evgenij i Rudi Aleksej

Supervizor:

Zenina Alevtina Dmitrievna

nastavnik matematike

Uvod

1.1 Jednačine u starom Babilonu

1.2 Jednačine Arapa

1.3 Jednačine u Indiji

Poglavlje 2. Teorija kvadratnih jednačina i jednačina višeg reda

2.1 Osnovni koncepti

2.2 Formule parnih koeficijenata za x

2.3 Vietina teorema

2.4 Kvadratne jednačine posebne prirode

2.5 Vietina teorema za polinome (jednačine) viših stupnjeva

2.6 Jednačine koje se svode na kvadrate (bikvadratne)

2.7 Proučavanje bikvadratnih jednačina

2.8 Cordano formule

2.9 Simetrične jednačine trećeg stepena

2.10 Povratne jednačine

2.11 Hornerova šema

Zaključak

Bibliografija

Prilog 1

Aneks 2

Aneks 3

Uvod

Jednačine u školskom kursu algebre zauzimaju vodeće mjesto. Za učenje im je potrebno više vremena od bilo koje druge teme. Zaista, jednačine nemaju samo važan teorijski značaj, već služe i u čisto praktične svrhe. Ogromna većina problema o prostornim oblicima i kvantitativnim odnosima stvarnog svijeta svodi se na rješavanje različitih vrsta jednačina. Savladavajući načine njihovog rješavanja, nalazimo odgovore na razna pitanja iz nauke i tehnologije (saobraćaj, poljoprivreda, industrija, komunikacije itd.).

U ovom eseju želio bih prikazati formule i metode za rješavanje različitih jednačina. Za to su date jednačine koje se ne izučavaju u školskom programu. U osnovi, to su jednačine posebne prirode i jednačine viših stupnjeva. Da bismo otkrili ovu temu, dati su dokazi ovih formula.

Ciljevi našeg sažetka:

Poboljšajte vještine rješavanja jednačina

Razviti nove načine rješavanja jednačina

Naučite neke nove načine i formule za rješavanje ovih jednadžbi.

Predmet proučavanja je elementarna algebra, a predmet proučavanja jednačina. Izbor ove teme zasnivao se na činjenici da jednačine postoje i u osnovnom programu i u svakom narednom času. opšteobrazovne škole, liceji, fakulteti. Mnogi geometrijski problemi, problemi iz fizike, hemije i biologije rješavaju se pomoću jednačina. Jednačine su riješene prije dvadeset pet stoljeća. Izrađuju se i danas - oba za upotrebu u obrazovni proces, te za takmičarske ispite na univerzitetima, za olimpijade najvišeg nivoa.

Poglavlje 1. Istorija kvadratnih jednačina i jednačina višeg reda

1.1 Jednačine u starom Babilonu

Algebra je nastala u vezi s rješavanjem raznih problema korištenjem jednadžbi. Obično je u zadacima potrebno pronaći jednu ili više nepoznanica, uz poznavanje rezultata nekih radnji izvršenih na željenim i datim veličinama. Takvi se problemi svode na rješavanje jedne ili sistema od više jednačina, na pronalaženje željenih uz pomoć algebarskih operacija nad datim veličinama. Algebra proučava opšta svojstva akcija na veličine.

Neke algebarske tehnike za rješavanje linearnih i kvadratnih jednačina bile su poznate još prije 4000 godina u starom Babilonu. Potreba za rješavanjem jednačina ne samo prvog, već i drugog stepena u antičko doba bila je uzrokovana potrebom rješavanja problema vezanih za pronalaženje površina zemljišta i zemljišnih radova vojnog karaktera, kao i razvojem astronomije. i sama matematika. Kao što je ranije spomenuto, Babilonci su znali riješiti kvadratne jednačine oko 2000. godine prije Krista. Koristeći modernu algebarsku notaciju, može se reći da se u njihovim klinastim tekstovima pojavljuju i nepotpune i potpune kvadratne jednadžbe.

Pravilo za rješavanje ovih jednačina, navedeno u vavilonskim tekstovima, u suštini se poklapa sa modernim, ali nije poznato kako su Babilonci došli do ovog pravila. Gotovo svi do sada pronađeni klinasti tekstovi daju samo probleme s rješenjima navedenim u obliku recepata, bez naznake kako su pronađeni.

Uprkos visokom nivou razvoja algebre u Babilonu, u klinastim tekstovima ne postoji koncept negativnog broja i opšte metode za rešavanje kvadratne jednačine.

1.2 Jednačine Arapa

Neke metode za rješavanje jednačina, kako kvadratnih tako i jednačina viših stupnjeva, izveli su Arapi. Tako je poznati arapski matematičar Al-Khwarizmi u svojoj knjizi "Al-Jabar" opisao mnoge načine rješavanja različitih jednačina. Njihova posebnost je bila da je Al-Khwarizmi koristio kompleksne radikale da pronađe korijene (rješenja) jednačina. Potreba za rješavanjem ovakvih jednačina bila je potrebna u pitanjima o diobi nasljedstva.

1.3 Jednačine u Indiji

Kvadratne jednačine su također rješavane u Indiji. Problemi o kvadratnim jednačinama već se nalaze u astronomskoj raspravi Aryabhattam, koju je 499. godine sastavio indijski matematičar i astronom Aryabhatta. Drugi indijski učenjak, Brahmagupta (7. vek), izložio je opšte pravilo za rešavanje kvadratnih jednačina svedenih na jedan konusni oblik:

ax² + bx= c, gdje je a > 0

U ovoj jednačini koeficijenti, osim za a, mogu biti i negativni. Brahmaguptino pravilo se u suštini poklapa s našim.

U staroj Indiji javna takmičenja u rješavanju teških problema bila su uobičajena. Jedna od starih indijskih knjiga o takvim takmičenjima kaže sljedeće: „Kao što sunce sjaji zvijezde svojim sjajem, tako će učena osoba zasjeniti slavu drugoga na javnim skupovima, predlažući i rješavajući algebarske probleme“. Zadaci su često bili obučeni u poetsku formu.

Različite jednačine, kako kvadratne, tako i jednačine viših stupnjeva, rješavali su naši daleki preci. Ove jednačine su rješavane u najrazličitijim i međusobno udaljenim zemljama. Potreba za jednačinama je bila velika. Jednačine su se koristile u građevinarstvu, u vojnim poslovima iu svakodnevnim situacijama.

Poglavlje 2. Kvadratne jednačine i jednačine višeg reda

2.1 Osnovni koncepti

Kvadratna jednačina je jednačina oblika

gdje su koeficijenti a, b, c bilo koji realni brojevi, a a ≠ 0.

Kvadratna jednačina se naziva redukovanom ako je njen vodeći koeficijent 1.

Primjer :

x2 + 2x + 6 = 0.

Kvadratna jednadžba se naziva nesvedenom ako je vodeći koeficijent različit od 1.

Primjer :

2x2 + 8x + 3 = 0.

Potpuna kvadratna jednadžba je kvadratna jednačina u kojoj su prisutna sva tri člana, drugim riječima, ovo je jednačina u kojoj su koeficijenti b i c različiti od nule.

Primjer :

3x2 + 4x + 2 = 0.

Nepotpuna kvadratna jednadžba je kvadratna jednačina u kojoj je barem jedan koeficijent b, c jednak nuli.

Dakle, postoje tri vrste nepotpunih kvadratnih jednadžbi:

1) ax² = 0 (ima dva identična korijena x = 0).

2) ax² + bx = 0 (ima dva korijena x 1 = 0 i x 2 = -)

Primjer :

x 1 = 0, x 2 = -5.

Odgovori: x 1 = 0, x 2 = -5.

ako -<0 - уравнение не имеет корней.

Primjer :

Odgovori: jednačina nema korijena.

Ako je –> 0, tada je x 1,2 = ±

Primjer :

Odgovori: x 1,2 =±

Bilo koja kvadratna jednačina se može riješiti preko diskriminanta (b² - 4ac). Obično se izraz b² - 4ac označava slovom D i naziva se diskriminanta kvadratne jednačine ax² + bx + c = 0 (ili diskriminanta kvadrata tri člana ax² + bx + c)

Primjer :

x 2 +14x - 23 = 0

D \u003d b 2 - 4ac \u003d 144 + 92 \u003d 256

x 2 =

Odgovori: x 1 = 1, x 2 = - 15.

U zavisnosti od diskriminanta, jednačina može imati ili ne mora imati rješenje.

1) Ako D< 0, то не имеет решения.

2) Ako je D = 0, onda jednačina ima dva podudarna rješenja x 1,2 =

3) Ako je D > 0, onda ima dva rješenja, koja se nalaze po formuli:

x 1,2 =

2.2 Formule parnih koeficijenata za x

Navikli smo na činjenicu da su korijeni kvadratne jednadžbe

ax² + bx + c = 0 nalaze se po formuli

x 1,2 =

Ali matematičari nikada neće propustiti priliku da olakšaju svoje proračune. Otkrili su da se ova formula može pojednostaviti kada je koeficijent b oblika b = 2k, posebno ako je b paran broj.

Zaista, neka kvadratna jednačina ax² + bx + c = 0 ima koeficijent b oblika b = 2k. Zamjenom broja 2k umjesto b u našu formulu, dobijamo:

Dakle, korijeni kvadratne jednadžbe ax² + 2kx + c = 0 mogu se izračunati po formuli:

x 1,2 =

Primjer :

5x 2 - 2x + 1 = 0

Prednost ove formule je u tome što se od ovog kvadrata ne stavlja broj b, nego se od tog kvadrata oduzima njegova polovina, ne 4ac, već jednostavno ac, i, konačno, što nazivnik ne sadrži 2a, već jednostavno a.

Ako je data kvadratna jednadžba, onda će naša formula izgledati ovako:

Primjer :

x 2 - 4x + 3 = 0

Odgovori: x 1 = 3, x 2 = 1.

2.3 Vietina teorema

Vrlo zanimljivo svojstvo korijena kvadratne jednadžbe otkrio je francuski matematičar Francois Viet. Ovo svojstvo se zove Vietina teorema:

Tako da su brojevi x 1 i x 2 korijeni jednadžbe:

ax² + bx + c = 0

neophodno je i dovoljno da jednakost

x 1 + x 2 = -b/a i x 1 x 2 = c/a

Vietin teorem vam omogućava da procenite predznake i apsolutnu vrednost kvadratne jednačine

x² + bx + c = 0

1. Ako je b>0, c>0 tada su oba korijena negativna.

2. Ako b<0, c>0, tada su oba korijena pozitivna.

3. Ako je b>0, c<0 то уравнение имеет корни разных знаков, причём отрицательный корень по абсолютной величине больше положительного.

4. Ako b<0, c<0 то уравнение имеет корни разных знаков, причём отрицательный корень по абсолютной величине меньше положительного.

2.4 Kvadratne jednačine posebne prirode

1) Ako je a + b + c = 0 u jednačini ax² + bx + c = 0, tada

x 1 = 1 i x 2 =.

Dokaz :

U jednačini ax² + bx + c = 0, njeni korijeni

x 1,2 = (1).

Predstavimo b iz jednakosti a + b + c = 0

Ovaj izraz zamjenjujemo u formulu (1):

Ako odvojeno razmotrimo dva korijena jednadžbe, dobićemo:

1) x 1 =

2) x 2 =

Iz ovoga slijedi: x 1 = 1 i x 2 =.

1. Primjer :

2x² - 3x + 1 = 0

a=2, b=-3, c=1.

a + b + c = 0, dakle

2. Primjer :

418x² - 1254x + 836 = 0

Ovaj primjer je vrlo teško riješiti preko diskriminanta, ali znajući gornju formulu, lako se može riješiti.

a=418, b=-1254, c=836.

x 1 = 1 x 2 = 2

2) Ako je a - b + c = 0, u jednačini ax² + bx + c = 0, tada:

x 1 = -1 i x 2 = -.

Dokaz :

Razmotrimo jednačinu ax² + bx + c = 0, što implicira da:

x 1,2 = (2).

Predstavimo b iz jednakosti a - b + c = 0

b = a + c, zamijenimo u formulu (2):

Dobijamo dva izraza:

1) x 1 =

2) x 2 =

Ova formula je slična prethodnoj, ali je takođe važna, jer. često postoje primjeri ove vrste.

1) Primjer :

2x² + 3x + 1 = 0

a = 2, b = 3, c = 1.

a - b + c = 0, dakle

2)Primjer :

Odgovori: x 1 \u003d -1; x 2 = -

3) Metoda “ transferi ”

Korijeni kvadratnih jednadžbi y² + by + ac = 0 i ax² + bx + c = 0 povezani su relacijama:

x 1 = i x 2 =

Dokaz :

a) Razmotrimo jednačinu ax² + bx + c = 0

x 1,2 = =

b) Razmotrimo jednačinu y² + by + ac = 0

y 1,2 =

Imajte na umu da su diskriminanti oba rješenja jednaki, uporedimo korijene ove dvije jednačine. Međusobno se razlikuju po vodećim koeficijentom, korijeni prve jednadžbe su manji od korijena druge za a. Koristeći Vietinu teoremu i gornje pravilo, nije teško riješiti različite jednadžbe.

Primjer :

Imamo proizvoljnu kvadratnu jednačinu

10x² - 11x + 3 = 0

Ovu jednačinu transformiramo prema gore navedenom pravilu

y² - 11y + 30 = 0

Dobijamo redukovanu kvadratnu jednačinu, koja se lako može riješiti korištenjem Vietine teoreme.

Neka su y 1 i y 2 korijeni jednadžbe y² - 11y + 30 = 0

y 1 y 2 = 30 y 1 = 6

y 1 + y 2 = 11 y 2 = 5

Znajući da se korijeni ovih jednadžbi razlikuju jedan od drugog za a, onda

x 1 = 6/10 = 0,6

x 2 = 5/10 = 0,5

U nekim slučajevima, zgodno je prvo riješiti ne zadatu jednačinu ax² + bx + c = 0, već redukovanu y² + by + ac = 0, koja se dobija iz datog koeficijenta "transfera" a, a zatim podijeliti pronađeni korijene po a da se pronađe originalna jednačina.

2.5 Vieta formula za polinome (jednačine) viših stupnjeva

Formule koje je Vieta izveo za kvadratne jednačine važe i za polinome viših stupnjeva.

Neka je polinom

P(x) = a 0 x n + a 1 x n -1 + … +a n

Ima n različitih korijena x 1 , x 2 …, x n .

U ovom slučaju ima faktorizaciju oblika:

a 0 x n + a 1 x n-1 +…+ a n = a 0 (x – x 1)(x – x 2)…(x – x n)

Podijelimo oba dijela ove jednakosti sa 0 ≠ 0 i proširimo zagrade u prvom dijelu. Dobijamo jednakost:

x n + ()x n -1 + ... + () = x n - (x 1 + x 2 + ... + x n) x n -1 + (x 1 x 2 + x 2 x 3 + ... + x n) -1 x n)x n - 2 + … +(-1) n x 1 x 2 … x n

Ali dva polinoma su identično jednaka ako i samo ako su koeficijenti na istim stepenima jednaki. Iz ovoga slijedi da je jednakost

x 1 + x 2 + … + x n = -

x 1 x 2 + x 2 x 3 + … + x n -1 x n =

x 1 x 2 … x n = (-1) n

Na primjer, za polinome trećeg stepena

a 0 x³ + a 1 x² + a 2 x + a 3

Imamo identitete

x 1 + x 2 + x 3 = -

x 1 x 2 + x 1 x 3 + x 2 x 3 =

x 1 x 2 x 3 = -

Što se tiče kvadratnih jednadžbi, ova formula se zove Vieta formule. Lijevi dijelovi ovih formula su simetrični polinomi iz korijena x 1 , x 2 ..., x n date jednačine, a desni dijelovi su izraženi kroz koeficijent polinoma.

2.6 Jednačine koje se svode na kvadrate (bikvadratne)

Jednačine četvrtog stepena svode se na kvadratne jednačine:

ax 4 + bx 2 + c = 0,

naziva se bikvadratičnim, štaviše, a ≠ 0.

Dovoljno je staviti x 2 \u003d y u ovu jednačinu, dakle,

ay² + by + c = 0

pronaći korijene rezultirajuće kvadratne jednadžbe

y 1,2 =

Da biste odmah pronašli korijene x 1, x 2, x 3, x 4, zamijenite y sa x i dobijete

x2 =

x 1,2,3,4 = .

Ako jednadžba četvrtog stepena ima x 1, tada ima i korijen x 2 \u003d -x 1,

Ako ima x 3, onda je x 4 \u003d - x 3. Zbir korijena takve jednadžbe je nula.

Primjer :

2x 4 - 9x² + 4 = 0

Zamjenjujemo jednačinu u formulu za korijene bikvadratnih jednadžbi:

x 1,2,3,4 = ,

znajući da je x 1 = -x 2, i x 3 = -x 4, tada:

x 3,4 =

Odgovori: x 1,2 = ±2; x 1,2 =

2.7 Proučavanje bikvadratnih jednačina

Uzmimo bikvadratnu jednačinu

ax 4 + bx 2 + c = 0,

gdje su a, b, c realni brojevi, a a > 0. Uvođenjem pomoćne nepoznate y = x², ispitujemo korijene ove jednadžbe i unosimo rezultate u tabelu (vidi Dodatak br. 1)

2.8 Cardano formula

Ako koristimo modernu simboliku, onda izvođenje Cardano formule može izgledati ovako:

x =

Ova formula određuje korijene opće jednadžbe trećeg stepena:

ax 3 + 3bx 2 + 3cx + d = 0.

Ova formula je vrlo glomazna i složena (sadrži nekoliko složenih radikala). Ne važi uvek, jer. veoma teško završiti.

2.9 Simetrične jednačine trećeg stepena

Simetrične jednačine trećeg stepena nazivaju se jednadžbama oblika

ax³ + bx² + bx + a = 0 ( 1 )

ax³ + bx² - bx - a = 0 ( 2 )

gdje su a i b dati brojevi, a a¹0.

Hajde da pokažemo kako jednačina ( 1 ).

ax³ + bx² + bx + a = a(x³ + 1) + bx(x + 1) = a(x + 1) (x² - x + 1) + bx(x + 1) = (x + 1) (ax² +(b – a)x + a).

Dobijamo da je jednačina ( 1 ) je ekvivalentan jednačini

(x + 1) (ax² +(b - a)x + a) = 0.

Dakle, njegovi korijeni će biti korijeni jednadžbe

ax² +(b - a)x + a = 0

i broj x = -1

jednadžba ( 2 )

ax³ + bx² - bx - a = a(x³ - 1) + bx(x - 1) = a(x - 1) (x² + x + 1) + bx(x - 1) = (x - 1) (ax 2 + ax + a + bx) = (x - 1) (ax² + (b + a)x + a).

1) Primjer :

2x³ + 3x² - 3x - 2 = 0

Jasno je da je x 1 = 1, i

x 2 i x 3 su korijeni jednadžbe 2x² + 5x + 2 = 0,

Pronađimo ih kroz diskriminant:

x 1,2 =

x 2 = -, x 3 = -2

2) Primjer :

5x³ + 21x² + 21x + 5 = 0

Jasno je da je x 1 \u003d -1, i

x 2 i x 3 su korijeni jednadžbe 5x² + 26x + 5 = 0,

Pronađimo ih kroz diskriminant:

x 1,2 =

x 2 = -5, x 3 = -0,2.

2.10 Povratne jednačine

Recipročna jednačina - Algebarska jednačina

a 0 x n + a 1 x n - 1 + ... + a n - 1 x + a n \u003d 0,

u kojem je a k = a n - k, gdje je k = 0, 1, 2 ... n, štoviše, a ≠ 0.

Problem nalaženja korena recipročne jednačine svodi se na problem nalaženja rešenja algebarske jednačine manjeg stepena. Termin recipročne jednačine uveo je L. Euler.

Jednačina četvrtog stepena oblika:

ax 4 + bx 3 + cx 2 + bmx + am² = 0, (a ≠ 0).

Dovođenje ove jednačine u formu

a (x² + m²/x²) + b(x + m/x) + c = 0, i y = x + m/x i y² - 2m = x² + m²/x²,

odakle se jednadžba svodi na kvadrat

ay² + by + (c-2am) = 0.

3x 4 + 5x 3 - 14x 2 - 10x + 12 = 0

Podijelimo ga sa x 2, dobićemo ekvivalentnu jednačinu

3x 2 + 5x - 14 - 5 ×, ili

Gdje i

3(y 2 - 4) + 5y - 14 = 0, odakle

y 1 = y 2 = -2, dakle

I gdje

Odgovor: x 1,2 = x 3,4 =.

Simetrične jednačine su poseban slučaj recipročnih jednačina. Ranije smo govorili o simetričnim jednačinama trećeg stepena, ali postoje i simetrične jednačine četvrtog stepena.

Simetrične jednačine četvrtog stepena.

1) Ako je m = 1, onda je ovo simetrična jednačina prve vrste, koja ima oblik

ax 4 + bx 3 + cx 2 + bx + a = 0 i riješeno novom zamjenom

2) Ako je m = -1, onda je ovo simetrična jednačina druge vrste, koja ima oblik

ax 4 + bx 3 + cx 2 - bx + a = 0 i riješeno novom zamjenom

2.11 Hornerova šema

Za podjelu polinoma primjenjuje se pravilo "podjele ugla" ili Hornerova shema . U tu svrhu, polinomi su raspoređeni u opadajućim stepenima X i pronađite stariji član količnika Q(x) iz uslova da kada se pomnoži sa starijim članom djelitelja D(x), dobije se stariji član dividende P(x). Pronađeni član količnika se množi, zatim sa djeliteljem i oduzima od dividende. Stariji član količnika se određuje iz uslova da, kada se pomnoži sa starijim članom djelitelja, dobije stariji član polinoma razlike itd. Proces se nastavlja sve dok stepen razlike ne bude manji od stepena delioca (vidi Dodatak br. 2).

U slučaju jednačina R = 0, ovaj algoritam je zamijenjen Hornerovom šemom.

Primjer :

x 3 + 4x 2 + x - 6 = 0

Nalazimo djelitelje slobodnog člana ±1; ±2; ± 3; ±6.

Lijevu stranu jednačine označavamo sa f(x). Očigledno, f(1) = 0, x1 = 1. Podijelite f(x) sa x - 1. (Vidi Dodatak br. 3)

x 3 + 4x 2 + x - 6 \u003d (x - 1) (x 2 + 5x + 6)

Posljednji faktor će biti označen sa Q(x). Rješavamo jednačinu Q(x) = 0.

x 2,3 =

Odgovori : 1; -2; -3.

U ovom poglavlju dali smo neke formule za rješavanje različitih jednačina. Većina ovih formula su rješenja određenih jednačina. Ova svojstva su vrlo zgodna, jer je mnogo lakše rješavati jednadžbe koristeći posebnu formulu za ovu jednačinu, a ne prema općem principu. Za svaku metodu dali smo dokaz i nekoliko primjera.

Zaključak

U prvom poglavlju razmatrana je istorija nastanka kvadratnih jednačina i jednačina višeg reda. Razne jednačine su riješene prije više od 25 stoljeća. Mnogi načini za rješavanje takvih jednačina stvoreni su u Babilonu u Indiji. Potreba za jednačinama je bila i biće.

Drugo poglavlje predstavlja različite metode za rješavanje (pronalaženje korijena) kvadratnih jednačina i jednačina višeg reda. U osnovi, to su metode za rješavanje jednadžbi određene prirode, odnosno za svaku grupu jednačina objedinjenih nekim zajedničkim svojstvima ili tipom, dato je posebno pravilo koje vrijedi samo za ovu grupu jednačina. Ova metoda (odabir vlastite formule za svaku jednačinu) je mnogo lakša od pronalaženja korijena preko diskriminanta.

U ovom eseju svi ciljevi su postignuti i glavni zadaci su završeni, nove, do sada nepoznate formule su dokazane i naučene. Radili smo kroz mnoge varijante primjera prije nego što smo ih stavili u sažetak, tako da već znamo kako riješiti neke jednadžbe. Svako rješenje će nam biti od koristi u daljnjim studijama. Ovaj esej je pomogao klasificirati staro znanje i naučiti nova.

Bibliografija

1. Vilenkin N. Ya. “Algebra za 8. razred”, M., 1995.

2. Galitsky M.L. “Zbirka zadataka iz algebre”, M. 2002.

3. Daan-Dalmediko D. “Putevi i lavirinti”, M., 1986.

4. Zvavič L.I. “Algebra 8 razred”, M., 2002.

5. Kushnir I.A. „Jednačine“, Kijev 1996.

6. Savin Yu.P. “Enciklopedijski rečnik mladog matematičara”, M., 1985.

7. Mordkovich A.G. “Algebra 8 razred”, M., 2003.

8. Khudobin A.I. “Zbirka zadataka iz algebre”, M., 1973.

9. Sharygin I.F. “Fakulativni kurs algebre”, M., 1989.

Prilog 1

Proučavanje bikvadratnih jednadžbi

C	b		zaključci
C	b		Na korijenima pomoćne jednadžbe ay² +by+c=0	O korijenima ove jednadžbe a(x²)² +bx² +c=0
C< 0	b- bilo koji realan broj		y< 0 ; y > 0 1 2	x = ±Öy
C > 0	b<0	D > 0		x = ±Öy
		D=0	y > 0	x = ±Öy
		D< 0	nema korijena	nema korijena
	b ≥ 0			nema korijena
			nema korijena	nema korijena
			y > 0 y< 0 1 2	x = ±Öy
C=0	b > 0		y=0	x=0
	b = 0		y=0	x=0
	b< 0		y=0	x=0

Aneks 2

Podjela polinoma polinomom "ugao"

A0	a 1	a 2	...	a n	c
+
b 0 c	b 1 c	…	b n-1 c
B0	b 1	b 2	…	b n	= R (ostatak)

Aneks 3

Hornerova šema

Root
	1	4	1	-6	1
x 1 = 1
demolish	5	6	0
	1	1×1 +4 = 5	5x1 + 1 = 6	6×1 - 6 = 0
root
x 1 = 1

§ 1. Iz istorije nastanka kvadratnih jednačina

2.11 Hornerova šema

Vrlo zanimljivo svojstvo korijena kvadratne jednadžbe otkrio je francuski matematičar Francois Viet. Ovo svojstvo se zove Vietina teorema:

Tako da su brojevi x 1 i x 2 korijeni jednadžbe:

ax² + bx + c = 0

Imamo identitete

Zamjenjujemo jednačinu u formulu za korijene bikvadratnih jednadžbi:

C< 0

y< 0 ; y > 0

1 2

x = ±Öy

x = ±Öy

x = ±Öy

y > 0 y< 0

1 2

x = ±Öy

Možda ćete biti zainteresovani