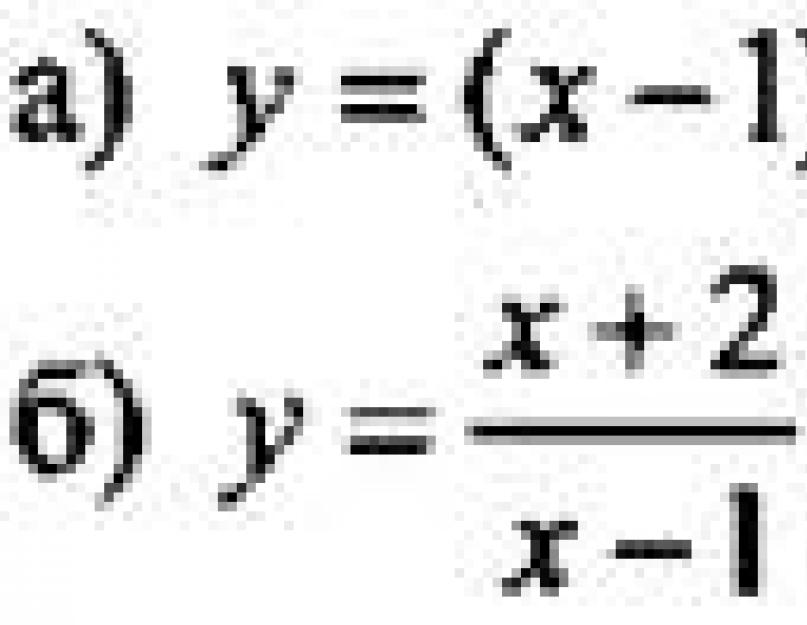transkript

1 Regionalna naučno-praktična konferencija obrazovno-istraživačkog rada učenika 6-11. razreda "Primijenjena i fundamentalna pitanja matematike" Metodološki aspekti proučavanja matematike Konstrukcija grafova funkcija koji sadrže modul Gabova Anzhela Yurievna, 10. razred, MOBU "Gimnazija 3 " Kudymkar, Pikuleva Nadezhda Ivanovna, nastavnik matematike, MOBU "Gymnasium 3", Kudymkar, Perm, 2016.

2 Sadržaj: Uvod...strana 3 I. Glavno tijelo...stranica 6 1.1 Istorijat.. 6 str 2. Osnovne definicije i svojstva funkcija str 2.1 Kvadratna funkcija ..7 str 2.2 Linearna funkcija...8 str 2.3 Frakcijsko-racionalna funkcija 8 str Definicija modula .. 9 str 3.2 Algoritam za crtanje grafa linearne funkcije sa modulom ... 9 str 3.3 Iscrtavanje funkcija koje sadrže "ugniježđene module" u formuli 10 str 3.4 Algoritam za crtanje grafova funkcija oblika y = a 1 x x 1 + a 2 x x a n x x n + ax + b...13 str 3.5 Algoritam za crtanje grafa kvadratne funkcije sa modulom.14 str 3.6 Algoritam za crtanje grafa razlomka racionalne funkcije sa modulom. 15p. 4. Promjene u grafu kvadratne funkcije ovisno o mjestu predznaka apsolutne vrijednosti ..17str. II. Zaključak... 26 str III. Spisak referenci i izvora...27 str IV. Aplikacija....28str. 2

3 Uvod Funkcije crtanja je jedna od njih. zanimljive teme u školskoj matematici. Najveći matematičar našeg vremena, Izrael Mojsejevič Gelfand, napisao je: „Proces crtanja je način pretvaranja formula i opisa u geometrijske slike. Ovo crtanje je sredstvo da vidite formule i funkcije i vidite kako se te funkcije mijenjaju. Na primjer, ako je napisano y = x 2, odmah vidite parabolu; ako je y = x 2-4, vidite parabolu spuštenu za četiri jedinice; ako y = - (x 2 4), tada vidite prethodnu parabolu okrenutu prema dolje. Ova sposobnost da se odjednom vidi formula i njena geometrijska interpretacija važna je ne samo za proučavanje matematike, već i za druge predmete. To je vještina koja ostaje s vama cijeli život, poput učenja vožnje bicikla, kucanja ili vožnje automobila." Osnove rješavanja jednačina sa modulima stekli su u 6. 7. razredu. Odabrao sam upravo ovu temu jer smatram da zahtijeva dublje i temeljitije proučavanje. Želim steći više znanja o modulu broja, različitim načinima crtanja grafova koji sadrže predznak apsolutne vrijednosti. Kada "standardne" jednadžbe linija, parabola, hiperbole uključuju znak modula, njihovi grafovi postaju neobični, pa čak i lijepi. Da biste naučili kako graditi takve grafove, morate savladati tehnike konstruiranja osnovnih figura, kao i čvrsto znati i razumjeti definiciju modula broja. U školskom kursu matematike grafovi sa modulom se ne razmatraju dovoljno detaljno, zbog čega sam želeo da proširim svoja znanja o ovoj temi, da sprovedem sopstveno istraživanje. Bez poznavanja definicije modula, nemoguće je izgraditi čak i najjednostavniji graf koji sadrži apsolutnu vrijednost. karakteristična karakteristika grafovi funkcija koji sadrže izraze sa predznakom modula, 3

4 je prisustvo kinkova u onim tačkama u kojima izraz pod znakom modula mijenja predznak. Svrha rada: razmotriti konstrukciju grafa linearnih, kvadratnih i frakciono racionalnih funkcija koje sadrže promjenljivu pod predznakom modula. Zadaci: 1) Proučiti literaturu o svojstvima apsolutne vrijednosti linearne, kvadratne i frakciono racionalno funkcije. 2) Istražiti promjene u grafovima funkcija ovisno o mjestu predznaka apsolutne vrijednosti. 3) Naučite da crtate grafikone jednačina. Predmet proučavanja: grafovi linearnih, kvadratnih i frakciono racionalnih funkcija. Predmet proučavanja: promjene u grafu linearnih, kvadratnih i frakciono racionalnih funkcija u zavisnosti od položaja predznaka apsolutne vrijednosti. Praktični značaj moj rad je: 1) korišćenje stečenog znanja o temi, kao i njegovo produbljivanje i primena na druge funkcije i jednačine; 2) u korišćenju veština istraživački rad u budućnosti aktivnosti učenja. Relevantnost: Grafički zadaci su tradicionalno jedna od najtežih tema u matematici. Naši maturanti su suočeni sa problemom uspješnog polaganja GIA i Jedinstvenog državnog ispita. Problem istraživanja: crtanje funkcija koje sadrže znak modula iz drugog dijela GIA. Hipoteza istraživanja: aplikacija razvijena na osnovu uobičajeni načini konstruisanjem grafova funkcija koji sadrže znak modula, metode za rešavanje zadataka drugog dela GIA omogućiće studentima da rešavaju ove zadatke 4

5 na svjesnoj osnovi, odabrati najracionalniji metod rješenja, primijeniti različite metode rješenja i uspješnije položiti GIA. Metode istraživanja korištene u radu: 1. Analiza matematičke literature i internet izvora na ovu temu. 2. Reproduktivna reprodukcija proučavanog materijala. 3. Kognitivno-tragačka aktivnost. 4. Analiza i poređenje podataka u potrazi za rješenjem problema. 5. Izjava hipoteza i njihova provjera. 6. Poređenje i generalizacija matematičke činjenice. 7. Analiza dobijenih rezultata. Prilikom pisanja ovog rada korišteni su sljedeći izvori: Internet resursi, OGE testovi, matematička literatura. 5

6 I. Glavni dio 1.1 Istorijska pozadina. U prvoj polovini 17. vijeka koncept funkcije počeo je da se oblikuje kao zavisnost jedne varijable od druge. Dakle, francuski matematičari Pierre Fermat () i Rene Descartes () zamislili su funkciju kao zavisnost ordinate tačke krivulje na njenoj apscisi. A engleski naučnik Isaac Newton () shvatio je funkciju kao koordinatu pokretne tačke koja se mijenja ovisno o vremenu. Termin "funkcija" (od latinskog funkcija performansa, komisija) prvi je uveo njemački matematičar Gottfried Leibniz (). Povezao je funkciju s geometrijskom slikom (grafom funkcije). Kasnije, švicarski matematičar Johann Bernoulli () i član Petersburg Academy Nauke, poznati matematičar iz XVIII vijeka Leonhard Euler () smatrao je funkciju analitičkim izrazom. Ojler takođe ima opšte razumevanje funkcije kao zavisnosti jedne varijable od druge. Riječ "modul" dolazi od latinska reč“modulus”, što u prijevodu znači “mjera”. to polisemanticna rijec(homonim), koji ima mnogo značenja i koristi se ne samo u matematici, već iu arhitekturi, fizici, inženjerstvu, programiranju i dr. egzaktne nauke. U arhitekturi, ovo je početna mjerna jedinica uspostavljena za datu arhitektonsku strukturu i koja se koristi za izražavanje višestrukih omjera njenih sastavni elementi. U inženjerstvu je to pojam koji se koristi u raznim oblastima tehnologije koji nema univerzalno značenje i služi za označavanje različitih koeficijenata i veličina, na primjer, modul zahvata, modul elastičnosti itd. 6

7 Modul volumena (u fizici) je omjer normalnog naprezanja u materijalu i relativnog izduženja. 2.Osnovne definicije i svojstva funkcija Funkcija je jedan od najvažnijih matematičkih pojmova. Funkcija je takva zavisnost varijable y od varijable x, u kojoj svaka vrijednost varijable x odgovara jednoj vrijednosti varijable y. Načini postavljanja funkcije: 1) analitička metoda (funkcija se postavlja pomoću matematičke formule); 2) tabelarni metod (funkcija se specificira pomoću tabele); 3) deskriptivna metoda (funkcija je data verbalnim opisom); četiri) grafički način(funkcija se postavlja pomoću grafikona). Graf funkcije je skup svih točaka koordinatne ravnine, čije su apscise jednake vrijednosti argumenta, a ordinate jednake odgovarajućim vrijednostima funkcije. 2.1 Kvadratna funkcija Funkcija definirana formulom y=ax 2 +in+c, gdje su x i y varijable, a parametri a, b i c su bilo koji realni brojevi, a a = 0, naziva se kvadratnom. Grafikon funkcije y \u003d ax 2 + in + c je parabola; os simetrije parabole y \u003d ax 2 + in + c je prava linija, za a> 0 "grane" parabole su usmjerene prema gore, za a<0 вниз. Чтобы построить график квадратичной функции, нужно: 1) найти координаты вершины параболы и отметить её в координатной плоскости; 2) построить ещё несколько точек, принадлежащих параболе; 3) соединить отмеченные точки плавной линией.,. 2.2Линейная функция функция вида 7

8 (za funkcije jedne varijable). Glavno svojstvo linearnih funkcija je da je povećanje funkcije proporcionalno inkrementu argumenta. To jest, funkcija je generalizacija direktne proporcionalnosti. Graf linearne funkcije je prava linija, otuda i njegovo ime. Ovo se odnosi na realnu funkciju jedne realne varijable. 1) Na, prava linija formira oštar ugao s pozitivnim smjerom x-ose. 2) Kada, linija formira tupi ugao s pozitivnim smjerom x-ose. 3) je indikator ordinate tačke preseka prave sa y-osom. 4) Kada, prava prolazi kroz ishodište. , 2.3 Razlomka-racionalna funkcija je razlomak čiji su brojnik i nazivnik polinomi. Ima oblik gdje, polinomi u bilo kojem broju varijabli. Racionalne funkcije jedne varijable su poseban slučaj: gdje su i polinomi. 1) Svaki izraz koji se može dobiti iz varijabli korištenjem četiri aritmetičke operacije je racionalna funkcija. osam

9 2) Skup racionalnih funkcija je zatvoren pod aritmetičkim operacijama i operacijom kompozicije. 3) Bilo koja racionalna funkcija se može predstaviti kao zbir prostih razlomaka - ovo se koristi u analitičkoj integraciji.., 3. Algoritmi za konstruisanje grafova sa modulom ako je a negativan. a = 3.2 Algoritam za konstruisanje grafa linearne funkcije sa modulom Da biste nacrtali grafove funkcija y= x, morate znati da za pozitivno x imamo x = x. To znači da se za pozitivne vrijednosti argumenta graf y=x poklapa sa grafikom y=x, odnosno ovaj dio grafa je zraka koja izlazi iz ishodišta pod uglom od 45 stepeni u odnosu na x- osa. Za x< 0 имеем x = -x; значит, для отрицательных x график y= x совпадает с биссектрисой второго координатного угла. Впрочем, вторую половину графика (для отрицательных X) легко получить из первой, если заметить, что функция y= x чётная, так как -a = a. Значит, график функции y= x симметричен относительно оси Oy, и вторую половину графика можно приобрести, отразив относительно оси ординат часть, начерченную для положительных x. Получается график:y= x 9

10 Za konstrukciju uzimamo bodove (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2). Sada napravimo graf y= x-1. Ako je A tačka grafikona y= x sa koordinatama (a; a), onda će tačka grafa y= x-1 sa istom vrednošću ordinate Y biti tačka A1 (a+1; a). Ova tačka drugog grafa može se dobiti iz tačke A(a; a) prvog grafa pomeranjem paralelno sa Ox osom udesno. To znači da se cijeli graf funkcije y= x-1 dobija iz grafa funkcije y= x pomjeranjem paralelno s osom Ox udesno za 1. Napravimo grafove: y= x-1 Da bismo izgradili, uzimamo bodove (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1). 3.3 Konstrukcija grafova funkcija koji sadrže "ugniježđene module" u formuli Razmotrimo algoritam konstrukcije na konkretnom primjeru.

11 y \u003d i-2-ix + 5ii 1. Gradimo graf funkcije. 2. Grafikon donje poluravnine prikazujemo prema gore simetrično u odnosu na osu OX i dobijamo grafik funkcije. jedanaest

12 3. Prikazujemo grafik funkcije dolje simetrično oko ose OX i dobijamo grafik funkcije. 4. Prikazujemo grafik funkcije dolje simetrično u odnosu na osu OX i dobijamo grafik funkcije 5. Prikazujemo graf funkcije u odnosu na osu OX i dobijamo grafik. 12

13 6. Kao rezultat, graf funkcije izgleda ovako 3.4. Algoritam za konstruisanje grafova funkcija oblika y = a 1 x x 1 + a 2 x x a n x x n + ax + b. U prethodnom primjeru bilo je dovoljno lako proširiti znakove modula. Ako ima više zbroja modula, onda je problematično razmotriti sve moguće kombinacije znakova izraza podmodula. Kako možemo grafički prikazati funkciju u ovom slučaju? Imajte na umu da je graf polilinija, sa vrhovima u tačkama koje imaju apscise -1 i 2. Za x = -1 i x = 2, izrazi podmodula su jednaki nuli. Na praktičan način pristupili smo pravilu za konstruiranje takvih grafova: Graf funkcije oblika y = a 1 x x 1 + a 2 x x a n x x n + ax + b je polilinija s beskonačnim ekstremnim vezama. Za konstruiranje takve polilinije dovoljno je poznavati sve njene vrhove (apscise vrhova su nule izraza podmodula) i po jednu kontrolnu tačku na lijevoj i desnoj beskonačnoj vezi. 13

14 Zadatak. Nacrtajte funkciju y = x + x 1 + x + 1 i pronađite njenu najmanju vrijednost. Rješenje: 1. Nule izraza podmodula: 0; -jedan; Vrhovi polilinije (0; 2); (-13); (1; 3). (nule izraza podmodula su zamijenjene u jednačinu) Gradimo graf (slika 7), najmanja vrijednost funkcije je Algoritam za crtanje grafa kvadratne funkcije sa modulom Izrada algoritama za pretvaranje grafova funkcija. 1. Konstrukcija grafa funkcije y= f(x). Prema definiciji modula, ova funkcija je dekomponirana na skup od dvije funkcije. Dakle, graf funkcije y= f(x) sastoji se od dva grafika: y= f(x) u desnoj poluravni, y= f(-x) u lijevoj poluravni. Na osnovu toga možemo formulisati pravilo (algoritam). Graf funkcije y= f(x) dobija se iz grafa funkcije y= f(x) na sljedeći način: kod x 0 graf je sačuvan, a kod x< 0полученная часть графика отображается симметрично относительно оси ОУ. 2.Построение графика функции y= f(x). а). Строим график функции y= f(x). б). Часть графика y= f(x), лежащая над осью ОХ, сохраняется, часть его, лежащая под осью ОХ, отображается симметрично относительно оси ОХ. 14

15 3. Da biste napravili graf funkcije y= f(x), prvo morate grafirati funkciju y= f(x) za x> 0, zatim za x< 0 построить изображение, симметричное ему относительно оси ОУ, а затем на интервалах, где f(x) <0,построить изображение, симметричное графику y= f(x) относительно оси ОХ. 4.Для построения графиков вида y = f(x)достаточно построить график функции y= f(x) для тех х из области определения, при которых f(х) 0, и отобразить полученную часть графика симметрично относительно оси абсцисс. Пример Построим график функции у = х 2 6х +5. Сначала построим параболу у= х 2 6х +5. Чтобы получить из неё график функции у = х 2-6х + 5, нужно каждую точку параболы с отрицательной ординатой заменить точкой с той же абсциссой, но с противоположной (положительной) ординатой. Иными словами, часть параболы, расположенную ниже оси Ох, нужно заменить линией, ей симметричной относительно оси Ох (Рис.1). Рис Алгоритм построения графика дробно рациональной функции с модулем 1. Начнем с построения графика В основе его лежит график функции и все мы знаем, как он выглядит: Теперь построим график 15

16 Da biste dobili ovaj graf, dovoljno je samo pomaknuti prethodno dobijeni graf za tri jedinice udesno. Imajte na umu da ako je nazivnik razlomka x + 3, onda bismo pomaknuli graf ulijevo: Sada moramo pomnožiti sa dva sve ordinate da dobijemo graf funkcije Konačno, pomjerimo graf prema gore za dvije jedinice : Zadnje što nam preostaje je da iscrtamo datu funkciju ako je zatvorena pod znakom modula. Da bismo to učinili, reflektujemo simetrično prema gore cijeli dio grafa čije su ordinate negativne (dio koji leži ispod x-ose): Sl.4 16

17 4. Promjene u grafu kvadratne funkcije ovisno o mjestu predznaka apsolutne vrijednosti. Nacrtajte funkciju y = x 2 - x -3 1) Budući da je x = x na x 0, traženi graf se poklapa s parabolom y = 0,25 x 2 - x - 3. Ako je x<0, то поскольку х 2 = х 2, х =-х и требуемый график совпадает с параболой у=0,25 х 2 + х) Если рассмотрим график у=0,25 х 2 - х - 3 при х 0 и отобразить его относительно оси ОУ мы получим тот же самый график. (0; - 3) координаты точки пересечения графика функции с осью ОУ. у =0, х 2 -х -3 = 0 х 2-4х -12 = 0 Имеем, х 1 = - 2; х 2 = 6. (-2; 0) и (6; 0) - координаты точки пересечения графика функции с осью ОХ. Если х<0, ордината точки требуемого графика такая же, как и у точки параболы, но с положительной абсциссой, равной х. Такие точки симметричны относительно оси ОУ(например, вершины (2; -4) и -(2; -4). Значит, часть требуемого графика, соответствующая значениям х<0, симметрична относительно оси ОУ его же части, соответствующей значениям х>0. b) Dakle, I kompletiram za x<0 часть графика, симметричную построенной относительно оси ОУ. 17

18 Fig. 4 Graf funkcije y = f (x) poklapa se s grafom funkcije y = f (x) na skupu nenegativnih vrijednosti argumenta i simetričan je s njim u odnosu na y -os na skupu negativnih vrijednosti argumenta. Dokaz: Ako je x 0, onda je f (x) = f (x), tj. na skupu nenegativnih vrijednosti argumenta, grafovi funkcija y = f (x) i y = f (x) se poklapaju. Budući da je y \u003d f (x) parna funkcija, tada je njen graf simetričan u odnosu na OS. Dakle, graf funkcije y = f (x) može se dobiti iz grafa funkcije y = f (x) na sljedeći način: 1. nacrtati funkciju y = f (x) za x>0; 2. Za x<0, симметрично отразить построенную часть относительно оси ОУ. Вывод: Для построения графика функции у = f (х) 1. построить график функции у = f(х) для х>0; 2. Za x<0, симметрично отразить построенную часть относительно оси ОУ. Построить график функции у = х 2-2х Освободимся от знака модуля по определению Если х 2-2х 0, т.е. если х 0 и х 2, то х 2-2х = х 2-2х Если х 2-2х<0, т.е. если 0<х< 2, то х 2-2х =- х 2 + 2х Видим, что на множестве х 0 и х 2 графики функции у = х 2-2х и у = х 2-2х совпадают, а на множестве (0;2) графики функции у = -х 2 + 2х и у = х 2-2х совпадают. Построим их. График функции у = f (х) состоит из части графика функции у = f(х) при у?0 и симметрично отражённой части у = f(х) при у <0 относительно оси ОХ. Построить график функции у = х 2 - х -6 1) Если х 2 - х -6 0, т.е. если х -2 и х 3, то х 2 - х -6 = х 2 - х

19 Ako je x 2 - x -6<0, т.е. если -2<х< 3, то х 2 - х -6 = -х 2 + х +6. Построим их. 2) Построим у = х 2 - х -6. Нижнюю часть графика симметрично отбражаем относительно ОХ. Сравнивая 1) и 2), видим что графики одинаковые. Работа на тетрадях. Докажем, что график функции у = f (х) совпадает с графиком функции у = f (х) для f(х) >0 i simetrično reflektirani dio y = f (x) na y<0 относительно оси ОХ. Действительно, по определению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий: у = f(х), если f(х) 0; у = - f(х), если f(х) <0 Для любой функции у = f(х), если f(х) >0, zatim f (x) = f (x), što znači da se u ovom dijelu graf funkcije y = f (x) poklapa s grafikom same funkcije y = f (x). Ako je f(x)<0, то f (х) = - f(х),т.е. точка (х; - f(х)) симметрична точке (х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ "отрицательную" часть графика у = f(х). Вывод: действительно для построения графика функции у = f(х) достаточно: 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс. (Рис.5) 19

20 Slika 5. Zaključak: Za iscrtavanje funkcije y= f(x) 1. Grafikon funkcije y=f(x) ; 2. U područjima gdje se graf nalazi u donjoj poluravni, tj. gdje je f(x)<0, строим кривые, симметричные построенным графикам относительно оси абсцисс. (Рис.6, 7.) 20

21 Istraživački rad na crtanju grafova funkcija y = f (x) Koristeći definiciju apsolutne vrijednosti i prethodno razmatrane primjere, crtamo grafove funkcija: y = 2 x - 3 y = x 2-5 x y = x 2-2 i donio zaključke. Da bi se izgradio graf funkcije y = f (x) potrebno je: 1. Izgraditi graf funkcije y = f (x) za x>0. 2. Izgradite drugi dio grafa, tj. odrazite konstruisani graf simetrično u odnosu na OS, jer ova funkcija je parna. 3. Odsječke rezultirajućeg grafa koji se nalaze u donjoj poluravni treba pretvoriti u gornju poluravninu simetrično u odnosu na OX os. Konstruirajte graf funkcije y = 2 x - 3 (1. metoda za određivanje modula) X< -1,5 и х>1,5 a) y = 2x - 3, za x>0 b) za x<0, симметрично отражаем построенную часть относительно оси ОУ. 2. Строим у = -2 х + 3, для 2 х - 3 < 0. т.е. -1,5<х<1,5 а) у = -2х + 3, для х>0 b) za x<0, симметрично отражаем построенную часть относительно оси ОУ. У = 2 х - 3 1) Строим у = 2х-3, для х>0. 2) Pravu liniju gradimo simetričnu onoj izgrađenoj u odnosu na OS os. 3) Dijelovi grafikona koji se nalaze u donjoj poluravni su prikazani simetrično oko ose OX. Upoređujući oba grafikona, vidimo da su isti. 21

22 Primjeri zadataka Primjer 1. Razmotrimo grafik funkcije y = x 2 6x +5. Pošto je x na kvadrat, onda će bez obzira na predznak broja x nakon kvadriranja biti pozitivan. Iz ovoga slijedi da će graf funkcije y = x 2-6x +5 biti identičan grafu funkcije y = x 2-6x +5, tj. graf funkcije koji ne sadrži znak apsolutne vrijednosti (slika 2). Sl.2 Primjer 2. Razmotrite graf funkcije y = x 2 6 x +5. Koristeći definiciju modula broja, zamjenjujemo formulu y \u003d x 2 6 x +5 Sada se bavimo dodjelom ovisnosti po komadima koja nam je dobro poznata. Napravit ćemo graf ovako: 1) izgraditi parabolu y = x 2-6x +5 i zaokružiti taj njen dio, koji je 22

23 odgovara nenegativnim x vrijednostima, tj. dio desno od y-ose. 2) u istoj koordinatnoj ravni konstruiramo parabolu y = x 2 +6x +5 i zaokružimo onaj njen dio koji odgovara negativnim vrijednostima x, tj. dio lijevo od y-ose. Zaokruženi dijelovi parabola zajedno čine graf funkcije y = x 2-6 x +5 (slika 3). Sl.3 Primjer 3. Razmotrite graf funkcije y = x 2-6 x +5. Jer graf jednadžbe y \u003d x 2 6x +5 je isti kao i graf funkcije bez znaka modula (razmatrano u primjeru 2), slijedi da je graf funkcije y = x 2 6 x +5 je identičan grafu funkcije y = x 2 6 x +5, razmatranom u primjeru 2 (slika 3). Primjer 4. Izgradimo graf funkcije y = x 2 6x +5. Da bismo to učinili, konstruiramo graf funkcije y \u003d x 2-6x. Da biste iz njega dobili graf funkcije y \u003d x 2-6x, trebate svaku točku parabole zamijeniti negativnom ordinatom točkom s istom apscisom, ali suprotnom (pozitivnom) ordinatom. Drugim riječima, dio parabole koji se nalazi ispod x-ose mora biti zamijenjen linijom simetričnom oko x-ose. Jer moramo izgraditi graf funkcije y = x 2-6x +5, zatim graf funkcije koju smo razmatrali y = x 2-6x samo treba podići duž y osi za 5 jedinica gore (sl. 4). 23

24 Sl.4 Primjer 5. Napravimo graf funkcije y = x 2-6x + 5. Da bismo to učinili, koristimo dobro poznatu funkciju piecewise. Pronađite nule funkcije y = 6x +5 6x + 5 = 0 at. Razmotrimo dva slučaja: 1) Ako, onda jednačina ima oblik y = x 2 6x -5. Napravimo ovu parabolu i zaokružimo njen dio gdje. 2) Ako, tada jednadžba ima oblik y = x 2 + 6x +5. Napravimo ovu parabolu i zaokružimo njen dio koji se nalazi lijevo od tačke sa koordinatama (slika 5). 24

25 Sl.5 Primjer6. Nacrtajmo funkciju y = x 2 6 x +5. Da bismo to učinili, nacrtat ćemo funkciju y = x 2-6 x +5. Nacrtali smo ovaj graf u primjeru 3. Budući da je naša funkcija potpuno pod znakom modula, da biste nacrtali graf funkcije y = x 2 6 x +5, potrebna vam je svaka tačka grafa funkcije y = x 2 6 x + 5 sa negativnom ordinatom, zamijeniti tačkom sa istom apscisom, ali suprotnom (pozitivnom) ordinatom, tj. dio parabole koji se nalazi ispod ose Ox mora se zamijeniti linijom koja je simetrična u odnosu na osu Ox (slika 6). Fig.6 25

26 II Zaključak „Matematičke informacije mogu se vješto i isplativo koristiti samo ako se kreativno savladaju, tako da učenik sam uvidi kako bi do njih moglo doći samostalno.“ A.N. Kolmogorov. Ovi zadaci su od velikog interesa za učenike devetog razreda, jer su vrlo česti u OGE testovima. Mogućnost izrade ovih grafova funkcija omogućit će vam uspješnije polaganje ispita. Francuski matematičari Pierre Fermat () i Rene Descartes () zamislili su funkciju kao zavisnost ordinate tačke krivulje na njenoj apscisi. A engleski naučnik Isaac Newton () shvatio je funkciju kao koordinatu pokretne tačke koja se mijenja ovisno o vremenu. 26

27 III Spisak referenci i izvora 1. Galitsky M. L., Goldman A. M., Zvavich L. I. Zbirka zadataka iz algebre za 8. 9. razred: Proc. dodatak za učenike škole. i časovi sa produbljivanjem. studija Matematika 2. izd. M .: Prosvjeta, Dorofeev G.V. Matematika. Algebra. Funkcije. Analiza podataka. Ocena 9: m34 Proc. za opšteobrazovne studije. menadžer 2. izd., stereotip. M .: Drfa, Solomonik V. S. Zbirka pitanja i zadataka iz matematike M.: "Viša škola", Yashchenko I.V. GIA. Matematika: tipične ispitne opcije: O opcijama.m .: "Nacionalno obrazovanje", str. 5. Yashchenko I.V. OGE. Matematika: tipične ispitne opcije: O opcijama.m .: "Nacionalno obrazovanje", str. 6. Yashchenko I.V. OGE. Matematika: tipične ispitne opcije: O opcijama.m .: "Nacionalno obrazovanje", str.

28 Dodatak 28

29 Primjer 1. Grafikon funkcije y = x 2 8 x Rješenje. Definirajmo parnost funkcije. Vrijednost za y(-x) je ista kao i vrijednost za y(x), tako da je ova funkcija parna. Tada je njegov graf simetričan u odnosu na osu Oy. Gradimo graf funkcije y = x 2 8x + 12 za x 0 i prikazujemo graf simetrično u odnosu na Oy za negativan x (slika 1). Primjer 2. Sljedeći graf oblika y \u003d x 2 8x To znači da se graf funkcije dobiva na sljedeći način: grade graf funkcije y = x 2 8x + 12, ostavljaju dio grafa koji leži iznad ose Ox nepromijenjen, a dio grafika koji leži ispod ose apscise, prikazan je simetrično u odnosu na os Ox (slika 2). Primjer 3. Za crtanje funkcije y = x 2 8 x + 12, provodi se kombinacija transformacija: y = x 2 8x + 12 y = x 2 8 x + 12 y = x 2 8 x Odgovor : Slika 3. Primjer 4 Izraz koji stoji ispod znaka modula mijenja predznak u tački x=2/3. Na x<2/3 функция запишется так: 29

30 Za x>2/3, funkcija će biti zapisana na sljedeći način: To jest, tačka x=2/3 dijeli našu koordinatnu ravan na dva područja, u jednom od kojih (desno) gradimo funkciju, a u drugi (lijevo) graf funkcije Gradimo: Primjer 5 Dalje je graf također prekinut, ali ima dvije tačke prekida, jer sadrži dva izraza ispod znakova modula:

31 Proširite module na prvom intervalu: Na drugom intervalu: Na trećem intervalu: Dakle, na intervalu (- ; 1.5] imamo graf napisan prvom jednačinom, na intervalu graf napisan drugom jednačinom, i na intervalu)