Svarbi matematikos sąvoka yra funkcija. Su jo pagalba galite vizualiai pavaizduoti daugelį gamtoje vykstančių procesų ir atspindėti ryšį tarp tam tikrų dydžių naudojant formules, lenteles ir vaizdus grafike. Pavyzdys yra skysčio sluoksnio ant kūno slėgio priklausomybė nuo panardinimo gylio, pagreitis nuo tam tikros jėgos veikimo objekte, temperatūros padidėjimas nuo perduodamos energijos ir daugelis kitų procesų. Funkcijos studijavimas apima grafiko sudarymą, jo savybių, apibrėžimo srities ir reikšmių, didėjimo ir mažėjimo intervalų išsiaiškinimą. Svarbus momentasŠiame procese reikia rasti ekstremalių taškų. Toliau kalbėsime apie tai, kaip tai padaryti teisingai.
Apie pačią koncepciją naudojant konkretų pavyzdį
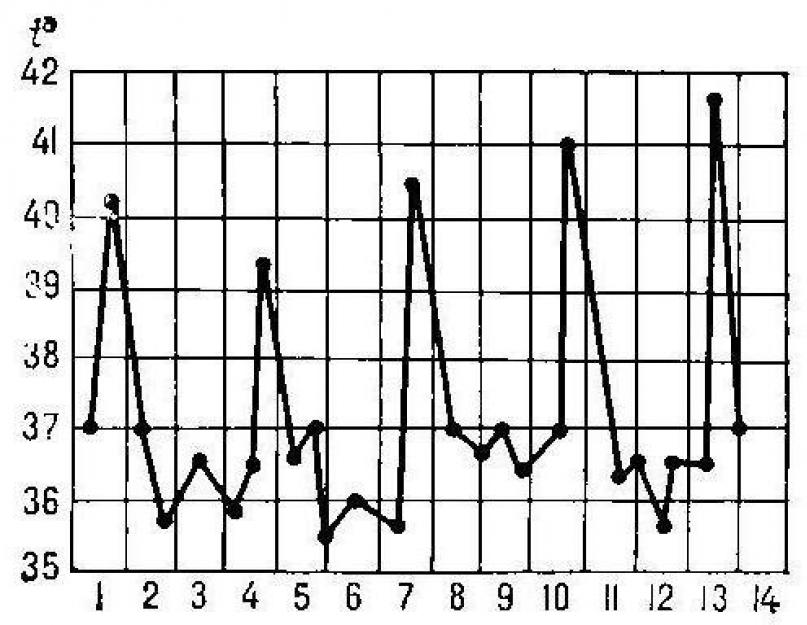
Medicinoje funkcijų grafiko braižymas gali pasakyti apie ligos eigą paciento kūne, aiškiai atspindėdamas jo būklę. Tarkime, kad OX ašis reiškia laiką dienomis, o OU ašis – žmogaus kūno temperatūrą. Paveikslėlyje aiškiai matyti, kaip šis rodiklis smarkiai pakyla, o paskui krenta. Taip pat nesunku pastebėti specialius taškus, atspindinčius momentus, kai funkcija, anksčiau padidėjusi, pradeda mažėti ir atvirkščiai. Tai yra ekstremalūs taškai, ty kritinės vertės (maksimali ir mažiausia) in šiuo atveju paciento temperatūra, po kurios atsiranda jo būklės pokyčiai.

Pasvirimo kampas
Iš paveikslo galite lengvai nustatyti, kaip keičiasi funkcijos išvestinė. Jei grafiko tiesės laikui bėgant kyla aukštyn, tai yra teigiama. Ir kuo jie statesni, tuo didesnę vertę ima išvestinę, kai pasvirimo kampas didėja. Mažėjimo laikotarpiais ši vertė užtrunka neigiamos reikšmės, ekstremumo taškuose virsta nuliu, o išvestinės grafikas pastaruoju atveju brėžiamas lygiagrečiai OX ašiai.
Bet koks kitas procesas turėtų būti traktuojamas taip pat. Tačiau geriausias būdas apibūdinti šią sąvoką yra judėti skirtingi kūnai, aiškiai parodyta diagramose.
Judėjimas
Tarkime, kad objektas juda tiesia linija, tolygiai didindamas greitį. Šiuo laikotarpiu kūno koordinačių kitimas grafiškai pavaizduojamas tam tikra kreive, kurią matematikas vadintų parabolės šaka. Tuo pačiu metu funkcija nuolat didėja, nes koordinačių rodikliai kas sekundę keičiasi vis greičiau. Greičio grafikas rodo išvestinės elgseną, kurios reikšmė taip pat didėja. Tai reiškia, kad judėjimas neturi kritinių taškų.
Tai tęstųsi neribotą laiką. Bet ką daryti, jei kūnas staiga nusprendžia sulėtinti greitį, sustoti ir pradėti judėti kita kryptimi? Tokiu atveju koordinačių rodikliai pradės mažėti. O funkcija perduos kritinę reikšmę ir pereis nuo didėjančios prie mažėjančios.

Naudodamiesi šiuo pavyzdžiu, vėl galite suprasti, kad funkcijos grafike ekstremalūs taškai atsiranda tais momentais, kai ji nustoja būti monotoniška.
Išvestinio fizinė reikšmė
Tai, kas buvo aprašyta anksčiau, aiškiai parodė, kad išvestinė iš esmės yra funkcijos kitimo greitis. Šiame paaiškinime pateikiama jo fizinė reikšmė. Ekstremalūs taškai yra kritinės grafiko sritys. Juos galima identifikuoti ir aptikti apskaičiuojant išvestinės vertės vertę, kuri pasirodo lygi nuliui.
Yra dar vienas požymis, kuris yra pakankama ekstremumo sąlyga. Išvestinė tokiuose vingio taškuose keičia savo ženklą: iš „+“ į „-“ didžiausiame plote ir iš „-“ į „+“ minimaliame plote.

Judėjimas gravitacijos įtakoje
Įsivaizduokime kitą situaciją. Vaikai, žaisdami su kamuoliuku, mėtė jį taip, kad jis pradėjo judėti kampu į horizontą. Iš pradžių greitis šio objekto buvo didžiausias, tačiau veikiamas gravitacijos ėmė mažėti ir su kiekviena sekunde po tiek pat, lygų maždaug 9,8 m/s 2. Tai pagreičio vertė, atsirandanti veikiant žemės traukai laisvojo kritimo metu. Mėnulyje jis būtų maždaug šešis kartus mažesnis.
Kūno judėjimą apibūdinantis grafikas yra parabolė, kurios šakos nukreiptos žemyn. Kaip rasti ekstremalių taškų? Šiuo atveju tai yra funkcijos viršus, kur kūno (rutulio) greitis įgyja nulinę reikšmę. Funkcijos išvestinė tampa lygi nuliu. Tokiu atveju kryptis, taigi ir greičio reikšmė, pasikeičia į priešingą. Kūnas kas sekundę lekia žemyn greičiau, o įsibėgėja tiek pat – 9,8 m/s 2 .

Antrasis darinys
Ankstesniu atveju greičio modulio grafikas brėžiamas kaip tiesi linija. Ši linija iš pradžių nukreipta žemyn, nes šios vertės vertė nuolat mažėja. Vienu momentu pasiekus nulį, šios reikšmės rodikliai pradeda didėti, o greičio modulio grafinio atvaizdavimo kryptis labai pasikeičia. Dabar linija nukreipta į viršų.
Greitis, kuris yra koordinatės išvestinė laiko atžvilgiu, taip pat turi kritinį tašką. Šiame regione funkcija, iš pradžių mažėjanti, pradeda didėti. Tai funkcijos išvestinės ekstremumo taško vieta. Tokiu atveju liestinės polinkio kampas tampa lygus nuliui. O pagreitis, būdamas antrasis koordinatės išvestinis laiko atžvilgiu, keičia ženklą iš „-“ į „+“. Ir judėjimas iš vienodai lėto tampa tolygiai pagreitėjęs.
Pagreičio grafikas
Dabar pažiūrėkime į keturias nuotraukas. Kiekvienas iš jų rodo pokyčių grafiką laikui bėgant, pvz fizinis kiekis, kaip pagreitis. „A“ atveju jo reikšmė išlieka teigiama ir pastovi. Tai reiškia, kad kūno greitis, kaip ir jo koordinatė, nuolat didėja. Jeigu įsivaizduosime, kad objektas taip judės be galo ilgai, tai koordinatės priklausomybę nuo laiko atspindinti funkcija pasirodys nuolatos didėjanti. Iš to išplaukia, kad ji neturi kritinių sričių. Išvestinės grafike taip pat nėra ekstremalių taškų, tai yra tiesiškai kintančio greičio.

Tas pats pasakytina ir apie „B“ atvejį su teigiamu ir nuolat didėjančiu pagreičiu. Tiesa, čia koordinačių ir greičio grafikai bus kiek sudėtingesni.
Kai pagreitis pasiekia nulį
Žvelgiant į „B“ figūrą, galima pastebėti visiškai kitokį vaizdą, apibūdinantį kūno judėjimą. Jo greitis bus grafiškai pavaizduotas parabole, kurios šakos nukreiptos žemyn. Jei tęsiame pagreičio pokytį aprašančią eilutę iki susikirtimo su OX ašimi ir toliau, galime įsivaizduoti, kad iki šios kritinės reikšmės, kur pagreitis pasirodo lygus nuliui, objekto greitis didės vis lėčiau. . Koordinatės funkcijos išvestinės ekstremalus taškas bus tiksliai parabolės viršūnėje, po kurio kūnas radikaliai pakeis savo judėjimo pobūdį ir pradės judėti kita kryptimi.
Paskutiniu atveju „G“ judesio pobūdžio negalima tiksliai nustatyti. Čia žinome tik tai, kad tam tikrą nagrinėjamą laikotarpį nėra pagreičio. Tai reiškia, kad objektas gali likti vietoje arba judėti pastoviu greičiu.
Koordinačių pridėjimo problema
Pereikime prie užduočių, su kuriomis dažnai susiduriama mokantis algebros mokykloje ir kurios siūlomos ruošiantis vieningam valstybiniam egzaminui. Žemiau esančiame paveikslėlyje parodytas funkcijos grafikas. Būtina apskaičiuoti ekstremalių taškų sumą.

Padarykime tai ordinačių ašiai, nustatydami kritinių sričių, kuriose pastebimas funkcijos charakteristikų pokytis, koordinates. Paprasčiau tariant, mes surasime krypčių taškų reikšmes išilgai OX ašies ir tada pereisime prie gautų terminų pridėjimo. Pagal grafiką akivaizdu, kad jie turi tokias reikšmes: -8; -7 ; -5; -3; -2; 1; 3. Tai prideda iki -21, tai yra atsakymas.
Optimalus sprendimas
Nereikia aiškinti, koks svarbus gali būti optimalaus sprendimo pasirinkimas atliekant praktines užduotis. Juk yra daug būdų pasiekti tikslą, tačiau geriausia išeitis, kaip taisyklė, yra tik viena. Tai labai reikalinga, pavyzdžiui, projektuojant laivus, erdvėlaivių ir orlaivių, architektūrinių konstrukcijų, siekiant rasti optimalią šių žmogaus sukurtų objektų formą.

Transporto priemonių greitis labai priklauso nuo tinkamo pasipriešinimo, kurį jos patiria važiuodamos vandeniu ir oru, sumažinimo, nuo perkrovų, atsirandančių veikiant gravitacinėms jėgoms ir daugeliui kitų rodiklių. Laivas jūroje reikalauja tokių savybių kaip stabilumas audros metu upės laivui, svarbu minimali grimzlė. Skaičiuojant optimalų dizainą, kraštutiniai grafiko taškai gali vizualiai suteikti idėją apie geriausią sudėtingos problemos sprendimą. Tokio pobūdžio problemos dažnai išsprendžiamos ekonomikoje, verslo srityse ir daugelyje kitų gyvenimo situacijų.
Iš senovės istorijos
Net senovės išminčiai buvo užimti ekstremaliomis problemomis. Graikų mokslininkai matematiniais skaičiavimais sėkmingai išaiškino plotų ir tūrių paslaptį. Jie pirmieji suprato, kad įvairių figūrų plokštumoje, turinčioje tą patį perimetrą, didžiausias plotas visada turi ratą. Panašiai rutulys turi didžiausią tūrį tarp kitų erdvėje esančių objektų, kurių paviršiaus plotas yra toks pat. Tokių problemų sprendimui atsidavė šie žmonės: garsios asmenybės, kaip Archimedas, Euklidas, Aristotelis, Apolonijus. Heronas puikiai sugebėjo rasti ekstremalių taškų ir, naudodamasis skaičiavimais, sukonstravo išradingus įrenginius. Tai buvo mašinos, judančios garu, siurbliai ir turbinos, veikiančios tuo pačiu principu.

Kartaginos statyba
Yra legenda, kurios siužetas pagrįstas vienos iš ekstremalių problemų sprendimu. Finikiečių princesės, kuri kreipėsi pagalbos į išminčius, pademonstruoto verslo požiūrio rezultatas buvo Kartaginos statyba. Žemės sklypasšiam senoviniam ir garsiam miestui Dido (toks buvo valdovo vardas) davė vienos iš Afrikos genčių vadas. Sklypo plotas iš pradžių jam neatrodė labai didelis, nes pagal sutartį jis turėjo būti padengtas jaučio oda. Tačiau princesė įsakė savo kareiviams supjaustyti jį plonomis juostelėmis ir iš jų padaryti diržą. Jis pasirodė toks ilgas, kad apėmė plotą, kuriame tilpo visas miestas.
Matematinės analizės ištakos
O dabar pereikime nuo seniausių laikų į naujesnę erą. Įdomu tai, kad Keplerį suprasti matematinės analizės pagrindus XVII amžiuje paskatino susitikimas su vyno pardavėju. Prekybininkas taip išmanė savo profesiją, kad nesunkiai galėjo nustatyti gėrimo tūrį statinėje tiesiog nuleidęs į ją geležinę virvę. Apmąstydamas tokį kuriozą, žinomas mokslininkas sugebėjo išspręsti šią dilemą. Pasirodo, įgudę tų laikų kuprininkai įprato gaminti indus taip, kad tam tikrame tvirtinimo žiedų perimetro aukštyje ir spinduliu jie turėjo maksimalią talpą.
Tai tapo priežastimi Kepleriui galvoti toliau. Kuprininkai iki optimalaus sprendimo priėjo per ilgas paieškas, klaidas ir naujus bandymus, perduodant savo patirtį iš kartos į kartą. Tačiau Kepleris norėjo pagreitinti procesą ir išmokti per trumpą laiką atlikti tą patį per matematinius skaičiavimus. Visi jo pokyčiai, kuriuos perėmė jo kolegos, virto dabar žinomomis Fermato ir Niutono-Leibnizo teoremomis.
Didžiausio ploto problema
Įsivaizduokime, kad turime vielą, kurios ilgis yra 50 cm. Kaip iš jo padaryti didžiausio ploto stačiakampį?
Priimdami sprendimą, turėtumėte vadovautis paprastomis, visiems žinomomis tiesomis. Akivaizdu, kad mūsų figūros perimetras bus 50 cm. Jis sudarytas iš dvigubo abiejų pusių ilgio. Tai reiškia, kad vieną iš jų pažymėjus „X“, kitą galima išreikšti kaip (25 - X).
Iš čia gauname plotą, lygų X(25 - X). Ši išraiška gali būti laikoma funkcija, kuri turi kelias reikšmes. Norint išspręsti problemą, reikia rasti jų maksimumą, vadinasi, reikia išsiaiškinti kraštutinius taškus.
Norėdami tai padaryti, randame pirmąją išvestinę ir prilygstame nuliui. Rezultatas yra paprasta lygtis: 25 - 2X = 0.
Iš jo sužinome, kad viena iš kraštinių yra X = 12,5.
Todėl kitas: 25 - 12,5 = 12,5.
Pasirodo, kad problemos sprendimas bus kvadratas, kurio kraštinė yra 12,5 cm.

Kaip rasti maksimalų greitį
Pažvelkime į kitą pavyzdį. Įsivaizduokime, kad yra kūnas, kurio tiesinį judėjimą apibūdina lygtis S = - t 3 + 9t 2 - 24t - 8, kur nuvažiuotas atstumas išreiškiamas metrais, o laikas - sekundėmis. Turime rasti maksimalų greitį. Kaip tai padaryti? Atsisiuntę randame greitį, tai yra pirmąją išvestinę.
Gauname lygtį: V = - 3t 2 + 18t - 24. Dabar, norėdami išspręsti problemą, vėl turime rasti ekstremumo taškus. Tai turi būti padaryta taip pat, kaip ir ankstesnėje užduotyje. Randame pirmąją greičio išvestinę ir prilygstame nuliui.
Gauname: - 6t + 18 = 0. Vadinasi, t = 3 s. Tai laikas, kai kūno greitis įgauna kritinę reikšmę. Gautus duomenis pakeičiame į greičio lygtį ir gauname: V = 3 m/s.
Bet kaip suprasti, kas tai yra? maksimalus greitis, nes kritiniais funkcijos taškais gali būti jos didžiausios arba mažiausios reikšmės? Norėdami patikrinti, turite rasti antrąjį greičio išvestinį. Jis išreiškiamas kaip skaičius 6 su minuso ženklu. Tai reiškia, kad rastas taškas yra maksimalus. O esant teigiamai reikšmei, antroji išvestinė turėtų minimumą. Tai reiškia, kad rastas sprendimas pasirodė teisingas.
Kaip pavyzdys pateiktos problemos yra tik dalis tų, kurias galima išspręsti, jei žinote, kaip rasti funkcijos kraštutinius taškus. Tiesą sakant, jų yra daug daugiau. Ir tokios žinios žmogaus civilizacijai atveria neribotas galimybes.
Kaip matote, šis funkcijos ekstremumo ženklas reikalauja, kad taške būtų bent jau antros eilės išvestinė.
Pavyzdys.
Raskite funkcijos kraštutinumą.
Sprendimas.
Pradėkime nuo apibrėžimo srities: 
Atskirkime pradinę funkciją: 
x=1, tai yra galimo ekstremumo taškas. Randame antrąją funkcijos išvestinę ir apskaičiuojame jos reikšmę ties:

x = 1 x=1 Todėl pagal antrąją pakankamą ekstremumo sąlygą,  - maksimalus taškas. Tada
- maksimalus taškas. Tada
- maksimali funkcija.

Grafinė iliustracija.
![]()
Atsakymas:
Trečioji pakankama funkcijos ekstremumo sąlyga. Tegul funkcija y=f(x) turi išvestinių priemonių iki n -toji eilės taško kaimynystėje ir vediniai iki n+1
Pavyzdys.
-toji tvarka pačiame taške. Tebūnie. ![]() .
.
Sprendimas.
Raskite funkcijos kraštutinius taškus
Pradinė funkcija yra racionali visa funkcija, kurios apibrėžimo sritis yra visa realiųjų skaičių rinkinys. 
Išskirkime funkciją: ![]() , todėl tai yra galimo ekstremumo taškai. Panaudokime trečią pakankamą ekstremumo sąlygą.
, todėl tai yra galimo ekstremumo taškai. Panaudokime trečią pakankamą ekstremumo sąlygą.
Randame antrąją išvestinę ir apskaičiuojame jos reikšmę galimo ekstremumo taškuose (tarpinius skaičiavimus praleisime): 
Vadinasi, yra maksimalus taškas (už trečią pakankamą ekstremumo ženklą turime n=1 Ir).
Norėdami išsiaiškinti taškų prigimtį ![]() randame trečiąją išvestinę ir apskaičiuojame jos vertę šiuose taškuose:
randame trečiąją išvestinę ir apskaičiuojame jos vertę šiuose taškuose: 
Todėl yra funkcijos vingio taškas ( n=2 Ir).
Belieka susitvarkyti su esme. Mes randame ketvirtąją išvestinę ir apskaičiuojame jos vertę šioje vietoje: 
Todėl yra mažiausias funkcijos taškas.
- maksimali funkcija.

Grafinė iliustracija.
Maksimalus taškas yra mažiausias funkcijos taškas.
10. Funkcijos ekstremumas Ekstremo apibrėžimas
Iškviečiama funkcija y = f(x). didėja (mažėja) tam tikru intervalu, jei x 1< x 2 выполняется неравенство (f(x 1) < f (x 2) (f(x 1) >f(x 2)).
Jei diferencijuojama funkcija y = f(x) didėja (mažėja) intervale, tai jos išvestinė šiame intervale f " (x) 0
(f " (x) 0).
Taškas x O paskambino vietinis maksimalus taškas (minimumas) funkcija f(x), jei yra taško kaimynystė x O, visiems taškams, kurių nelygybė f(x) ≤ f(x о) (f(x) ≥ f(x о)) yra teisinga.
Vadinami didžiausi ir mažiausi taškai ekstremalūs taškai, o funkcijos reikšmės šiuose taškuose yra jos kraštutinumai.
Ekstremalūs taškai
Būtinos sąlygos ekstremumui. Jei taškas x O yra funkcijos f(x) ekstremumo taškas, tada arba f " (x o) = 0, arba f (x o) neegzistuoja. Tokie taškai vadinami kritiškas, o pati funkcija apibrėžiama kritiniame taške. Funkcijos kraštutinumo reikia ieškoti tarp jos kritinių taškų.
Pirma pakankama sąlyga. Leiskite x O- kritinis taškas. Jei f "(x), kai eina per tašką x O pakeičia pliuso ženklą į minusą, tada taške x O funkcija turi maksimumą, kitu atveju turi minimumą. Jei, einant per kritinį tašką, išvestinė ženklo nekeičia, tai taške x O ekstremalaus nera.
Antra pakankama sąlyga. Tegul funkcija f(x) turi išvestinę f " (x) netoli taško x O o antroji išvestinė pačiame taške x O. Jei f "(x o) = 0, >0 (<0), то точка x O yra funkcijos f(x) lokalus minimumas (maksimalus) taškas. Jei =0, tuomet reikia arba naudoti pirmąją pakankamą sąlygą, arba naudoti aukštesnes išvestines.
Atkarpoje funkcija y = f(x) gali pasiekti mažiausią arba didžiausią reikšmę kritiniuose taškuose arba atkarpos galuose.
3.22 pavyzdys. Raskite funkcijos f(x) = 2x 3 - 15x 2 + 36x - 14 ekstremalumą.
Sprendimas. Kadangi f "(x) = 6x 2 - 30x +36 = 6(x -2)(x - 3), tada kritiniai funkcijos x 1 = 2 ir x 2 = 3 taškai. Ekstrema gali būti tik ties Taigi, kai eidama per tašką x 1 = 2, išvestinė pakeičia savo ženklą iš pliuso į minusą, tai šiame taške funkcija turi maksimumą į pliusą, todėl taške x 2 = 3 funkcija turi minimumą Apskaičiavę funkcijos reikšmes taškuose x 1 = 2 ir x 2 = 3, randame funkcijos ekstremalą: maksimalus f(. 2) = 14 ir mažiausias f(3) = 13.
Apsvarstykite tolydžios funkcijos grafiką Tegul funkcija parodyta paveiksle.
Funkcijos reikšmė taške x 1 bus didesnė už funkcijų reikšmes visuose gretimuose taškuose tiek kairėje, tiek dešinėje x 1. Šiuo atveju sakome, kad funkcija turi tašką x 1 daugiausiai. Taške x Akivaizdu, kad 3 funkcija taip pat turi maksimumą. Jei svarstysime esmę x 2, tada funkcijos reikšmė jame yra mažesnė už visas gretimas reikšmes. Šiuo atveju sakome, kad funkcija turi tašką x 2 minimum. Lygiai taip pat dėl reikalo x 4 .
Funkcija Tegul funkcija taške x 0 turi maksimalus, jei funkcijos reikšmė šiame taške yra didesnė už jos reikšmes visuose tam tikro intervalo, kuriame yra taškas, taškuose x 0, t.y. jei yra tokia taško kaimynystė x 0, kuris tinka visiems x≠x 0 , priklausantis šiai apylinkei, nelygybė galioja f(x)<f(x 0 ) .
Funkcija Tegul funkcija turi minimumas taške x 0 , jei yra tokia taško kaimynystė x 0 , tai visiems x≠x 0, priklausančių šiai apylinkei, galioja nelygybė f(x)>f(x 0.
Taškai, kuriuose funkcija pasiekia maksimumą ir minimumą, vadinami ekstremumais, o funkcijos reikšmės šiuose taškuose – funkcijos ekstremumais.
Atkreipkime dėmesį į tai, kad atkarpoje apibrėžta funkcija savo maksimumą ir minimumą gali pasiekti tik taškuose, esančiuose nagrinėjamoje atkarpoje.
Atkreipkite dėmesį, kad jei funkcija taške turi maksimumą, tai nereiškia, kad tuo momentu funkcija turi didžiausią reikšmę visoje apibrėžimo srityje. Aukščiau aptartame paveikslėlyje funkcija taške x 1 turi maksimumą, nors yra taškų, kuriuose funkcijos reikšmės yra didesnės nei taške x 1 . Visų pirma, f(x 1) < f(x 4) t.y. funkcijos minimumas yra didesnis už maksimumą. Iš maksimumo apibrėžimo tik išplaukia, kad tai yra didžiausia funkcijos reikšmė pakankamai arti maksimalaus taško.
1 teorema. (Būtina ekstremumo egzistavimo sąlyga.) Jei diferencijuojamoji funkcija Tegul funkcija turi taške x=x 0 ekstremumas, tada jo išvestinė šiame taške tampa nuliu.
Įrodymas. Leiskite, aiškumo dėlei, taške x 0 funkcija turi maksimumą. Tada pakankamai mažiems žingsniams Δ x mes turime f(x 0 + Δ x)
Pereinant šias nelygybes į ribą ties Δ x→ 0 ir atsižvelgiant į tai, kad išvestinė f "(x 0) egzistuoja, todėl riba kairėje nepriklauso nuo to, kaip Δ x→ 0, gauname: ties Δ x → 0 – 0 f"(x 0) ≥ 0 a ties Δ x → 0 + 0 f"(x 0) ≤ 0. Kadangi f"(x 0) apibrėžia skaičių, tada šios dvi nelygybės yra suderinamos tik jei f"(x 0) = 0.
Įrodyta teorema teigia, kad didžiausią ir mažiausią tašką galima rasti tik tarp tų argumento reikšmių, kuriose išvestinė tampa lygi nuliu.
Mes nagrinėjome atvejį, kai funkcija turi išvestinę visuose tam tikros atkarpos taškuose. Kokia situacija yra tais atvejais, kai išvestinė priemonė neegzistuoja? Pažiūrėkime į pavyzdžius.
Pavyzdžiai.
- y=|x|.
Funkcija taške neturi išvestinės x=0 (šiuo taške funkcijos grafikas neturi apibrėžtos liestinės), tačiau šioje vietoje funkcija turi minimumą, nes y(0) = 0 ir visiems x≠ 0y > 0.
- Leiskite x< x
0 . Tada c< x
0 ir f "(c)> 0.
Štai kodėl f "(c)(x-x 0)<
0 ir todėl
f(x) – f(x 0 )< 0, t.y. f(x)< f(x 0 ).
- Leiskite x > x 0 . Tada c>x 0 ir f "(c)< 0. Reiškia f "(c)(x-x 0)< 0. Štai kodėl f(x) – f(x 0 ) <0,т.е.f(x)< f(x 0 ) .
- Raskite funkcijos sritį f(x).
- Raskite pirmąją funkcijos išvestinę f "(x).
- Nustatykite kritinius taškus:
- rasti tikrąsias lygties šaknis f "(x)=0;
- rasti visas vertybes x kuriam išvestinė f "(x) neegzistuoja.
- Nustatykite išvestinės kritinio taško kairėje ir dešinėje ženklą. Kadangi išvestinės ženklas išlieka pastovus tarp dviejų kritinių taškų, pakanka nustatyti išvestinės ženklą viename taške į kairę ir vienu tašku į dešinę nuo kritinio taško.
- Apskaičiuokite funkcijos reikšmę ekstremaliuose taškuose.
- Raskite visus kritinius funkcijos taškus intervale ( a, b) ir apskaičiuokite funkcijų reikšmes šiuose taškuose.
- Apskaičiuokite funkcijos reikšmes segmento galuose, kai x = a, x = b.
- Iš visų gautų verčių pasirinkite didžiausią ir mažiausią.

Funkcija neturi išvestinės at x=0, nes jis eina į begalybę ties x=0. Tačiau šiuo metu funkcija turi maksimumą.
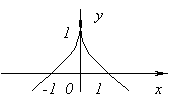
Funkcija neturi išvestinės at x=0, nuo ![]() adresu x→0. Šiuo metu funkcija neturi nei maksimumo, nei minimumo. tikrai, f(x)=0 ir at x<0f(x)<0, а при x>0f(x)>0.
adresu x→0. Šiuo metu funkcija neturi nei maksimumo, nei minimumo. tikrai, f(x)=0 ir at x<0f(x)<0, а при x>0f(x)>0.

Taigi iš pateiktų pavyzdžių ir suformuluotos teoremos aišku, kad funkcija ekstremumą gali turėti tik dviem atvejais: 1) taškuose, kur išvestinė egzistuoja ir lygi nuliui; 2) taške, kur darinys neegzistuoja.
Tačiau jei tam tikru momentu x 0 mes tai žinome f "(x 0 ) =0, tada iš to negalima daryti išvados, kad taške x 0 funkcija turi ekstremumą.
Pavyzdžiui. ![]() .
.

Bet laikotarpis x=0 nėra ekstremumo taškas, nes šio taško kairėje funkcijos reikšmės yra žemiau ašies Jautis, o viršuje dešinėje.
Argumento reikšmės iš funkcijos srities, kurioje funkcijos išvestinė išnyksta arba neegzistuoja, vadinamos kritinius taškus.
Iš viso to, kas išdėstyta pirmiau, išplaukia, kad funkcijos ekstremalūs taškai yra tarp kritinių taškų, tačiau ne kiekvienas kritinis taškas yra ekstremumo taškas. Todėl, norėdami rasti funkcijos ekstremumą, turite rasti visus svarbiausius funkcijos taškus, o tada kiekvieną iš šių taškų atskirai išnagrinėti, kad būtų nustatytas maksimalus ir minimumas. Šiam tikslui pasitarnauja sekanti teorema.
2 teorema. (Pakankama sąlyga ekstremumui egzistuoti.) Tegul funkcija yra ištisinė tam tikrame intervale, kuriame yra kritinis taškas x 0, ir yra diferencijuojamas visuose šio intervalo taškuose (išskyrus, galbūt, patį tašką x 0). Jei, judant iš kairės į dešinę per šį tašką, išvestinė keičia ženklą iš pliuso į minusą, tai taške x = x 0 funkcija turi maksimumą. Jei, pravažiuojant x 0 iš kairės į dešinę, išvestinė keičia ženklą iš minuso į pliusą, tada funkcija šiuo metu turi minimumą.
Taigi, jei
Įrodymas. Pirmiausia manykime, kad pravažiuojant x 0 išvestinė keičia ženklą iš pliuso į minusą, t.y. visų akivaizdoje x, arti taško x 0 f "(x)> 0 už x< x 0 , f "(x)< 0 už x>x 0 . Skirtumui pritaikykime Lagranžo teoremą f(x) – f(x 0 ) = f "(c)(x-x 0), kur c yra tarp x Ir x 0 .
Taigi visoms vertybėms x pakankamai arti x 0 f(x)< f(x 0 ) . Ir tai reiškia, kad taške x 0 funkcija turi maksimumą.
Antroji minimalios teoremos dalis įrodyta panašiai.
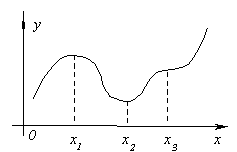
Iliustruojame šios teoremos reikšmę paveiksle. Leiskite f "(x 1 ) =0 ir bet kuriai x, pakankamai arti x 1, nelygybės tenkinamos
f "(x)< 0 val x< x 1 , f "(x)> 0 val x>x 1 .
Tada į kairę nuo taško x 1 funkcija dešinėje didėja ir mažėja, todėl kai x = x 1 funkcija pereina nuo didėjančios prie mažėjančios, tai yra, ji turi maksimumą.
Panašiai galime apsvarstyti taškus x 2 ir x 3 .

Visa tai, kas išdėstyta pirmiau, gali būti schematiškai pavaizduota paveikslėlyje:
Ekstremumo funkcijos y=f(x) tyrimo taisyklė
Pavyzdžiai. Ištirkite minimalias ir maksimalias funkcijas.
DIDŽIAUSIOS IR MAŽIAUSIOS FUNKCIJOS segmente VERTĖS
Didžiausias funkcijos reikšmė intervale yra didžiausia iš visų jos verčių šiame intervale ir mažiausias– pati mažiausia iš visų savo vertybių.
Apsvarstykite funkciją Tegul funkcija ištisinis segmente [ a, b]. Kaip žinoma, tokia funkcija pasiekia didžiausias ir minimalias reikšmes arba ties atkarpos riba, arba jos viduje. Jei didžiausia arba mažiausia funkcijos reikšmė pasiekiama vidiniame atkarpos taške, tai ši reikšmė yra maksimali arba mažiausia funkcijos, tai yra, ji pasiekiama kritiniuose taškuose.
Taigi gauname štai ką taisyklė, kaip rasti didžiausią ir mažiausią funkcijos reikšmes segmente[ a, b] :
Funkcijos padidėjimas, sumažėjimas ir ekstremumai
Funkcijos didėjimo, mažėjimo ir ekstremalių intervalų nustatymas yra ir savarankiška užduotis, ir esminė kitų užduočių dalis, ypač pilnas funkcijų tyrimas. Pateikiama pradinė informacija apie funkcijos padidėjimą, sumažėjimą ir kraštutinumus teorinis skyrius apie išvestinę, kurią labai rekomenduoju išankstiniam tyrimui (arba kartojimas)– taip pat dėl to, kad ši medžiaga yra pagrįsta pačia iš esmės išvestinė, yra harmoningas šio straipsnio tęsinys. Nors, jei laiko mažai, galima ir grynai formaliai praktikuoti pavyzdžius iš šios dienos pamokos.
Ir šiandien ore tvyro reto vieningumo dvasia, ir aš tiesiogiai jaučiu, kad visi esantys dega noru išmokti tyrinėti funkciją naudojant jos išvestinę. Todėl jūsų monitoriaus ekranuose iš karto atsiranda protinga, gera, amžina terminija.
Už ką? Viena iš priežasčių yra pati praktiškiausia: kad būtų aišku, ko iš jūsų paprastai reikalaujama atliekant tam tikrą užduotį!
Funkcijos monotoniškumas. Funkcijos ekstremumai ir ekstremumai
Panagrinėkime kai kurias funkcijas. Paprasčiau tariant, manome, kad ji tęstinis visoje skaičių eilutėje:

Tik tuo atveju iš karto atsikratykime galimų iliuzijų, ypač tiems skaitytojams, kurie neseniai susipažino funkcijos pastovaus ženklo intervalai. Dabar mes NEĮdomu, kaip funkcijos grafikas yra ašies atžvilgiu (viršuje, apačioje, kur ašis susikerta). Kad įtikintumėte, mintyse ištrinkite ašis ir palikite vieną grafiką. Nes čia ir slypi susidomėjimas.
Funkcija didėja intervale, jei bet kuriuose dviejuose šio intervalo taškuose, sujungtuose santykiu , nelygybė yra teisinga. Tai reiškia, kad didesnė argumento reikšmė atitinka didesnę funkcijos reikšmę, o jos grafikas eina „iš apačios į viršų“. Per laikotarpį demonstravimo funkcija auga.
Taip pat ir funkcija mažėja apie intervalą, jei bet kurių dviejų taškų tam tikro intervalo toks, kad , Nelygybė yra tiesa. Tai reiškia, kad didesnė argumento reikšmė atitinka mažesnę funkcijos reikšmę, o jos grafikas eina „iš viršaus į apačią“. Mūsų funkcija mažėja intervalais ![]() .
.
Jei funkcija didėja arba mažėja per intervalą, tada ji vadinama griežtai monotoniškasšiuo intervalu. Kas yra monotonija? Supraskite tai pažodžiui – monotonija.
Taip pat galite apibrėžti nemažėjantis funkcija (atsipalaidavusi būsena pirmajame apibrėžime) ir nedidėjantis funkcija (suminkštinta sąlyga 2-oje apibrėžime). Nemažėjanti arba nedidėjanti intervalo funkcija vadinama monotonine tam tikro intervalo funkcija (griežtas monotoniškumas yra ypatingas „paprasčiausio“ monotoniškumo atvejis).
Teorija taip pat svarsto kitus funkcijos padidėjimo/sumažėjimo nustatymo būdus, įskaitant pusintervalus, segmentus, tačiau kad nepiltume ant galvos aliejus-alyva-alyva, sutiksime operuoti atvirais intervalais su kategoriškais apibrėžimais. - tai yra aiškiau ir gana daug praktinių problemų išspręsti.
Taigi, mano straipsniuose formuluotė „funkcijos monotoniškumas“ beveik visada bus paslėpta intervalais griežta monotonija(griežtai didėjanti arba griežtai mažėjanti funkcija).
Taško kaimynystė. Žodžiai, po kurių mokiniai bėga kur tik gali ir iš siaubo slepiasi kampuose. ...Nors po įrašo Cauchy ribos Tikriausiai jie jau nebeslepia, o tik šiek tiek dreba =) Nesijaudink, dabar nebus matematinės analizės teoremų įrodymų – reikėjo aplinkos, kad apibrėžimai būtų griežčiau suformuluoti ekstremalūs taškai. Prisiminkime:
Taško kaimynystė vadinamas intervalas, kuriame yra duotas taškas, o patogumo dėlei intervalas dažnai laikomas simetrišku. Pavyzdžiui, taškas ir jo standartinė kaimynystė:
Tiesą sakant, apibrėžimai:
Taškas vadinamas griežtas maksimalus taškas, Jei egzistuoja jos kaimynystėje, visiems kurių vertės, išskyrus patį tašką, nelygybė . Mūsų konkrečiame pavyzdyje tai yra taškas.
Taškas vadinamas griežtas minimalus taškas, Jei egzistuoja jos kaimynystėje, visiems kurių vertės, išskyrus patį tašką, nelygybė . Brėžinyje yra taškas „a“.
Pastaba : kaimynystės simetrijos reikalavimas visai nebūtinas. Be to, svarbu pats egzistavimo faktas kaimynystė (maža ar mikroskopinė), atitinkanti nurodytas sąlygas
Taškai vadinami griežtai ekstremalūs taškai arba tiesiog ekstremalūs taškai funkcijas. Tai yra apibendrintas maksimalaus ir minimalaus balo terminas.
Kaip suprantame žodį „ekstremalus“? Taip, taip pat tiesiogiai kaip monotonija. Ekstremalūs kalnelių taškai.
Kaip ir monotoniškumo atveju, laisvi postulatai egzistuoja ir teoriškai yra dar labiau paplitę (kurios, žinoma, patenka į griežtus atvejus!):
Taškas vadinamas maksimalus taškas, Jei egzistuoja jo aplinka yra tokia visiems
Taškas vadinamas minimalus taškas, Jei egzistuoja jo aplinka yra tokia visiemsšios kaimynystės vertybes, nelygybė galioja.
Atkreipkite dėmesį, kad pagal paskutinius du apibrėžimus bet kuris pastovios funkcijos taškas (arba funkcijos „plokščia atkarpa“) laikomas ir maksimaliu, ir mažiausiu tašku! Funkcija, beje, yra ir nedidinanti, ir nemažinanti, tai yra monotoniška. Tačiau šiuos svarstymus paliksime teoretikams, nes praktiškai beveik visada kontempliuojame tradicines „kalvas“ ir „daubas“ (žr. brėžinį) su unikaliu „kalno karaliumi“ arba „pelkės princese“. Kaip įvairovė pasitaiko patarimas, nukreiptas aukštyn arba žemyn, pavyzdžiui, funkcijos minimumas taške.
O, o kalbant apie honorarą:
– vadinasi prasmė maksimalus funkcijos;
– vadinasi prasmė minimumas funkcijas.
Bendras pavadinimas - kraštutinumai funkcijas.
Būkite atsargūs su savo žodžiais!
Ekstremalūs taškai– tai yra „X“ reikšmės.
Kraštutinumai– „žaidimo“ reikšmės.
! Pastaba : kartais išvardyti terminai nurodo „X-Y“ taškus, kurie yra tiesiogiai PATSIOS funkcijos GRAFĖJE.
Kiek ekstremalių gali turėti funkcija?
Nėra, 1, 2, 3 ir tt ad begalybės. Pavyzdžiui, sinusas turi be galo daug minimumų ir maksimumų.
SVARBU! Terminas „maksimali funkcija“ ne tapatus terminas „didžiausia funkcijos reikšmė“. Nesunku pastebėti, kad vertė yra maksimali tik vietiniame rajone, o viršuje kairėje yra „šaltesni bendražygiai“. Taip pat „funkcijos minimumas“ nėra tas pats, kas „minimali funkcijos reikšmė“, o brėžinyje matome, kad reikšmė yra minimali tik tam tikroje srityje. Šiuo atžvilgiu taip pat vadinami ekstremumo taškai vietiniai ekstremumo taškai o ekstremumai – vietiniai kraštutinumai. Jie vaikšto ir klaidžioja netoliese ir globalus broliai. Taigi, bet kuri parabolė turi savo viršūnę pasaulinis minimumas arba pasaulinis maksimumas. Be to, aš neskirsiu kraštutinumų tipų, o paaiškinimas išsakomas labiau bendrais ugdymo tikslais - papildomi būdvardžiai „vietinis“ / „pasaulinis“ neturėtų jus nustebinti.
Apibendrinkime trumpą teorijos apžvalgą bandomuoju šūviu: ką reiškia užduotis „rasti funkcijos monotoniškumo intervalus ir ekstremalumo taškus“?
Formuluotė skatina jus rasti:
– didėjančios/mažėjančios funkcijos intervalai (nemažėjanti, nedidėjanti atsiranda daug rečiau);
– maksimalus ir (arba) minimalus balas (jei yra). Na, o kad nepasisektų, geriau susirasti minimumus/maksimumus patiems ;-)
Kaip visa tai nustatyti? Naudojant išvestinę funkciją!
Kaip rasti didėjimo, mažėjimo intervalus,
funkcijos ekstremumai ir ekstremumai?
Iš tikrųjų daugelis taisyklių jau žinomos ir suprantamos pamoka apie vedinio reikšmę.
Tangentinė išvestinė ![]() atneša linksmų naujienų, kad funkcija vis didėja apibrėžimo sritis.
atneša linksmų naujienų, kad funkcija vis didėja apibrėžimo sritis.
Su kotangentu ir jo išvestine ![]() situacija yra visiškai priešinga.
situacija yra visiškai priešinga.
Arsinusas didėja per intervalą - išvestinė čia yra teigiama: ![]() .
.
Kai funkcija apibrėžta, bet nediferencijuojama. Tačiau kritiniame taške yra dešinioji išvestinė ir dešinioji liestinė, o kitame krašte yra jų kairiarankiai atitikmenys.
Manau, jums nebus sunku atlikti panašius argumentus dėl lanko kosinuso ir jo išvestinės.
Visi pirmiau minėti atvejai, kurių daugelis yra lentelės vediniai, primenu, sekite tiesiai iš išvestiniai apibrėžimai.
Kodėl tyrinėti funkciją naudojant jos išvestinę?
Norėdami geriau suprasti, kaip atrodo šios funkcijos grafikas: kur eina „iš apačios į viršų“, kur „iš viršaus žemyn“, kur pasiekia minimumus ir maksimumus (jei išvis pasiekia). Ne visos funkcijos yra tokios paprastos – daugeliu atvejų mes visai neįsivaizduojame apie konkrečios funkcijos grafiką.
Atėjo laikas pereiti prie prasmingesnių pavyzdžių ir apsvarstyti funkcijos monotoniškumo ir ekstremalumo intervalų paieškos algoritmas:
1 pavyzdys
Raskite funkcijos padidėjimo/sumažėjimo intervalus ir kraštutinumus
![]()
Sprendimas:
1) Pirmas žingsnis yra rasti funkcijos sritis, taip pat atkreipkite dėmesį į lūžio taškus (jei jie yra). Šiuo atveju funkcija yra ištisinė visoje skaičių eilutėje ir šis veiksmas tam tikru mastu yra formalus. Tačiau daugeliu atvejų čia įsiplieskia rimtos aistros, todėl vertinkime pastraipą be panieka.
2) Antrasis algoritmo taškas yra dėl
būtina ekstremumo sąlyga:
Jei taške yra ekstremumas, tada reikšmė arba neegzistuoja.
Supainioti dėl pabaigos? „X modulio“ funkcijos ekstremumas .
Sąlyga būtina, bet neužtenka, ir atvirkščiai ne visada tiesa. Taigi iš lygybės dar neišplaukia, kad funkcija taške pasiekia maksimumą ar minimumą. Klasikinis pavyzdys jau buvo pabrėžtas aukščiau - tai kubinė parabolė ir jos kritinis taškas.
Bet kaip ten bebūtų, būtina ekstremumo sąlyga diktuoja poreikį rasti įtartinus taškus. Norėdami tai padaryti, raskite išvestinę ir išspręskite lygtį:
Pirmojo straipsnio pradžioje apie funkcijų grafikus Aš jums pasakiau, kaip greitai sukurti parabolę naudojant pavyzdį ![]() : „...paimame pirmąją išvestinę ir prilyginame ją nuliui: ...Taigi, mūsų lygties sprendimas: - būtent šioje vietoje yra parabolės viršūnė...“. Dabar, manau, visi supranta, kodėl parabolės viršūnė yra būtent šiame taške =) Apskritai čia reikėtų pradėti nuo panašaus pavyzdžio, bet jis per paprastas (net arbatinukui). Be to, pačioje pamokos pabaigoje yra analogas apie funkcijos išvestinė. Todėl padidinkime laipsnį:
: „...paimame pirmąją išvestinę ir prilyginame ją nuliui: ...Taigi, mūsų lygties sprendimas: - būtent šioje vietoje yra parabolės viršūnė...“. Dabar, manau, visi supranta, kodėl parabolės viršūnė yra būtent šiame taške =) Apskritai čia reikėtų pradėti nuo panašaus pavyzdžio, bet jis per paprastas (net arbatinukui). Be to, pačioje pamokos pabaigoje yra analogas apie funkcijos išvestinė. Todėl padidinkime laipsnį:
2 pavyzdys
Raskite funkcijos monotoniškumo ir ekstremalumo intervalus
Tai pavyzdys, kurį galite išspręsti patys. Visas sprendimas ir apytikslis galutinis problemos pavyzdys pamokos pabaigoje.
Atėjo ilgai lauktas susitikimo su trupmeninėmis-racionaliosiomis funkcijomis momentas:
3 pavyzdys
Išnagrinėkite funkciją naudodami pirmąją išvestinę
Atkreipkite dėmesį, kaip įvairiai tą pačią užduotį galima suformuluoti iš naujo.
Sprendimas:
1) Funkcija taškuose patiria begalinius netolydumus.
2) Mes nustatome kritinius taškus. Raskime pirmąją išvestinę ir prilyginkime ją nuliui: 
Išspręskime lygtį. Trupmena yra lygi nuliui, kai jos skaitiklis yra nulis:
Taigi gauname tris svarbius taškus: ![]()
3) Nubraižome VISUS aptiktus taškus skaičių tiesėje ir intervalo metodas mes apibrėžiame IŠVEDINĖS požymius:
Primenu, kad reikia paimti tam tikrą intervalo tašką ir jame apskaičiuoti išvestinės vertę ![]() ir nustatyti jo ženklą. Pelningiau net neskaičiuoti, o „įvertinti“ žodžiu. Paimkime, pavyzdžiui, tašką, priklausantį intervalui, ir atliksime keitimą:
ir nustatyti jo ženklą. Pelningiau net neskaičiuoti, o „įvertinti“ žodžiu. Paimkime, pavyzdžiui, tašką, priklausantį intervalui, ir atliksime keitimą: ![]() .
. 
Du „pliusai“ ir vienas „minusas“ suteikia „minusą“, vadinasi, išvestinė yra neigiama per visą intervalą.
Veiksmas, kaip suprantate, turi būti atliktas kiekvienam iš šešių intervalų. Beje, atkreipkite dėmesį, kad skaitiklio koeficientas ir vardiklis yra griežtai teigiami bet kuriame bet kurio intervalo taške, o tai labai supaprastina užduotį.
Taigi, išvestinė mums pasakė, kad PATI FUNKCIJA padidėja ![]() ir sumažėja . To paties tipo intervalus patogu sujungti sujungimo piktograma.
ir sumažėja . To paties tipo intervalus patogu sujungti sujungimo piktograma.
Kai funkcija pasiekia maksimumą:
Tuo metu funkcija pasiekia minimumą: ![]()
Pagalvokite, kodėl jums nereikia perskaičiuoti antrosios vertės ;-)
Einant per tašką, išvestinė ženklo nekeičia, todėl funkcija ten NE EKSTREMUMO - ir sumažėjo, ir liko mažėjanti.
! Pakartokime svarbų dalyką: taškai nelaikomi kritiniais – juose yra funkcija neapibrėžtas. Atitinkamai, čia Iš principo negali būti kraštutinumų(net jei išvestinė keičia ženklą).
Atsakymas: funkcija padidėja ![]() ir mažėja Kai pasiekiamas funkcijos maksimumas:
ir mažėja Kai pasiekiamas funkcijos maksimumas: ![]() , o taške – minimumas: .
, o taške – minimumas: .
Žinios apie monotoniškumo intervalus ir ekstremumus, kartu su nustatytais asimptotų jau suteikia labai gerą supratimą apie funkcijų grafiko išvaizdą. Vidutinio pasirengimo žmogus gali žodžiu nustatyti, kad funkcijos grafikas turi du vertikalius asimptotus ir įstrižą asimptotą. Štai mūsų herojus: 
Pabandykite dar kartą susieti tyrimo rezultatus su šios funkcijos grafiku.
Kritiniame taške ekstremumo nėra, bet yra vingio taškas(kas, kaip taisyklė, nutinka panašiais atvejais).
4 pavyzdys
Raskite funkcijos kraštutinumą
5 pavyzdys
Raskite funkcijos monotoniškumo intervalus, maksimumus ir minimumus
...tai beveik kaip kokia „X kube“ šventė šiandien...
Soooo, kas galerijoje už tai pasiūlė išgerti? =)
Kiekviena užduotis turi savo esminius niuansus ir technines subtilybes, kurios pakomentuojamos pamokos pabaigoje.
Funkcijos, visai nebūtina žinoti apie pirmojo ir antrojo darinių buvimą ir suprasti jų fizinę reikšmę. Pirmiausia turite suprasti šiuos dalykus:
- funkcijos ekstremumai padidina arba, atvirkščiai, sumažina funkcijos reikšmę savavališkai mažoje kaimynystėje;
- Ekstremaliame taške neturėtų būti funkcijos nutrūkimų.
O dabar tas pats, tik paprasta kalba. Pažiūrėkite į tušinuko galiuką. Jei rašiklis pastatytas vertikaliai, rašomasis galas į viršų, tada pats rutulio vidurys bus ekstremumas – aukščiausias taškas. Šiuo atveju kalbame apie maksimumą. Dabar, jei pasuksi rašiklį rašymo galu žemyn, tada rutulio viduryje jau bus minimali funkcija. Naudodami čia pateiktą paveikslą, galite įsivaizduoti išvardytas raštinės reikmenų pieštuko manipuliacijas. Taigi funkcijos ekstremumai visada yra kritiniai taškai: jos maksimumas arba minimumas. Gretima grafiko atkarpa gali būti kiek norima aštri arba lygi, tačiau ji turi egzistuoti iš abiejų pusių, tik šiuo atveju taškas yra ekstremumas. Jei grafikas yra tik vienoje pusėje, šis taškas nebus ekstremumas, net jei vienoje pusėje bus įvykdytos ekstremumo sąlygos. Dabar panagrinėkime funkcijos kraštutinumus moksliniu požiūriu. Kad taškas būtų laikomas ekstremumu, būtina ir pakanka, kad:
- pirmoji išvestinė taške buvo lygi nuliui arba neegzistavo;
- pirmasis vedinys šioje vietoje pakeitė savo ženklą.

Sąlyga aiškinama šiek tiek kitaip aukštesnės eilės išvestinių požiūriu: funkcijai, kuri yra diferencijuojama taške, pakanka, kad būtų nelyginės eilės išvestinė, kuri nėra lygi nuliui, o visos žemesnės eilės išvestinės turi egzistuoti. ir būti lygus nuliui. Tai paprasčiausias teoremų aiškinimas iš vadovėlių, tačiau paprastiems žmonėms verta paaiškinti šį klausimą pavyzdžiu. Pagrindas yra įprasta parabolė. Iš karto padarykime rezervaciją: nuliniame taške jis turi minimumą. Šiek tiek matematikos:
- pirmoji išvestinė (X 2) | = 2X, nuliniam taškui 2X = 0;
- antra išvestinė (2X) | = 2, nuliniam taškui 2 = 2.

Šiuo paprastu būdu iliustruojamos sąlygos, lemiančios funkcijos ekstremalumą tiek pirmosios, tiek aukštesnės eilės išvestinėms. Prie to galime pridurti, kad antroji išvestinė yra lygiai tokia pati nelyginės eilės išvestinė, kuri nėra lygi nuliui, kas buvo aptarta aukščiau. Kai kalbama apie dviejų kintamųjų funkcijos kraštutinumus, abiem argumentams turi būti įvykdytos sąlygos. Kai įvyksta apibendrinimas, naudojami daliniai išvestiniai. Tai yra, kad taške būtų ekstremumas, būtina, kad abi pirmosios eilės išvestinės būtų lygios nuliui arba bent vienos iš jų nėra. Siekiant užtikrinti, kad pakaktų ekstremumo buvimo, tiriama išraiška, kuri yra skirtumas tarp funkcijos antros eilės išvestinių sandaugos ir mišrios antros eilės išvestinės kvadrato. Jei ši išraiška didesnė už nulį, tada yra ekstremumas, o jei jis lygus nuliui, klausimas lieka atviras ir reikia atlikti papildomus tyrimus.