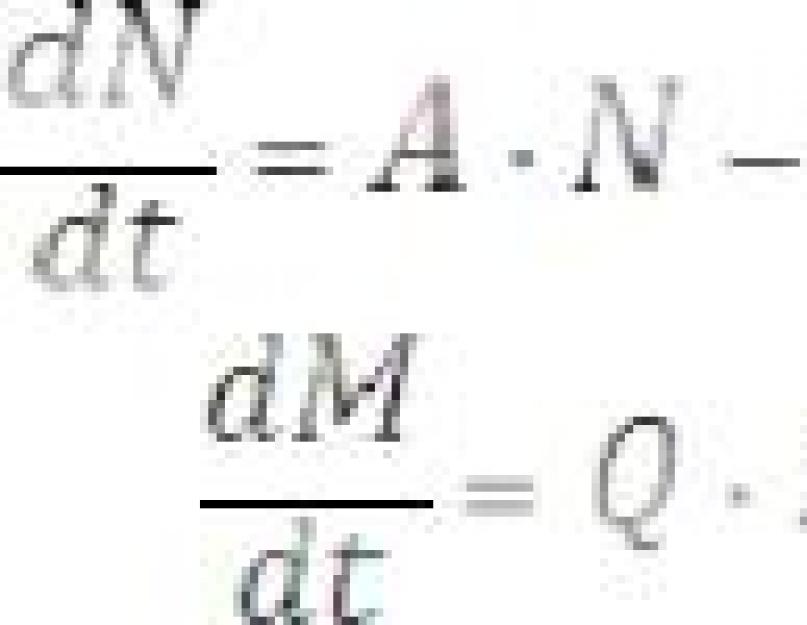Federalinė švietimo agentūra
Valstybinė švietimo įstaiga
aukštasis profesinis išsilavinimas
"Iževsko valstybinis technikos universitetas"
Taikomosios matematikos fakultetas
Katedra "Matematinis procesų ir technologijų modeliavimas"
Kursinis darbas
disciplinoje „Diferencialinės lygtys“
Tema: „Kokybinis plėšrūno-grobio modelio tyrimas“
Iževskas 2010 m
ĮVADAS
1. PARAMETRAI IR PAGRINDINĖ LYGTYBĖ PREDATOR-PREY MODELIO
2.2 Apibendrinti „plėšrūno-grobio“ tipo Voltero modeliai.
3. PRAKTINIS MODELIO PREDATOR-PREY TAIKYMAS
IŠVADA
BIBLIOGRAFIJA
ĮVADAS
Šiuo metu aplinkosaugos problemos yra itin svarbios. Svarbus žingsnis sprendžiant šias problemas yra ekologinių sistemų matematinių modelių sukūrimas.
Vienas iš pagrindinių ekologijos uždavinių dabartiniame etape yra gamtinių sistemų sandaros ir funkcionavimo tyrimas, bendrų dėsningumų paieška. Didelę įtaką ekologijai turėjo matematika, prisidėjusi prie matematinės ekologijos raidos, ypač jos skyriai, tokie kaip diferencialinių lygčių teorija, stabilumo teorija ir optimalaus valdymo teorija.
Vienas pirmųjų darbų matematinės ekologijos srityje buvo A.D. Lotki (1880 - 1949), kuris pirmasis aprašė įvairių populiacijų, kurias sieja plėšrūno ir grobio santykiai, sąveiką. Didelį indėlį į plėšrūno-grobio modelio tyrimą įnešė V. Volterra (1860 - 1940), V.A. Kostitsyn (1883-1963) Šiuo metu populiacijų sąveiką apibūdinančios lygtys vadinamos Lotkos-Volterra lygtimis.
Lotka-Volterra lygtys apibūdina vidutinių verčių dinamiką - populiacijos dydį. Šiuo metu jų pagrindu kuriami bendresni populiacijos sąveikos modeliai, apibūdinami integro-diferencialinėmis lygtimis, tiriami valdomi plėšrūno-grobio modeliai.
Viena iš svarbių matematinės ekologijos problemų yra ekosistemų stabilumo ir šių sistemų valdymo problema. Valdymas gali būti vykdomas su tikslu perkelti sistemą iš vienos stabilios būsenos į kitą, turint tikslą ją panaudoti arba atkurti.
1. PARAMETRAI IR PAGRINDINĖ LYGTYBĖ PREDATOR-PREY MODELIO
Ilgą laiką buvo bandoma matematiškai modeliuoti tiek atskirų biologinių populiacijų, tiek bendrijų, apimančių sąveikaujančias įvairių rūšių populiacijas, dinamiką. Vieną iš pirmųjų izoliuotos populiacijos augimo modelių (2.1) dar 1798 m. pasiūlė Thomas Malthusas:
, (1.1)Šis modelis nustatomas pagal šiuos parametrus:
N – populiacijos dydis;
- skirtumas tarp gimstamumo ir mirtingumo.Integravę šią lygtį gauname:
, (1.2)kur N(0) yra populiacijos dydis šiuo momentu t = 0. Akivaizdu, kad Malthus modelis
> 0 suteikia begalinį skaičiaus augimą, kuris niekada nepastebimas natūraliose populiacijose, kur šį augimą užtikrinantys ištekliai visada yra riboti. Floros ir faunos populiacijų skaičiaus pokyčių negalima apibūdinti paprastu Malthuso dėsniu, daug tarpusavyje susijusių priežasčių turi įtakos augimo dinamikai – visų pirma kiekvienos rūšies dauginimasis yra reguliuojamas ir modifikuojamas taip, kad ši rūšis būtų išsaugota. evoliucija.Šių dėsningumų matematinį apibūdinimą atlieka matematinė ekologija – mokslas apie augalų ir gyvūnų organizmų bei jų kuriamų bendrijų tarpusavio santykius ir su aplinka.
Rimčiausią biologinių bendrijų modelių, apimančių kelias skirtingų rūšių populiacijas, tyrimą atliko italų matematikas Vito Volterra:
, - populiacijos dydis; - natūralaus gyventojų prieaugio (arba mirtingumo) koeficientai; - tarprūšinės sąveikos koeficientai. Priklausomai nuo koeficientų pasirinkimo, modelis apibūdina arba rūšių kovą dėl bendro išteklių, arba plėšrūno-grobio tipo sąveiką, kai viena rūšis yra maistas kitai. Jei kitų autorių darbuose pagrindinis dėmesys buvo skiriamas įvairių modelių konstravimui, tai V. Volterra atliko giluminį sukonstruotų biologinių bendrijų modelių tyrimą. Būtent nuo V. Volterros knygos, daugelio mokslininkų nuomone, prasidėjo šiuolaikinė matematinė ekologija.2. KOKYBINIS ELEMENTINIO MODELIO "PLĖŠONAS- PREY" TYRIMAS
2.1 Plėšrūno ir grobio trofinės sąveikos modelis
Panagrinėkime W. Volterros sukurtą trofinės sąveikos modelį pagal „plėšrūno-grobio“ tipą. Tebūna sistema, susidedanti iš dviejų rūšių, kurių viena valgo kitą.
Apsvarstykite atvejį, kai viena iš rūšių yra plėšrūnas, o kita – grobis, ir manysime, kad plėšrūnas minta tik grobiu. Priimame tokią paprastą hipotezę:
- grobio augimo tempas; - plėšrūnų augimo greitis; - grobio populiacijos dydis; - plėšrūno populiacijos dydis; - aukos natūralaus augimo koeficientas; - plėšrūno suvartoto grobio norma; - plėšrūno mirtingumas nesant grobio; - grobio biomasės „perdirbimo“ į savo biomasę koeficientas.Tada populiacijos dinamika plėšrūno-grobio sistemoje bus aprašyta diferencialinių lygčių sistema (2.1):
(2.1)kur visi koeficientai yra teigiami ir pastovūs.
Modelis turi pusiausvyros sprendimą (2.2):
(2.2)Pagal modelį (2.1) plėšrūnų dalis bendroje gyvūnų masėje išreiškiama formule (2.3):
(2.3)Pusiausvyros būsenos stabilumo mažų perturbacijų atžvilgiu analizė parodė, kad vienaskaitos taškas (2.2) yra „neutraliai“ stabilus („centro“ tipo), t. y. bet kokie nukrypimai nuo pusiausvyros ne mažėja, o perkelia sistema į svyravimo režimą, kurio amplitudė priklauso nuo trikdžių dydžio. Sistemos trajektorijos fazinėje plokštumoje
turėti uždarų kreivių, esančių skirtingais atstumais nuo pusiausvyros taško, formą (1 pav.).Ryžiai. 1 - klasikinės Volteros sistemos "plėšrūnas-grobis" fazė "portretas"
Pirmąją sistemos (2.1) lygtį padalinę iš antrosios, gauname kreivės fazinėje plokštumoje diferencialinę lygtį (2.4).
. (2.4)Integravę šią lygtį, gauname:
(2.5) yra integravimo konstanta, kurNesunku parodyti, kad taško judėjimas išilgai fazės plokštumos vyks tik viena kryptimi. Norėdami tai padaryti, patogu pakeisti funkcijas
ir , perkeliant koordinačių pradžią plokštumoje į nejudantį tašką (2.2) ir įvedant polines koordinates: (2.6)Šiuo atveju sistemos (2.6) reikšmes pakeitę sistema (2.1), turime
Dar 20-aisiais. A. Lotka, o kiek vėliau, nepriklausomai nuo jo, W. Voltaire'as pasiūlė matematinius modelius, apibūdinančius konjuguotus plėšrūno ir grobio skaičiaus svyravimus.
Modelis susideda iš dviejų komponentų:
C – plėšrūnų skaičius; N – aukų skaičius;
Tarkime, nesant plėšrūnų, grobio populiacija augs eksponentiškai: dN/dt = rN. Tačiau grobį plėšrūnai naikina greičiu, kurį lemia plėšrūnų ir grobio susitikimų dažnis, o susidūrimų dažnis didėja didėjant plėšrūnų (C) ir grobio (N) skaičiui. Tikslus sutikto ir sėkmingai suvalgyto grobio skaičius priklausys nuo to, kokiu efektyvumu plėšrūnas suranda ir pagauna grobį, t.y. iš a' – „paieškos efektyvumas“ arba „atakų dažnis“. Taigi „sėkmingų“ plėšrūno ir grobio susitikimų dažnis ir atitinkamai grobio suvartojimo greitis bus lygus a’CN ir apskritai: dN/dt = rN – a’CN (1*).
Trūkstant maisto, atskiri plėšrūno individai numeta svorio, badauja ir miršta. Tarkime, kad nagrinėjamame modelyje plėšrūnų populiacijos dydis nesant maisto dėl bado sumažės eksponentiškai: dC/dt = - qC, kur q – mirtingumas. Mirtis kompensuojama naujų asmenų gimimu tokiu greičiu, kuris, kaip manoma šiame modelyje, priklauso nuo dviejų aplinkybių:
1) maisto suvartojimo norma, a'CN;
2) efektyvumas (f), kuriuo šis maistas patenka į plėšrūno palikuonis.
Taigi plėšrūno gimstamumas lygus fa’CN ir apskritai: dC/dt = fa’CN – qC (2*). 1* ir 2* lygtys sudaro Lotka-Voltaire modelį. Galima ištirti šio modelio savybes, sukonstruoti pastovų populiacijos dydį atitinkančias linijines izoklinas, tokių izoklinų pagalba nustatoma sąveikaujančių plėšrūnų ir grobio populiacijų elgsena.
Grobio populiacijos atveju: dN/dt = 0, rN = a'CN arba C = r/a'. Nes r ir a' = const, aukos izoklinija bus ta linija, kuriai C reikšmė yra pastovi:
Esant mažam plėšrūnų tankiui (C), grobio (N) skaičius didėja, priešingai – mažėja.
Panašiai ir plėšrūnams (2 lygtis*), kurių dC/dt = 0, fa’CN = qC arba N = q/fa’, t.y. plėšrūno izoklina bus linija, išilgai kurios N yra pastovus: Esant dideliam grobio tankiui, plėšrūnų populiacija didėja, o esant mažam – mažėja.
Jų skaičius neribotai svyruoja. Kai grobio skaičius yra didelis, plėšrūnų skaičius didėja, o tai padidina plėšrūnų spaudimą grobio populiacijai ir dėl to mažėja jų skaičius. Dėl šio sumažėjimo savo ruožtu ribojamas plėšrūnų kiekis maiste ir sumažėja jų skaičius, dėl to susilpnėja plėšrūnų spaudimas ir didėja grobio skaičius, o tai vėl lemia plėšrūnų populiacijos padidėjimą. ir kt.
Populiacijos atlieka tą patį svyravimų ciklą neribotą laiką, kol koks nors išorinis poveikis nepakeičia jų skaičių, o po to populiacijos atlieka naujus neribotų svyravimų ciklus. Tiesą sakant, aplinka nuolat keičiasi, o populiacijų skaičius nuolat pereis į naują lygį. Kad populiacijos svyravimų ciklai būtų reguliarūs, jie turi būti stabilūs: jei išorinė įtaka pakeičia populiacijų lygį, tada jos turi krypti į pradinį ciklą. Tokie ciklai vadinami stabiliais, ribiniais ciklais.
Lotkos-Voltaire modelis leidžia parodyti pagrindinę plėšrūno ir grobio santykio tendenciją, kuri išreiškiama grobio populiacijos gausos svyravimais, kuriuos lydi plėšrūnų populiacijos gausos svyravimai. Pagrindinis tokių svyravimų mechanizmas yra laiko delsimas, būdingas būsenos sekai nuo didelio grobio iki didelio plėšrūnų skaičiaus, tada iki mažo grobio ir mažo plėšrūnų skaičiaus iki didelio grobio skaičiaus. , ir taip toliau.
5) PLĖŠRUSIŲ IR grobio POPULIACINĖS STRATEGIJOS
Santykiai „plėšrūnas – grobis“ reiškia ryšius, vykstančius medžiagos ir energijos perdavimo procese iš fitofagų į zoofagus arba iš žemesnės eilės plėšrūnų į aukštesnės eilės plėšrūnus. Autorius šių santykių pobūdis išskiria tris plėšrūnų variantus:
a) kolekcininkai. Predator renka mažas, gana daug judančių aukų. Šis plėšrumo variantas būdingas daugeliui paukščių rūšių (ploteriams, kikiliams, dygioms ir kt.), kurie energiją eikvoja tik grobio paieškai;
b) tikri plėšrūnai. Plėšrūnas persekioja ir žudo grobį;
in) ganyklos. Šie plėšrūnai grobį naudoja pakartotinai, pavyzdžiui, arklius ar arklius.
Plėšrūnų maisto gavimo strategija siekiama užtikrinti mitybos energinį efektyvumą: energijos suvartojimas maistui gauti turi būti mažesnis nei energija, gaunama jį asimiliuojant.
Tikri plėšrūnai yra skirstomi į
„javapjūtės“, mintančios gausiais ištekliais (n, planktoninės žuvys ir net baliniai banginiai), ir „medžiotojai“, kurie gauna mažiau maisto. Savo ruožtu
„medžiotojai“ skirstomi į „pasalą“, tykančius grobio (pavyzdžiui, lydekos, vanago, katės, mantija), „ieškotojus“ (vabzdžiaėdžius paukščius) ir „persekiotojus“. Pastarajai grupei maisto paieška nereikalauja daug energijos, tačiau jos reikia nemažai, kad suvaldytų grobį (liūtus savanose). Tačiau kai kurie plėšrūnai gali derinti skirtingų medžioklės variantų strategijos elementus.
Kaip ir „fitofago ir augalo“ santykio atveju, gamtoje nepastebima situacija, kai visas aukas suvalgys plėšrūnai, o tai galiausiai lems jų mirtį. ekologinė pusiausvyra tarp plėšrūnų ir grobio palaikoma specialiais mechanizmais kurie sumažina visiško aukų sunaikinimo riziką. Taip, aukos gali:
Bėk nuo plėšrūno. Tokiu atveju dėl adaptacijų padidėja ir aukų, ir plėšrūnų mobilumas, o tai ypač būdinga stepių gyvūnams, kurie neturi kur pasislėpti nuo persekiotojų;
Įsigykite apsauginę spalvą („apsimesti“ lapais ar mazgais) arba, priešingai, ryškią spalvą N .: raudona, įspėjanti plėšrūną apie kartaus skonio. Gerai žinoma, kad kiškio spalva keičiasi skirtingu metų laiku, todėl vasarą jis gali maskuotis žolėje, o žiemą - balto sniego fone. Adaptyvus spalvos pokytis gali atsirasti skirtingose ontogenezės stadijose: ruonių jaunikliai yra balti (sniego spalva), o suaugusieji yra juodi (uolėtos pakrantės spalva);
Pasiskirstyti grupėmis, todėl jų paieška ir žvejyba sunaudoja daug energijos;
Slėpti prieglaudose;
Pereikite prie aktyvios gynybos priemonių (žolėdžiai su ragais, dygliuotos žuvys), kartais sąnarių (muskuso jaučiai gali imtis „visapusės gynybos“ nuo vilkų ir kt.).
Savo ruožtu plėšrūnai lavina ne tik gebėjimą greitai persekioti aukas, bet ir uoslę, kuri leidžia pagal kvapą nustatyti aukos vietą. Daugelis plėšrūnų rūšių drasko savo aukų (lapių, vilkų) skyles.
Tuo pačiu metu jie patys daro viską, kad neatskleistų savo buvimo. Tai paaiškina mažų kačių švarą, kurios daug laiko praleidžia tualete ir užkasa ekskrementus, kad pašalintų kvapą. Plėšrūnai dėvi „kamufliažinius drabužius“ (lydekų ir ešerių juostelės, dėl kurių jie mažiau matomi makrofitų tankmėje, tigrų dryžiai ir kt.).
Visiška apsauga nuo visų grobio gyvūnų populiacijų individų taip pat neįvyksta, nes tai sukeltų ne tik badaujančių plėšrūnų mirtį, bet galiausiai ir grobio populiacijų katastrofą. Tuo pačiu metu, nesant arba mažėjant plėšrūnų populiacijos tankiui, grobio populiacijos genofondas blogėja (lieka sergantys ir seni gyvūnai), o dėl staigios jų skaičiaus padidėjimo kenkia maisto bazė.
Dėl šios priežasties grobio ir plėšrūnų populiacijų skaičiaus priklausomybės efektas – grobio populiacijos pulsavimas, po kurio su tam tikru uždelsimu ima pulsuoti plėšrūnų populiacijos skaičius („Lotka-Volterra efektas“). ) – stebimas retai.
Nustatytas gana stabilus plėšrūnų ir grobio biomasės santykis. Taigi, R. Ricklefsas cituoja duomenis, kad plėšrūnų ir grobio biomasės santykis svyruoja nuo 1:150 iki 1:300. Įvairiose JAV vidutinio klimato juostos ekosistemose vienam vilkui tenka 300 mažų baltauodegių elnių (sveria 60 kg), 100 didelių briedžių elnių (sveria 300 kg) arba 30 briedžių (svoris 350). Tas pats modelis buvo rastas savanose.
Intensyviai eksploatuodami fitofagų populiacijas, žmonės dažnai iš ekosistemų išskiria plėšrūnus (pavyzdžiui, JK yra stirnų ir elnių, bet vilkų nėra, dirbtinuose rezervuaruose, kur veisiasi karpiai ir kitos tvenkinių žuvys, lydekų nėra). Šiuo atveju plėšrūno vaidmenį atlieka pats žmogus, pašalindamas dalį fitofagų populiacijos individų.
Ypatingas plėšrūnų variantas stebimas augaluose ir grybuose. Augalų karalystėje yra apie 500 rūšių, kurios proteolitinių fermentų pagalba gali gaudyti vabzdžius ir iš dalies juos suvirškinti. Plėšrieji grybai sudaro gaudymo įtaisus mažų ovalių arba sferinių galvų pavidalu, esančiais ant trumpų grybienos šakelių. Tačiau labiausiai paplitęs spąstų tipas yra lipnūs trimačiai tinklai, susidedantys iš daugybės žiedų, susidarančių išsišakojus hifams. Plėšrūs grybai gali sugauti gana didelius gyvūnus, tokius kaip apvaliosios kirmėlės. Kirminui įsipainiojus į hifus, jie auga gyvūno kūno viduje ir greitai jį užpildo.
1.Pastovus ir palankus temperatūros ir drėgmės lygis.
2. Maisto gausa.
3. Apsauga nuo nepalankių veiksnių.
4. Agresyvi cheminė aplinkos sudėtis (virškinimo sultys).
1. Dviejų buveinių buvimas: pirmosios eilės aplinka – šeimininkas, antros eilės aplinka – išorinė aplinka.
PA88 sistema, kuri pagal jos struktūrinę formulę vienu metu numato daugiau nei 100 medžiagos farmakologinių poveikių ir veikimo mechanizmų tikimybę. Šio metodo taikymo atrankos planavimui efektyvumas yra apie 800%, o kompiuterinio prognozavimo tikslumas yra 300% didesnis nei ekspertų.
Taigi, vienas iš konstruktyvių įrankių naujų žinių ir sprendimų medicinoje gavimui yra matematinio modeliavimo metodas. Medicinos matematizavimo procesas yra dažna mokslo žinių skverbimosi apraiška, didinanti medicininio ir prevencinio darbo efektyvumą.
4. Matematinis modelis "plėšrūnai-grobis"
Pirmą kartą biologijoje matematinį antagonistinių gyvūnų rūšių skaičiaus periodinio kitimo modelį pasiūlė italų matematikas V. Volterra ir jo bendradarbiai. Volteros pasiūlytas modelis buvo 1924 metais A. Lotkos knygoje „Fizinės biologijos elementai“ išdėstytos idėjos plėtojimas. Todėl šis klasikinis matematinis modelis žinomas kaip „Lotka-Volterra“ modelis.
Nors antagonistiniai rūšių ryšiai yra sudėtingesni nei modelio, jie vis dėlto yra geras edukacinis modelis, pagal kurį galima išmokti pagrindinių matematinio modeliavimo idėjų.
Taigi, užduotis: tam tikroje ekologiškai uždaroje teritorijoje gyvena dviejų rūšių gyvūnai (pavyzdžiui, lūšys ir kiškiai). Kiškiai (grobis) minta augaliniu maistu, kurio visada yra pakankamais kiekiais (šiame modelyje neatsižvelgiama į ribotus augalinio maisto išteklius). Lūšys (plėšrūnai) gali valgyti tik kiškius. Būtina nustatyti, kaip tokioje ekologinėje sistemoje laikui bėgant keisis grobio ir plėšrūnų skaičius. Jei grobio populiacija didėja, padidėja plėšrūnų ir grobio susidūrimo tikimybė, todėl, praėjus tam tikram laikui, plėšrūnų populiacija auga. Šis gana paprastas modelis gana adekvačiai apibūdina realių plėšrūnų populiacijų ir grobio sąveiką gamtoje.
Dabar pereikime prie diferencialinių lygčių sudarymas. Ob-
grobio skaičių žymime per N, o plėšrūnų skaičių – per M. Skaičiai N ir M yra laiko t funkcijos. Savo modelyje atsižvelgiame į šiuos veiksnius:
a) natūralus aukų dauginimasis; b) natūrali aukų mirtis;
c) aukų naikinimas jas valgant plėšrūnams; d) natūralus plėšrūnų išnykimas;
e) plėšrūnų skaičiaus padidėjimas dėl dauginimosi su maistu.
Kadangi kalbame apie matematinį modelį, užduotis yra gauti lygtis, kurios apimtų visus numatytus veiksnius ir kurios apibūdintų dinamiką, tai yra plėšrūnų ir grobio skaičiaus kitimą laikui bėgant.
Tegul kurį laiką t grobio ir plėšrūnų skaičius pasikeičia ∆N ir ∆M. Aukų skaičiaus pokytis ∆N laikui bėgant ∆t visų pirma nustatomas dėl padidėjimo dėl natūralaus dauginimosi (kuris yra proporcingas esančių aukų skaičiui):
kur B yra proporcingumo koeficientas, apibūdinantis natūralaus aukų išnykimo greitį.
Lygties, apibūdinančios grobio skaičiaus sumažėjimą dėl plėšrūnų suėdimo, išvedimo esmė yra mintis, kad kuo dažniau jie susitinka, tuo greičiau mažėja grobio skaičius. Taip pat aišku, kad plėšrūnų ir grobio susitikimų dažnis yra proporcingas ir grobio, ir plėšrūnų skaičiui, tada
Padalinę (4) lygties kairę ir dešinę puses iš ∆t ir pereidami prie ribos ties ∆t→0 , gauname pirmos eilės diferencialinę lygtį:
Norėdami išspręsti šią lygtį, turite žinoti, kaip laikui bėgant kinta plėšrūnų skaičius (M). Plėšrūnų skaičiaus pokytį (∆M ) lemia padidėjimas dėl natūralaus dauginimosi esant pakankamai maisto (M 1 = Q∙N∙M∙∆t ) ir sumažėjimas dėl natūralaus plėšrūnų išnykimo ( M 2 = - P∙M∙∆ t):
M = Q∙N∙M∙∆t – P∙M∙∆t |
Iš (6) lygties galima gauti diferencialinę lygtį:
Diferencialinės lygtys (5) ir (7) atspindi matematinį modelį „plėšrūnai-grobis“. Pakanka nustatyti koeficiento reikšmes

Problemai išspręsti gali būti naudojami komponentai A, B, C, Q, P ir matematinis modelis.
Matematinio modelio patikrinimas ir taisymas. Šioje laboratorijoje -
Šiame darbe, be išsamiausio matematinio modelio skaičiavimo (5 ir 7 lygtys), siūloma ištirti paprastesnius, kuriuose į kažką neatsižvelgiama.
Įvertinus penkis matematinio modelio sudėtingumo lygius, galima „pajusti“ modelio tikrinimo ir taisymo etapą.
1 lygis - modelis atsižvelgia į "aukas" tik į jų natūralų dauginimąsi, "plėšrūnų" nėra;
2 lygis – modelyje atsižvelgiama į natūralų „aukų“ išnykimą, „plėšrūnų“ nėra;
3 lygis – modelis atsižvelgia į „aukų“ natūralų dauginimąsi
ir išnykimas, „plėšrūnų“ nėra;
4 lygis – modelis atsižvelgia į „aukų“ natūralų dauginimąsi
ir išnykimas, taip pat „plėšrūnų“ valgymas, tačiau „plėšrūnų“ skaičius nesikeičia;
5 lygis – modelis atsižvelgia į visus aptartus veiksnius.
Taigi, turime tokią diferencialinių lygčių sistemą:
čia M yra "plėšrūnų" skaičius; N yra „aukų“ skaičius;
t yra dabartinis laikas;
A – „aukų“ dauginimosi greitis; C – „plėšrūno ir grobio“ susitikimų dažnis; B – „aukų“ išnykimo rodiklis;
Q - "plėšrūnų" reprodukcija;
P – „plėšrūnų“ išnykimas.
1 lygis: M = 0, B = 0; 2 lygis: M = 0, A = 0; 3 lygis: M = 0; 4 lygis: Q = 0, P = 0;
5 lygis: visa lygčių sistema.
Pakeitę koeficientų reikšmes į kiekvieną lygį, gausime skirtingus sprendimus, pavyzdžiui:
3 lygiui koeficiento reikšmė M=0, tada

išspręsdami gautą lygtį
Panašiai ir 1 ir 2 lygiuose. Kalbant apie 4 ir 5 lygius, čia reikia išspręsti lygčių sistemą Runge-Kutta metodu. Rezultate gauname šių lygių matematinių modelių sprendimą.
II. MOKINIŲ DARBAS PRAKTINĖS PAMOKOS METU
1 pratimas. Pamokos teorinės medžiagos įsisavinimo žodinės kalbos kontrolė ir korekcija. Išduodamas leidimas praktikuotis.
2 užduotis . Laboratorinių darbų atlikimas, gautų rezultatų aptarimas, suvestinės sudarymas.
Darbo užbaigimas
1. Iš kompiuterio darbalaukio iškvieskite programą „Lab. Nr. 6“, kairiuoju pelės klavišu dukart spustelėdami atitinkamą etiketę.
2. Dukart spustelėkite kairįjį pelės mygtuką ant etiketės "PREDATOR".
3. Pasirinkite nuorodą „PRED“ ir pakartokite programos iškvietimą kairiuoju pelės mygtuku (du kartus spustelėdami).
4. Po pavadinimo spragtelėkite "ENTER".
5. Modeliavimas pradėkite nuo 1 lygis.
6. Įveskite metus, nuo kurių bus atliekama modelio analizė: pavyzdžiui, 2000 m
7. Pasirinkite laiko intervalus, pavyzdžiui, per 40 metų, po 1 metų (tada po 4 metų).
2 lygis: B = 0,05; N0 = 200;
3 lygis: A = 0,02; B = 0,05; N = 200;
4 lygis: A = 0,01; B = 0,002; C = 0,01; N0 = 200; M = 40; 5 lygis: A = 1; B = 0,5; C = 0,02; Q = 0,002; P = 0,3; N0 = 200;
9. Parengti darbo ataskaitą raštu, kurioje turi būti lygtys, grafikai, modelio charakteristikų skaičiavimo rezultatai, išvados apie atliktą darbą.
3 užduotis. Galutinio žinių lygio kontrolė:
a) žodinė ataskaita už atliktus laboratorinius darbus; b) situacinių problemų sprendimas; c) kompiuterinis testavimas.
Užduotis 4. Užduotis kitai pamokai: pamokos skyrius ir tema, abstrakčių pranešimų temų derinimas (pranešimo dydis 2-3 puslapiai, laikas 5-7 min.).
Plėšrūnai gali valgyti žolėdžius, taip pat silpnus plėšrūnus. Plėšrūnai turi platų maisto asortimentą, lengvai pereina nuo vieno grobio prie kito, lengviau pasiekiami. Plėšrūnai dažnai puola silpną grobį. Išlaikoma ekologinė pusiausvyra tarp grobio-plėšrūnų populiacijų.[ ...]
Jei pusiausvyra nestabili (nėra ribinių ciklų) arba išorinis ciklas nestabilus, tai abiejų rūšių skaičius, patiriantis stiprius svyravimus, palieka pusiausvyros apylinkes. Be to, greita degeneracija (pirmoje situacijoje) įvyksta mažai prisitaikius plėšrūnui, t.y. su dideliu mirtingumu (palyginti su aukos reprodukcijos greičiu). Tai reiškia, kad visais atžvilgiais silpnas plėšrūnas neprisideda prie sistemos stabilizavimo ir išmiršta pats.[ ...]
Plėšrūnų spaudimas ypač stiprus, kai plėšrūno ir grobio koevoliucijoje pusiausvyra pasislenka plėšrūno link ir grobio arealas siaurėja. Konkurencinė kova yra glaudžiai susijusi su maisto išteklių trūkumu, tai gali būti ir tiesioginė, pavyzdžiui, plėšrūnų kova dėl erdvės, kaip ištekliaus, tačiau dažniausiai tai yra tiesiog rūšies, kuri neturi pakankamai maisto, išstūmimas. teritoriją suteikia rūšis, kuriai pakanka tokio pat maisto kiekio. Tai yra tarprūšinė konkurencija.[ ...]
 |
Galiausiai (2.7) modeliu aprašytoje sistemoje „plėšrūnas-grobis“ difuzijos nestabilumo atsiradimas (esant vietiniam pusiausvyros stabilumui) yra įmanomas tik tuo atveju, jei natūralus plėšrūno mirtingumas didėja didėjant jo populiacijai greičiau nei tiesinė funkcija. trofinė funkcija skiriasi nuo Volteros arba kai grobio populiacija yra Ollie tipo populiacija.[ ...]
Teoriškai modeliuose „vienas plėšrūnas – du grobis“ lygiavertis plėšrūnas (pirenybės neteikimas vienam ar kitam grobio tipui) gali paveikti konkurencinį grobio rūšių sambūvį tik tose vietose, kur jau yra galimai stabili pusiausvyra. Įvairovė gali didėti tik tokiomis sąlygomis, kai mažiau konkurencingos rūšys turi didesnį populiacijos augimo tempą nei dominuojančios rūšys. Tai leidžia suprasti situaciją, kai net ir ganymas lemia augalų rūšių įvairovės didėjimą, kai didesnis skaičius sparčiai dauginimuisi atrinktų rūšių sugyvena su rūšimis, kurių evoliucija siekiama didinti konkurencingumą.[...]
Lygiai taip pat grobio pasirinkimas, priklausomai nuo jo tankio, gali lemti stabilią pusiausvyrą dviejų konkuruojančių grobio tipų teoriniuose modeliuose, kur anksčiau nebuvo pusiausvyros. Kad tai padarytų, plėšrūnas turi gebėti funkciškai ir skaičiais reaguoti į grobio tankio pokyčius; tačiau gali būti, kad perėjimas (neproporcingai dažni išpuoliai prieš gausiausią auką) šiuo atveju bus svarbesnis. Iš tiesų, buvo nustatyta, kad perjungimas turi stabilizuojantį poveikį sistemose „vienas plėšrūnas – n grobio“ ir yra vienintelis mechanizmas, galintis stabilizuoti sąveiką, kai grobio nišos visiškai persidengia. Šį vaidmenį gali atlikti nespecializuoti plėšrūnai. Labiau specializuotų plėšrūnų pirmenybė dominuojančiam konkurentui veikia taip pat, kaip plėšrūnų pasikeitimas, ir gali stabilizuoti teorinę sąveiką modeliuose, kuriuose anksčiau nebuvo pusiausvyros tarp grobio rūšių, su sąlyga, kad jų nišos yra tam tikru mastu atskirtos. .]
Taip pat bendruomenė nėra stabilizuota ir plėšrūnas yra „visais atžvilgiais stiprus“, t.y. gerai prisitaikę prie tam tikro grobio ir su mažu santykiniu mirtingumu. Tokiu atveju sistema turi nestabilų ribinį ciklą ir, nepaisant pusiausvyros padėties stabilumo, išsigimsta atsitiktinėje aplinkoje (plėšrūnas suvalgo grobį ir dėl to miršta). Ši situacija atitinka lėtą degeneraciją.[ ...]
Taigi, plėšrūnui gerai prisitaikant prie stabilios pusiausvyros, gali atsirasti nestabilūs ir stabilūs ciklai, t.y. Priklausomai nuo pradinių sąlygų, „plėšrūno-grobio“ sistema arba linkusi į pusiausvyrą, arba, svyruodama, ją palieka, arba šalia pusiausvyros nusistovėję abiejų rūšių skaičiaus svyravimai yra stabilūs.[ ...]
Plėšrūnams priskiriami organizmai minta kitais organizmais, naikindami savo grobį. Taigi tarp gyvų organizmų reikėtų išskirti dar vieną klasifikavimo sistemą – „plėšrūnus“ ir „aukas“. Tokių organizmų ryšiai vystėsi per visą gyvybės evoliuciją mūsų planetoje. Plėšrieji organizmai veikia kaip natūralūs grobio organizmų skaičiaus reguliatoriai. Padidėjus „plėšrūnų“ skaičiui, mažėja „grobio“, o tai savo ruožtu sumažina maisto („grobio“) pasiūlą „plėšrūnams“, o tai paprastai lemia jų skaičiaus mažėjimą. „grobio“ ir tt Taigi, biocenozėje yra nuolatiniai plėšrūnų ir grobio skaičiaus svyravimai, paprastai tam tikrą laiką nusistovi tam tikra pusiausvyra gana stabiliomis aplinkos sąlygomis.[ ... ]
Taip galiausiai pasiekiama ekologinė pusiausvyra tarp plėšrūnų ir grobio populiacijų.[ ...]
Trečiojo tipo trofinei funkcijai pusiausvyros būsena bus stabili, jei kur N yra funkcijos vingio taškas (žr. 2 pav., c). Tai išplaukia iš to, kad trofinė funkcija intervale yra įgaubta ir dėl to didėja santykinė plėšrūno suvartoto grobio dalis.[ ...]
Tegu Гг = -Г, t.y. yra „plėšrūno-grobio“ tipo bendruomenė. Šiuo atveju (7.4) išraiškos pirmasis narys yra lygus nuliui, o norint įvykdyti stabilumo sąlygą pusiausvyros būsenos N tikimybės atžvilgiu, reikia, kad ir antrasis narys nebūtų teigiamas. ...]
Taigi nagrinėjamai plėšrūno-grobio tipo bendruomenei galime daryti išvadą, kad apskritai teigiama pusiausvyra yra asimptotiškai stabili, t. y. bet kokiems pradiniams duomenims, jei N >0.[ ...]
Taigi, vienalytėje aplinkoje, kurioje nėra prieglaudų daugintis, plėšrūnas anksčiau ar vėliau sunaikina grobio populiaciją, o paskui pats išmiršta. Gyvybės bangos“ (plėšrūno ir grobio skaičiaus pokyčiai) seka viena kitą su nuolatiniu fazės poslinkiu, ir vidutiniškai tiek plėšrūnų, tiek grobio skaičius išlieka maždaug tame pačiame lygyje. Periodo trukmė priklauso nuo abiejų rūšių augimo tempų ir nuo pradinių parametrų. Grobuonių populiacijai plėšrūno įtaka yra teigiama, nes per didelis jo dauginimasis lemtų jo skaičiaus žlugimą. Savo ruožtu visi mechanizmai, neleidžiantys visiškai išnaikinti grobio, prisideda prie plėšrūno maisto bazės išsaugojimo.[ ...]
Kiti pakeitimai gali atsirasti dėl plėšrūno elgesio. Grobio individų skaičius, kurį plėšrūnas gali suvalgyti tam tikru metu, turi savo ribą. Plėšrūno prisotinimo poveikis artėjant prie šios ribos parodytas lentelėje. 2-4, B. 5 ir 6 lygtimis aprašytos sąveikos gali turėti stabilius pusiausvyros taškus arba turėti ciklinius svyravimus. Tačiau tokie ciklai skiriasi nuo tų, kurie atsispindi Lotkos-Volterra lygtyse 1 ir 2. 5 ir 6 lygtimis perteikti ciklai gali turėti pastovią amplitudę ir vidutinį tankį tol, kol terpė yra pastovi; įvykus pažeidimui, jie gali grįžti prie ankstesnių amplitudių ir vidutinių tankių. Tokie ciklai, kurie atkuriami po pažeidimų, vadinami stabiliais ribiniais ciklais. Kiškio ir lūšies sąveiką galima laikyti stabiliu ribiniu ciklu, tačiau tai nėra Lotkos-Volteros ciklas.[ ...]
Panagrinėkime difuzijos nestabilumo atsiradimą sistemoje „plėšrūnas-grobis“, bet pirmiausia išrašysime sąlygas, užtikrinančias difuzijos nestabilumo atsiradimą sistemoje (1.1), kai n = 2. Aišku, kad pusiausvyra (N , W) yra vietinis (t. y. [ .. .]
Pereikime prie atvejų, susijusių su ilgalaikiu plėšrūno ir grobio sambūviu, aiškinimo. Akivaizdu, kad nesant ribinių ciklų, stabili pusiausvyra atitiks populiacijos svyravimus atsitiktinėje aplinkoje, o jų amplitudė bus proporcinga trikdžių sklaidai. Toks reiškinys įvyks, jei plėšrūnas turės didelį santykinį mirtingumą ir tuo pačiu aukštą prisitaikymo prie konkretaus grobio laipsnį.[ ...]
Dabar panagrinėkime, kaip keičiasi sistemos dinamika didėjant plėšrūno tinkamumui, t.y. mažėjant b nuo 1 iki 0. Jei tinkamumas pakankamai žemas, tai nėra ribinių ciklų, o pusiausvyra nestabili. Augant tinkamumui šalia šios pusiausvyros, galimas stabilus ciklas, o vėliau ir išorinis nestabilus ciklas. Priklausomai nuo pradinių sąlygų (plėšrūno ir grobio biomasės santykio), sistema gali arba prarasti stabilumą, t.y. palikite pusiausvyros apylinkes arba laikui bėgant joje nusistovės stabilūs svyravimai. Tolesnis kūno rengybos augimas neleidžia svyruoti sistemos elgesio. Tačiau kai b [...]
Neigiamo (stabilizuojančio) grįžtamojo ryšio pavyzdys yra plėšrūno ir grobio ryšys arba vandenyno karbonatų sistemos funkcionavimas (CO2 tirpalas vandenyje: CO2 + H2O -> H2CO3). Paprastai vandenyno vandenyje ištirpusio anglies dioksido kiekis yra dalinėje pusiausvyroje su anglies dioksido koncentracija atmosferoje. Vietinis anglies dioksido padidėjimas atmosferoje po ugnikalnių išsiveržimų sukelia fotosintezės intensyvėjimą ir jo absorbciją vandenyno karbonatų sistemoje. Mažėjant anglies dioksido lygiui atmosferoje, vandenyno karbonatų sistema į atmosferą išskiria CO2. Todėl anglies dvideginio koncentracija atmosferoje yra gana stabili.[ ...]
[ ...]
Kaip pažymi R. Ricklefs (1979), yra veiksnių, kurie prisideda prie santykių stabilizavimo „plėšrūno ir grobio“ sistemoje: plėšrūno neefektyvumas, alternatyvių maisto išteklių buvimas plėšrūne, sumažėjęs uždelsimas. plėšrūno reakcija, taip pat aplinkos apribojimai, kuriuos išorinė aplinka nustato vienai ar kelioms skirtingoms populiacijoms. Sąveika tarp plėšrūnų ir grobio populiacijų yra labai įvairi ir sudėtinga. Taigi, jei plėšrūnai yra pakankamai efektyvūs, jie gali reguliuoti grobio populiacijos tankį, išlaikydami jį žemiau aplinkos pajėgumo. Dėl savo įtakos grobio populiacijoms plėšrūnai daro įtaką įvairių grobio savybių evoliucijai, o tai galiausiai lemia ekologinę pusiausvyrą tarp plėšrūnų ir grobio populiacijų.[...]
Jei tenkinama viena iš sąlygų: 0 1/2. Jei 6 > 1 (kA [ ...]
Biotos ir aplinkos stabilumas priklauso tik nuo augalų – autotrofų ir žolėdžių heterotrofinių organizmų sąveikos. Bet kokio dydžio plėšrūnai negali sutrikdyti bendruomenės ekologinės pusiausvyros, nes natūraliomis sąlygomis jie negali padidinti savo skaičiaus su pastoviu grobio skaičiumi. Plėšrūnai ne tik patys turi judėti, bet gali maitintis tik judančiais gyvūnais.[ ...]
Jokia kita žuvis nėra taip plačiai paplitusi kaip lydekos. Keliose žvejybos vietose stovinčiame ar tekančiame vandenyse lydekos nespaudžia išlaikyti balanso tarp grobio ir plėšrūno. Pasaulyje lydekos itin gausiai atstovaujamos. Jie sugaunami visame šiauriniame) pusrutulyje nuo JAV ir Kanados Šiaurės Amerikoje, per Europą iki Šiaurės Azijos.[ ...]
Čia iškyla dar viena stabilaus sambūvio galimybė siaurame santykinai aukšto prisitaikymo diapazone. Pereinant į nestabilų režimą su labai „geru“ plėšrūnu, gali susidaryti stabilus išorinis ribinis ciklas, kuriame biomasės išsisklaidymo pusiausvyra yra jos patekimas į sistemą (didelis grobio produktyvumas). Tada susidaro kurioziška situacija, kai labiausiai tikėtinos yra dvi būdingos atsitiktinių svyravimų amplitudės reikšmės. Kai kurie įvyksta beveik pusiausvyroje, kiti - netoli ribinio ciklo, ir galimi dažnesni ar retesni perėjimai tarp šių režimų.[ ...]
Hipotetinės populiacijos, kurios elgiasi pagal vektorius Fig. 10,11 A, parodyta pav. 10.11,-B grafiko, parodančio plėšrūno ir grobio skaičiaus santykio dinamiką, pagalba ir pav. 10.11.5 plėšrūnų ir grobio skaičiaus dinamikos laikui bėgant grafikas. Grobio populiacijoje, kai ji pereina iš mažo tankio pusiausvyros į didelio tankio pusiausvyrą ir grįžta atgal, įvyksta skaičių „blyksnis“. Ir šis protrūkis nėra vienodai ryškaus aplinkos pasikeitimo rezultatas. Priešingai, šį skaičių pokytį sukelia pats poveikis (su žemu „triukšmo“ lygiu aplinkoje) ir visų pirma jis atspindi kelių pusiausvyros būsenų buvimą. Panašūs samprotavimai gali būti naudojami paaiškinant sudėtingesnius natūralių populiacijų populiacijos dinamikos atvejus.[ ...]
Svarbiausia ekosistemos savybė yra jos stabilumas, mainų ir joje vykstančių procesų pusiausvyra. Populiacijų ar ekosistemų gebėjimas išlaikyti stabilią dinaminę pusiausvyrą kintančiomis aplinkos sąlygomis vadinamas homeostaze (homoios – tas pats, panašus; stasis – būsena). Homeostazė remiasi grįžtamojo ryšio principu. Norint išlaikyti pusiausvyrą gamtoje, nereikia jokios išorinės kontrolės. Homeostazės pavyzdys yra „plėšrūno-grobio“ posistemė, kurioje reguliuojamas plėšrūnų ir grobio populiacijų tankis.[ ...]
Natūrali ekosistema (biogeocenozė) funkcionuoja stabiliai, nuolat sąveikaujant jos elementams, cirkuliuojant medžiagoms, perduodant cheminę, energetinę, genetinę ir kitą energiją bei informaciją grandininiais kanalais. Pagal pusiausvyros principą bet kuri natūrali sistema, turinti energijos ir informacijos srautą, yra linkusi sukurti stabilią būseną. Tuo pačiu metu ekosistemų stabilumas užtikrinamas automatiškai dėl grįžtamojo ryšio mechanizmo. Grįžtamasis ryšys susideda iš duomenų, gautų iš valdomų ekosistemos komponentų, panaudojimo proceso valdymo komponentams koreguoti. Aukščiau šiame kontekste aptartą santykį „plėšrūnas“ – „grobis“ galima apibūdinti kiek plačiau; taigi vandens ekosistemoje plėšriosios žuvys (lydekos tvenkinyje) minta kitų rūšių plėšriomis žuvimis (karpiais); jei karosų padaugės, tai yra teigiamų atsiliepimų pavyzdys; lydekos, mintančios karosais, mažina jų skaičių – tai neigiamų atsiliepimų pavyzdys; didėjant plėšrūnų skaičiui, mažėja aukų skaičius, o plėšrūnas, kuriam trūksta maisto, taip pat mažina savo populiacijos augimą; pabaigoje nagrinėjamame tvenkinyje nusistovi dinamiška pusiausvyra tiek lydekų, tiek karosų gausoje. Nuolat palaikoma pusiausvyra, kuri neleistų išnykti bet kurios trofinės grandinės grandies (64 pav.).[ ...]
Pereikime prie svarbiausio apibendrinimo, būtent, kad neigiamos sąveikos laikui bėgant tampa mažiau pastebimos, jei ekosistema yra pakankamai stabili ir jos erdvinė struktūra leidžia populiacijas tarpusavyje koreguoti. Plėšrūno-grobio tipo modelių sistemose, aprašytose Lotkos-Volterra lygtimi, jei į lygtį neįvedami papildomi terminai, apibūdinantys populiacijos saviribojimo veiksnių poveikį, tai svyravimai vyksta nuolat ir neišnyksta ( žr. Levontin, 1969). Pimentel (1968; taip pat žr. Pimentel ir Stone, 1968) eksperimentiškai parodė, kad tokie papildomi terminai gali atspindėti abipusį prisitaikymą arba genetinį grįžtamąjį ryšį. Kai iš individų, anksčiau dvejus metus kartu egzistavusių kultūroje, kur jų skaičius smarkiai svyravo, buvo kuriamos naujos kultūros, paaiškėjo, kad jie sukūrė ekologinę homeostazę, kurioje kiekviena populiacija buvo „slopinama“ kitas tiek, kad paaiškėjo, kad jų sambūvis yra stabilesnėje pusiausvyroje.
Dviejų rūšių sąveikos modeliai
Volteros hipotezės. Analogijos su chemine kinetika. Volterra sąveikos modeliai. Sąveikos tipų klasifikacija Konkurencija. Plėšrūnas-grobis. Apibendrinti rūšių sąveikos modeliai . Kolmogorovo modelis. MacArthuro dviejų rūšių vabzdžių sąveikos modelis. Parametrinis ir Bazykin sistemos faziniai portretai.
Italų matematikas Vito Volterra pagrįstai laikomas šiuolaikinės matematinės populiacijų teorijos pradininku, sukūrusiu matematinę biologinių bendrijų teoriją, kurios aparatas yra diferencialinės ir integralinės-diferencialinės lygtys.(Vito Volterra. Lecons sur la Theorie Mathematique de la Lutte pour la Vie. Paris, 1931). Vėlesniais dešimtmečiais populiacijos dinamika vystėsi daugiausia pagal šioje knygoje išsakytas idėjas. Volterros knygos vertimas į rusų kalbą buvo išleistas 1976 m. pavadinimu „Matematinė kovos už būvį teorija“ su Yu.M. Svireževas, kuriame aptariama matematinės ekologijos raidos istorija 1931–1976 m.
Volterros knyga parašyta taip, kaip rašomos knygos apie matematiką. Pirmiausia suformuluojamos tam tikros prielaidos apie matematinius objektus, kurie turėtų būti tiriami, o tada atliekamas matematinis šių objektų savybių tyrimas.
Volterros tyrinėtos sistemos susideda iš dviejų ar daugiau rūšių. Kai kuriais atvejais atsižvelgiama į sunaudoto maisto atsargas. Lygtys, apibūdinančios šių rūšių sąveiką, yra pagrįstos šiais vaizdiniais.
Volteros hipotezės
1. Maisto galima įsigyti neribotais kiekiais, arba jo tiekimas laikui bėgant yra griežtai reguliuojamas.
2. Kiekvienos rūšies individai miršta taip, kad per laiko vienetą žūva pastovi esamų individų dalis.
3. Plėšriosios rūšys valgo grobį, o per laiko vienetą suvalgyto grobio skaičius visada yra proporcingas tikimybei sutikti šių dviejų rūšių individus, t.y. plėšrūnų skaičiaus ir grobio skaičiaus sandauga.
4. Jei maisto yra ribotas kiekis ir kelios rūšys, galinčios jį suvartoti, tai rūšies maisto dalis, suvartota per laiko vienetą, yra proporcinga šios rūšies individų skaičiui, imant tam tikrą koeficientą, priklausantį apie rūšis (tarprūšinės konkurencijos modeliai).
5. Jei rūšis minta maistu, kurio galima gauti neribotais kiekiais, rūšių skaičiaus padidėjimas per laiko vienetą yra proporcingas rūšies skaičiui.
6. Jei rūšis minta maistu, kurio yra ribotai, tai jos dauginimąsi reguliuoja maisto suvartojimo norma, t.y. per laiko vienetą padidėjimas proporcingas suvalgyto maisto kiekiui.
Analogijos su chemine kinetika
Šios hipotezės turi artimų paralelių su chemine kinetika. Populiacijos dinamikos lygtyse, kaip ir cheminės kinetikos lygtyse, naudojamas „susidūrimų principas“, kai reakcijos greitis proporcingas reaguojančių komponentų koncentracijų sandaugai.
Iš tiesų, pagal Volteros hipotezes, greitis procesas kiekvienos rūšies išnykimas proporcingas rūšies gausumui. Cheminėje kinetikoje tai atitinka kai kurios medžiagos monomolekulinę skilimo reakciją, o matematiniame modelyje – neigiamus tiesinius narius dešinėje lygčių pusėje.
Remiantis cheminės kinetikos sampratomis, dviejų medžiagų sąveikos bimolekulinės reakcijos greitis yra proporcingas šių medžiagų susidūrimo tikimybei, t.y. jų koncentracijos sandauga. Lygiai taip pat, vadovaujantis Volteros hipotezėmis, plėšrūnų dauginimosi greitis (grobio mirtis) yra proporcingas plėšrūno ir grobio susidūrimo tikimybei, t.y. jų skaičių sandauga. Abiem atvejais dvilinijiniai terminai rodomi modelio sistemoje dešinėje atitinkamų lygčių pusėse.
Galiausiai tiesiniai teigiami dėmenys dešinėje Volteros lygčių pusėje, atitinkantys gyventojų skaičiaus augimą neribotomis sąlygomis, atitinka autokatalizinius cheminių reakcijų terminus. Toks lygčių panašumas cheminiuose ir ekologiniuose modeliuose leidžia matematiniam populiacijos kinetikos modeliavimui taikyti tuos pačius tyrimo metodus kaip ir cheminių reakcijų sistemoms.
Sąveikos tipų klasifikacija
Remiantis Volteros hipotezėmis, sąveikauja dvi rūšys, kurių skaičius x 1 ir x 2 galima apibūdinti lygtimis:
(9.1)
Čia parametrai a i - rūšių augimo greičio konstantos, c aš- populiacijos savaime ribojančios konstantos (intraspecifinė konkurencija), b ij– rūšių sąveikos konstantos, (i, j= 1,2). Šių koeficientų ženklai lemia sąveikos tipą.
Biologinėje literatūroje sąveikos paprastai klasifikuojamos pagal susijusius mechanizmus. Įvairovė čia didžiulė: įvairios trofinės sąveikos, cheminės sąveikos tarp bakterijų ir planktoninių dumblių, grybų sąveika su kitais organizmais, augalų organizmų eilės, ypač susijusios su konkurencija dėl saulės šviesos ir su dirvožemio evoliucija ir kt. Tokia klasifikacija atrodo nenusakoma.
E . Odumas, atsižvelgdamas į V. Volterros pasiūlytus modelius, pasiūlė klasifikaciją ne pagal mechanizmus, o pagal rezultatus. Pagal šią klasifikaciją ryšiai turėtų būti vertinami kaip teigiami, neigiami arba neutralūs, atsižvelgiant į tai, ar vienos rūšies gausa didėja, mažėja ar išlieka nepakitusi esant kitai rūšiai. Tada pagrindinius sąveikos tipus galima pateikti lentelės pavidalu.
RŪŠIŲ SĄVEIKOS TIPAI
|
SIMBIOZĖ |
b 12 ,b 21 >0 |
||
|
KOMENSALIZMAS |
b 12 ,>0, b 21 =0 |
||
|
PREDATOR-Grobis |
b 12 ,>0, b 21 <0 |
||
|
AMENZALIZMAS |
b 12 ,=0, b 21 <0 |
||
|
VARZYBOS |
b 12 , b 21 <0 |
||
|
NEUTRALIZMAS |
b 12 , b 21 =0 |
Paskutiniame stulpelyje rodomi sąveikos koeficientų ženklai iš sistemos (9.1)
Apsvarstykite pagrindinius sąveikos tipus
KONKURSŲ LYGTYBĖS:
Kaip matėme 6 paskaitoje, konkurencijos lygtys yra šios:
 (9.2)
(9.2)
Stacionarių sistemų sprendimai:
(1).
![]()
Bet kokių sistemos parametrų koordinačių pradžia yra nestabilus mazgas.
(2).
![]() (9.3)
(9.3)
C stacionari būsena (9.3) yra balnas ties a 1 >b 12 /Su 2 ir
stabilus mazgas ties a 1 12 /s 2 . Ši sąlyga reiškia, kad rūšis išnyksta, jei jos augimo tempas yra mažesnis už tam tikrą kritinę vertę.
(3).
![]() (9.4)
(9.4)
C stacionarus tirpalas (9.4)¾ balno at a 2 >b 21 /c 1 ir stabilus mazgas ties a 2< b 21 /c 1
(4).
![]() (9.5)
(9.5)
Stacionari būsena (9.5) apibūdina dviejų konkuruojančių rūšių sambūvį ir yra stabilus mazgas, jei įvykdomas ryšys:
![]()
Tai reiškia nelygybę:
b 12
b 21
kuri leidžia suformuluoti rūšių sambūvio sąlygą:
Tarppopuliacijų sąveikos koeficientų sandauga yra mažesnė už populiacijos sąveikos koeficientų sandaugą.
Iš tiesų, tegul natūralūs šių dviejų rūšių augimo tempaia 1 , a 2 yra tas pats. Tada būtina stabilumo sąlyga
c 2 > b 12 ,c 1 >b 21 .
Šios nelygybės rodo, kad vieno iš konkurentų skaičiaus padidėjimas jo paties augimą slopina stipriau nei kito konkurento augimas. Jei abiejų rūšių gausą iš dalies arba visiškai riboja skirtingi ištekliai, aukščiau nurodytos nelygybės galioja. Jei abiejų rūšių poreikiai yra visiškai vienodi, tada viena iš jų bus gyvybingesnė ir išstums savo konkurentą.
Sistemos fazių trajektorijų elgsena vizualiai parodo galimus konkurencijos rezultatus. Dešiniąsias sistemos (9.2) lygčių puses prilyginame nuliui:
x 1 (a 1-c 1 x 1 – b 12 x 2) = 0 (dx 1 /dt = 0),
x 2 (a 2 –b 21 x 1 – c 2 x 2) = 0 (dx 2 /dt = 0),
Šiuo atveju gauname pagrindinių sistemos izoklinijų lygtis
x 2 = – b 21 x 1 / c 2 +a 2/c2, x 2 = 0
yra vertikaliųjų liestinių izoklinijų lygtys.
x 2 = – c 1 x 1 /b12+ a 1 /b 12 , x 1 = 0
yra vertikaliųjų liestinių izoklinijų lygtys. Vertikalių ir horizontalių liestinių sistemų izoklinijų porų susikirtimo taškai yra lygčių sistemos (9.2.) stacionarūs sprendiniai ir jų koordinatės ![]() yra stacionarus konkuruojančių rūšių skaičius.
yra stacionarus konkuruojančių rūšių skaičius.
Galima pagrindinių izoklinų vieta sistemoje (9.2) parodyta 9.1 pav. Ryžiai. 9.1aatitinka rūšies išlikimąx 1, pav. 9.1 b- rūšies išlikimasx 2, pav. 9.1 in– rūšių sambūvis pagal sąlygas (9.6). 9.1 pavGdemonstruoja paleidimo sistemą. Čia konkurso rezultatas priklauso nuo pradinių sąlygų. Stacionari būsena (9.5), kuri abiem tipams nėra lygi nuliui, yra nestabili. Tai yra balnas, per kurį praeina separatorius, atskirdamas kiekvienos rūšies išlikimo sritis.

Ryžiai. 9.1.Pagrindinių izoklinų išsidėstymas Volteros dviejų tipų (9.2) konkurencijos sistemos faziniame portrete su skirtingais parametrų santykiais. Paaiškinimai tekste.
Norint ištirti rūšių konkurenciją, buvo atlikti eksperimentai su įvairiais organizmais. Paprastai atrenkamos dvi glaudžiai susijusios rūšys ir auginamos kartu bei atskirai griežtai kontroliuojamomis sąlygomis. Tam tikrais laiko tarpais atliekamas visiškas arba atrankinis gyventojų surašymas. Įrašykite kelių kartotinių eksperimentų duomenis ir analizuokite. Tyrimai buvo atlikti su pirmuoniais (ypač blakstienomis), daugeliu Tribolium, Drosophila genties vabalų rūšių ir gėlavandenių vėžiagyvių (dafnijų). Buvo atlikta daug eksperimentų su mikrobų populiacijomis (žr. 11 paskaitą). Eksperimentai taip pat buvo atliekami gamtoje, įskaitant planarijas (Reynolds), dvi skruzdėlių rūšis (Pontin) ir kt. 9.2. parodytos diatomų, naudojančių tą patį išteklius (užimančių tą pačią ekologinę nišą), augimo kreivės. Kai auginama monokultūroje Asterionella formosa pasiekia pastovų tankio lygį ir palaiko nuolat žemą resurso (silikato) koncentraciją. B. Kai auginama monokultūroje Synedrauina elgiasi panašiai ir palaiko dar žemesnę silikato koncentraciją. B. Auginant kartu (dviem egzemplioriais) Synedrauina nukonkuruoja Asterionella formosa. Matyt, Synedra

Ryžiai. 9.2.Konkurencija diatomuose. a - kai auginami monokultūroje Asterionella formosa pasiekia pastovų tankio lygį ir palaiko nuolat žemą resurso (silikato) koncentraciją. b - kai auginami monokultūroje Synedrauina elgiasi panašiai ir palaiko dar žemesnę silikato koncentraciją. į - auginant kartu (dviem egzemplioriais) Synedruina nukonkuruoja Asterionella formosa. Matyt, Synedra laimi konkursą dėl gebėjimo visapusiškiau išnaudoti substratą (taip pat žr. 11 paskaitą).
Plačiai žinomi G. Gauso konkurencijos tyrimo eksperimentai, parodantys vienos iš konkuruojančių rūšių išlikimą ir leidžiantys suformuluoti „konkurencinės atskirties dėsnį“. Įstatymas teigia, kad vienoje ekologinėje nišoje gali egzistuoti tik viena rūšis. Ant pav. 9.3. pateikiami Gause eksperimentų rezultatai dviem parametium rūšims, užimančioms tą pačią ekologinę nišą (9.3 pav. a, b) ir rūšims, užimančioms skirtingas ekologines nišas (9.3 pav. c).

Ryžiai. 9.3. a- Dviejų rūšių populiacijos augimo kreivės Parametiumas vienos rūšies kultūrose. Juodi apskritimai - P Aurelija, balti apskritimai - P. Caudatum
b- P aurelijos ir P augimo kreivės. Caudatum mišrioje kultūroje.
Gausas, 1934 m
Konkurencijos modelis (9.2) turi trūkumų, visų pirma, iš to seka, kad dviejų rūšių sambūvis galimas tik tuo atveju, jei jų gausą riboja skirtingi veiksniai, tačiau modelis nenurodo, kokie dideli skirtumai turi būti, kad būtų užtikrintas ilgalaikis sambūvis. . Kartu žinoma, kad ilgalaikiam sambūviui besikeičiančioje aplinkoje reikalingas skirtumas, siekiantis tam tikrą vertę. Stochastinių elementų įvedimas į modelį (pavyzdžiui, išteklių naudojimo funkcijos įvedimas) leidžia kiekybiškai ištirti šiuos klausimus.
Predator + grobis sistema
 (9.7)
(9.7)
Čia, priešingai nei (9.2), ženklai b 12 ir b 21 - kitoks. Kaip ir konkurencijos atveju, kilmė
![]() (9.8)
(9.8)
yra vienaskaita nestabilaus mazgo tipo taškas. Trys kitos galimos stacionarios būsenos:
![]() ,(9.9)
,(9.9)
![]() (9.10)
(9.10)
![]() (9.11)
(9.11)
Taigi galimas tik grobis (9.10), tik plėšrūnas (9.9) (jei turi kitų maisto šaltinių) ir abiejų rūšių sambūvis (9.11). Paskutinį variantą mes jau svarstėme 5 paskaitoje. Galimi plėšrūno-grobio sistemos fazinių portretų tipai parodyti pav. 9.4.
Horizontaliųjų liestinių izoklinijos yra tiesios
x 2 = – b 21 X 1 /c 2 + a 1/c2, X 2 = 0,
o vertikaliųjų liestinių izoklinas– tiesus
x 2 = - c 1 X 1 /b 12 + a 2 /b 12 , X 1 = 0.
Stacionarūs taškai yra vertikalių ir horizontalių liestinių izoklinijų sankirtoje.

Iš pav. 9.4 matosi taip. plėšrūno-grobio sistema (9.7) gali turėti stabilią pusiausvyros padėtį, kurioje o romo aukų populiacija yra visiškai išnykusi ( ) ir liko tik plėšrūnai (taškas 2 pav. 9.4 a). Akivaizdu, kad tokia situacija gali būti realizuota tik tuo atveju, jei, be nagrinėjamų aukų tipo, X 1 plėšrūnas X 2 - turi papildomų maitinimo šaltinių. Šį faktą modelyje atspindi teigiamas žodis, esantis x 2 lygties dešinėje. Vienetiniai taškai(1) ir (3) (9.4 pav.). a) yra nestabilūs. Antra galimybė – stabili stacionari būklė, kai plėšrūnų populiacija visiškai išmirė ir liko tik aukos – stabilus taškas(3) (9.4 pav 6 ). Čia yra ypatingas taškas (1) – taip pat nestabilus mazgas.
Galiausiai trečia galimybė – stabilus plėšrūnų ir grobio populiacijų sambūvis (1 pav.). 9.4 in), kurių stacionarios gausos išreiškiamos formulėmis (9.11).
Kaip ir vienos populiacijos atveju (žr. 3 paskaitą), modeliui (9.7) galima sukurti stochastinį modelį, bet jo negalima aiškiai išspręsti. Todėl apsiribojame bendrais samprotavimais. Tarkime, kad, pavyzdžiui, pusiausvyros taškas yra tam tikru atstumu nuo kiekvienos ašies. Tada fazių trajektorijoms, kuriose reikšmėsx 1 , x 2 išliks pakankamai didelis, deterministinis modelis bus gana patenkinamas. Bet jei tam tikru fazės trajektorijos tašku koks nors kintamasis nėra labai didelis, atsitiktiniai svyravimai gali tapti reikšmingi. Jie lemia tai, kad reprezentacinis taškas persikels į vieną iš ašių, o tai reiškia atitinkamos rūšies išnykimą.
Taigi stochastinis modelis pasirodo nestabilus, nes stochastinis „dreifas“ anksčiau ar vėliau veda prie vienos rūšies išnykimo. Taikant tokį modelį, plėšrūnas galiausiai miršta atsitiktinai arba dėl to, kad pirmiausia pašalinama jo grobio populiacija. Stochastinis plėšrūno ir grobio sistemos modelis gerai paaiškina Gause eksperimentus (Gause, 1934), kuriame blakstienas Paramettum candatum tarnavo kaip grobis kitam blakstienai Didinium nasatum – plėšrūnas. Tikimasi pagal deterministines lygtis (9.7) pusiausvyros skaičiai šiuose eksperimentuose buvo maždaug tik penki kiekvienos rūšies individai, todėl nieko stebėtino, kad kiekviename kartotiniame eksperimente arba plėšrūnai, arba grobis (o vėliau ir plėšrūnai) gana greitai išmirė. Pateikiami eksperimentų rezultatai. pav. 9.5.

Ryžiai. 9.5. Augimas Parametium caudatum ir plėšriųjų blakstienų Dadinium nasutum. Nuo : Gause G.F. Kova už būvį. Baltimorė, 1934
Taigi, Volterra rūšių sąveikos modelių analizė rodo, kad nepaisant didelės tokių sistemų elgsenos tipų įvairovės, konkuruojančių rūšių modelyje išvis negali būti neslopinamų populiacijos svyravimų. Tačiau tokie svyravimai pastebimi gamtoje ir eksperimentuose. Jų teorinio paaiškinimo poreikis buvo viena iš priežasčių, kodėl modelių aprašymai buvo suformuluoti bendresne forma.
Apibendrinti dviejų tipų sąveikos modeliai
Buvo pasiūlyta daug modelių, apibūdinančių rūšių sąveiką, kurių lygčių dešinės pusės buvo sąveikaujančių populiacijų dydžių funkcijos. Buvo aptartas bendrųjų kriterijų, leidžiančių nustatyti, kokio tipo funkcijos gali apibūdinti laikino populiacijos dydžio elgseną, įskaitant stabilius svyravimus, kūrimo klausimas. Žinomiausi iš šių modelių yra Kolmogorovo (1935 m., peržiūrėta 1972 m.) ir Rosenzweigo (1963 m.).
 (9.12)
(9.12)
Modelis pagrįstas šiomis prielaidomis:
1) Plėšrūnai tarpusavyje nebendrauja, t.y. plėšrūnų veisimosi greitis k 2 ir aukų skaičius L, kurį per laiko vienetą išnaikina vienas plėšrūnas, nepriklauso nuo y.
2) Grobio skaičiaus padidėjimas esant plėšrūnams yra lygus padidėjimui, kai nėra plėšrūnų, atėmus plėšrūnų išnaikinto grobio skaičių. Funkcijos k 1 (x), k 2 (x), L(x), yra ištisinės ir apibrėžtos teigiamoje pusašėje x, y³ 0.
3) dk 1 /dx< 0. Tai reiškia, kad grobio dauginimo koeficientas nesant plėšrūno monotoniškai mažėja didėjant grobio skaičiui, o tai atspindi ribotus maisto ir kitus išteklius.
4) dk 2 /dx> 0, k 2 (0) < 0 < k 2 (¥ ). Didėjant grobio skaičiui, plėšrūnų dauginimo koeficientas monotoniškai mažėja didėjant grobio skaičiui, pereinant nuo neigiamų verčių (kai nėra ko valgyti) prie teigiamų.
5) Vieno plėšrūno per laiko vienetą išnaikintų aukų skaičius L(x)> 0 adresu N> 0; L(0)=0.
Sistemos (9.12) fazinių portretų galimi tipai parodyti pav. 9.6:

Ryžiai. 9.6.Kolmogorovo sistemos faziniai portretai (9.12), apibūdinantys dviejų tipų sąveiką esant skirtingiems parametrų santykiams. Paaiškinimai tekste.
Stacionarūs sprendimai (jų yra du ar trys) turi šias koordinates:
(1). ` x=0;` y=0.
Bet kurių parametrų reikšmių koordinačių pradžia yra balnas (9.6 pav. a-d).
(2). ` x=A,` y=0.(9.13)
Anustatoma iš lygties:
k 1 (A)=0.
Stacionarus sprendimas (9.13) yra balnas, jei B< A (9.6 pav a, b, G), B nustatoma iš lygties
k 2 (B)=0
Taškas (9.13) dedamas į teigiamą kvadrantą, jei B>A . Tai stabilus mazgas .
Paskutinis atvejis, atitinkantis plėšrūno mirtį ir grobio išgyvenimą, parodytas Fig. 9.6 in.
(3). ` x=B,` y=C.(9.14)
C reikšmė nustatoma pagal lygtis:
Taškas (9.14) – židinys (9.6 pav.). a) arba mazgas (9.6 pav G), kurio stabilumas priklauso nuo kiekio ženklos
s 2 = – k 1 (B)-k 1 (B)B+L(B)C.
Jeigu s>0, taškas yra stabilus, jeis<0 ‑ точка неустойчива, и вокруг нее могут существовать предельные циклы (рис. 9.6 b)
Užsienio literatūroje dažniau svarstomas panašus Rosenzweig ir MacArthur (1963) pasiūlytas modelis:
 (9.15)
(9.15)
kur f(x) – aukų skaičiaus kitimo tempas x nesant plėšrūnų, F( x,y) yra grobuonystės intensyvumas, k- koeficientas, apibūdinantis grobio biomasės pavertimo plėšrūnų biomase efektyvumą, e- Plėšrūnų mirtingumas.
Modelis (9.15) redukuojasi iki konkretaus Kolmogorovo modelio (9.12) atvejo pagal šias prielaidas:
1) plėšrūnų skaičių riboja tik grobio skaičius,
2) greitis, kuriuo konkretus plėšrūno individas suėda grobį, priklauso tik nuo grobio populiacijos tankio ir nepriklauso nuo plėšrūnų populiacijos tankio.
Tada lygtys (9.15) įgauna formą.
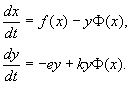
Apibūdinant realių rūšių sąveiką, teisingos lygčių dalys konkretizuojamos pagal idėjas apie biologines realijas. Apsvarstykite vieną iš populiariausių šio tipo modelių.
Dviejų rūšių vabzdžių sąveikos modelis (MacArthur, 1971)
Modelis, kurį aptarsime toliau, buvo naudojamas sprendžiant praktinę kenkėjų kontrolės problemą sterilizuojant vienos rūšies patinus. Remiantis biologinėmis rūšių sąveikos ypatybėmis, buvo parašytas toks modelis
 (9.16)
(9.16)
Čia x,y- dviejų rūšių vabzdžių biomasė. Šiame modelyje aprašytų rūšių trofinė sąveika yra labai sudėtinga. Tai lemia dešiniosiose lygčių pusėse esančių polinomų formą.
Apsvarstykite pirmosios lygties dešinę pusę. Vabzdžių rūšys X valgo rūšies lervas adresu(narys + k 3 y), bet rūšies suaugusieji adresu valgo rūšies lervas X priklauso daugybei rūšių X arba adresu arba abiejų rūšių (nariai – k 4 xy, – y 2). Prie mažų X rūšių mirtingumas X didesnis nei natūralus prieaugis (1 –k 1 +k 2 x–x 2 < 0 prie mažų X). Antroje lygtyje terminas k 5 atspindi natūralų rūšies augimą y; –k 6 y- tokio pobūdžio susivaldymas,–k 7 x- mintančios rūšies lervos adresu rūšies vabzdžiai x, k 8 xy – rūšių biomasės augimas adresu suėsdami suaugę šios rūšies vabzdžiai adresu rūšies lervos X.
Ant pav. 9.7 pateikiamas ribinis ciklas, kuris yra stabilaus periodinio sistemos sprendimo trajektorija (9.16).

Išspręsti klausimą, kaip užtikrinti populiacijos sugyvenimą su jos biologine aplinka, žinoma, negalima gauti neatsižvelgus į konkrečios biologinės sistemos specifiką ir visų jos tarpusavio ryšių analizę. Kartu formalių matematinių modelių tyrimas leidžia atsakyti į kai kuriuos bendruosius klausimus. Galima teigti, kad (9.12) tipo modeliams populiacijų suderinamumo ar nesuderinamumo faktas nepriklauso nuo jų pradinio dydžio, o yra nulemtas tik rūšių sąveikos pobūdžio. Modelis padeda atsakyti į klausimą: kaip paveikti biocenozę, ją valdyti, kad kenksmingos rūšys būtų kuo greičiau sunaikintos.
Valdymas gali būti sumažintas iki trumpalaikio, spazminio populiacijos dydžio pasikeitimo X ir y.Šis metodas atitinka tokius kontrolės metodus kaip vienos ar abiejų populiacijų sunaikinimas cheminėmis priemonėmis. Iš aukščiau suformuluoto teiginio matyti, kad suderinamoms populiacijoms šis valdymo būdas bus neveiksmingas, nes laikui bėgant sistema vėl pasieks stacionarų režimą.
Kitas būdas yra pakeisti sąveikos funkcijų tipą tarp tipų, pavyzdžiui, keičiant sistemos parametrų reikšmes. Būtent šį parametrinį metodą atitinka biologiniai kovos metodai. Taigi, įvedus sterilizuotus patinus, natūralaus populiacijos prieaugio koeficientas mažėja. Jei tuo pačiu metu gausime kito tipo fazinį portretą, kuriame yra tik stabili stacionari būsena su nuliu kenkėjų skaičiumi, kontrolė leis pasiekti norimą rezultatą. – kenkėjų populiacijos sunaikinimas. Įdomu pastebėti, kad kartais patartina poveikį taikyti ne pačiam kenkėjui, o jo partneriui. Kuris iš metodų efektyvesnis, apskritai pasakyti neįmanoma. Tai priklauso nuo turimų valdymo priemonių ir nuo aiškios funkcijų, apibūdinančių populiacijų sąveiką, formos.
Modelis A.D.Bazykinas
Išsamiausiai rūšių sąveikos modelių teorinė analizė atlikta A. D. Bazykino knygoje „Sąveikaujančių populiacijų biofizika“ (M., Nauka, 1985).
Apsvarstykite vieną iš šioje knygoje tyrinėtų plėšrūnų ir grobio modelių.
 (9.17)
(9.17)
Sistema (9.17) – tai paprasčiausio Volteros plėšrūno-grobio modelio (5.17) apibendrinimas, atsižvelgiant į plėšrūnų prisotinimo efektą. Modelyje (5.17) daroma prielaida, kad grobio ganymosi intensyvumas didėja tiesiškai didėjant grobio tankiui, o tai neatitinka tikrovės esant dideliam grobio tankiui. Plėšrūnų mitybos priklausomybei nuo grobio tankio apibūdinti galima pasirinkti įvairias funkcijas. Svarbiausia, kad pasirinkta funkcija didėja x asimptotiškai linksta į pastovią vertę. Modelis (9.6) naudojo logistinę priklausomybę. Bazykin modelyje kaip tokia funkcija pasirenkama hiperbolė x/(1+px). Prisiminkite, kad Monod formulė, kuri apibūdina mikroorganizmų augimo greičio priklausomybę nuo substrato koncentracijos, turi tokią formą. Čia grobis veikia kaip substratas, o plėšrūnas – kaip mikroorganizmai. .
Sistema (9.17) priklauso nuo septynių parametrų. Parametrų skaičių galima sumažinti keičiant kintamuosius:
x® (REKLAMA)x; y ® (REKLAMA)/y;
t® (1/A)t; g (9,18)
ir priklauso nuo keturių parametrų.
Norint atlikti pilną kokybinį tyrimą, būtina keturių dimensijų parametrų erdvę suskirstyti į regionus su skirtingo tipo dinamine elgsena, t.y. sukurti parametrinį arba struktūrinį sistemos portretą.
Tada reikia sukurti fazinius portretus kiekvienam parametrinio portreto regionui ir aprašyti bifurkacijas, atsirandančias su faziniais portretais skirtingų parametrinio portreto sričių ribose.
Viso parametrinio portreto konstravimas atliekamas kaip mažo matmens parametrinio portreto „pjūvių“ (projekcijų) rinkinys su fiksuotomis kai kurių parametrų reikšmėmis.
Parametrinis sistemos portretas (9.18) fiksuotam g ir mažas e parodyta 9.8 pav. Portrete yra 10 sričių su skirtingais fazės trajektorijos elgesio tipais.

Ryžiai. 9.8.Parametrinis sistemos portretas (9.18) fiksuotamg
ir mažas e
Sistemos elgsena su skirtingais parametrų santykiais gali labai skirtis (9.9 pav.). Sistemoje galimi šie dalykai:
1) viena stabili pusiausvyra (1 ir 5 regionai);
2) vienas stabilus ribinis ciklas (3 ir 8 regionai);
3) dvi stabilios pusiausvyros (2 regionas)
4) stabilus ribinis ciklas ir nestabili pusiausvyra jame (6, 7, 9, 10 regionai)
5) stabilus ribinis ciklas ir stabili pusiausvyra už jo ribų (4 sritis).
7, 9, 10 parametrinėse srityse pusiausvyros traukos sritį riboja nestabilus ribinis ciklas, esantis stabilios zonos viduje. Įdomiausias yra fazinis portretas, atitinkantis 6 sritį parametriniame portrete. Tai išsamiai parodyta fig. 9.10.

Pusiausvyros B 2 traukos sritis (tamsuota) yra „sraigė“, besisukanti iš nestabilaus židinio B 1 . Jei žinoma, kad pradiniu laiko momentu sistema buvo šalia B 1, tada galima spręsti, ar atitinkama trajektorija pasieks pusiausvyrą B 2, ar į stabilų ribinį ciklą, supantį tris pusiausvyros taškus C ( balnas), B 1 ir B 2 tik remiantis tikimybiniais sumetimais.

9.10 pav.9.18 sistemos fazinis portretas, skirtas 6 parametrinei sričiai. Pritraukimo sritis B 2 užtamsinta
Ant parametrinio portreto(9.7) yra 22 susidarančios įvairios bifurkacijos ribos 7 įvairių tipų bifurkacijos. Jų tyrimas leidžia nustatyti galimus sistemos elgesio tipus, kai keičiasi jos parametrai. Pavyzdžiui, kai juda iš teritorijos 1 į 3 sritį gimsta mažas ribinis ciklas arba švelniai gimsta savaiminiai svyravimai aplink vieną pusiausvyrą AT. Panašus minkštas savaiminių virpesių gimimas, bet aplink vieną iš pusiausvyros, būtent B 1 , atsiranda kertant regionų sieną 2 ir 4. Judant iš teritorijos 4 iki 5 srities stabilus ribinis ciklas aplink taškąB 1 „sprogsta“ separatrikso kilpoje ir vienintelis traukiantis taškas yra pusiausvyra B 2 ir tt
Be abejo, ypač įdomu praktikai sistemos artumo prie bifurkacijos ribos kriterijų kūrimas. Iš tiesų, biologai puikiai žino natūralių ekologinių sistemų „buferinę“ arba „lankstumo“ savybę. Šie terminai paprastai reiškia sistemos gebėjimą sugerti išorinį poveikį. Kol išorinio veiksmo intensyvumas neviršija tam tikros kritinės vertės, sistemos elgsena nevyksta kokybinių pokyčių. Fazinėje plokštumoje tai atitinka sistemos grįžimą į stabilią pusiausvyros būseną arba į stabilų ribinį ciklą, kurio parametrai nedaug skiriasi nuo pradinio. Kai smūgio intensyvumas viršija leistiną, sistema „suyra“, pereina į kokybiškai skirtingą dinaminio elgesio režimą, pavyzdžiui, tiesiog užgęsta. Šis reiškinys atitinka bifurkacijos perėjimą.
Kiekvienas bifurkacinių perėjimų tipas turi savo išskirtinių bruožų, leidžiančių spręsti apie tokio perėjimo pavojų ekosistemai. Štai keletas bendrų kriterijų, liudijančių apie pavojingos ribos artumą. Kaip ir vienos rūšies atveju, jei sumažėjus vienos rūšies skaičiui sistema „užstringa“ šalia nestabilaus balno taško, o tai išreiškiama labai lėtu skaičiaus atkūrimu iki pradinės vertės, tada sistema yra netoli kritinės ribos. Plėšrūnų ir grobio skaičiaus svyravimų formos pokyčiai taip pat yra pavojaus rodiklis. Jei svyravimai tampa relaksaciniais iš artimų harmoninių, o svyravimų amplitudė didėja, tai gali lemti sistemos stabilumo praradimą ir vienos rūšies išnykimą.
Toliau gilinant matematinę rūšių sąveikos teoriją, detalizuojama pačių populiacijų struktūra ir atsižvelgiama į laiko ir erdvės veiksnius.
Literatūra.
Kolmogorovas A.N. Kokybinis populiacijos dinamikos matematinių modelių tyrimas. // Kibernetikos problemos. M., 1972, 5 leidimas.
MacArtur R. Grafinė ekologinių sistemų analizė// Biologijos ataskaitos skyrius Perinceton University. 1971
AD Bazykin „Sąveikaujančių populiacijų biofizika“. M., Nauka, 1985 m.
W. Volterra: „Matematinė kovos už būvį teorija“. M.. Mokslas, 1976 m
Marlė G.F. Kova už būvį. Baltimorė, 1934 m.