مفهوم مهم في الرياضيات هو وظيفة. بمساعدتها ، يمكنك تصور العديد من العمليات التي تحدث في الطبيعة ، وتعكس العلاقة بين كميات معينة باستخدام الصيغ والجداول والصور على الرسم البياني. مثال على ذلك هو اعتماد ضغط الطبقة السائلة على الجسم على عمق الانغماس ، والتسارع - على تأثير قوة معينة على الجسم ، وزيادة درجة الحرارة - على الطاقة المنقولة ، والعديد من العمليات الأخرى. تتضمن دراسة الوظيفة رسم رسم بياني ، ومعرفة خصائصه ، ومجال التعريف والقيم ، وفترات الزيادة والنقصان. نقطة مهمةفي هذه العملية يتم إيجاد النقاط القصوى. حول كيفية القيام بذلك بشكل صحيح ، وسوف تستمر المحادثة.
حول المفهوم نفسه في مثال محدد
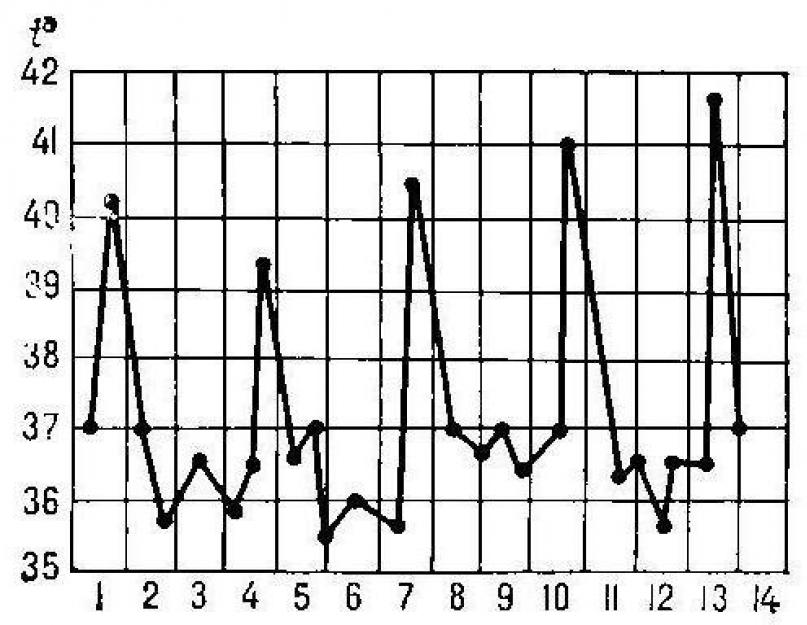
في الطب ، يمكن لبناء الرسم البياني للوظيفة أن يخبرنا عن مسار تطور المرض في جسم المريض ، مما يعكس حالته بوضوح. لنفترض أن الوقت بالأيام مرسوم على طول محور OX ، وأن درجة حرارة جسم الإنسان مخططة على طول محور OY. يوضح الشكل بوضوح كيف يرتفع هذا المؤشر بشكل حاد ثم ينخفض. من السهل أيضًا ملاحظة النقاط الفردية التي تعكس اللحظات التي تبدأ فيها الوظيفة ، بعد أن زادت سابقًا ، في الانخفاض ، والعكس صحيح. هذه هي النقاط القصوى ، أي القيم الحرجة (الحد الأقصى والحد الأدنى) في هذه القضيةدرجة حرارة المريض ، وبعد ذلك تحدث تغيرات في حالته.

زاوية الميل
من السهل تحديد كيف يتغير مشتق الوظيفة من الشكل. إذا ارتفعت الخطوط المستقيمة في الرسم البياني بمرور الوقت ، فهذا يعني أنها موجبة. وكلما كانت أكثر انحدارًا ، فإن قيمة أكبريأخذ المشتق مع زيادة الميل. خلال فترات الانخفاض ، تأخذ هذه القيمة القيم السالبة، بالتحول إلى الصفر عند النقاط القصوى ، ويتم رسم الرسم البياني للمشتق في الحالة الأخيرة بالتوازي مع محور OX.
يجب التعامل مع أي عملية أخرى بنفس الطريقة. لكن أفضل شيء في هذا المفهوم يمكن أن يخبرنا بالحركة مختلف الهيئاتيظهر بوضوح في الرسوم البيانية.
حركة المرور
افترض أن شيئًا ما يتحرك في خط مستقيم ، ويكتسب السرعة بشكل موحد. خلال هذه الفترة ، يمثل التغيير في إحداثيات الجسم بيانياً منحنى معينًا ، والذي قد يسميه عالم الرياضيات فرعًا من القطع المكافئ. في الوقت نفسه ، تتزايد الوظيفة باستمرار ، حيث تتغير مؤشرات الإحداثيات بشكل أسرع وأسرع مع كل ثانية. يوضح الرسم البياني للسرعة سلوك المشتق الذي تزداد قيمته أيضًا. هذا يعني أن الحركة ليس لديها نقاط حرجة.
سيستمر هذا إلى أجل غير مسمى. ولكن ماذا لو قرر الجسم فجأة أن يبطئ ، ويتوقف ويبدأ في التحرك في اتجاه مختلف؟ في هذه الحالة ، ستبدأ مؤشرات التنسيق في الانخفاض. وستمرر الدالة قيمة حرجة وتتحول من الزيادة إلى التناقص.

في هذا المثال ، يمكنك أن تفهم مرة أخرى أن النقاط القصوى على الرسم البياني للوظيفة تظهر في اللحظات التي تتوقف فيها عن أن تكون رتيبة.
المعنى المادي للمشتق
ما تم وصفه سابقًا أظهر بوضوح أن المشتق هو في الأساس معدل تغير الوظيفة. يحتوي هذا الصقل على معناه المادي. النقاط القصوى هي مناطق حرجة على الرسم البياني. من الممكن اكتشافها واكتشافها من خلال حساب قيمة المشتق ، والتي تبين أنها تساوي صفرًا.
هناك علامة أخرى ، وهي شرط كافٍ لأقصى حد. المشتق في أماكن الانعطاف هذه يغير علامته: من "+" إلى "-" في منطقة الحد الأقصى ومن "-" إلى "+" في منطقة الحد الأدنى.

الحركة تحت تأثير الجاذبية
لنتخيل حالة أخرى. كان الأطفال يلعبون الكرة ، وألقوها بطريقة بدأت تتحرك بزاوية في الأفق. في اللحظة الأولى ، السرعة هذا الكائنكان الأكبر ، ولكن تحت تأثير الجاذبية بدأ في الانخفاض ، ومع كل ثانية بنفس القيمة ، تساوي تقريبًا 9.8 م / ث 2. هذه هي قيمة التسارع الذي يحدث تحت تأثير جاذبية الأرض أثناء السقوط الحر. على سطح القمر ، سيكون أصغر بنحو ستة أضعاف.
الرسم البياني الذي يصف حركة الجسم عبارة عن قطع مكافئ بفروع تتجه نحو الأسفل. كيف تجد النقاط القصوى؟ في هذه الحالة ، هذا هو رأس الدالة ، حيث تكون سرعة الجسم (الكرة) صفرًا. يصبح مشتق الدالة صفرًا. في هذه الحالة ، يتغير الاتجاه ، وبالتالي قيمة السرعة ، إلى الاتجاه المعاكس. الجسم يطير لأسفل مع كل ثانية أسرع وأسرع ، ويتسارع بنفس المقدار - 9.8 م / ث 2.

المشتق الثاني
في الحالة السابقة ، يتم رسم مخطط معامل السرعة كخط مستقيم. يتم توجيه هذا الخط أولاً إلى أسفل ، لأن قيمة هذه الكمية تتناقص باستمرار. بعد أن وصلت إلى الصفر في إحدى النقاط الزمنية ، تبدأ مؤشرات هذه القيمة في الزيادة ، ويتغير اتجاه التمثيل الرسومي لوحدة السرعة بشكل كبير. الآن الخط يشير لأعلى.
السرعة ، كونها مشتق من التنسيق فيما يتعلق بالوقت ، لها أيضًا نقطة حرجة. في هذه المنطقة ، تبدأ الوظيفة ، المتناقصة مبدئيًا ، في الزيادة. هذا هو مكان النقطة القصوى لمشتق الدالة. في هذه الحالة ، يصبح ميل المماس صفرًا. والتسارع ، كونه المشتق الثاني للتنسيق فيما يتعلق بالوقت ، يغير العلامة من "-" إلى "+". وتصبح الحركة من البطء المنتظم متسارعة بشكل منتظم.
الرسم البياني للتسريع
تأمل الآن أربعة أرقام. يعرض كل منهم رسمًا بيانيًا للتغيير بمرور الوقت الكمية الماديةمثل التسارع. في حالة "أ" ، تظل قيمتها موجبة وثابتة. هذا يعني أن سرعة الجسم ، مثل الإحداثيات الخاصة به ، تتزايد باستمرار. إذا تخيلنا أن الكائن سيتحرك بهذه الطريقة لفترة طويلة غير محدودة ، فإن الوظيفة التي تعكس اعتماد الإحداثيات في الوقت سوف تتزايد باستمرار. ويترتب على ذلك أنه لا توجد مناطق حرجة. لا توجد أيضًا نقاط قصوى على الرسم البياني للمشتق ، أي سرعة متغيرة خطيًا.

الأمر نفسه ينطبق على الحالة "ب" مع تسارع موجب ومتزايد باستمرار. صحيح أن الرسوم البيانية للإحداثيات والسرعة ستكون أكثر تعقيدًا إلى حد ما هنا.
عندما يذهب التسارع إلى الصفر
بالنظر إلى الشكل "ب" ، يمكن للمرء أن يلاحظ صورة مختلفة تمامًا تميز حركة الجسم. سيتم تصوير سرعتها بيانياً على أنها قطع مكافئ بفروع تتجه لأسفل. إذا واصلنا الخط الذي يصف التغيير في التسارع حتى يتقاطع مع محور OX ، ثم بعد ذلك ، يمكننا أن نتخيل أنه حتى هذه القيمة الحرجة ، حيث تبين أن التسارع يساوي الصفر ، ستزداد سرعة الجسم أكثر فأكثر. ستكون النقطة القصوى لمشتق دالة الإحداثيات أعلى القطع المكافئ ، وبعد ذلك سيغير الجسم بشكل جذري طبيعة الحركة ويبدأ في التحرك في اتجاه مختلف.
في الحالة الأخيرة ، "G" ، لا يمكن تحديد طبيعة الحركة بدقة. هنا نعلم فقط أنه لا يوجد تسارع لبعض الفترة قيد الدراسة. هذا يعني أن الجسم يمكن أن يظل في مكانه أو أن الحركة تحدث بسرعة ثابتة.
تنسيق مهمة الإضافة
دعنا ننتقل إلى المهام التي غالبًا ما نواجهها عند دراسة الجبر في المدرسة ونعرضها للتحضير للامتحان. يوضح الشكل أدناه الرسم البياني للوظيفة. مطلوب لحساب مجموع النقاط القصوى.

سنفعل ذلك للمحور y من خلال تحديد إحداثيات المناطق الحرجة حيث يتم ملاحظة تغيير في خصائص الوظيفة. ببساطة ، نجد القيم على طول المحور السيني لنقاط الانعطاف ، ثم ننتقل إلى إضافة الحدود الناتجة. وفقًا للرسم البياني ، من الواضح أنهم يأخذون القيم التالية: -8 ؛ -7 ؛ -5 ؛ -3 ؛ -2 ؛ واحد؛ 3. هذا يصل إلى -21 ، وهي الإجابة.
حل مثالي
ليس من الضروري شرح مدى أهمية اختيار الحل الأمثل في أداء المهام العملية. بعد كل شيء ، هناك العديد من الطرق لتحقيق الهدف ، وأفضل طريقة للخروج ، كقاعدة عامة ، هي طريقة واحدة فقط. هذا ضروري للغاية ، على سبيل المثال ، عند تصميم السفن ، سفن الفضاءوالطائرات والهياكل المعمارية للعثور على الشكل الأمثل لهذه الأشياء التي من صنع الإنسان.

تعتمد سرعة المركبات إلى حد كبير على التقليل الكفء للمقاومة التي تتعرض لها عند التحرك عبر الماء والهواء ، وعلى الأحمال الزائدة التي تنشأ تحت تأثير قوى الجاذبية والعديد من المؤشرات الأخرى. تحتاج السفينة في البحر إلى صفات مثل الاستقرار أثناء العاصفة ؛ بالنسبة للسفينة النهرية ، فإن الحد الأدنى من الغاطس مهم. عند حساب التصميم الأمثل ، يمكن أن تعطي النقاط القصوى على الرسم البياني بصريًا فكرة عن أفضل حل لمشكلة معقدة. غالبًا ما يتم حل مهام مثل هذه الخطة في الاقتصاد ، في المجالات الاقتصادية ، في العديد من مواقف الحياة الأخرى.
من التاريخ القديم
حتى الحكماء القدماء شغلت المهام القصوى. نجح العلماء اليونانيون في كشف لغز المناطق والأحجام من خلال الحسابات الرياضية. هم أول من أدركوا أنه على متن طائرة ذات أشكال مختلفة بنفس المحيط ، أكبر مساحةدائما لديه دائرة. وبالمثل ، تُمنح الكرة الحجم الأقصى بين الأجسام الأخرى الموجودة في الفضاء والتي لها نفس مساحة السطح. مكرسة لحل مثل هذه المشاكل شخصيات مشهورةمثل أرخميدس وإقليدس وأرسطو وأبولونيوس. نجح مالك الحزين في العثور على نقاط متطرفة ، والتي ، بعد أن لجأت إلى الحسابات ، قامت ببناء أجهزة بارعة. وشملت هذه الآلات التي تتحرك بواسطة البخار والمضخات والتوربينات التي تعمل على نفس المبدأ.

بناء قرطاج
هناك أسطورة ، تستند حبكةها إلى حل إحدى المهام القصوى. كانت نتيجة نهج الأعمال الذي أظهرته الأميرة الفينيقية ، التي لجأت إلى الحكماء طلباً للمساعدة ، هي بناء قرطاج. قطعة أرضلهذه المدينة القديمة والشهيرة ، قدم ديدو (هذا هو اسم الحاكم) زعيم إحدى القبائل الأفريقية. لم تبد له مساحة التخصيص في البداية كبيرة جدًا ، لأنه وفقًا للعقد كان يجب تغطيتها بجلد أكسيد. لكن الأميرة أمرت جنودها بتقطيعها إلى شرائح رفيعة وإخراج حزام منها. اتضح أنها كانت طويلة جدًا لدرجة أنها غطت منطقة تناسب المدينة بأكملها.
أصول حساب التفاضل والتكامل
والآن دعنا ننتقل من العصور القديمة إلى حقبة لاحقة. من المثير للاهتمام ، أنه في القرن السابع عشر ، طُلب من كبلر فهم أسس التحليل الرياضي من خلال لقاء مع بائع نبيذ. كان التاجر ضليعًا في مهنته لدرجة أنه يمكنه بسهولة تحديد حجم المشروب في البرميل بمجرد إنزال عاصبة حديدية فيه. بالتفكير في مثل هذا الفضول ، تمكن العالم الشهير من حل هذه المعضلة بنفسه. اتضح أن المحاربين الماهرين في تلك الأوقات حصلوا على تعليق صنع الأوعية بطريقة تجعلهم ، عند ارتفاع ونصف قطر معينين لمحيط حلقات التثبيت ، يتمتعون بسعة قصوى.
أصبح هذا بالنسبة لكبلر مناسبة لمزيد من التفكير. توصل بوشر إلى الحل الأمثل من خلال بحث طويل وأخطاء ومحاولات جديدة ، ونقل تجربتهم من جيل إلى جيل. لكن كبلر أراد تسريع العملية وتعلم كيفية القيام بالشيء نفسه في وقت قصير من خلال الحسابات الرياضية. تحولت كل تطوراته ، التي التقطها زملائه ، إلى نظريات معروفة الآن لفيرمات ونيوتن-لايبنيز.
مشكلة إيجاد أقصى مساحة
تخيل أن لدينا سلك طوله 50 سم ، كيف نصنع منه مستطيلاً أكبر مساحة؟
عند البدء في اتخاذ القرار ، يجب على المرء أن ينطلق من حقائق بسيطة ومعروفة. من الواضح أن محيط الشكل سيكون 50 سم ، ويتكون أيضًا من ضعف أطوال كلا الجانبين. هذا يعني أنه ، بعد تحديد أحدهما كـ "X" ، يمكن التعبير عن الآخر كـ (25 - X).
من هنا نحصل على مساحة تساوي X (25 - X). يمكن تمثيل هذا التعبير كدالة تأخذ العديد من القيم. يتطلب حل المشكلة إيجاد الحد الأقصى منها ، مما يعني أنه يجب عليك معرفة النقاط القصوى.
للقيام بذلك ، نجد المشتقة الأولى ونساويها بصفر. النتيجة هي معادلة بسيطة: 25 - 2X = 0.
نتعلم منه أن أحد الأضلاع هو X = 12.5.
لذلك ، آخر: 25 - 12.5 = 12.5.
اتضح أن حل المشكلة سيكون مربعًا طول ضلعه 12.5 سم.

كيف تجد السرعة القصوى
لنفكر في مثال آخر. تخيل أن هناك جسمًا يتم وصف حركته المستقيمة بواسطة المعادلة S = - t 3 + 9t 2 - 24t - 8 ، حيث يتم التعبير عن المسافة المقطوعة بالأمتار ، والوقت بالثواني. مطلوب للعثور على السرعة القصوى. كيف افعلها؟ تم تنزيله ، أوجد السرعة ، أي المشتق الأول.
نحصل على المعادلة: V = - 3t 2 + 18t - 24. الآن ، لحل المشكلة ، نحتاج مرة أخرى إلى إيجاد النقاط القصوى. يجب أن يتم ذلك بنفس الطريقة كما في المهمة السابقة. نوجد المشتق الأول للسرعة ونساويها بصفر.
نحصل على: - 6t + 18 = 0. ومن ثم t = 3 s. هذا هو الوقت الذي تأخذ فيه سرعة الجسم قيمة حرجة. نستبدل البيانات التي تم الحصول عليها في معادلة السرعة ونحصل على: V = 3 m / s.
لكن كيف تعرف ما هو السرعة القصوى، لأن النقاط الحرجة للدالة يمكن أن تكون قيمها الأكبر أو الأصغر؟ للتحقق ، عليك إيجاد المشتق الثاني للسرعة. يتم التعبير عنه بالرقم 6 بعلامة ناقص. هذا يعني أن النقطة التي تم العثور عليها هي الحد الأقصى. وفي حالة وجود قيمة موجبة للمشتق الثاني ، سيكون هناك قيمة صغرى. ومن ثم ، كان الحل الذي تم العثور عليه صحيحًا.
المهام المعطاة كمثال ليست سوى جزء من المهام التي يمكن حلها من خلال القدرة على إيجاد النقاط القصوى للدالة. في الواقع ، هناك الكثير. وتفتح هذه المعرفة إمكانيات غير محدودة للحضارة الإنسانية.
كما ترى ، فإن علامة الحد الأقصى للدالة تتطلب وجود مشتق على الأقل حتى الدرجة الثانية عند النقطة.
مثال.
أوجد القيمة القصوى للدالة.
المحلول.
لنبدأ بالنطاق: 
دعونا نفرق بين الوظيفة الأصلية: 
س = 1، أي أنها نقطة الحد الأقصى المحتمل. نجد المشتق الثاني للدالة ونحسب قيمتها عند س = 1:

لذلك ، من خلال الشرط الثاني الكافي ، س = 1- أقصى نقطة. ثم  هي الحد الأقصى للدالة.
هي الحد الأقصى للدالة.
الرسم التوضيحي.

إجابه:
![]()
الشرط الثالث الكافي لوظيفة ما.
دع الوظيفة ص = و (س)مشتقات تصل إلى ن-الترتيب في الحي من النقطة والمشتقات حتى ن + 1الترتيب في النقطة نفسها. اسمحوا و.
مثال.
أوجد النقاط القصوى للدالة ![]() .
.
المحلول.
الوظيفة الأصلية هي دالة منطقية كاملة ، ومجال تعريفها هو مجموعة الأرقام الحقيقية بأكملها.
لنفرق الوظيفة: 
المشتق يختفي عندما ![]() ، لذلك ، هذه هي نقاط الحد الأقصى المحتمل. دعونا نستخدم الشرط الكافي الثالث لأقصى حد.
، لذلك ، هذه هي نقاط الحد الأقصى المحتمل. دعونا نستخدم الشرط الكافي الثالث لأقصى حد.
نجد المشتق الثاني ونحسب قيمته عند نقاط الحد الأقصى المحتمل (سنحذف الحسابات الوسيطة): 
لذلك ، هي النقطة القصوى (للإشارة الثالثة الكافية من الحد الأقصى ، لدينا ن = 1و ).
لتوضيح طبيعة النقاط ![]() أوجد المشتق الثالث واحسب قيمته في النقاط التالية:
أوجد المشتق الثالث واحسب قيمته في النقاط التالية: 
لذلك ، هي نقطة انعطاف الوظيفة ( ن = 2و ).
يبقى أن نتعامل مع هذه النقطة. نجد المشتق الرابع ونحسب قيمته عند هذه النقطة: 
لذلك ، هي النقطة الدنيا للدالة.
الرسم التوضيحي.

إجابه:
النقطة القصوى هي النقطة الدنيا للدالة.
10. النهايات من وظيفة تعريف الحد الأقصى
يتم استدعاء الوظيفة y = f (x) في ازدياد (يتضاءل) في بعض الفترات إذا كانت لـ x 1< x 2 выполняется неравенство (f(x 1) < f (x 2) (f(x 1) >و (x2)).
إذا زادت دالة قابلة للتفاضل y = f (x) على مقطع ما (تنقص) ، فإن مشتقها في هذا المقطع f "(x) 0
(و "(س) 0).
نقطة x حولاتصل أقصى نقطة محلية (الحد الأدنى) للوظيفة f (x) إذا كان هناك منطقة مجاورة للنقطة x حول، لجميع النقاط التي تكون فيها المتباينة f (x) ≤ f (x o) (f (x) ≥ f (x o)) صحيحة.
يتم استدعاء الحد الأقصى والحد الأدنى من النقاط النقاط القصوى، وقيم الوظيفة في هذه النقاط هي النهايات.
النقاط القصوى
الشروط اللازمة لأقصى حد. إذا كانت النقطة x حولهي نقطة قصوى للدالة f (x) ، فإما أن f "(x o) \ u003d 0 ، أو f (x o) غير موجود. تسمى هذه النقاط حرج،حيث يتم تعريف الوظيفة نفسها عند النقطة الحرجة. يجب البحث عن الحد الأقصى لوظيفة ما بين نقاطها الحرجة.
الشرط الأول الكافي.يترك x حول- نقطة حرجة. إذا كانت f "(x) عند المرور عبر نقطة x حوليغير علامة الجمع إلى ناقص ، ثم عند النقطة x حولالوظيفة لها حد أقصى ، وإلا فسيكون لها حد أدنى. إذا لم يغير المشتق الإشارة عند المرور بنقطة حرجة ، فعندئذٍ عند هذه النقطة x حوللا يوجد حد أقصى.
الشرط الثاني الكافي.دع الدالة f (x) لها مشتق f "(x) في منطقة مجاورة للنقطة x حولوالمشتق الثاني عند النقطة ذاتها x حول. إذا كانت f "(x o) \ u003d 0 ، \ u003e 0 (<0), то точка x حولهي نقطة دنيا (قصوى) محلية للدالة f (x). إذا كانت = 0 ، فيجب على المرء إما استخدام الشرط الكافي الأول أو استخدام مشتقات أعلى.
في مقطع ما ، يمكن أن تصل الوظيفة y = f (x) إلى قيمتها الدنيا أو القصوى إما في النقاط الحرجة أو في نهايات المقطع.
المثال 3.22.أوجد القيمة القصوى للدالة f (x) = 2x 3 - 15x 2 + 36x - 14.
المحلول. بما أن f "(x) \ u003d 6x 2-30x +36 \ u003d 6 (x - 2) (x - 3) ، فإن النقاط الحرجة للوظيفة x 1 \ u003d 2 و x 2 \ u003d 3. يمكن للنقاط القصوى تكون فقط عند هذه النقاط ، فكما هو الحال عند المرور بالنقطة x 1 \ u003d 2 ، يتغير المشتق علامة زائد إلى ناقص ، ثم عند هذه النقطة يكون للوظيفة حد أقصى. التغييرات علامة ناقص إلى زائد ، لذلك ، عند النقطة x 2 \ u003d 3 ، يكون للوظيفة حد أدنى. بعد حساب قيم الوظيفة عند النقطتين x 1 = 2 و x 2 = 3 ، نجد الحد الأقصى لـ الوظيفة: الحد الأقصى f (2) = 14 والحد الأدنى f (3) = 13.
ضع في اعتبارك الرسم البياني للدالة المستمرة ص = و (س)هو مبين في الشكل.
قيمة الوظيفة عند النقطة x 1 سيكون أكبر من قيم الوظيفة في جميع النقاط المجاورة على كل من يسار ويمين xواحد . في هذه الحالة ، يُقال أن الوظيفة موجودة عند النقطة x 1 كحد أقصى. في هذه النقطة xمن الواضح أن الوظيفة 3 لها أيضًا حد أقصى. إذا أخذنا في الاعتبار النقطة x 2 ، فإن قيمة الوظيفة فيه أقل من جميع القيم المجاورة. في هذه الحالة ، يُقال أن الوظيفة موجودة عند النقطة x 2 الحد الأدنى. وبالمثل بالنسبة لهذه النقطة x 4 .
دور ص = و (س)في هذه النقطة x 0 has أقصى، إذا كانت قيمة الوظيفة في هذه النقطة أكبر من قيمها في جميع نقاط بعض الفواصل التي تحتوي على النقطة x 0 ، أي إذا كان هناك حي من هذا القبيل x 0 ، وهو للجميع x≠x 0 , ينتمون إلى هذا الحي ، لدينا عدم المساواة و (خ)<و (x 0 ) .
دور ص = و (س)لديها الحد الأدنىفي هذه النقطة x 0 , إذا كان هناك حي من هذا القبيل x 0 , ما هو للجميع x≠x 0 ينتمون إلى هذا الحي ، لدينا عدم المساواة و (خ)>و (× 0.
النقاط التي تصل فيها الوظيفة إلى الحد الأقصى والحد الأدنى تسمى النقاط القصوى ، وقيم الوظيفة عند هذه النقاط هي الحد الأقصى للدالة.
دعنا ننتبه إلى حقيقة أن الوظيفة المحددة في مقطع ما يمكن أن تصل إلى الحد الأقصى والحد الأدنى فقط في النقاط الواردة في المقطع قيد النظر.
لاحظ أنه إذا كانت الوظيفة لها حد أقصى عند نقطة ما ، فإن هذا لا يعني أنه في هذه المرحلة يكون للوظيفة الحد الأقصى لقيمة في المجال بأكمله. في الشكل الذي تمت مناقشته أعلاه ، الوظيفة عند النقطة x 1 له حد أقصى ، على الرغم من وجود نقاط تكون فيها قيم الوظيفة أكبر منها عند النقطة x 1 . خاصه، F(x 1) < F(x 4) أي الحد الأدنى للدالة أكبر من الحد الأقصى. من تعريف الحد الأقصى ، يتبع فقط أن هذه هي أكبر قيمة للدالة عند نقاط قريبة بدرجة كافية من النقطة القصوى.
النظرية 1. (شرط ضروري لوجود حد أقصى.)إذا كانت وظيفة التفاضل ص = و (س)لديه في هذه النقطة س = س 0 الحد الأقصى ، ثم يتلاشى مشتقه عند هذه النقطة.
دليل - إثبات. دعونا ، من أجل التحديد ، في هذه النقطة x 0 الوظيفة لها حد أقصى. ثم بزيادات صغيرة بما فيه الكفاية Δ xنملك و (x 0 + Δ خ)
تمرير هذه المتباينات إلى النهاية كـ Δ x→ 0 مع مراعاة أن المشتق F "(x 0) موجود ، وبالتالي فإن الحد الموجود على اليسار لا يعتمد على كيفية Δ x→ 0 ، نحصل على: لـ Δ x → 0 – 0 F"(x 0) ≥ 0 وعند Δ x → 0 + 0 F"(x 0) ≤ 0. منذ F"(x 0) عددًا ، فإن هاتين المتراجحتين تتوافقان فقط إذا F"(x 0) = 0.
تنص النظرية التي تم إثباتها على أن الحد الأقصى والحد الأدنى للنقاط يمكن أن يكون فقط من بين قيم الحجة التي يختفي المشتق بسببها.
لقد درسنا الحالة عندما يكون للدالة مشتق في جميع نقاط جزء معين. ماذا يحدث عندما لا يوجد المشتق؟ ضع في اعتبارك الأمثلة.
أمثلة.
- ذ=|x|.
ليس للدالة مشتق عند نقطة ما x= 0 (في هذه المرحلة ، لا يحتوي الرسم البياني للوظيفة على ظل محدد) ، ولكن في هذه المرحلة يكون للوظيفة حد أدنى ، منذ ذلك الحين ذ(0) = 0 وللجميع x≠ 0ذ > 0.
- يترك x< x
0. ثم ج< x
0 و و "(ج)> 0.
لهذا و "(ج) (x-x 0)<
0 وبالتالي ،
و (س) - و (س 0 )< 0 ، أي و (خ)< f(x 0 ).
- يترك x> x 0. ثم ج> س 0 و و "(ج)< 0. وسائل و "(ج) (x-x 0)< 0. لهذا و (س) - و (س 0 ) <0,т.е.و (خ)< و (x 0 ) .
- أوجد نطاق الدالة و (خ).
- أوجد المشتق الأول للدالة و "(خ).
- تحديد النقاط الحرجة لهذا:
- أوجد الجذور الحقيقية للمعادلة و "(خ)=0;
- تجد كل القيم xالذي تحته المشتق و "(خ)غير موجود.
- أوجد إشارة المشتق إلى يسار ويمين النقطة الحرجة. نظرًا لأن علامة المشتق تظل ثابتة بين نقطتين حرجتين ، يكفي تحديد علامة المشتق في أي نقطة واحدة إلى اليسار وعند نقطة واحدة إلى يمين النقطة الحرجة.
- احسب قيمة الدالة عند النقاط القصوى.
- أوجد جميع النقاط الحرجة للدالة في الفترة ( أ ، ب) وحساب قيم الدالة في هذه النقاط.
- احسب قيم الدالة في نهايات المقطع من أجل س = أ ، س = ب.
- من بين جميع القيم التي تم الحصول عليها ، اختر الأكبر والأصغر.

الدالة ليس لها مشتق في x= 0 ، لأنه يذهب إلى اللانهاية متى x= 0. لكن في هذه المرحلة ، يكون للدالة حد أقصى.
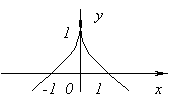
الدالة ليس لها مشتق في x= 0 لأن ![]() في x→ 0. في هذه المرحلة ، ليس للوظيفة حد أقصى أو حد أدنى. حقًا، و (خ)= 0 وفي x<0و (خ)<0, а при x>0و (خ)>0.
في x→ 0. في هذه المرحلة ، ليس للوظيفة حد أقصى أو حد أدنى. حقًا، و (خ)= 0 وفي x<0و (خ)<0, а при x>0و (خ)>0.

وهكذا ، من الأمثلة المعطاة والنظرية المصاغة ، من الواضح أن الوظيفة يمكن أن يكون لها حد أقصى فقط في حالتين: 1) عند النقاط التي يوجد فيها المشتق ويساوي الصفر ؛ 2) عند النقطة التي لا يوجد فيها المشتق.
ومع ذلك ، إذا في مرحلة ما x 0 نحن نعلم ذلك و "(x 0 ) = 0 ، فلا يمكن استنتاج ذلك من هذا عند هذه النقطة x 0 الوظيفة لها حد أقصى.
فمثلا. ![]() .
.

لكن النقطة x= 0 ليست نقطة قصوى ، حيث توجد قيم الوظيفة على يسار هذه النقطة أسفل المحور ثوروما فوق على اليمين.
تسمى قيم الحجة من مجال الوظيفة ، والتي يختفي فيها مشتق الوظيفة أو لا يوجد لها ، نقاط حرجة.
يترتب على ما سبق أن النقاط القصوى لوظيفة ما هي من بين النقاط الحرجة ، ومع ذلك ، ليست كل نقطة حرجة هي النقطة القصوى. لذلك ، للعثور على الحد الأقصى للدالة ، تحتاج إلى إيجاد جميع النقاط الحرجة للدالة ، ثم فحص كل نقطة من هذه النقاط بشكل منفصل من أجل الحد الأقصى والحد الأدنى. لهذا ، تخدم النظرية التالية.
النظرية 2. (شرط كاف لوجود حد أقصى.)دع الوظيفة تكون مستمرة في بعض الفترات التي تحتوي على النقطة الحرجة x 0 ، ويمكن اشتقاقه في جميع نقاط هذه الفترة (باستثناء ، ربما ، النقطة نفسها x 0). إذا ، عند المرور من اليسار إلى اليمين عبر هذه النقطة ، يتغير المشتق من موجب إلى سالب ، ثم عند هذه النقطة x = x 0 الوظيفة لها حد أقصى. إذا ، عند المرور x 0 من اليسار إلى اليمين ، يتغير المشتق من سالب إلى موجب ، ثم يكون للدالة حد أدنى عند هذه النقطة.
وهكذا ، إذا
دليل - إثبات. دعونا نفترض أولاً ذلك عند المرور x 0 ، يتغير المشتق من زائد إلى ناقص ، أي للجميع xقريب من النقطة x 0 و "(خ)> 0 من أجل x< x 0 , و "(خ)< 0 من أجل x> x 0. دعونا نطبق نظرية لاغرانج على الفرق و (س) - و (س 0 ) = f "(c) (x- x 0) أين جيقع بين xو x 0 .
وهكذا ، لجميع القيم xقريبة بما فيه الكفاية ل x 0 و (خ)< و (x 0 ) . وهذا يعني ذلك عند هذه النقطة x 0 الوظيفة لها حد أقصى.
تم إثبات الجزء الثاني من نظرية الحد الأدنى بالمثل.
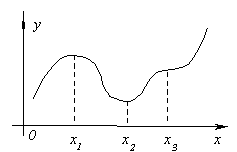
دعونا نوضح معنى هذه النظرية في الشكل. يترك و "(x 1 ) = 0 ولأي س ،قريبة بما فيه الكفاية ل x 1 ، عدم المساواة
و "(خ)< 0 في x< x 1 , و "(خ)> 0 في x> x 1 .
ثم إلى يسار النقطة x 1 تتزايد الدالة وتتناقص على اليمين ، لذلك متى x = xتنتقل وظيفة 1 من الزيادة إلى النقصان ، أي أن لها حدًا أقصى.
وبالمثل ، يمكن للمرء أن ينظر في النقاط x 2 و x 3 .

من الناحية التخطيطية ، يمكن تصوير كل ما سبق في الصورة:
قاعدة دراسة الدالة y = f (x) للنقطة القصوى
أمثلة. استكشف الوظائف للحد الأدنى والأقصى.
أعظم وأقل قيمة للوظيفة على التقاطع
الاكبرقيمة دالة في مقطع هي الأكبر بين جميع قيمها في هذا المقطع ، و الأقلهي أصغر قيمها.
ضع في اعتبارك الوظيفة ص = و (س)مستمر على القطعة [ أ ، ب]. كما هو معروف ، تصل هذه الوظيفة إلى قيمها القصوى والدنيا ، إما على حدود المقطع أو داخله. إذا تم الوصول إلى الحد الأقصى أو الحد الأدنى لقيمة الوظيفة عند النقطة الداخلية للمقطع ، فإن هذه القيمة هي الحد الأقصى أو الحد الأدنى للوظيفة ، أي يتم الوصول إليها في النقاط الحرجة.
وهكذا ، نحصل على ما يلي قاعدة البحث عن أكبر وأصغر قيم دالة في المقطع [ أ ، ب] :
الزيادة والنقصان والدالة القصوى
يعد العثور على فترات الزيادة والنقصان والنقصان القصوى لوظيفة ما مهمة مستقلة وجزءًا مهمًا من المهام الأخرى ، على وجه الخصوص ، دراسة كاملة الوظائف. يتم تقديم المعلومات الأولية حول الزيادة والنقصان والنقصان الأقصى للوظيفة في الفصل النظري في المشتق، والتي أوصي بها بشدة للدراسة الأولية (أو التكرار)- أيضًا لسبب أن المادة التالية مبنية على للغاية جوهر المشتقكونه استمرارًا متناغمًا لهذه المقالة. على الرغم من أنه إذا كان الوقت ينفد ، فمن الممكن أيضًا العمل بشكل رسمي بحت من أمثلة درس اليوم.
واليوم هناك روح إجماع نادرة في الهواء ، ويمكنني أن أشعر بشكل مباشر أن كل الحاضرين يحترقون بالرغبة تعلم كيفية استكشاف دالة باستخدام مشتق. لذلك ، تظهر المصطلحات الأبدية الجيدة والمعقولة على الفور على شاشات أجهزة العرض الخاصة بك.
لاجل ماذا؟ أحد أكثر الأسباب العملية هو: لتوضيح ما هو مطلوب منك بشكل عام في مهمة معينة!
رتابة الوظيفة. نقاط Extremum والوظيفة القصوى
دعنا نفكر في بعض الوظائف. بشكل مبسط ، نحن نفترض ذلك مستمرعلى خط الأعداد بالكامل:

فقط في حالة ما ، سنتخلص فورًا من الأوهام المحتملة ، خاصةً لأولئك القراء الذين تعرفوا مؤخرًا فترات ثبات الإشارة للوظيفة. الآن نحن غير مهتم، كيف يقع الرسم البياني للوظيفة بالنسبة للمحور (أعلاه ، أدناه ، حيث يتقاطع مع المحور). للإقناع ، امسح المحاور ذهنيًا واترك رسمًا بيانيًا واحدًا. لأن المصلحة فيه.
دور يزيدفي فترة إذا كانت المتباينة صحيحة لأي نقطتين من هذه الفترة مرتبطة بالعلاقة. أي أن القيمة الأكبر للوسيطة تتوافق مع قيمة أكبر للدالة ، ويمتد الرسم البياني الخاص بها "من أسفل إلى أعلى". تنمو وظيفة العرض التوضيحي خلال الفترة الزمنية.
وبالمثل ، فإن الوظيفة تناقصفي فترة ما إذا كانت هناك نقطتان من هذه الفترة ، بحيث تكون المتباينة صحيحة. أي أن القيمة الأكبر للوسيطة تتوافق مع قيمة أصغر للدالة ، ويمتد الرسم البياني الخاص بها "من أعلى إلى أسفل". الدالة تتناقص خلال الفترات ![]() .
.
إذا كانت الدالة تتزايد أو تتناقص خلال فترة ما ، فيتم استدعاؤها رتابة تمامافي هذه الفترة. ما هي الرتابة؟ خذها حرفيا - رتابة.
من الممكن أيضا تحديد غير متناقصالوظيفة (حالة استرخاء في التعريف الأول) و غير متزايدالوظيفة (الحالة المخففة في التعريف الثاني). تسمى الوظيفة غير المتناقصة أو غير المتزايدة على فترة زمنية بوظيفة رتيبة في فترة زمنية معينة (الرتابة الصارمة هي حالة خاصة من الرتابة "العادلة").
تنظر النظرية أيضًا في مناهج أخرى لتحديد الزيادة / النقصان في الوظيفة ، بما في ذلك على فترات نصفية ، ومقاطع ، ولكن من أجل عدم صب الزيت أو الزيت على رأسك ، فإننا نتفق على العمل بفواصل زمنية مفتوحة مع تعريفات قاطعة - هذا أوضح ، ولحل العديد من المشكلات العملية يكفي تمامًا.
في هذا الطريق، في مقالاتي ، ستختفي دائمًا عبارة "رتابة الوظيفة" فتراترتابة صارمة(زيادة صارمة أو نقصان صارم في الوظيفة).
حي بوينت. كلمات يتفرق بعدها الطلاب أينما استطاعوا ويختبئون في رعب في الزوايا. ... على الرغم من بعد آخر حدود كوشيربما لا يختبئون بعد الآن ، لكنهم يرتجفون قليلاً =) لا تقلق ، الآن لن تكون هناك أدلة على نظريات التحليل الرياضي - كنت بحاجة إلى الحي لصياغة التعريفات بشكل أكثر صرامة النقاط القصوى. نحن نتذكر:
نقطة الجوارقم بتسمية الفاصل الزمني الذي يحتوي على نقطة معينة ، بينما من أجل الراحة ، يُفترض غالبًا أن يكون الفاصل الزمني متماثلًا. على سبيل المثال ، نقطة وجوارها القياسي:
التعريفات الأساسية:
النقطة تسمى نقطة قصوى صارمة، إذا موجودحيها ، للجميعقيم منها ، باستثناء النقطة نفسها ، تتحقق عدم المساواة. في مثالنا الخاص ، هذه نقطة.
النقطة تسمى الحد الأدنى الصارم للنقطة، إذا موجودحيها ، للجميعقيم منها ، باستثناء النقطة نفسها ، تتحقق عدم المساواة. في الرسم - أشر "أ".
ملحوظة : اشتراط أن يكون الحي متماثلًا ليس ضروريًا على الإطلاق. بالإضافة إلى ذلك ، من المهم حقيقة الوجودالحي (وإن كان صغيرًا ، وحتى مجهريًا) يفي بالشروط المحددة
تسمى النقاط نقاط صارمة صارمةأو ببساطة النقاط القصوىالمهام. أي أنه مصطلح معمم للحد الأقصى من النقاط والحد الأدنى من النقاط.
كيف نفهم كلمة "المتطرفة"؟ نعم ، بشكل مباشر مثل الرتابة. النقاط المتطرفة للمركبة الدوارة.
كما في حالة الرتابة ، توجد في النظرية وحتى أكثر الافتراضات غير الصارمة شيوعًا (والتي بموجبها ، بالطبع ، تندرج القضايا الصارمة المدروسة!):
النقطة تسمى أقصى نقطة، إذا موجودمحيطها ، مثل هذا للجميع
النقطة تسمى الحد الأدنى من النقاط، إذا موجودمحيطها ، مثل هذا للجميعقيم هذا الحي ، تحمل عدم المساواة.
لاحظ أنه وفقًا للتعريفين الأخيرين ، فإن أي نقطة لدالة ثابتة (أو "منطقة مسطحة" لبعض الوظائف) تعتبر نقطة قصوى ونقطة دنيا! بالمناسبة ، الوظيفة غير متزايدة وغير متناقصة ، أي رتيبة. ومع ذلك ، نترك هذه الحجج للمنظرين ، حيث أننا في الممارسة تقريبًا نفكر في "التلال" و "الأجوف" التقليدية (انظر الرسم) مع "ملك التل" أو "أميرة المستنقعات" الفريد. كتنوع ، يحدث نقطة، موجهة لأعلى أو لأسفل ، على سبيل المثال ، الحد الأدنى من الوظيفة عند النقطة.
أوه ، والحديث عن الملوك:
- يسمى المعنى أقصىالمهام؛
- يسمى المعنى الحد الأدنىالمهام.
اسم شائع - المتطرفينالمهام.
من فضلك كن حذرا مع كلماتك!
النقاط القصوىهي قيم "س".
النهايات- قيم "اللعبة".
! ملحوظة : في بعض الأحيان تشير المصطلحات المدرجة إلى النقاط "x-y" التي تقع مباشرة على الرسم البياني للوظيفة.
كم عدد القيم القصوى التي يمكن أن تحتويها الوظيفة؟
لا شيء ، 1 ، 2 ، 3 ، ... إلخ. إلى ما لا نهاية. على سبيل المثال ، يحتوي الجيب على عدد لا حصر له من القيم الدنيا والحد الأقصى.
مهم!مصطلح "الوظيفة القصوى" لم تكن متطابقةمصطلح "القيمة القصوى للدالة". من السهل أن نرى أن القيمة القصوى هي فقط في الجوار المحلي ، وهناك "رفاق أكثر فجأة" في أعلى اليسار. وبالمثل ، فإن "الحد الأدنى للدالة" ليس هو نفسه "الحد الأدنى لقيمة الوظيفة" ، وفي الرسم يمكننا أن نرى أن القيمة هي الحد الأدنى فقط في منطقة معينة. في هذا الصدد ، تسمى النقاط المتطرفة أيضًا نقاط الطرفية المحلية، والقيمة القصوى التطرف المحلي. يمشون ويتجولون و عالميالاخوة. إذن ، أي قطع مكافئ يقع في قمته الحد الأدنى العالميأو الحد الأقصى العالمي. علاوة على ذلك ، لن أفرق بين أنواع التطرف ، ويتم التعبير عن التفسير أكثر للأغراض التعليمية العامة - الصفات الإضافية "محلي" / "عالمي" لا ينبغي أن تؤخذ على حين غرة.
دعنا نلخص استطراغنا القصير في النظرية بلقطة تحكم: ما الذي تعنيه مهمة "إيجاد فترات من الرتابة والنقاط القصوى لوظيفة ما"؟
تطالب الصياغة بالعثور على:
- فترات الزيادة / النقصان في الوظيفة (تظهر غير متناقصة ، غير متزايدة في كثير من الأحيان أقل) ؛
- الحد الأقصى للنقاط و / أو الحد الأدنى من النقاط (إن وجد). حسنًا ، من الأفضل العثور على الحد الأدنى / الحد الأقصى بأنفسهم من الفشل ؛-)
كيف تحدد كل هذا؟بمساعدة دالة مشتقة!
كيفية إيجاد فترات الزيادة والنقصان
النقاط القصوى والدالة القصوى؟
العديد من القواعد ، في الواقع ، معروفة بالفعل ومفهومة من درس حول معنى المشتق.
مشتق الظل ![]() يحمل الخبر السار بأن الوظيفة تتزايد طوال الوقت المجالات.
يحمل الخبر السار بأن الوظيفة تتزايد طوال الوقت المجالات.
مع ظل التمام ومشتقاته ![]() الوضع هو عكس ذلك تماما.
الوضع هو عكس ذلك تماما.
ينمو القوس على الفترة - المشتق موجب هنا: ![]() .
.
على سبيل المثال ، يتم تعريف الوظيفة ولكن لا يمكن تمييزها. ومع ذلك ، عند النقطة الحرجة ، يوجد مشتق يمين وظل يمين ، وعلى الحافة الأخرى ، يوجد نظائرهما اليسرى.
أعتقد أنه لن يكون من الصعب عليك تنفيذ تفكير مماثل لجيب التمام القوسي ومشتقاته.
كل هذه الحالات ، وكثير منها المشتقات المجدولة، أذكرك ، اتبع مباشرة من تعريفات المشتق.
لماذا نستكشف وظيفة بمشتق؟
للحصول على فكرة أفضل عن شكل الرسم البياني لهذه الوظيفة: حيث يذهب "من الأسفل إلى الأعلى" ، حيث يذهب "من الأعلى إلى الأسفل" ، حيث يصل إلى أدنى المستويات (على كل حال). ليست كل الوظائف بهذه البساطة - في معظم الحالات ، ليس لدينا عمومًا أدنى فكرة عن الرسم البياني لوظيفة معينة.
حان الوقت للانتقال إلى أمثلة أكثر أهمية والتفكير فيها خوارزمية لإيجاد فترات الرتابة والنهايات القصوى للدالة:
مثال 1
أوجد فترات الزيادة / النقصان والنقاط القصوى للدالة
![]()
المحلول:
1) الخطوة الأولى هي إيجاد نطاق الوظيفة، وكذلك لاحظ نقاط التوقف (إن وجدت). في هذه الحالة ، تكون الوظيفة مستمرة على الخط الحقيقي بأكمله ، وهذا الإجراء رسمي إلى حد ما. لكن في بعض الحالات ، تندلع هنا عواطف خطيرة ، لذلك دعونا نتعامل مع الفقرة دون إهمال.
2) النقطة الثانية من الخوارزمية مستحقة
شرط ضروري لأقصى حد:
إذا كان هناك حد أقصى عند هذه النقطة ، فإما أن القيمة غير موجودة.
حائر من النهاية؟ أقصى حد للوظيفة "modulo x" .
شرط ضروري ، ولكن ليس كافي، والعكس ليس صحيحًا دائمًا. لذلك ، لا يتبع المساواة بعد أن تصل الوظيفة إلى الحد الأقصى أو الحد الأدنى عند هذه النقطة. تم بالفعل إضاءة مثال كلاسيكي أعلاه - هذا قطع مكافئ مكعب ونقطته الحرجة.
ولكن مهما كان الأمر ، فإن الشرط الضروري للنقطة القصوى يملي الحاجة إلى العثور على النقاط المشبوهة. للقيام بذلك ، أوجد المشتق وحل المعادلة:
في بداية المقال الأول حول الرسوم البيانية للوظائفأخبرتك كيف تبني بسرعة القطع المكافئ باستخدام مثال ![]() : "... نأخذ المشتق الأول ونعادله بالصفر: ... إذن ، حل معادلتنا: - عند هذه النقطة يقع الجزء العلوي من القطع المكافئ ...". الآن ، أعتقد أن الجميع يفهم سبب وجود الجزء العلوي من القطع المكافئ بالضبط عند هذه النقطة =) بشكل عام ، يجب أن نبدأ بمثال مشابه هنا ، لكنه بسيط جدًا (حتى بالنسبة لإبريق الشاي). بالإضافة إلى ذلك ، يوجد تناظرية في نهاية الدرس حول دالة مشتقة. لذلك دعونا نرفع المستوى:
: "... نأخذ المشتق الأول ونعادله بالصفر: ... إذن ، حل معادلتنا: - عند هذه النقطة يقع الجزء العلوي من القطع المكافئ ...". الآن ، أعتقد أن الجميع يفهم سبب وجود الجزء العلوي من القطع المكافئ بالضبط عند هذه النقطة =) بشكل عام ، يجب أن نبدأ بمثال مشابه هنا ، لكنه بسيط جدًا (حتى بالنسبة لإبريق الشاي). بالإضافة إلى ذلك ، يوجد تناظرية في نهاية الدرس حول دالة مشتقة. لذلك دعونا نرفع المستوى:
مثال 2
أوجد فترات الرتابة والنهايات القصوى للدالة
هذا مثال على "افعل ذلك بنفسك". حل كامل وعينة تقريبية نهائية للمشكلة في نهاية الدرس.
لقد حان الوقت الذي طال انتظاره من الاجتماع مع الوظائف المنطقية الكسرية:
مثال 3
اكتشف دالة باستخدام المشتق الأول
انتبه إلى كيف يمكن إعادة صياغة نفس المهمة بشكل متنوع.
المحلول:
1) تعاني الوظيفة من فواصل لا نهائية عند النقاط.
2) نكتشف النقاط الحرجة. لنجد المشتق الأول ونعادله بالصفر: 
لنحل المعادلة. الكسر يساوي صفرًا عندما يكون بسطه صفرًا:
وهكذا نحصل على ثلاث نقاط حرجة: ![]()
3) ضع جانبا جميع النقاط المكتشفة على خط الأعداد و طريقة الفاصلتحديد علامات المشتقات:
أذكرك أنك بحاجة إلى أخذ نقطة معينة من الفترة ، وحساب قيمة المشتق فيها ![]() وتحديد علامته. من الأكثر ربحية عدم العد ، ولكن "التقدير" لفظيًا. خذ ، على سبيل المثال ، نقطة تنتمي إلى الفترة ، وقم بإجراء الاستبدال:
وتحديد علامته. من الأكثر ربحية عدم العد ، ولكن "التقدير" لفظيًا. خذ ، على سبيل المثال ، نقطة تنتمي إلى الفترة ، وقم بإجراء الاستبدال: ![]() .
. 
اثنان "زائد" وواحد "ناقص" يعطي "سالب" ، مما يعني أن المشتقة سالبة في الفترة بأكملها.
يجب تنفيذ الإجراء ، كما تفهم ، لكل فترة من الفترات الست. بالمناسبة ، لاحظ أن عامل البسط والمقام موجبان تمامًا لأي نقطة في أي فترة ، مما يبسط المهمة إلى حد كبير.
لذلك ، أخبرنا المشتق أن الوظيفة نفسها تزيد بمقدار ![]() ويقل بنسبة. من الملائم ربط فترات زمنية من نفس النوع برمز الاتحاد.
ويقل بنسبة. من الملائم ربط فترات زمنية من نفس النوع برمز الاتحاد.
عند النقطة تصل الوظيفة إلى الحد الأقصى:
عند هذه النقطة تصل الوظيفة إلى الحد الأدنى لها: ![]()
فكر في سبب عدم قدرتك على إعادة حساب القيمة الثانية ؛-)
عند المرور عبر نقطة ، لا يغير المشتق الإشارة ، وبالتالي فإن الوظيفة ليس لها حد كبير هناك - إنها تنخفض وتظل في تناقص.
! دعنا نكرر نقطة مهمة: النقاط لا تعتبر حرجة - لها وظيفة لم يحدد. تبعا لذلك ، هنا لا يمكن أن يكون الطرفان من حيث المبدأ(حتى لو تغير المشتق علامة).
إجابه: تزيد الوظيفة بمقدار ![]() ويقل عند النقطة التي يتم الوصول فيها إلى الحد الأقصى للوظيفة:
ويقل عند النقطة التي يتم الوصول فيها إلى الحد الأقصى للوظيفة: ![]() ، وعند النقطة - الحد الأدنى:.
، وعند النقطة - الحد الأدنى:.
معرفة فترات الرتابة والنهايات القصوى ، إلى جانب المنشأة الخطوط المقاربةيعطي فكرة جيدة جدًا عن مظهر الرسم البياني للوظيفة. يمكن للشخص العادي أن يحدد شفهيًا أن الرسم البياني للوظيفة يحتوي على خطين مقاربين عموديين وخط مقارب مائل. هنا بطلنا: 
حاول مرة أخرى ربط نتائج الدراسة بالرسم البياني لهذه الوظيفة.
لا يوجد حد أقصى في النقطة الحرجة ، ولكن هناك انعطاف منحنى(والذي ، كقاعدة عامة ، يحدث في حالات مماثلة).
مثال 4
أوجد القيمة القصوى لدالة
مثال 5
أوجد فترات الرتابة ، والحدود القصوى والدنيا للدالة
... مجرد نوع من عطلة X-in-a-cube تظهر اليوم ....
Soooo ، من هناك في المعرض عرض للشرب من أجل هذا؟ =)
كل مهمة لها الفروق الدقيقة الموضوعية والفنية الخاصة بها ، والتي يتم التعليق عليها في نهاية الدرس.
الوظائف ، ليس من الضروري على الإطلاق معرفة وجود المشتقات الأولى والثانية وفهم معناها المادي. تحتاج أولاً إلى فهم ما يلي:
- تعمل القيم القصوى للدالة على زيادة قيمة الوظيفة إلى الحد الأقصى أو ، على العكس من ذلك ، تقليلها في حي صغير عشوائيًا ؛
- عند النقطة القصوى لا ينبغي أن يكون هناك انقطاع في الوظيفة.
والآن نفس الشيء ، فقط بعبارات بسيطة. انظر إلى طرف قلم حبر جاف. إذا تم وضع القلم عموديًا ، مع نهاية الكتابة ، فسيكون منتصف الكرة هو أقصى نقطة - أعلى نقطة. في هذه الحالة نتحدث عن الحد الأقصى. الآن ، إذا قمت بقلب القلم بنهاية الكتابة لأسفل ، فسيكون هناك بالفعل حد أدنى من الوظيفة في منتصف الكرة. بمساعدة الشكل الموضح هنا ، يمكنك تخيل التلاعبات المدرجة في قلم رصاص القرطاسية. لذا ، فإن القيم القصوى للدالة هي دائمًا نقاط حرجة: الحد الأقصى أو الصغرى. يمكن أن يكون القسم المجاور من المخطط حادًا أو سلسًا بشكل تعسفي ، ولكن يجب أن يكون موجودًا على كلا الجانبين ، فقط في هذه الحالة تكون النقطة هي أقصى حد. إذا كان المخطط موجودًا على جانب واحد فقط ، فلن تكون هذه النقطة حدًا أقصى حتى إذا تم استيفاء الشروط القصوى على أحد جانبيها. الآن دعونا ندرس القيم القصوى للدالة من وجهة نظر علمية. من أجل اعتبار نقطة حدًا أقصى ، من الضروري والكافي أن:
- المشتق الأول كان يساوي صفرًا أو لم يكن موجودًا عند النقطة ؛
- أول علامة تغييرات مشتقة في هذه المرحلة.

يتم تفسير الشرط بشكل مختلف إلى حد ما عن وجهة نظر المشتقات ذات الرتبة الأعلى: بالنسبة لوظيفة قابلة للتفاضل عند نقطة ما ، يكفي أن يكون هناك مشتق فردي لا يساوي الصفر ، في حين أن جميع المشتقات ذات الرتبة الأدنى يجب أن تكون موجودة وأن تكون يساوي الصفر. هذا هو أبسط تفسير للنظريات من الكتب المدرسية ، لكن بالنسبة لمعظم الناس العاديين ، يجدر شرح هذه النقطة بمثال. الأساس هو قطع مكافئ عادي. قم بإجراء حجز على الفور ، عند نقطة الصفر يكون الحد الأدنى. مجرد القليل من الرياضيات:
- المشتق الأول (X 2) | = 2X ، لصفر نقطة 2X = 0 ؛
- المشتق الثاني (2X) | = 2 ، لصفر نقطة 2 = 2.

بهذه الطريقة البسيطة ، يتم توضيح الشروط التي تحدد الحدود القصوى للدالة لكل من المشتقات من الدرجة الأولى والمشتقات عالية الرتبة. يمكن أن نضيف إلى هذا أن المشتق الثاني هو نفس مشتق ترتيب فردي ، غير مساوٍ للصفر ، والذي تم ذكره أعلى قليلاً. عندما يتعلق الأمر بالدالة القصوى لدالة متغيرين ، يجب استيفاء الشروط لكلا الوسيطتين. عندما يحدث التعميم ، فإن المشتقات الجزئية تدخل حيز التنفيذ. أي أنه من الضروري وجود حد أقصى عند نقطة يكون فيها كلا المشتقين من الدرجة الأولى مساوياً للصفر ، أو أن أحدهما على الأقل غير موجود. من أجل كفاية وجود الحد الأقصى ، يتم التحقق من التعبير ، وهو الفرق بين ناتج المشتقات من الدرجة الثانية ومربع المشتق المختلط من الدرجة الثانية للوظيفة. إذا كان هذا التعبير أكبر من الصفر ، فهناك حد أقصى ، وإذا كان هناك تساوي للصفر ، فسيظل السؤال مفتوحًا ، وهناك حاجة إلى مزيد من البحث.