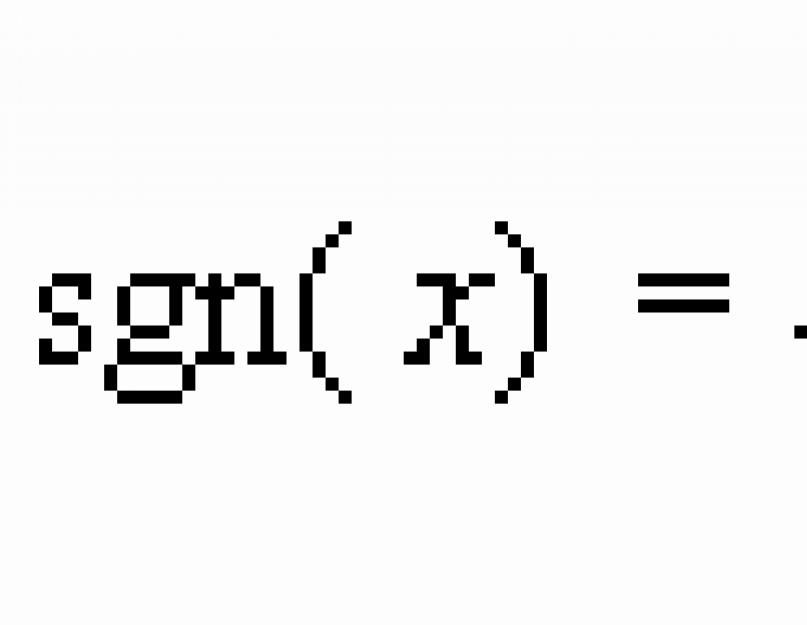في كثير من الأحيان ، عند حل المتباينات اللوغاريتمية ، توجد مشاكل ذات أساس متغير للوغاريتم. إذن ، عدم المساواة في الشكل

هو عدم المساواة المدرسة القياسية. كقاعدة عامة ، لحلها ، يتم استخدام الانتقال إلى مجموعة معادلة من الأنظمة:

عيب هذه الطريقة هو الحاجة إلى حل سبع متباينات ، بدون عد نظامين ومجموعة واحدة. حتى مع وجود دوال تربيعية معينة ، قد يتطلب حل السكان الكثير من الوقت.

يمكن اقتراح طريقة بديلة أقل استهلاكا للوقت لحل هذا التفاوت القياسي. للقيام بذلك ، نأخذ في الاعتبار النظرية التالية.

النظرية 1. دع دالة متزايدة مستمرة على مجموعة X. ثم في هذه المجموعة ستتزامن علامة زيادة الوظيفة مع علامة زيادة الوسيطة ، أي ، أين .

ملاحظة: إذا كانت دالة التناقص المستمر في المجموعة X ، إذن.

دعنا نعود إلى عدم المساواة. دعنا ننتقل إلى اللوغاريتم العشري (يمكنك الانتقال إلى أي قاعدة ثابتة أكبر من واحد).

يمكننا الآن استخدام النظرية ، مع ملاحظة زيادة الدوال في البسط وفي المقام. لذلك هذا صحيح

نتيجة لذلك ، يتم تقليل عدد العمليات الحسابية التي تؤدي إلى الإجابة بمقدار النصف تقريبًا ، مما يوفر ليس الوقت فحسب ، بل يسمح لك أيضًا باحتمالية ارتكاب أخطاء حسابية أقل وإهمالًا.

مثال 1

بالمقارنة مع (1) نجد , , .

بالمرور إلى (2) سيكون لدينا:

مثال 2

وبالمقارنة مع (1) نجد ، ،.

بالمرور إلى (2) سيكون لدينا:

مثال 3

بما أن الجانب الأيسر من المتباينة دالة متزايدة لـ و ، ثم يتم تعيين الإجابة.

يمكن توسيع مجموعة الأمثلة التي يمكن فيها تطبيق Terme 1 بسهولة إذا تم أخذ Terme 2 في الاعتبار.

دع على المجموعة Xيتم تحديد الوظائف ، وعلى هذا تعيين العلامات وتتزامن ، أي ، ثم سيكون ذلك عادلا.

مثال 4

مثال 5

باستخدام النهج القياسي ، يتم حل المثال وفقًا للمخطط: المنتج أقل من الصفر عندما تكون العوامل من علامات مختلفة. أولئك. نأخذ في الاعتبار مجموعة من نظامين من المتباينات حيث ، كما أشرنا في البداية ، تنقسم كل متباينة إلى سبعة أخرى.

إذا أخذنا في الاعتبار النظرية 2 ، فيمكن استبدال كل عامل ، مع الأخذ في الاعتبار (2) ، بوظيفة أخرى لها نفس العلامة في هذا المثال من O.D.Z.

تبين أن طريقة استبدال زيادة دالة بزيادة الوسيطة ، مع مراعاة النظرية 2 ، تكون ملائمة للغاية عند حل مشكلات استخدام C3 النموذجية.

مثال 6

مثال 7

. دعنا نشير. يحصل

. لاحظ أن الاستبدال يعني:. بالعودة إلى المعادلة ، نحصل عليها .

المثال 8

في النظريات التي نستخدمها ، لا توجد قيود على فئات الوظائف. في هذه المقالة ، كمثال ، تم تطبيق النظريات لحل المتباينات اللوغاريتمية. ستوضح الأمثلة القليلة التالية الوعد بأسلوب حل الأنواع الأخرى من عدم المساواة.

هل تعتقد أنه لا يزال هناك وقت قبل الامتحان ، وسيكون لديك وقت للاستعداد؟ ربما يكون الأمر كذلك. ولكن على أي حال ، كلما بدأ الطالب التدريب مبكرًا ، زاد نجاحه في اجتياز الاختبارات. قررنا اليوم تكريس مقال لعدم المساواة اللوغاريتمية. هذه إحدى المهام ، مما يعني فرصة للحصول على نقطة إضافية.

هل تعرف بالفعل ما هو اللوغاريتم (سجل)؟ نأمل ذلك حقًا. لكن حتى لو لم يكن لديك إجابة على هذا السؤال ، فهذه ليست مشكلة. من السهل جدًا فهم ماهية اللوغاريتم.

لماذا بالضبط 4؟ تحتاج إلى رفع الرقم 3 إلى مثل هذه القوة للحصول على 81. عندما تفهم المبدأ ، يمكنك المتابعة إلى حسابات أكثر تعقيدًا.

لقد مررت بعدم المساواة قبل بضع سنوات. ومنذ ذلك الحين ، تقابلهم باستمرار في الرياضيات. إذا كنت تواجه مشكلة في حل التفاوتات ، فراجع القسم المناسب.
الآن ، عندما نتعرف على المفاهيم بشكل منفصل ، سننتقل إلى دراستها بشكل عام.

أبسط متباينة لوغاريتمية.

أبسط المتباينات اللوغاريتمية لا تقتصر على هذا المثال ، هناك ثلاث أخرى ، فقط بعلامات مختلفة. لماذا هذا مطلوب؟ لفهم كيفية حل مشكلة عدم المساواة باللوغاريتمات بشكل أفضل. نقدم الآن مثالًا أكثر قابلية للتطبيق ، لا يزال بسيطًا للغاية ، نترك المتباينات اللوغاريتمية المعقدة لوقت لاحق.

كيف حلها؟ كل شيء يبدأ مع ODZ. يجب أن تعرف المزيد عنها إذا كنت تريد دائمًا حل أي عدم مساواة بسهولة.

ما هو ODZ؟ DPV للتباينات اللوغاريتمية

يشير الاختصار إلى المنطقة القيم المسموح بها. في مهام الامتحان ، تظهر هذه الصياغة غالبًا. DPV مفيد لك ليس فقط في حالة عدم المساواة اللوغاريتمية.

انظر مرة أخرى إلى المثال أعلاه. سننظر في ODZ بناءً عليها ، حتى تفهم المبدأ ، ولا يثير حل التفاوتات اللوغاريتمية أسئلة. يستنتج من تعريف اللوغاريتم أن 2x + 4 يجب أن تكون أكبر من الصفر. في حالتنا ، هذا يعني ما يلي.

يجب أن يكون هذا الرقم موجبًا حسب التعريف. حل المتباينة المعروضة أعلاه. يمكن القيام بذلك شفهيًا ، ومن الواضح هنا أن X لا يمكن أن تكون أقل من 2. سيكون حل المتباينة هو تعريف نطاق القيم المقبولة.
لننتقل الآن إلى حل أبسط متباينة لوغاريتمية.

نحن نتجاهل اللوغاريتمات نفسها من كلا الجزأين من عدم المساواة. ماذا بقي لنا نتيجة لذلك؟ عدم المساواة البسيطة.

من السهل حلها. يجب أن تكون X أكبر من -0.5. الآن نقوم بدمج القيمتين اللتين تم الحصول عليهما في النظام. هكذا،

ستكون هذه منطقة القيم المقبولة لعدم المساواة اللوغاريتمية المدروسة.

لماذا هو مطلوب على الإطلاق ODZ؟ هذه فرصة للتخلص من الإجابات غير الصحيحة والمستحيلة. إذا لم تكن الإجابة ضمن نطاق القيم المقبولة ، فإن الإجابة ببساطة لا معنى لها. هذا أمر يستحق التذكر لفترة طويلة ، لأنه في الاختبار غالبًا ما تكون هناك حاجة للبحث عن ODZ ، ولا يتعلق الأمر فقط بعدم المساواة اللوغاريتمية.

خوارزمية لحل عدم المساواة اللوغاريتمية

الحل يتكون من عدة خطوات. أولاً ، من الضروري إيجاد نطاق القيم المقبولة. ستكون هناك قيمتان في ODZ ، وقد اعتبرنا ذلك أعلاه. الخطوة التالية هي حل المتباينة نفسها. طرق الحل هي كما يلي:

• طريقة الاستبدال المضاعف
• تقسيم؛
• طريقة الترشيد.

اعتمادًا على الموقف ، يجب استخدام إحدى الطرق المذكورة أعلاه. دعنا ننتقل مباشرة إلى الحل. سنكشف عن الطريقة الأكثر شيوعًا المناسبة لحل مهام الاستخدام في جميع الحالات تقريبًا. بعد ذلك ، سننظر في طريقة التحلل. يمكن أن يساعدك إذا صادفت عدم مساواة "مخادع" بشكل خاص. إذن ، خوارزمية حل المتباينة اللوغاريتمية.

أمثلة الحل :

ليس عبثًا أننا أخذنا مثل هذه اللامساواة على وجه التحديد! انتبه إلى القاعدة. تذكر: إذا كانت أكبر من واحد ، تظل العلامة كما هي عند البحث عن نطاق القيم الصالحة ؛ خلاف ذلك ، يجب تغيير علامة عدم المساواة.

نتيجة لذلك ، نحصل على عدم المساواة:

نقدم الآن الجهه اليسرىإلى صيغة المعادلة التي تساوي الصفر. بدلاً من علامة "أقل من" ، نضع "يساوي" ، ونحل المعادلة. وهكذا ، سوف نجد ODZ. نأمل أن يكون مع حل من هذا القبيل معادلة بسيطةلن يكون لديك مشكلة. الإجابات هي -4 و -2. هذا ليس كل شئ. تحتاج إلى عرض هذه النقاط على الرسم البياني ، ووضع "+" و "-". ما الذي يجب القيام به من أجل هذا؟ عوّض بأرقام من المجالات في التعبير. عندما تكون القيم موجبة ، نضع "+" هناك.

إجابة: x لا يمكن أن يكون أكبر من -4 وأقل من -2.

لقد وجدنا نطاق القيم الصالحة للجانب الأيسر فقط ، والآن نحتاج إلى إيجاد نطاق القيم الصالحة للجانب الأيمن. هذا ليس أسهل بأي حال من الأحوال. الجواب: -2. نحن نتقاطع مع كلا المنطقتين المستقبلين.

والآن فقط نبدأ في حل المتباينة نفسها.

دعونا نبسطها قدر الإمكان لتسهيل اتخاذ القرار.

نستخدم طريقة الفاصل مرة أخرى في الحل. دعنا نتخطى العمليات الحسابية ، فكل شيء معه واضح بالفعل من المثال السابق. إجابة.

لكن هذه الطريقة مناسبة إذا كانت المتباينة اللوغاريتمية لها نفس الأسس.

يتضمن حل المعادلات اللوغاريتمية والمتباينات ذات الأسس المختلفة اختزالًا أوليًا لقاعدة واحدة. ثم استخدم الطريقة المذكورة أعلاه. لكن هناك المزيد حالة صعبة. اعتبر واحدة من أكثر أنواع معقدةعدم المساواة اللوغاريتمية.

المتباينات اللوغاريتمية ذات القاعدة المتغيرة

كيف نحل عدم المساواة بمثل هذه الخصائص؟ نعم ، ويمكن العثور على هذا في الامتحان. حل عدم المساواة بالطريقة التالية سيكون له أيضًا تأثير مفيد على العملية التعليمية. دعونا نلقي نظرة على المشكلة بالتفصيل. دعونا نضع النظرية جانبًا وننتقل مباشرة إلى الممارسة. لحل التفاوتات اللوغاريتمية ، يكفي أن تتعرف مرة واحدة على المثال.

لحل المتباينة اللوغاريتمية للصيغة المعروضة ، من الضروري تقليل الجانب الأيمن إلى اللوغاريتم الذي له نفس الأساس. المبدأ يشبه التحولات المكافئة. نتيجة لذلك ، ستبدو عدم المساواة على هذا النحو.

في الواقع ، يبقى إنشاء نظام من عدم المساواة بدون لوغاريتمات. باستخدام طريقة التبرير ، ننتقل إلى نظام مكافئ من عدم المساواة. ستفهم القاعدة نفسها عندما تستبدل القيم المناسبة وتتبع تغييراتها. سيكون للنظام عدم المساواة التالية.

باستخدام طريقة العقلنة عند حل المتباينات ، عليك أن تتذكر ما يلي: تحتاج إلى طرح واحد من الأساس ، يتم طرح x ، من خلال تعريف اللوغاريتم ، من كلا جزأي المتباينة (اليمين من اليسار) ، وهما يتم ضرب التعبيرات ووضعها تحت العلامة الأصلية بالنسبة للصفر.

يتم تنفيذ الحل الإضافي بطريقة الفاصل الزمني ، كل شيء بسيط هنا. من المهم بالنسبة لك فهم الاختلافات في طرق الحل ، ثم يبدأ كل شيء في العمل بسهولة.

في عدم المساواة اللوغاريتميةالعديد من الفروق الدقيقة. أبسطها سهل بما يكفي لحلها. كيف أجعلها بحيث تحل كل منها دون مشاكل؟ لقد تلقيت بالفعل جميع الإجابات في هذا المقال. الآن لديك تدريب طويل أمامك. تدرب باستمرار على حل المشكلات المختلفة داخل الامتحان وستكون قادرًا على الحصول على أعلى الدرجات. حظا سعيدا في عملك الصعب!

عدم المساواة اللوغاريتمية

في الدروس السابقة ، تعرفنا على المعادلات اللوغاريتمية والآن نعرف ماهيتها وكيفية حلها. وسيخصص درس اليوم لدراسة التفاوتات اللوغاريتمية. ما هي هذه المتباينات وما هو الفرق بين حل معادلة لوغاريتمية وعدم المساواة؟

المتباينات اللوغاريتمية هي متباينات لها متغير تحت علامة اللوغاريتم أو في قاعدته.

أو ، يمكن للمرء أيضًا أن يقول إن اللوغاريتمية المتباينة هي عدم مساواة تكون فيها قيمتها غير المعروفة ، كما في المعادلة اللوغاريتمية ، تحت علامة اللوغاريتم.

تبدو أبسط المتباينات اللوغاريتمية كما يلي:

حيث f (x) و g (x) هي بعض التعبيرات التي تعتمد على x.

لننظر إلى هذا باستخدام المثال التالي: f (x) = 1 + 2x + x2، g (x) = 3x − 1.

حل المتباينات اللوغاريتمية

قبل حل المتباينات اللوغاريتمية ، تجدر الإشارة إلى أنه عندما يتم حلها ، فإنها تكون متشابهة عدم المساواة الأسية، يسمى:

أولاً ، عند الانتقال من اللوغاريتمات إلى التعبيرات الموجودة تحت علامة اللوغاريتم ، نحتاج أيضًا إلى مقارنة أساس اللوغاريتم بواحد ؛

ثانيًا ، عند حل متباينة لوغاريتمية باستخدام تغيير المتغيرات ، نحتاج إلى حل المتباينات بالنسبة للتغيير حتى نحصل على أبسط متباينة.

لكننا نحن من أخذنا بعين الاعتبار اللحظات المماثلة لحل المتباينات اللوغاريتمية. الآن دعونا نلقي نظرة على اختلاف كبير إلى حد ما. أنا وأنت نعلم أن الوظيفة اللوغاريتمية لها مجال تعريف محدود ، لذلك عند الانتقال من اللوغاريتمات إلى التعبيرات التي تقع تحت علامة اللوغاريتم ، يجب أن تأخذ في الاعتبار نطاق القيم المقبولة (ODV).

أي أنه يجب ألا يغيب عن البال أنه عند حل معادلة لوغاريتمية ، يمكننا أولاً إيجاد جذور المعادلة ، ثم التحقق من هذا الحل. لكن حل المتباينة اللوغاريتمية لن يعمل بهذه الطريقة ، نظرًا لأن الانتقال من اللوغاريتمات إلى التعبيرات تحت علامة اللوغاريتم ، سيكون من الضروري كتابة ODZ للمتباينة.

بالإضافة إلى ذلك ، تجدر الإشارة إلى أن نظرية عدم المساواة تتكون من أرقام حقيقية موجبة و أرقام سالبة، وكذلك الرقم 0.

على سبيل المثال ، عندما يكون الرقم "a" موجبًا ، يجب استخدام الرمز التالي: a> 0. في هذه الحالة ، سيكون كل من مجموع هذه الأرقام ومنتجها موجبًا أيضًا.

يتمثل المبدأ الأساسي لحل أي متباينة في استبدالها بأبسط متباينة ، لكن الشيء الرئيسي هو أنها تعادل المتباينة المعطاة. علاوة على ذلك ، حصلنا أيضًا على متباينة واستبدلناها مرة أخرى بأخرى ذات شكل أبسط ، وهكذا.

لحل المتباينات باستخدام متغير ، عليك إيجاد جميع حلوله. إذا كان لاثنين من المتباينات نفس المتغير x ، فإن هذه المتباينات تكون متكافئة بشرط أن تكون حلولها متطابقة.

عند تنفيذ مهام لحل التفاوتات اللوغاريتمية ، من الضروري أن نتذكر أنه عندما تكون a> 1 ، تزداد الدالة اللوغاريتمية ، وعندما تكون 0< a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить.

طرق لحل المتباينات اللوغاريتمية

لنلقِ الآن نظرة على بعض الطرق التي تستخدم لحل المتباينات اللوغاريتمية. من أجل فهم واستيعاب أفضل ، سنحاول فهمها باستخدام أمثلة محددة.

نعلم أن أبسط متباينة لوغاريتمية لها الشكل التالي:

في عدم المساواة هذا ، V - هي واحدة من علامات عدم المساواة مثل:<,>أو ≤ أو ≥.

عندما يكون أساس هذا اللوغاريتم أكبر من واحد (أ> 1) ، مما يجعل الانتقال من اللوغاريتمات إلى التعبيرات تحت علامة اللوغاريتم ، ثم في هذا الإصدار يتم الاحتفاظ بعلامة عدم المساواة ، وستبدو عدم المساواة كما يلي:

وهو ما يعادل النظام التالي:

إذا كان أساس اللوغاريتم أكبر من صفر و أقل من واحد (0

هذا يعادل هذا النظام:

لنلق نظرة على مزيد من الأمثلة لحل أبسط المتباينات اللوغاريتمية الموضحة في الصورة أدناه:

حل الأمثلة

يمارس.دعنا نحاول حل هذه المتباينة:

قرار مجال القيم المقبولة.

لنحاول الآن ضرب جانبه الأيمن في:

دعونا نرى ما يمكننا القيام به:

الآن ، دعنا ننتقل إلى تحويل التعبيرات الفرعية. بما أن أساس اللوغاريتم هو 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный:

3x - 8> 16 ؛
3x> 24 ؛
x> 8.

ومن هذا فإن الفترة التي حصلنا عليها تنتمي بالكامل إلى ODZ وهي حل لمثل هذه المتباينة.

ها هي الإجابة التي حصلنا عليها:

ما هو المطلوب لحل التفاوتات اللوغاريتمية؟

الآن دعنا نحاول تحليل ما نحتاجه لحل المتباينات اللوغاريتمية بنجاح؟

أولاً ، ركز كل انتباهك وحاول ألا ترتكب أخطاءً عند إجراء التحولات الواردة في عدم المساواة هذه. أيضًا ، يجب أن نتذكر أنه عند حل مثل هذه التفاوتات ، من الضروري منع التوسعات والتضيقات في عدم المساواة في منطقة ODZ ، والتي يمكن أن تؤدي إلى فقدان أو الحصول على حلول دخيلة.

ثانيًا ، عند حل التفاوتات اللوغاريتمية ، تحتاج إلى تعلم التفكير المنطقي وفهم الفرق بين مفاهيم مثل نظام عدم المساواة ومجموعة من عدم المساواة ، بحيث يمكنك بسهولة اختيار الحلول لعدم المساواة ، مع الاسترشاد بالـ DHS.

ثالثًا ، من أجل حل مثل هذه التفاوتات بنجاح ، يجب على كل واحد منكم أن يعرف جيدًا جميع خصائص الوظائف الأولية وأن يفهم معناها بوضوح. لا تشمل هذه الوظائف اللوغاريتمية فحسب ، بل تشمل أيضًا العقلانية والقوة والمثلثية وما إلى ذلك ، في كلمة واحدة ، كل تلك التي درستها طوال الوقت. التعليمالجبر.

كما ترى ، بعد دراسة موضوع عدم المساواة اللوغاريتمية ، لا يوجد شيء صعب في حل هذه التفاوتات ، بشرط أن تكون منتبهًا ومثابرًا في تحقيق أهدافك. حتى لا توجد مشاكل في حل عدم المساواة ، تحتاج إلى التدريب قدر الإمكان ، وحل المهام المختلفة وفي نفس الوقت حفظ الطرق الرئيسية لحل مثل هذه التفاوتات وأنظمتها. مع الحلول غير الناجحة لعدم المساواة اللوغاريتمية ، يجب عليك تحليل أخطائك بعناية حتى لا تعود إليها مرة أخرى في المستقبل.

العمل في المنزل

لاستيعاب الموضوع بشكل أفضل وتوحيد المادة التي تمت تغطيتها ، قم بحل التفاوتات التالية:

تسمى المتباينة اللوغاريتمية إذا كانت تحتوي على دالة لوغاريتمية.

لا تختلف طرق حل المتباينات اللوغاريتمية عنها فيما عدا شيئين.

أولاً ، عند الانتقال من عدم المساواة اللوغاريتمية إلى عدم المساواة في الدوال اللوغاريتمية الفرعية ، يتبع ذلك اتبع علامة عدم المساواة الناتجة. إنه يخضع للقاعدة التالية.

إذا كانت قاعدة الدالة اللوغاريتمية أكبر من 1 دولار ، فعند الانتقال من المتباينة اللوغاريتمية إلى متباينة الدوال اللوغاريتمية الفرعية ، يتم الاحتفاظ بعلامة عدم المساواة ، وإذا كانت أقل من 1 دولار ، فعندها يتم عكسها.

ثانيًا ، حل أي متباينة هو فاصل زمني ، وبالتالي ، في نهاية حل عدم المساواة في الدوال اللوغاريتمية الفرعية ، من الضروري تكوين نظام من متراجعتين: المتباينة الأولى في هذا النظام ستكون عدم المساواة في الدوال اللوغاريتمية الفرعية ، والثاني سيكون الفاصل الزمني لمجال تعريف الدوال اللوغاريتمية المضمنة في المتباينة اللوغاريتمية.

يمارس.

لنحل المتباينات:

1. $ \ log_ (2) ((x + 3)) geq 3. $

$ D (ص): \ x + 3> 0. $

$ x \ in (-3؛ + \ infty) $

أساس اللوغاريتم هو $ 2> 1 $ ، لذلك لا تتغير العلامة. باستخدام تعريف اللوغاريتم ، نحصل على:

$ x + 3 \ geq 2 ^ (3) ، $

x $ في)