Vjerovatnoća događaja $A$ je omjer broja ishoda povoljnih za $A$ i broja svih jednako mogućih ishoda
$P(A)=(m)/(n)$, gdje je $n$ ukupan broj mogućih ishoda, a $m$ je broj ishoda koji favoriziraju $A$.
Vjerovatnoća događaja je broj iz segmenta $$
Taksi kompanija ima na raspolaganju 50$ automobila. 35$ od njih su crne, ostale su žute. Pronađite vjerovatnoću da žuti automobil stigne na nasumični poziv.
Pronađite broj žutih automobila:
Ukupno ima automobila od 50$, odnosno jedan od pedeset će doći na poziv. Postoji 15$ žutih automobila, stoga je vjerovatnoća dolaska žutog automobila $(15)/(50)=(3)/(10)=0,3$
Odgovor: 0,3$
Suprotni događaji
Za dva događaja se kaže da su suprotna ako su u datom ispitivanju nespojiva i jedan od njih se nužno dogodi. Vjerovatnoće suprotnih događaja su 1. Događaj suprotan događaju $A$ piše se $((A))↖(-)$.
$P(A)+P((A))↖(-)=1$
Nezavisni događaji
Dva događaja $A$ i $B$ nazivaju se nezavisnim ako vjerovatnoća pojave svakog od njih ne zavisi od toga da li se drugi događaj dogodio ili ne. Inače, događaji se nazivaju zavisni.
Verovatnoća proizvoda dva nezavisna događaja $A$ i $B$ jednaka je proizvodu ovih verovatnoća:
$P(A B)=P(A) P(B)$
Ivan Ivanovič je kupio dvije različite lutrije. Verovatnoća da prvi pobedi srećka, jednako je 0,15$. Vjerovatnoća da će drugi tiket pobijediti je 0,12 dolara. Ivan Ivanovič učestvuje u oba izvlačenja. Uz pretpostavku da se ždrijebovi vode nezavisno jedan od drugog, pronađite vjerovatnoću da Ivan Ivanovič pobijedi u oba izvlačenja.
Vjerovatnoća $P(A)$ - osvaja prvi tiket.
Verovatnoća $P(B)$ - osvaja drugi listić.
Događaji $A$ i $B$ su nezavisni događaji. To jest, da biste pronašli vjerovatnoću da će se oba događaja dogoditi, morate pronaći proizvod vjerovatnoća
$P(A B)=P(A) P(B)$
$P=0,15 0,12=0,018$
Odgovor: 0,018 dolara
Nekompatibilni događaji
Kaže se da su dva događaja $A$ i $B$ nekompatibilna ako nema ishoda koji favorizuju i događaj $A$ i događaj $B$. (Događaji koji se ne mogu dogoditi u isto vrijeme)
Verovatnoća zbira dva nekompatibilna događaja $A$ i $B$ jednaka je zbiru verovatnoća ovih događaja:
$P(A+B)=P(A)+P(B)$
Na ispitu iz algebre student dobije jedno pitanje od svih ispita. Vjerovatnoća da je ovo pitanje na temu " Kvadratne jednadžbe", jednako je 0,3$. Vjerovatnoća da je ovo pitanje na temu " Iracionalne jednadžbe", jednako je 0,18$. Nema pitanja vezanih za ove dvije teme u isto vrijeme. Odrediti vjerovatnoću da će student na ispitu dobiti pitanje o jednoj od ove dvije teme.
Ovi događaji se nazivaju nespojivim, jer će učenik dobiti pitanje ILI na temu „Kvadrikularne jednačine“, ILI na temu „Iracionalne jednačine“. Teme se ne mogu uhvatiti u isto vrijeme. Verovatnoća zbira dva nekompatibilna događaja $A$ i $B$ jednaka je zbiru verovatnoća ovih događaja:
$P(A+B)=P(A)+P(B)$
$P = 0,3 + 0,18 \u003d 0,48 $
Odgovor: 0,48 dolara
Zajednički događaji
Za dva događaja se kaže da su zajednička ako pojava jednog od njih ne isključuje pojavu drugog u istom ispitivanju. U suprotnom, događaji se nazivaju nekompatibilnim.
Verovatnoća zbira dva zajednička događaja $A$ i $B$ jednaka je zbiru verovatnoća ovih događaja minus verovatnoća njihovog proizvoda:
$P(A+B)=P(A)+P(B)-P(A B)$
U holu kina nalaze se dva identična aparata za kafu. Vjerovatnoća da će aparat ostati bez kafe do kraja dana je 0,6$. Vjerovatnoća da obje mašine ostanu bez kafe je 0,32$. Pronađite vjerovatnoću da će barem jednom od automata ostati bez kafe do kraja dana.
Označimo događaje, neka:
$A$ = kafa će završiti u prvoj mašini,
$B$ = kafa će završiti u drugoj mašini.
$A B =$ kafa će nestati u oba automata,
$A + B =$ kafa će nestati u najmanje jednom automatu.
Po konvenciji, $P(A) = P(B) = 0,6; P(A B) = 0,32 USD.
Događaji $A$ i $B$ su zajednički, vjerovatnoća zbira dva zajednička događaja jednaka je zbroju vjerovatnoća ovih događaja, umanjena za vjerovatnoću njihovog proizvoda:
$P(A + B) = P(A) + P(B) − P(A B) = 0,6 + 0,6 − 0,32 = 0,88 $
Vjerovatnoća. Zadaci profilnog ispita iz matematike.
Pripremio profesor matematike u MBOU "Licej br. 4", Ruzaevka
Ovchinnikova T.V.

Definicija vjerovatnoće
Vjerovatnoća događaji A nazivaju omjer broja m povoljni ishodi za ovaj događaj ukupan broj n svi podjednako mogući nekompatibilni događaji koji se mogu dogoditi kao rezultat jednog testa ili promatranja:
m
n
Neka k - broj bacanja novčića, zatim broj mogućih ishoda: n=2 k .
Neka k - broj bacanja kockica, zatim broj mogućih ishoda: n=6 k .

U slučajnom eksperimentu, simetrični novčić se baca dvaput. Nađite vjerovatnoću da će se glave pojaviti tačno jednom.
Rješenje.
Samo 4 opcije: about; oh oh; p p; p p; o .
Povoljno 2: about; R i R; o .
Vjerovatnoća je 2/4 = 1/2 = 0,5 .
Odgovor: 0,5.

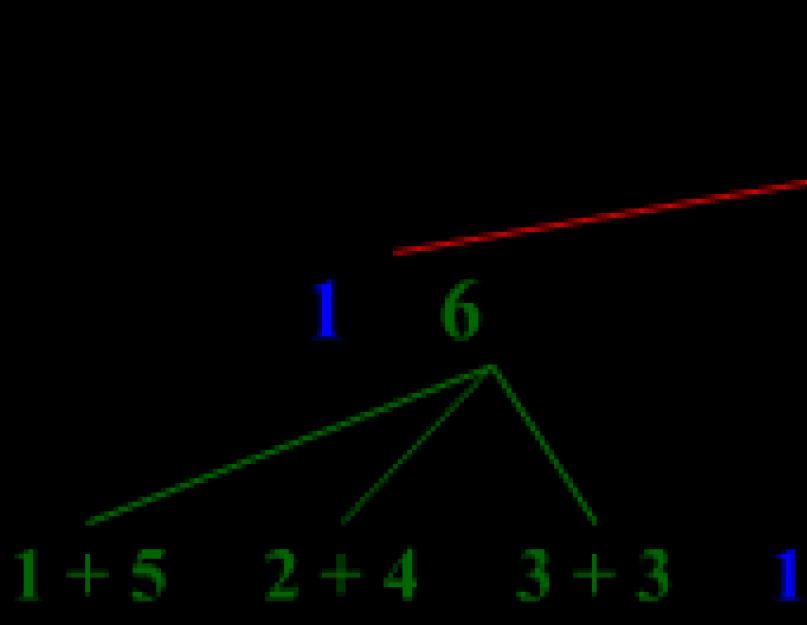
U slučajnom eksperimentu bacaju se dvije kockice. Pronađite vjerovatnoću da dobijete ukupno 8 bodova. Zaokružite rezultat na najbližu stotu.
Rješenje.
Kockice su kockice sa 6 strana. Prva kocka može baciti 1, 2, 3, 4, 5 ili 6 poena. Svaka opcija bodovanja odgovara 6 opcija za bodovanje na drugom kocku.
One. Ukupno razne opcije 6x6=36.
Opcije (ishodi eksperimenta) će biti sljedeće:
1; 1 1; 2 1; 3 1; 4 1; 5 1; 6
2; 1 2; 2 2; 3 2; 4 2; 5 2; 6
itd. ..............................
6; 1 6; 2 6; 3 6; 4 6; 5 6; 6
Izbrojimo broj ishoda (opcija) u kojima je zbir bodova dvije kocke 8.
2; 6 3; 5; 4; 4 5; 3 6; 2.
Samo 5 opcija.
Nađimo vjerovatnoću: 5/36 = 0,138 ≈ 0,14.
Odgovor: 0,14.

U kolekciji bioloških karata nalazi se ukupno 55 ulaznica, od kojih 11 sadrži pitanje o botanici. Pronađite vjerovatnoću da će student dobiti pitanje o botanici u slučajno odabranoj ispitnoj listi.
Rješenje:
Vjerovatnoća da će student dobiti pitanje o botanici u slučajno odabranom ispitnom listiću je 11/55 = 1/5 = 0,2.
Odgovor: 0.2.

Na prvenstvu u gimnastici učestvuje 20 atletičara: 8 iz Rusije, 7 iz SAD, ostali iz Kine. Redoslijed nastupa gimnastičarki određuje se žrijebom. Pronađite vjerovatnoću da je sportista koji se prvi takmiči iz Kine.
Rješenje.
Ukupno ima 20 sportista.
od kojih 20 - 8 - 7 = 5 sportista iz Kine.
Verovatnoća da će sportista koji se prvi takmiči biti iz Kine je 5/20 = 1/4 = 0,25.
Odgovor: 0,25.

Naučna konferencija se održava u 5 dana. Planirano je ukupno 75 izvještaja - prva tri dana po 17 izvještaja, ostali se ravnomjerno raspoređuju između četvrtog i petog dana. Redoslijed izvještaja određuje se žrijebom. Kolika je vjerovatnoća da će izvještaj profesora M. biti zakazan za posljednji dan konferencije?
Rješenje:
Predviđen je posljednji dan konferencije
(75 - 17 × 3) : 2 = 12 izvještaja.
Verovatnoća da će izveštaj profesora M. biti zakazan za poslednji dan konferencije je 12/75 = 4/25 = 0,16.
Odgovor: 0,16.

Prije početka prve runde prvenstva u badmintonu, žrijebom se nasumično dijele učesnici u parove. Ukupno na prvenstvu učestvuje 26 badmintonista, uključujući 10 učesnika iz Rusije, među kojima je i Ruslan Orlov. Naći vjerovatnoću da će u prvom kolu Ruslan Orlov igrati sa bilo kojim badmintonistom iz Rusije?
Rješenje:
Treba napomenuti da Ruslan Orlov mora igrati sa nekim badmintonistom iz Rusije. I sam Ruslan Orlov je takođe iz Rusije.
Verovatnoća da će u prvom kolu Ruslan Orlov igrati sa bilo kojim badmintonistom iz Rusije je 9/25 = 36/100 = 0,36.
Odgovor: 0,36.

Dasha baca dva puta kockice. Postigla je ukupno 8 poena. Pronađite vjerovatnoću da dobijete 2 pri prvom bacanju.
Rješenje.
Ukupno, dvije kocke bi trebale baciti 8 poena. To je moguće ako postoje sljedeće kombinacije:
Samo 5 opcija. Izbrojimo broj ishoda (opcija) u kojima su 2 boda pala pri prvom bacanju.
Ova opcija je 1.
Pronađite vjerovatnoću: 1/5 = 0,2.
Odgovor: 0.2.

Na Svjetskom prvenstvu učestvuje 20 ekipa. Uz pomoć ždrijeba, potrebno ih je podijeliti u pet grupa od po četiri tima. U kutiji se nalaze mešovite karte sa brojevima grupa:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5.
Kapiteni timova izvlače po jednu kartu. Kolika je vjerovatnoća da će ruski tim biti u trećoj grupi.
Rješenje:
Ukupno ima 20 ekipa, 5 grupa.
Svaka grupa ima 4 ekipe.
Dakle, ukupno smo dobili 20 ishoda, trebalo nam je 4, što znači da je vjerovatnoća da željeni ishod ispadne 4/20 = 0,2.
Odgovor: 0.2.

Dvije fabrike proizvode isto staklo za farove za automobile. Prva fabrika proizvodi 45% ovih naočara, druga - 55%. Prva fabrika proizvodi 3% neispravnih stakala, a druga 1%. Pronađite vjerovatnoću da će staklo slučajno kupljeno u trgovini biti neispravno.
Rješenje:
Verovatnoća da je staklo kupljeno u prvoj fabrici i da je neispravno:
R 1 = 0,45 0,03 = 0,0135.
Verovatnoća da je staklo kupljeno u drugoj fabrici i da je neispravno:
R 2 = 0,55 0,01 = 0,0055.
Dakle, prema formuli puna vjerovatnoća jednaka je vjerovatnoća da će staklo slučajno kupljeno u trgovini biti neispravno
p = p 1 + str 2 = 0,0135 + 0,0055 = 0,019.
Odgovor: 0,019.

Ako velemajstor A. igra bijelog, tada pobjeđuje velemajstora B. sa vjerovatnoćom 0,52. Ako A. igra crno, onda A. pobjeđuje B. sa vjerovatnoćom od 0,3.
Velemajstori A. i B. igraju dvije partije, au drugoj igri mijenjaju boju figura. Pronađite vjerovatnoću da A. pobijedi oba puta.
Rješenje:
Šanse za pobjedu u prvoj i drugoj utakmici su nezavisne jedna od druge. Vjerovatnoća nastanka nezavisnih događaja jednaka je proizvodu njihovih vjerovatnoća:
p = 0,52 0,3 = 0,156.
Odgovor: 0,156.

Biatlonac gađa pet puta u mete. Vjerovatnoća da jednim udarcem pogodite metu je 0,8. Pronađite vjerovatnoću da je biatlonac prva tri puta pogodio mete, a posljednja dva promašio. Zaokružite rezultat na najbližu stotu.
Rješenje:
Rezultat svakog sljedećeg udarca ne zavisi od prethodnih. Dakle, događaji „pogodan prvi hitac“, „pogodan drugi hitac“ itd. nezavisni.
Vjerovatnoća svakog pogotka je 0,8. Dakle, vjerovatnoća promašaja je 1 - 0,8 = 0,2.
1 šut: 0,8
2 šut: 0,8
3 šut: 0,8
4 šut: 0,2
5 šut: 0,2
Prema formuli za množenje vjerovatnoća nezavisnih događaja, nalazimo da je željena vjerovatnoća jednaka:
0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 = 0,02048 ≈ 0,02.
Odgovor: 0,02.

Prodavnica ima dva aparata za plaćanje. Svaki od njih može biti neispravan s vjerovatnoćom od 0,05, bez obzira na drugi automat. Pronađite vjerovatnoću da je barem jedan automat uslužan.
Rješenje:
Pronađite vjerovatnoću da su oba automata neispravna.
Ovi događaji su nezavisni, vjerovatnoća njihovog proizvoda jednaka je proizvodu vjerovatnoća ovih događaja:
0,05 0,05 = 0,0025.
Događaj koji se sastoji u činjenici da je barem jedan automat uslužan je suprotan.
Stoga je njegova vjerovatnoća
1 − 0,0025 = 0,9975.
Odgovor: 0,9975.

Kauboj Džon pogodi muvu u zid sa verovatnoćom od 0,9 ako puca iz revolvera. Ako John ispali neustreljeni revolver, pogodi muvu s vjerovatnoćom od 0,2. Na stolu je 10 revolvera, od kojih su samo 4 upucana. Kauboj Džon ugleda muvu na zidu, nasumično zgrabi prvi revolver na koji naiđe i puca u muvu. Pronađite vjerovatnoću da John promaši.
Rješenje:
Vjerovatnoća da će John promašiti ako zgrabi revolver za metak je:
0,4 (1 - 0,9) = 0,04
Verovatnoća da će Džon promašiti ako zgrabi neustreljeni revolver je:
0,6 (1 - 0,2) = 0,48
Ovi događaji su nekompatibilni, vjerovatnoća njihovog zbira jednaka je zbiru vjerovatnoća ovih događaja:
0,04 + 0,48 = 0,52.
Odgovor: 0,52.

Prilikom artiljerijske gađanja, automatski sistem gađa metu. Ako meta nije uništena, sistem ponovo puca. Pucnjevi se ponavljaju dok se meta ne uništi. Vjerovatnoća uništenja određene mete prvim hicem je 0,4, a svakim sljedećim 0,6. Koliko će hitaca biti potrebno da bi se osiguralo da je vjerovatnoća uništenja mete najmanje 0,98?
Rješenje:
Problem možete riješiti "djelima", računajući vjerovatnoću preživljavanja nakon niza uzastopnih promašaja:
P(1) = 0,6;
P(2) = P(1) 0,4 = 0,24;
P(3) = P(2) 0,4 = 0,096;
P(4) = P(3) 0,4 = 0,0384;
P(5) = P(4) 0,4 = 0,01536.
Zadnja vjerovatnoća je manja od 0,02, pa je dovoljno pet hitaca u metu.
Odgovor: 5.

U razredu je 26 ljudi, među njima i dva blizanca - Andrej i Sergej. Odeljenje je nasumično podijeljeno u dvije grupe od po 13 ljudi. Pronađite vjerovatnoću da će Andrej i Sergej biti u istoj grupi.
Rješenje:
Neka jedan od blizanaca bude u nekoj grupi.
Zajedno sa njim, u grupi će biti 12 ljudi od 25 preostalih drugova iz razreda.
Vjerovatnoća da će drugi blizanac biti među ovih 12 ljudi jednaka je
P=12:25=0,48.
Odgovor: 0,48.

Slika prikazuje lavirint. Pauk se uvlači u lavirint na tački "Ulaz". Pauk se ne može okrenuti i puzati nazad, stoga na svakom račvanju pauk bira jednu od staza kojom još nije puzao. Uz pretpostavku da je izbor daljeg puta čisto slučajan, odredite s kojom vjerovatnoćom će pauk doći na izlaz D.
Rješenje:
Na svakoj od četiri označene vile, pauk može izabrati ili put koji vodi do izlaza D ili drugu stazu sa vjerovatnoćom od 0,5. To su nezavisni događaji, vjerovatnoća njihovog proizvoda (pauk stiže do izlaza D) jednaka je proizvodu vjerovatnoća ovih događaja. Stoga je vjerovatnoća da se dođe do izlaza D (0,5) 4 = 0,0625.
Do danas je predstavljen u otvorenoj banci matematičkih zadataka USE (mathege.ru), čije se rješenje zasniva samo na jednoj formuli, koja je klasična definicija vjerovatnoće.
Najlakši način za razumijevanje formule je pomoću primjera.
Primjer 1 U košu se nalazi 9 crvenih i 3 plave loptice. Lopte se razlikuju samo po boji. Nasumično (bez gledanja) dobijamo jednu od njih. Kolika je vjerovatnoća da tako odabrana lopta bude plava?
Komentar. U problemima u teoriji vjerovatnoće, nešto se dešava (in ovaj slučaj naša akcija za izvlačenje lopte), što može imati drugačiji rezultat- ishod. Treba napomenuti da se rezultat može posmatrati na različite načine. "Izvukli smo loptu" je takođe rezultat. "Izvukli smo plavu loptu" rezultat je. "Izvukli smo ovu konkretnu loptu od svih mogućih lopti" - ovaj najmanje generalizovan pogled na rezultat naziva se elementarni ishod. U formuli za izračunavanje vjerovatnoće podrazumijevaju se elementarni ishodi.
Rješenje. Sada izračunavamo vjerovatnoću odabira plave lopte.
Događaj A: "odabrana lopta je ispala plava"
Ukupan broj svih mogućih ishoda: 9+3=12 (broj svih loptica koje smo mogli izvući)
Broj ishoda povoljnih za događaj A: 3 (broj takvih ishoda u kojima se dogodio događaj A - odnosno broj plavih loptica)
P(A)=3/12=1/4=0,25
Odgovor: 0,25
Izračunajmo za isti problem vjerovatnoću izbora crvene lopte.
Ukupan broj mogućih ishoda će ostati isti, 12. Broj povoljnih ishoda: 9. Željena vjerovatnoća: 9/12=3/4=0,75
Vjerovatnoća bilo kojeg događaja uvijek je između 0 i 1.
Ponekad se u svakodnevnom govoru (ali ne u teoriji vjerovatnoće!) vjerovatnoća događaja procjenjuje kao postotak. Prijelaz između matematičke i konverzacijske procjene se vrši množenjem (ili dijeljenjem) sa 100%.
dakle,
U ovom slučaju, vjerovatnoća je nula za događaje koji se ne mogu dogoditi - malo vjerovatno. Na primjer, u našem primjeru, to bi bila vjerovatnoća izvlačenja zelene lopte iz koša. (Broj povoljnih ishoda je 0, P(A)=0/12=0 ako se računa po formuli)
Vjerovatnoća 1 ima događaje koji će se apsolutno sigurno dogoditi, bez opcija. Na primjer, vjerovatnoća da će "odabrana lopta biti ili crvena ili plava" je za naš problem. (Broj povoljnih ishoda: 12, P(A)=12/12=1)
Pogledali smo klasičan primjer koji ilustruje definiciju vjerovatnoće. Svi slični USE zadatke prema teoriji vjerovatnoće rješavaju se primjenom ove formule.
Umjesto crvenih i plavih loptica mogu biti jabuke i kruške, dječaci i djevojčice, naučene i nenaučene tikete, karte koje sadrže i ne sadrže pitanje na temu (prototipovi, ), neispravne i kvalitetne torbe ili vrtne pumpe (prototipovi, ) - princip ostaje isti.
Malo se razlikuju u formulaciji problema teorije USE vjerovatnoće, gdje trebate izračunati vjerovatnoću da će se događaj dogoditi na određeni dan. ( , ) Kao iu prethodnim zadacima, potrebno je odrediti što je elementarni ishod, a zatim primijeniti istu formulu.
Primjer 2 Konferencija traje tri dana. Prvog i drugog dana po 15 govornika, trećeg dana 20. Kolika je vjerovatnoća da će izvještaj profesora M. pasti trećeg dana, ako se redoslijed izvještaja određuje žrijebom?
Šta je ovde osnovni ishod? - Dodjeljivanje profesorskog izvještaja jednom od svih mogućih serijski brojevi za nastup. U izvlačenju učestvuje 15+15+20=50 ljudi. Dakle, izvještaj profesora M. može dobiti jedan od 50 brojeva. To znači da postoji samo 50 elementarnih ishoda.
Koji su povoljni ishodi? - One u kojima se ispostavi da će profesor govoriti treći dan. Odnosno, zadnjih 20 brojeva.
Prema formuli, vjerovatnoća P(A)= 20/50=2/5=4/10=0,4
Odgovor: 0.4
Izvlačenje žrijeba je uspostavljanje slučajne korespondencije između ljudi i naručenih mjesta. U primjeru 2, uparivanje je razmatrano u smislu toga koja od mjesta određena osoba može zauzeti. Istoj situaciji možete pristupiti i s druge strane: koji bi od ljudi s kojom vjerovatnoćom mogao doći do određenog mjesta (prototipovi , , , ):
Primjer 3 U žrijebu učestvuje 5 Nijemaca, 8 Francuza i 3 Estonca. Kolika je vjerovatnoća da prvi (/drugi/sedmi/poslednji - nije bitno) bude Francuz.
Broj elementarnih ishoda je broj svih mogući ljudi ko bi mogao da stigne do ovog mesta žrebom. 5+8+3=16 osoba.
Povoljni ishodi - Francuzi. 8 osoba.
Željena vjerovatnoća: 8/16=1/2=0,5
Odgovor: 0,5
Prototip je malo drugačiji. Postoje zadaci o novčićima () i kockicama () koji su nešto kreativniji. Rješenja za ove probleme mogu se naći na stranicama prototipa.
Evo nekoliko primjera bacanja novčića ili kocke.
Primjer 4 Kada bacimo novčić, kolika je vjerovatnoća da ćemo dobiti repove?
Ishod 2 - glava ili rep. (veruje se da novčić nikada ne pada na ivicu) Povoljan ishod - repovi, 1.
Vjerovatnoća 1/2=0,5
Odgovor: 0,5.
Primjer 5Šta ako dvaput bacimo novčić? Kolika je vjerovatnoća da će se oba puta pojaviti?
Glavna stvar je odrediti koje ćemo elementarne ishode uzeti u obzir prilikom bacanja dva novčića. Nakon bacanja dva novčića, može se dogoditi jedan od sljedećih rezultata:
1) PP - oba puta je došlo do repova
2) PO - prvi put repovi, drugi put glave
3) OP - prvi put glava, drugi put rep
4) OO - glava gore oba puta
Nema drugih opcija. To znači da postoje 4 elementarna ishoda, samo je prvi povoljan, 1.
Vjerovatnoća: 1/4=0,25
Odgovor: 0,25
Kolika je vjerovatnoća da će dva bacanja novčića pasti na rep?
Broj elementarnih ishoda je isti, 4. Povoljni ishodi su drugi i treći, 2.
Verovatnoća dobijanja jednog repa: 2/4=0,5
U takvim problemima može dobro doći još jedna formula.
Ako pri jednom bacanju novčića imamo 2 moguća ishoda, tada će za dva bacanja rezultata biti 2 2=2 2 =4 (kao u primjeru 5), za tri bacanja 2 2 2=2 3 =8, za četiri : 2·2·2·2=2 4 =16, … za N bacanja mogućih ishoda bit će 2·2·...·2=2 N .
Dakle, možete pronaći vjerovatnoću da dobijete 5 repova od 5 bacanja novčića.
Ukupan broj elementarnih ishoda: 2 5 =32.
Povoljni ishodi: 1. (RRRRRR - svih 5 puta rep)
Verovatnoća: 1/32=0,03125
Isto važi i za kockice. Sa jednim bacanjem ima 6 mogućih rezultata.Dakle, za dva bacanja: 6 6=36, za tri 6 6 6=216 itd.
Primjer 6 Bacamo kocku. Kolika je vjerovatnoća da dobijete paran broj?
Ukupni ishodi: 6, prema broju lica.
Povoljno: 3 ishoda. (2, 4, 6)
Vjerovatnoća: 3/6=0,5
Primjer 7 Baci dve kocke. Kolika je vjerovatnoća da se ukupno baca 10? (zaokružiti na stotinke)
Postoji 6 mogućih ishoda za jednu kocku. Dakle, za dva, prema gornjem pravilu, 6·6=36.
Koji će ishodi biti povoljni da ukupno 10 ispadne?
10 se mora razložiti u zbir dva broja od 1 do 6. To se može učiniti na dva načina: 10=6+4 i 10=5+5. Dakle, za kocke su moguće opcije:
(6 na prvom i 4 na drugom)
(4 na prvom i 6 na drugom)
(5 na prvom i 5 na drugom)
Ukupno 3 opcije. Željena vjerovatnoća: 3/36=1/12=0,08
Odgovor: 0.08
Ostale vrste B6 problema će se raspravljati u jednom od sljedećih članaka "Kako riješiti".
slučajni događaj Svaki događaj koji se može ili ne mora dogoditi kao rezultat nekog iskustva.
Vjerovatnoća događaja R jednak je omjeru broja povoljnih ishoda k među svim mogućim ishodima. n, tj.
p=\frac(k)(n)
Formule za sabiranje i množenje teorije vjerovatnoće
\bar(A) događaj pozvao suprotno od događaja A, ako se događaj A nije dogodio.
Zbir vjerovatnoća suprotni događaji jednak je jedan, tj.
P(\bar(A)) + P(A) =1
- Vjerovatnoća događaja ne može biti veća od 1.
- Ako je vjerovatnoća događaja 0, onda se neće dogoditi.
- Ako je vjerovatnoća događaja 1, onda će se dogoditi.
Teorema o dodavanju vjerovatnoće:
"Vjerovatnoća zbira dva nekompatibilna događaja jednaka je zbiru vjerovatnoća ovih događaja."
P(A+B) = P(A) + P(B)
Vjerovatnoća iznosi dva zajednička događaja jednak je zbiru vjerovatnoća ovih događaja bez uzimanja u obzir njihove zajedničke pojave:
P(A+B) = P(A) + P(B) - P(AB)
Teorema množenja vjerovatnoće
„Vjerovatnoća proizvoda dva događaja jednaka je proizvodu vjerovatnoće jednog od njih po uslovna verovatnoća drugo, računato pod uslovom da se prvi dogodio.
P(AB)=P(A)*P(B)
Razvoj pozvao nekompatibilno, ako pojava jednog od njih isključuje pojavu drugih. Odnosno, može se dogoditi samo jedan određeni događaj, ili drugi.
Razvoj pozvao joint, osim ako pojava jednog od njih isključuje pojavu drugog.
Dva slučajna događaja A i B se zovu nezavisni, ako pojava jednog od njih ne mijenja vjerovatnoću pojave drugog. Inače, događaji A i B se nazivaju zavisni.