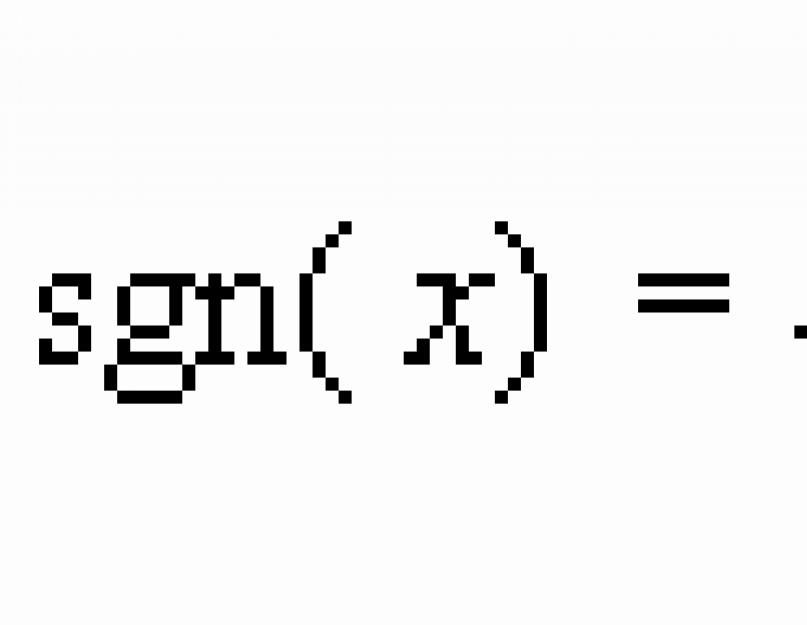Dažnai sprendžiant logaritmines nelygybes iškyla kintamos logaritmo bazės problemos. Taigi, formos nelygybė

yra standartinė mokyklos nelygybė. Paprastai jai išspręsti naudojamas perėjimas prie lygiaverčio sistemų rinkinio:

Šio metodo trūkumas yra būtinybė išspręsti septynias nelygybes, neskaičiuojant dviejų sistemų ir vienos aibės. Net ir esant nurodytoms kvadratinėms funkcijoms, populiacijos sprendimas gali užtrukti daug laiko.

Galima pasiūlyti alternatyvų, mažiau laiko reikalaujantį šios standartinės nelygybės sprendimo būdą. Norėdami tai padaryti, atsižvelgiame į šią teoremą.

Teorema 1. Tegu aibėje X nuolat didėjanti funkcija. Tada šioje aibėje funkcijos prieaugio ženklas sutaps su argumento prieaugio ženklu, t.y. , kur .

Pastaba: jei rinkinyje X nuolat mažėja funkcija, tada .

Grįžkime prie nelygybės. Pereikime prie dešimtainio logaritmo (galite pereiti prie bet kurio, kurio pastovi bazė yra didesnė už vieną).

Dabar galime naudoti teoremą, skaitiklyje pastebėdami funkcijų prieaugį ir vardiklyje. Taigi tai tiesa

Dėl to skaičiavimų, vedančių į atsakymą, skaičius sumažėja maždaug perpus, o tai sutaupo ne tik laiko, bet ir leidžia potencialiai padaryti mažiau aritmetinių ir neatsargių klaidų.

1 pavyzdys

Palyginus su (1) randame , , .

Pereidami į (2) turėsime:

2 pavyzdys

Lyginant su (1) randame , , .

Pereidami į (2) turėsime:

3 pavyzdys

Kadangi kairioji nelygybės pusė yra didėjanti funkcija ir , tada atsakymas nustatomas.

Pavyzdžių, kuriuose galima pritaikyti „Terme 1“, rinkinį galima nesunkiai išplėsti, jei atsižvelgsime į „Terme 2“.

Leisk į filmavimo aikštelę X funkcijos , , , yra apibrėžtos, o šioje aibėje ženklai ir sutampa, t.y. tada bus sąžininga.

4 pavyzdys

5 pavyzdys

Taikant standartinį metodą, pavyzdys sprendžiamas pagal schemą: sandauga yra mažesnė už nulį, kai faktoriai yra skirtingų ženklų. Tie. nagrinėjame dviejų nelygybių sistemų aibę, kurioje, kaip buvo nurodyta pradžioje, kiekviena nelygybė suskaidoma į dar septynias.

Jei atsižvelgsime į 2 teoremą, kiekvienas veiksnys, atsižvelgiant į (2), gali būti pakeistas kita funkcija, kuri turi tą patį ženklą šiame O.D.Z. pavyzdyje.

Funkcijos prieaugio pakeitimo argumento padidėjimu metodas, atsižvelgiant į 2 teoremą, pasirodo labai patogus sprendžiant tipines C3 USE problemas.

6 pavyzdys

7 pavyzdys

. Pažymėkime. Gauk

. Atminkite, kad pakeitimas reiškia: . Grįžę prie lygties, gauname .

8 pavyzdys

Mūsų naudojamose teoremose nėra jokių apribojimų funkcijų klasėms. Šiame straipsnyje, kaip pavyzdys, teoremos buvo pritaikytos logaritminių nelygybių sprendimui. Keli toliau pateikti pavyzdžiai parodys kitų tipų nelygybių sprendimo metodo žadą.

Ar manote, kad iki egzamino dar liko laiko ir turėsite laiko pasiruošti? Galbūt taip ir yra. Bet kokiu atveju, kuo anksčiau studentas pradeda treniruotis, tuo sėkmingiau jis išlaiko egzaminus. Šiandien nusprendėme skirti straipsnį logaritminėms nelygybėms. Tai viena iš užduočių, reiškianti galimybę gauti papildomą balą.

Ar jau žinai, kas yra logaritmas (logas)? Labai tikimės. Bet net jei neturite atsakymo į šį klausimą, tai nėra problema. Labai lengva suprasti, kas yra logaritmas.

Kodėl būtent 4? Turite padidinti skaičių 3 iki tokios galios, kad gautumėte 81. Kai suprasite principą, galite pereiti prie sudėtingesnių skaičiavimų.

Prieš kelerius metus išgyvenote nelygybę. Ir nuo to laiko juos nuolat sutinki matematikoje. Jei kyla problemų sprendžiant nelygybes, peržiūrėkite atitinkamą skyrių.
Dabar, kai susipažinsime su sąvokomis atskirai, pereisime prie jų svarstymo apskritai.

Paprasčiausia logaritminė nelygybė.

Paprasčiausios logaritminės nelygybės šiuo pavyzdžiu neapsiriboja, yra dar trys, tik su skirtingais ženklais. Kam to reikia? Norėdami geriau suprasti, kaip išspręsti nelygybę logaritmais. Dabar pateikiame labiau pritaikomą pavyzdį, vis dar gana paprastą, sudėtingas logaritmines nelygybes paliekame vėlesniam laikui.

Kaip tai išspręsti? Viskas prasideda nuo ODZ. Turėtumėte apie tai žinoti daugiau, jei norite visada lengvai išspręsti bet kokią nelygybę.

Kas yra ODZ? DPV logaritminėms nelygybėms

Santrumpa reiškia plotą leistinos vertės. Egzamino užduotyse ši formuluotė dažnai pasirodo. DPV jums naudingas ne tik logaritminių nelygybių atveju.

Dar kartą pažiūrėkite į aukščiau pateiktą pavyzdį. Remdamiesi juo svarstysime ODZ, kad suprastumėte principą, o logaritminių nelygybių sprendimas nekeltų klausimų. Iš logaritmo apibrėžimo matyti, kad 2x+4 turi būti didesnis už nulį. Mūsų atveju tai reiškia štai ką.

Šis skaičius pagal apibrėžimą turi būti teigiamas. Išspręskite aukščiau pateiktą nelygybę. Tai galima padaryti net žodžiu, čia aišku, kad X negali būti mažesnis už 2. Nelygybės sprendimas bus priimtinų reikšmių diapazono apibrėžimas.
Dabar pereikime prie paprasčiausios logaritminės nelygybės sprendimo.

Iš abiejų nelygybės dalių atmetame pačius logaritmus. Kas mums dėl to belieka? paprasta nelygybė.

Tai lengva išspręsti. X turi būti didesnis nei -0,5. Dabar mes sujungiame dvi gautas reikšmes į sistemą. Šiuo būdu,

Tai bus nagrinėjamos logaritminės nelygybės leistinų verčių sritis.

Kam išvis reikalingas ODZ? Tai galimybė atsikratyti neteisingų ir neįmanomų atsakymų. Jei atsakymas nepatenka į priimtinų verčių diapazoną, atsakymas tiesiog neturi prasmės. Tai verta prisiminti ilgą laiką, nes egzamine dažnai reikia ieškoti ODZ ir tai susiję ne tik su logaritminėmis nelygybėmis.

Logaritminės nelygybės sprendimo algoritmas

Sprendimas susideda iš kelių žingsnių. Pirma, būtina rasti priimtinų verčių diapazoną. ODZ bus dvi reikšmės, mes tai apsvarstėme aukščiau. Kitas žingsnis – išspręsti pačią nelygybę. Sprendimo metodai yra tokie:

• daugiklio pakeitimo metodas;
• skilimas;
• racionalizavimo metodas.

Priklausomai nuo situacijos, reikia naudoti vieną iš aukščiau pateiktų metodų. Eikime tiesiai prie sprendimo. Atskleisime populiariausią būdą, kuris tinka USE užduotims spręsti beveik visais atvejais. Toliau apsvarstysime skaidymo metodą. Tai gali padėti, jei susidursite su ypač „keblia“ nelygybe. Taigi, logaritminės nelygybės sprendimo algoritmas.

Sprendimo pavyzdžiai :

Ne veltui mes paėmėme būtent tokią nelygybę! Atkreipkite dėmesį į pagrindą. Atsiminkite: jei jis didesnis už vienetą, randant galiojančių reikšmių diapazoną, ženklas išlieka toks pat; kitu atveju reikia pakeisti nelygybės ženklą.

Dėl to gauname nelygybę:

Dabar pristatome kairė pusėį lygties formą, lygią nuliui. Vietoj ženklo „mažiau nei“ dedame „lygus“, išsprendžiame lygtį. Taigi, mes rasime ODZ. Tikimės, kad su tokiu sprendimu paprasta lygtis neturėsi problemų. Atsakymai yra -4 ir -2. Tai dar ne viskas. Turite parodyti šiuos taškus diagramoje, įdėti "+" ir "-". Ką reikia padaryti dėl to? Pakeiskite skaičius iš intervalų į išraišką. Kai reikšmės yra teigiamos, ten įdedame „+“.

Atsakymas: x negali būti didesnis nei -4 ir mažesnis nei -2.

Mes radome galiojančių verčių diapazoną tik kairėje pusėje, dabar turime rasti galiojančių verčių diapazoną dešinėje pusėje. Tai jokiu būdu nėra lengviau. Atsakymas: -2. Mes susikertame abi gautas sritis.

Ir tik dabar pradedame spręsti pačią nelygybę.

Kiek įmanoma supaprastinkime, kad būtų lengviau apsispręsti.

Sprendime vėl naudojame intervalo metodą. Praleiskime skaičiavimus, su juo viskas jau aišku iš ankstesnio pavyzdžio. Atsakymas.

Bet šis metodas tinka, jei logaritminė nelygybė turi tuos pačius pagrindus.

Sprendžiant logaritmines lygtis ir nelygybes su skirtingais pagrindais, pradinis redukavimas į vieną bazę. Tada naudokite aukščiau pateiktą metodą. Bet yra ir daugiau sunkus atvejis. Apsvarstykite vieną iš labiausiai sudėtingi tipai logaritmines nelygybes.

Logaritminės nelygybės su kintamu pagrindu

Kaip išspręsti tokias charakteristikas turinčias nelygybes? Taip, ir tokių galima rasti egzamine. Nelygybių sprendimas tokiu būdu taip pat turės teigiamos įtakos jūsų ugdymo procesas. Pažvelkime į problemą išsamiai. Padėkime teoriją į šalį ir eikime tiesiai į praktiką. Norint išspręsti logaritmines nelygybes, pakanka vieną kartą susipažinti su pavyzdžiu.

Norint išspręsti pateiktos formos logaritminę nelygybę, reikia sumažinti dešinę pusę iki logaritmo su ta pačia baze. Principas primena lygiaverčius perėjimus. Dėl to nelygybė atrodys taip.

Tiesą sakant, belieka sukurti nelygybių sistemą be logaritmų. Naudodami racionalizacijos metodą pereiname prie ekvivalentinės nelygybių sistemos. Pačią taisyklę suprasite, kai pakeisite atitinkamas reikšmes ir stebėsite jų pokyčius. Sistema turės tokias nelygybes.

Naudodami racionalizacijos metodą spręsdami nelygybes, turite atsiminti: iš pagrindo reikia atimti vieną, x pagal logaritmo apibrėžimą atimamas iš abiejų nelygybės dalių (dešinė iš kairės), du išraiškos padauginamos ir nustatomos pagal pradinį ženklą lyginant su nuliu.

Tolesnis sprendimas atliekamas intervalo metodu, čia viskas paprasta. Jums svarbu suprasti sprendimo būdų skirtumus, tada viskas pradės lengvai klotis.

AT logaritmines nelygybes daug niuansų. Paprasčiausius iš jų pakankamai lengva išspręsti. Kaip padaryti, kad kiekvienas iš jų būtų išspręstas be problemų? Šiame straipsnyje jau gavote visus atsakymus. Dabar jūsų laukia ilga praktika. Nuolat treniruokitės spręsdami įvairias problemas egzamino metu ir galėsite gauti aukščiausią balą. Sėkmės sunkiame darbe!

Logaritminės nelygybės

Ankstesnėse pamokose susipažinome su logaritminėmis lygtimis ir dabar žinome, kas jos yra ir kaip jas išspręsti. O šios dienos pamoka bus skirta logaritminių nelygybių tyrimui. Kas yra šios nelygybės ir kuo skiriasi logaritminės lygties sprendimas nuo nelygybių?

Logaritminės nelygybės yra nelygybės, kurios turi kintamąjį po logaritmo ženklu arba jo pagrindu.

Arba taip pat galima sakyti, kad logaritminė nelygybė yra nelygybė, kurioje jos nežinoma reikšmė, kaip ir logaritminėje lygtyje, bus po logaritmo ženklu.

Paprasčiausios logaritminės nelygybės atrodo taip:

kur f(x) ir g(x) yra kai kurios išraiškos, kurios priklauso nuo x.

Pažvelkime į tai naudodami tokį pavyzdį: f(x)=1+2x+x2, g(x)=3x−1.

Logaritminių nelygybių sprendimas

Prieš sprendžiant logaritmines nelygybes, verta atkreipti dėmesį į tai, kad jas išsprendus jos yra panašios į eksponentinės nelygybės, būtent:

Pirma, pereinant nuo logaritmų prie išraiškų po logaritmo ženklu, taip pat reikia palyginti logaritmo bazę su vienu;

Antra, sprendžiant logaritminę nelygybę naudojant kintamųjų pokytį, turime spręsti nelygybes pokyčio atžvilgiu, kol gausime paprasčiausią nelygybę.

Bet būtent mes svarstėme panašius logaritminių nelygybių sprendimo momentus. Dabar pažvelkime į gana reikšmingą skirtumą. Jūs ir aš žinome, kad logaritminė funkcija turi ribotą apibrėžimo sritį, todėl pereinant nuo logaritmų prie išraiškų, kurios yra po logaritmo ženklu, turite atsižvelgti į priimtinų reikšmių diapazoną (ODV).

Tai yra, reikia turėti omenyje, kad spręsdami logaritminę lygtį pirmiausia galime rasti lygties šaknis, o tada patikrinti šį sprendimą. Tačiau logaritminės nelygybės sprendimas tokiu būdu neveiks, nes pereinant nuo logaritmų prie išraiškų po logaritmo ženklu, reikės užrašyti nelygybės ODZ.

Be to, verta prisiminti, kad nelygybių teorija susideda iš realiųjų skaičių, kurie yra teigiami ir neigiami skaičiai, taip pat skaičius 0.

Pavyzdžiui, kai skaičius „a“ yra teigiamas, turi būti naudojamas toks užrašas: a > 0. Tokiu atveju ir šių skaičių suma ir sandauga taip pat bus teigiami.

Pagrindinis nelygybės sprendimo principas yra pakeisti ją paprastesne nelygybe, tačiau svarbiausia, kad ji būtų lygiavertė duotajai. Be to, mes taip pat gavome nelygybę ir vėl ją pakeitėme paprastesne forma ir pan.

Sprendžiant nelygybes su kintamuoju, reikia rasti visus jo sprendimus. Jei dvi nelygybės turi tą patį kintamąjį x, tai tokios nelygybės yra lygiavertės, jei jų sprendiniai yra vienodi.

Atliekant logaritminių nelygybių sprendimo užduotis, reikia atsiminti, kad kai a > 1, tada logaritminė funkcija didėja, o kai 0< a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить.

Logaritminių nelygybių sprendimo būdai

Dabar pažvelkime į kai kuriuos metodus, taikomus sprendžiant logaritmines nelygybes. Norėdami geriau suprasti ir įsisavinti, pabandysime juos suprasti naudodami konkrečius pavyzdžius.

Žinome, kad paprasčiausia logaritminė nelygybė turi tokią formą:

Šioje nelygybėje V - yra vienas iš tokių nelygybės ženklų kaip:<,>, ≤ arba ≥.

Kai šio logaritmo bazė yra didesnė už vieną (a>1), pereinant nuo logaritmų prie išraiškų po logaritmo ženklu, tada šioje versijoje nelygybės ženklas išsaugomas, o nelygybė atrodys taip:

kuri yra lygiavertė šiai sistemai:

Jei logaritmo bazė yra didesnė už nulį ir mažiau nei vienas (0

Tai atitinka šią sistemą:

Pažvelkime į daugiau paprasčiausių logaritminių nelygybių sprendimo pavyzdžių, parodytų paveikslėlyje žemiau:

Pavyzdžių sprendimas

Pratimas. Pabandykime išspręsti šią nelygybę:

Priimtinų verčių srities sprendimas.

Dabar pabandykime padauginti jo dešinę pusę iš:

Pažiūrėkime, ką galime padaryti:

Dabar pereikime prie sublogaritminių išraiškų transformacijos. Kadangi logaritmo pagrindas yra 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный:

3x - 8 > 16;
3x > 24;
x > 8.

Iš to išplaukia, kad gautas intervalas visiškai priklauso ODZ ir yra tokios nelygybės sprendimas.

Štai atsakymą gavome:

Ko reikia logaritminėms nelygybėms išspręsti?

Dabar pabandykime išanalizuoti, ko mums reikia norint sėkmingai išspręsti logaritmines nelygybes?

Pirmiausia sutelkite visą savo dėmesį ir stenkitės nesuklysti atlikdami transformacijas, kurios pateikiamos šioje nelygybėje. Taip pat reikia atsiminti, kad sprendžiant tokias nelygybes, būtina užkirsti kelią ODZ nelygybės išsiplėtimui ir susiaurėjimui, dėl kurio gali būti prarasti ar įgyti pašaliniai sprendimai.

Antra, sprendžiant logaritmines nelygybes, turite išmokti logiškai mąstyti ir suprasti skirtumą tarp tokių sąvokų kaip nelygybių sistema ir nelygybių rinkinys, kad galėtumėte lengvai pasirinkti nelygybės sprendimus, vadovaudamiesi jos DHS.

Trečia, norėdami sėkmingai išspręsti tokias nelygybes, kiekvienas iš jūsų turite puikiai žinoti visas elementariųjų funkcijų savybes ir aiškiai suprasti jų reikšmę. Tokios funkcijos apima ne tik logaritmines, bet ir racionaliąsias, galios, trigonometrines ir pan., žodžiu, visas tas, kurias studijavote. mokslus algebra.

Kaip matote, išstudijavus logaritminių nelygybių temą, nėra nieko sudėtingo sprendžiant šias nelygybes, jei esate dėmesingas ir atkaklus siekdamas savo tikslų. Kad nekiltų problemų sprendžiant nelygybes, reikia kuo daugiau treniruotis, sprendžiant įvairias užduotis ir tuo pačiu įsiminti pagrindinius tokių nelygybių sprendimo būdus ir jų sistemas. Nesėkmingai sprendę logaritmines nelygybes, turėtumėte atidžiai išanalizuoti savo klaidas, kad ateityje prie jų nebegrįžtumėte.

Namų darbai

Norėdami geriau įsisavinti temą ir konsoliduoti nagrinėjamą medžiagą, išspręskite šias nelygybes:

Nelygybė vadinama logaritmine, jei joje yra logaritminė funkcija.

Logaritminių nelygybių sprendimo metodai niekuo nesiskiria, išskyrus du dalykus.

Pirma, pereinant nuo logaritminės nelygybės prie sublogaritminių funkcijų nelygybės, išplaukia vadovaukitės gautos nelygybės ženklu. Jis laikosi šios taisyklės.

Jei logaritminės funkcijos bazė didesnė už $1$, tai pereinant nuo logaritminės nelygybės prie poblogaritminių funkcijų nelygybės, nelygybės ženklas išsaugomas, o jei mažesnis už $1$, tada apverčiamas.

Antra, bet kurios nelygybės sprendimas yra intervalas, todėl poblogaritminių funkcijų nelygybės sprendinio pabaigoje reikia sudaryti dviejų nelygybių sistemą: pirmoji šios sistemos nelygybė bus sublogaritmines funkcijas, o antrasis bus į logaritminę nelygybę įtrauktų logaritminių funkcijų apibrėžimo srities intervalas.

Praktika.

Išspręskime nelygybes:

1. $\log_(2)((x+3)) \geq 3.$

$D(y): \x+3>0.$

$x \in (-3;+\infty)$

Logaritmo pagrindas yra $2>1$, todėl ženklas nesikeičia. Naudodami logaritmo apibrėžimą, gauname:

$x+3 \geq 2^(3),$

$x \in )