Įvykio $A$ tikimybė yra $A$ palankių baigčių skaičiaus ir visų vienodai galimų baigčių skaičiaus santykis
$P(A)=(m)/(n)$, kur $n$ yra bendras galimų rezultatų skaičius, o $m$ – $A$ palankių rezultatų skaičius.
Įvykio tikimybė yra skaičius iš segmento $$
Taksi įmonė turi 50 USD automobilių. $35 $ iš jų yra juodos spalvos, likusi dalis yra geltona. Raskite tikimybę, kad geltonas automobilis atvyks atsitiktinai.
Raskite geltonų automobilių skaičių:
Iš viso yra 50 USD automobilių, tai yra, vienas iš penkiasdešimties atvyks į skambutį. Yra 15 USD geltonų automobilių, todėl tikimybė, kad atvažiuos geltona mašina, yra $(15)/(50)=(3)/(10)=0,3$
Atsakymas: 0,3 USD
Priešingi įvykiai
Sakoma, kad du įvykiai yra priešingi, jei tam tikrame bandyme jie yra nesuderinami ir vienas iš jų būtinai įvyksta. Priešingų įvykių tikimybės sudaro 1. Įvykis, priešingas įvykiui $A$, rašomas $((A))↖(-)$.
$P(A)+P((A))↖(-)=1$
Nepriklausomi renginiai
Sakoma, kad du įvykiai $A$ ir $B$ yra nepriklausomi, jei kiekvieno iš jų atsiradimo tikimybė nepriklauso nuo to, ar įvyko kitas įvykis, ar ne. Kitu atveju įvykiai vadinami priklausomais.
Dviejų nepriklausomų įvykių $A$ ir $B$ sandaugos tikimybė yra lygi šių tikimybių sandaugai:
$P(A B)=P(A) P(B)$
Ivanas Ivanovičius nusipirko du skirtingus loterijos bilietus. Tikimybė, kad laimės pirmasis loterijos bilietas, yra lygus 0,15 USD. Tikimybė, kad laimės antrasis loterijos bilietas yra 0,12 USD. Ivanas Ivanovičius dalyvauja abiejuose burtuose. Darant prielaidą, kad lygiosios vyksta nepriklausomai vienas nuo kito, suraskite tikimybę, kad Ivanas Ivanovičius laimės abiejose lygiosiose.
Tikimybė $P(A)$ – laimi pirmą bilietą.
Tikimybė $P(B)$ – laimi antrą bilietą.
Renginiai $A$ ir $B$ yra nepriklausomi įvykiai. Tai yra, norėdami rasti tikimybę, kad įvyks abu įvykiai, turite rasti tikimybių sandaugą
$P(A B)=P(A) P(B)$
$P = 0,15 0,12 = 0,018 $
Atsakymas: 0,018 USD
Nesuderinami įvykiai
Teigiama, kad du įvykiai $A$ ir $B$ yra nesuderinami, jei nėra rezultatų, palankių ir įvykiams $A$, ir $B$. (Įvykiai, kurie negali vykti vienu metu)
Dviejų nesuderinamų įvykių $A$ ir $B$ sumos tikimybė yra lygi šių įvykių tikimybių sumai:
$P(A+B)=P(A)+P(B)$
Algebros egzamine studentas gauna vieną klausimą iš visų egzaminų. Tikimybė, kad tai yra klausimas tema " Kvadratinės lygtys“, yra lygus 0,3 USD. Tikimybė, kad tai yra klausimas tema " Iracionalios lygtys“, yra lygus 0,18 USD. Nėra klausimų, susijusių su šiomis dviem temomis vienu metu. Raskite tikimybę, kad studentas per egzaminą gaus klausimą viena iš šių dviejų temų.
Šie įvykiai vadinami nesuderinamais, nes studentas gaus klausimą ARBA tema „Kvadratinės lygtys“, ARBA tema „Iracionalios lygtys“. Temų negalima užfiksuoti vienu metu. Dviejų nesuderinamų įvykių $A$ ir $B$ sumos tikimybė yra lygi šių įvykių tikimybių sumai:
$P(A+B)=P(A)+P(B)$
P $ \u003d 0,3 + 0,18 \u003d 0,48 $
Atsakymas: 0,48 USD
Bendri renginiai
Du įvykiai laikomi bendrais, jei vieno iš jų įvykis neatmeta galimybės įvykti kito tame pačiame tyrime. Priešingu atveju įvykiai vadinami nesuderinamais.
Dviejų bendrų įvykių $A$ ir $B$ sumos tikimybė yra lygi šių įvykių tikimybių sumai, atėmus jų sandaugos tikimybę:
$P(A+B)=P(A)+P(B)-P(A B)$
Kino teatro vestibiulyje stovi du vienodi kavos aparatai. Tikimybė, kad kavos aparate baigsis iki dienos pabaigos, yra 0,6 USD. Tikimybė, kad abiejuose aparatuose pritrūks kavos, yra 0,32 USD. Raskite tikimybę, kad iki dienos pabaigos bent viename iš automatų pritrūks kavos.
Pažymime įvykius, tegul:
$A$ = kava baigsis pirmajame aparate,
$B$ = kava baigsis antrame aparate.
$A B =$ kava baigsis abiejuose automatuose,
$A + B =$ kava baigsis bent viename automate.
Pagal susitarimą $P(A) = P(B) = 0,6; P(A B) = 0,32 USD.
Įvykiai $A$ ir $B$ yra jungtiniai, dviejų bendrų įvykių sumos tikimybė yra lygi šių įvykių tikimybių sumai, sumažintai jų sandaugos tikimybe:
$P(A + B) = P(A) + P(B) − P(A B) = 0,6 + 0,6 - 0,32 = 0,88 $
Tikimybė. Matematikos profilinio egzamino užduotys.
Parengė matematikos mokytojas MBOU „Licėjus Nr. 4“, Ruzaevka
Ovčinikova T.V.

Tikimybės apibrėžimas
Tikimybė įvykiai Skambinkite skaičiaus santykis m šiam renginiui palankių rezultatų iš viso n visi vienodai galimi nesuderinami įvykiai, kurie gali atsirasti dėl vieno bandymo ar stebėjimo:
m
n
Leisti k - monetų išmetimų skaičius, tada galimų rezultatų skaičius: n=2 k .
Leisti k - kauliukų metimų skaičius, tada galimų rezultatų skaičius: n=6 k .

Atsitiktinio eksperimento metu simetriška moneta metama du kartus. Raskite tikimybę, kad galvutės pasirodys tiksliai vieną kartą.
Sprendimas.
Tik 4 variantai: apie; oi oi; p p; p p; apie .
2 palankus: apie; R ir R; apie .
Tikimybė yra 2/4 = 1/2 = 0,5 .
Atsakymas: 0,5.

Atsitiktinio eksperimento metu metami du kauliukai. Raskite tikimybę iš viso gauti 8 taškus. Rezultatą suapvalinkite iki artimiausio šimtosios dalies.
Sprendimas.
Kauliukai yra 6 pusių kauliukai. Pirmasis kauliukas gali mesti 1, 2, 3, 4, 5 arba 6 taškus. Kiekviena taškų parinktis atitinka 6 balų parinktis ant antrojo kauliuko.
Tie. Iš viso įvairių variantų 6x6=36.
Pasirinkimai (eksperimento rezultatai) bus tokie:
1; 1 1; 2 1; 3 1; 4 1; 5 1; 6
2; 1 2; 2 2; 3 2; 4 2; 5 2; 6
ir tt ...........................
6; 1 6; 2 6; 3 6; 4 6; 5 6; 6
Suskaičiuokime baigčių (parinkčių) skaičių, kai dviejų kauliukų taškų suma yra 8.
2; 6 3; 5; 4; 4 5; 3 6; 2.
Tik 5 variantai.
Raskime tikimybę: 5/36 = 0,138 ≈ 0,14.
Atsakymas: 0,14.

Biologijos bilietų kolekcijoje iš viso yra 55 bilietai, 11 iš jų yra botanikos klausimas. Raskite tikimybę, kad atsitiktinai pasirinktame egzamino biliete studentas gaus botanikos klausimą.
Sprendimas:
Tikimybė, kad atsitiktinai pasirinktame egzamino biliete studentas gaus botanikos klausimą yra 11/55 = 1/5 = 0,2.
Atsakymas: 0,2.

Gimnastikos čempionate dalyvauja 20 sportininkų: 8 iš Rusijos, 7 iš JAV, likusieji iš Kinijos. Gimnastų pasirodymo tvarka nustatoma burtų keliu. Raskite tikimybę, kad sportininkas, kuris rungtyniauja pirmasis, yra iš Kinijos.
Sprendimas.
Iš viso yra 20 sportininkų.
iš jų 20 – 8 – 7 = 5 sportininkai iš Kinijos.
Tikimybė, kad sportininkas, kuris varžysis pirmas, bus iš Kinijos, yra 5/20 = 1/4 = 0,25.
Atsakymas: 0,25.

Mokslinė konferencija vyksta po 5 dienų. Iš viso suplanuoti 75 pranešimai – pirmos trys dienos, po 17 pranešimų, likusieji po lygiai paskirstomi tarp ketvirtos ir penktos dienos. Ataskaitų tvarka nustatoma burtų keliu. Kokia tikimybė, kad profesoriaus M. pranešimas bus suplanuotas paskutinę konferencijos dieną?
Sprendimas:
Numatyta paskutinė konferencijos diena
(75 - 17 × 3) : 2 = 12 ataskaitų.
Tikimybė, kad profesoriaus M. pranešimas bus suplanuotas paskutinę konferencijos dieną, yra 12/75 = 4/25 = 0,16.
Atsakymas: 0,16.

Prieš prasidedant pirmajam badmintono čempionato ratui, dalyviai burtų keliu suskirstomi į žaidimų poras. Iš viso čempionate dalyvauja 26 badmintonininkai, tarp jų 10 dalyvių iš Rusijos, tarp jų ir Ruslanas Orlovas. Rasti tikimybę, kad pirmame rate Ruslanas Orlovas žais su bet kuriuo badmintonininku iš Rusijos?
Sprendimas:
Reikia pažymėti, kad Ruslanas Orlovas turi žaisti su kokiu nors badmintonininku iš Rusijos. O pats Ruslanas Orlovas taip pat yra iš Rusijos.
Tikimybė, kad pirmame rate Ruslanas Orlovas žais su bet kuriuo badmintonininku iš Rusijos, yra 9/25 = 36/100 = 0,36.
Atsakymas: 0,36.

Daša meta du kartus kauliukai. Iš viso ji surinko 8 taškus. Raskite tikimybę gauti 2 iš pirmo metimo.
Sprendimas.
Iš viso du kauliukai turėtų išmesti 8 taškus. Tai įmanoma, jei yra šie deriniai:
Tik 5 variantai. Suskaičiuokime baigčių (parinkčių) skaičių, kai iš pirmo metimo krito 2 taškai.
Ši parinktis yra 1.
Raskite tikimybę: 1/5 = 0,2.
Atsakymas: 0,2.

Pasaulio čempionate dalyvauja 20 komandų. Partijų pagalba jie turi būti suskirstyti į penkias grupes po keturias komandas. Dėžutėje yra mišrios kortelės su grupių numeriais:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5.
Komandos kapitonai ištraukia po vieną kortelę. Kokia tikimybė, kad Rusijos komanda bus trečioje grupėje.
Sprendimas:
Iš viso yra 20 komandų, 5 grupės.
Kiekvienoje grupėje yra 4 komandos.
Taigi iš viso gavome 20 baigčių, reikėjo 4, vadinasi, tikimybė, kad norimas rezultatas iškris, yra 4/20 = 0,2.
Atsakymas: 0,2.

Dvi gamyklos gamina tą patį stiklą automobilių žibintams. Pirmoje gamykloje šių stiklų pagaminama 45 proc., antroje – 55 proc. Pirmoji gamykla gamina 3% brokuotų stiklų, o antroji – 1%. Raskite tikimybę, kad netyčia parduotuvėje pirktas stiklas bus sugedęs.
Sprendimas:
Tikimybė, kad stiklas pirktas pirmoje gamykloje ir jis yra brokuotas:
R 1 = 0,45 0,03 = 0,0135.
Tikimybė, kad stiklas pirktas antroje gamykloje ir jis yra brokuotas:
R 2 = 0,55 0,01 = 0,0055.
Todėl pagal formulę visa tikimybe tikimybė, kad netyčia parduotuvėje pirktas stiklas bus brokuotas, lygi
p = p 1 + p 2 = 0,0135 + 0,0055 = 0,019.
Atsakymas: 0,019.

Jei didmeistris A. žaidžia baltaodžiai, tai jis laimi didmeistrą B. su 0,52 tikimybe. Jei A. žaidžia juodai, tai A. įveikia B. su 0,3 tikimybe.
Didmeistriai A. ir B. žaidžia du žaidimus, o antrajame pakeičia figūrų spalvą. Raskite tikimybę, kad A. laimės abu kartus.
Sprendimas:
Šansai laimėti pirmąjį ir antrąjį žaidimus nepriklauso vienas nuo kito. Nepriklausomų įvykių atsiradimo tikimybė yra lygi jų tikimybių sandaugai:
p = 0,52 0,3 = 0,156.
Atsakymas: 0,156.

Biatlonininkas į taikinius šaudo penkis kartus. Tikimybė vienu šūviu pataikyti į taikinį yra 0,8. Raskite tikimybę, kad biatlonininkas pirmus tris kartus pataikė į taikinius, o paskutinius du nepataikė. Rezultatą suapvalinkite iki artimiausio šimtosios dalies.
Sprendimas:
Kiekvieno kito šūvio rezultatas nepriklauso nuo ankstesnių. Todėl įvykiai „pataikė į pirmąjį šūvį“, „pataikė antruoju šūviu“ ir kt. nepriklausomas.
Kiekvieno pataikymo tikimybė yra 0,8. Taigi tikimybė praleisti yra 1 - 0,8 = 0,2.
1 šūvis: 0,8
2 smūgiai: 0,8
3 smūgiai: 0,8
4 smūgiai: 0,2
5 smūgiai: 0,2
Pagal nepriklausomų įvykių tikimybių dauginimo formulę nustatome, kad norima tikimybė yra lygi:
0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 = 0,02048 ≈ 0,02.
Atsakymas: 0,02.

Parduotuvėje yra du mokėjimo automatai. Kiekvienas iš jų gali būti sugedęs su 0,05 tikimybe, nepriklausomai nuo kito automato. Raskite tikimybę, kad bent vieną automatą galima naudoti.
Sprendimas:
Raskite tikimybę, kad abu automatai yra sugedę.
Šie įvykiai yra nepriklausomi, jų sandaugos tikimybė yra lygi šių įvykių tikimybių sandaugai:
0,05 0,05 = 0,0025.
Įvykis, kurį sudaro tai, kad bent vienas automatas yra tinkamas naudoti, yra priešingas.
Todėl jo tikimybė yra
1 − 0,0025 = 0,9975.
Atsakymas: 0,9975.

Kaubojus Džonas pataiko musę į sieną su 0,9 tikimybe, jei šaudo iš revolverio. Jei Jonas iššauna nešautą revolverį, jis pataiko į musę su 0,2 tikimybe. Ant stalo yra 10 revolverių, iš kurių tik 4 šaudomi. Kaubojus Džonas pamato musę ant sienos, atsitiktinai paima pirmą pasitaikiusį revolverį ir šauna į musę. Raskite tikimybę, kad Jonas praleis.
Sprendimas:
Tikimybė, kad Jonas nepamatys, jei paims revolverį, yra:
0,4 (1–0,9) = 0,04
Tikimybė, kad Jonas nepamatys, jei paims nepašautą revolverį, yra:
0,6 (1–0,2) = 0,48
Šie įvykiai yra nesuderinami, jų sumos tikimybė yra lygi šių įvykių tikimybių sumai:
0,04 + 0,48 = 0,52.
Atsakymas: 0,52.

Artilerijos šaudymo metu automatinė sistema atlieka šūvį į taikinį. Jei taikinys nesunaikinamas, sistema vėl šaudo. Šūviai kartojami tol, kol taikinys sunaikinamas. Tikimybė sunaikinti tam tikrą taikinį pirmu šūviu yra 0,4, o su kiekvienu tolesniu šūviu - 0,6. Kiek šūvių reikės norint užtikrinti, kad taikinio sunaikinimo tikimybė būtų bent 0,98?
Sprendimas:
Galite išspręsti problemą „veiksmais“, apskaičiuodami tikimybę išgyventi po nuoseklių praleidimų:
P(1) = 0,6;
P(2) = P(1) 0,4 = 0,24;
P(3) = P(2) 0,4 = 0,096;
P(4) = P(3) 0,4 = 0,0384;
P(5) = P(4) 0,4 = 0,01536.
Paskutinė tikimybė mažesnė nei 0,02, todėl pakanka penkių šūvių į taikinį.
Atsakymas: 5.

Klasėje yra 26 žmonės, tarp jų du dvyniai - Andrejus ir Sergejus. Klasė atsitiktinai suskirstyta į dvi grupes po 13 žmonių. Raskite tikimybę, kad Andrejus ir Sergejus bus toje pačioje grupėje.
Sprendimas:
Tegul vienas iš dvynių būna kokioje nors grupėje.
Kartu su juo grupėje bus 12 žmonių iš 25 likusių klasiokų.
Tikimybė, kad tarp šių 12 žmonių bus antrasis dvynys, lygi
P=12:25=0,48.
Atsakymas: 0,48.

Nuotraukoje pavaizduotas labirintas. Voras įšliaužia į labirintą taške „Įėjimas“. Voras negali apsisukti ir šliaužti atgal, todėl prie kiekvienos šakutės voras pasirenka vieną iš takų, kuriais dar nenušliaužė. Darant prielaidą, kad tolesnio kelio pasirinkimas yra visiškai atsitiktinis, nustatykite, su kokia tikimybe voras išeis iš D.
Sprendimas:
Kiekvienoje iš keturių pažymėtų šakių voras gali pasirinkti kelią, vedantį į išvažiavimą D, arba kitą kelią su 0,5 tikimybe. Tai nepriklausomi įvykiai, jų sandaugos tikimybė (voras pasiekia išėjimą D) lygi šių įvykių tikimybių sandaugai. Todėl tikimybė patekti į išvestį D yra (0,5) 4 = 0,0625.
Iki šiol pateikta atvirame matematikos USE problemų banke (mathege.ru), kurios sprendimas pagrįstas tik viena formule, kuri yra klasikinis tikimybės apibrėžimas.
Lengviausias būdas suprasti formulę yra pavyzdžiai.
1 pavyzdys Krepšelyje yra 9 raudoni ir 3 mėlyni kamuoliukai. Kamuoliukai skiriasi tik spalva. Atsitiktinai (nežiūrėdami) gauname vieną iš jų. Kokia tikimybė, kad tokiu būdu pasirinktas rutulys bus mėlynas?
komentuoti. Tikimybių teorijos uždaviniuose kažkas nutinka (į Ši byla mūsų veiksmas ištraukti kamuolį), kuris gali turėti kitoks rezultatas- rezultatas. Reikėtų pažymėti, kad rezultatas gali būti vertinamas įvairiais būdais. „Ištraukėme kamuolį“ – taip pat rezultatas. „Mes ištraukėme mėlyną kamuolį“ – toks rezultatas. „Iš visų įmanomų kamuoliukų ištraukėme būtent šį rutulį“ – toks mažiausiai apibendrintas rezultato vaizdas vadinamas elementariu rezultatu. Tikimybės apskaičiavimo formulėje reiškiami pagrindiniai rezultatai.
Sprendimas. Dabar apskaičiuojame tikimybę pasirinkti mėlyną rutulį.
Įvykis A: „pasirinktas rutulys pasirodė mėlynas“
Bendras visų galimų rezultatų skaičius: 9+3=12 (visų kamuoliukų, kuriuos galėtume ištraukti, skaičius)
A įvykiui palankių baigčių skaičius: 3 (tokių baigčių, kurių metu įvyko A įvykis, skaičius, tai yra mėlynų kamuoliukų skaičius)
P(A)=3/12=1/4=0,25
Atsakymas: 0,25
Apskaičiuokime tai pačiai problemai raudono rutulio pasirinkimo tikimybę.
Bendras galimų baigčių skaičius išliks toks pat – 12. Palankių baigčių skaičius: 9. Norima tikimybė: 9/12=3/4=0,75
Bet kurio įvykio tikimybė visada yra nuo 0 iki 1.
Kartais kasdieninėje kalboje (bet ne tikimybių teorijoje!) įvykių tikimybė įvertinama procentais. Perėjimas tarp matematinio ir pokalbio vertinimo atliekamas padauginus (arba padalijus) iš 100%.
Taigi,
Šiuo atveju įvykiams, kurie negali įvykti, tikimybė lygi nuliui – mažai tikėtina. Pavyzdžiui, mūsų pavyzdyje tai būtų tikimybė ištraukti žalią kamuolį iš krepšio. (palankių rezultatų skaičius yra 0, P(A)=0/12=0, jei skaičiuojama pagal formulę)
1 tikimybė turi įvykių, kurie tikrai įvyks be pasirinkimų. Pavyzdžiui, tikimybė, kad „pasirinktas rutulys bus raudonas arba mėlynas“, yra mūsų problema. (palankių rezultatų skaičius: 12, P(A) = 12/12 = 1)
Mes pažvelgėme į klasikinį pavyzdį, iliustruojantį tikimybės apibrėžimą. Visi panašūs NAUDOKITE užduotis pagal tikimybių teoriją išsprendžiami taikant šią formulę.
Vietoj raudonų ir mėlynų kamuoliukų gali būti obuolių ir kriaušių, berniukų ir mergaičių, išmoktų ir neišmoktų bilietų, bilietų, kuriuose yra ir nėra klausimo tam tikra tema (prototipai, ), brokuoti ir kokybiški krepšiai ar sodo siurbliai (prototipai). , ) – principas išlieka tas pats.
Šiek tiek skiriasi teorijos problemos formulavimas NAUDOTI tikimybes, kur reikia apskaičiuoti tikimybę, kad įvykis įvyks konkrečią dieną. ( , ) Kaip ir ankstesnėse užduotyse, turite nustatyti, kas yra elementarus rezultatas, ir tada taikyti tą pačią formulę.
2 pavyzdys Konferencija trunka tris dienas. Pirmą ir antrą dieną po 15 pranešėjų, trečią - 20. Kokia tikimybė, kad profesoriaus M. pranešimas iškris trečią dieną, jei pranešimų eilė bus nustatyta burtų keliu?
Koks čia elementarus rezultatas? - Profesoriaus pranešimo priskyrimas vienam iš visų galimų serijos numeriai už spektaklį. Burtuose dalyvauja 15+15+20=50 žmonių. Taigi, profesoriaus M. ataskaita gali gauti vieną iš 50 numerių. Tai reiškia, kad yra tik 50 pagrindinių rezultatų.
Kokie yra palankūs rezultatai? – Tos, kuriose paaiškėja, kad profesorius kalbės trečią dieną. Tai yra, paskutiniai 20 skaičių.
Pagal formulę tikimybė P(A)= 20/50=2/5=4/10=0,4
Atsakymas: 0,4
Burtų traukimas čia yra atsitiktinio susirašinėjimo tarp žmonių ir užsakytų vietų nustatymas. 2 pavyzdyje atitikimas buvo svarstomas atsižvelgiant į tai, kurią vietą konkretus asmuo gali užimti. Tą pačią situaciją galite pažvelgti iš kitos pusės: kuris iš žmonių su kokia tikimybe galėtų patekti į tam tikrą vietą (prototipai , , , ):
3 pavyzdys Burtuose dalyvauja 5 vokiečiai, 8 prancūzai ir 3 estai. Kokia tikimybė, kad pirmasis (/antras/septintas/paskutinis – nesvarbu) bus prancūzas.
Elementarių rezultatų skaičius yra visų skaičius galimi žmonės kurie galėtų patekti į šią vietą burtų keliu. 5+8+3=16 žmonių.
Palankūs rezultatai – prancūzai. 8 žmonės.
Norima tikimybė: 8/16=1/2=0,5
Atsakymas: 0,5
Prototipas šiek tiek skiriasi. Yra užduočių apie monetas () ir kauliukus (), kurios yra šiek tiek kūrybiškesnės. Šių problemų sprendimus galima rasti prototipų puslapiuose.
Štai keletas monetų arba kauliukų mėtymo pavyzdžių.
4 pavyzdys Kai mes metame monetą, kokia tikimybė gauti uodegą?
2 rezultatai – galvos arba uodegos. (manoma, kad moneta niekada nenukrenta ant krašto) Palankus rezultatas - uodegos, 1.
Tikimybė 1/2=0,5
Atsakymas: 0,5.
5 pavyzdys O kas, jei monetą išverstume du kartus? Kokia tikimybė, kad jis iškils į galvą abu kartus?
Svarbiausia yra nustatyti, į kokius elementarius rezultatus atsižvelgsime mesdami dvi monetas. Išmetus dvi monetas gali atsirasti vienas iš šių rezultatų:
1) PP – abu kartus jis iškilo
2) PO - pirmą kartą uodegos, antrą kartą galvos
3) OP - pirmą kartą galvos, antrą kartą - uodegos
4) OO – abu kartus galva aukštyn
Kitų variantų nėra. Tai reiškia, kad yra 4 elementarūs rezultatai. Tik pirmasis yra palankus, 1.
Tikimybė: 1/4=0,25
Atsakymas: 0,25
Kokia tikimybė, kad du monetos metimai nukris ant uodegos?
Elementarių baigčių skaičius yra toks pat, 4. Palankios baigtys yra antra ir trečia, 2.
Tikimybė gauti vieną uodegą: 2/4=0,5
Esant tokioms problemoms, gali praversti kita formulė.
Jei vienu monetos metimu turime 2 galimus rezultatus, tai dviejų metimų rezultatai bus 2 2=2 2 =4 (kaip 5 pavyzdyje), trimis metimais 2 2 2=2 3 =8, keturiems : 2·2·2·2=2 4 =16, … N galimų baigčių metimams bus 2·2·...·2=2 N .
Taigi, galite rasti tikimybę gauti 5 uodegas iš 5 monetų išmetimo.
Bendras elementarių rezultatų skaičius: 2 5 =32.
Palankūs rezultatai: 1. (RRRRRR – visi 5 kartus uodegos)
Tikimybė: 1/32=0,03125
Tas pats pasakytina ir apie kauliukus. Vienu metimu galimi rezultatai 6. Taigi dviem metimams: 6 6=36, trims 6 6 6=216 ir t.t.
6 pavyzdys Metame kauliuką. Kokia tikimybė gauti lyginį skaičių?
Iš viso rezultatų: 6, atsižvelgiant į veidų skaičių.
Palankus: 3 rezultatai. (2, 4, 6)
Tikimybė: 3/6=0,5
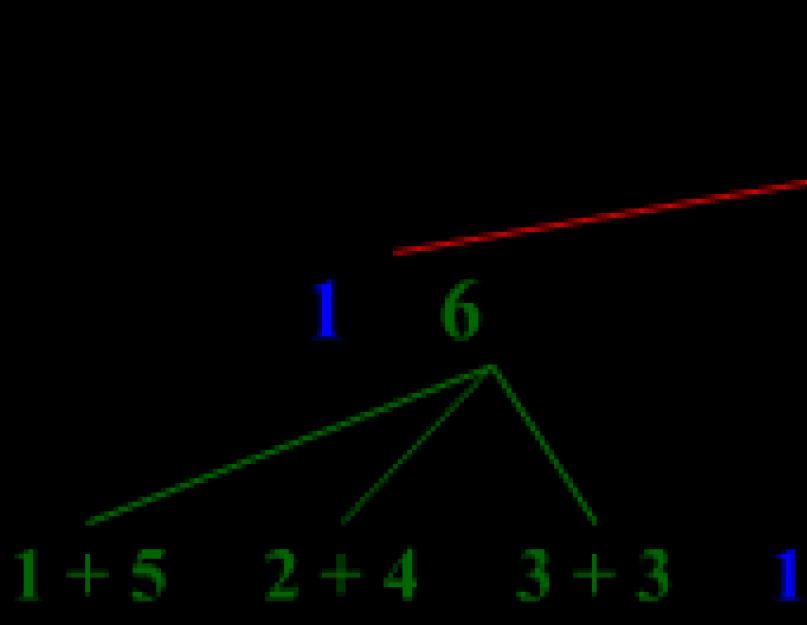
7 pavyzdys Mesti du kauliukus. Kokia tikimybė, kad bendra suma iškris 10? (apvalinti iki šimtųjų)
Yra 6 galimi vieno mirties padariniai. Vadinasi, dviems pagal aukščiau pateiktą taisyklę 6·6=36.
Kokie rezultatai bus palankūs, kad iš viso iškristų 10?
10 reikia išskaidyti į dviejų skaičių nuo 1 iki 6 sumą. Tai galima padaryti dviem būdais: 10=6+4 ir 10=5+5. Taigi, kubeliams galimi variantai:
(6 pirmoje ir 4 antroje)
(4 pirmoje ir 6 antroje)
(5 pirmoje ir 5 antroje)
Iš viso 3 variantai. Norima tikimybė: 3/36=1/12=0,08
Atsakymas: 0,08
Kiti B6 problemų tipai bus aptariami viename iš šių „Kaip išspręsti“ straipsnių.
atsitiktinis įvykis Bet koks įvykis, kuris gali įvykti arba neįvykti dėl tam tikros patirties.
Įvykio tikimybė R yra lygus palankių rezultatų skaičiaus santykiui k tarp visų galimų rezultatų. n, t.y.
p=\frac(k)(n)
Tikimybių teorijos sudėties ir daugybos formulės
\bar(A) įvykis paskambino priešingas įvykiui A, jei įvykis A neįvyko.
Tikimybių suma priešingi įvykiai lygūs vienetui, t.y.
P(\bar(A)) + P(A) =1
- Įvykio tikimybė negali būti didesnė nei 1.
- Jei įvykio tikimybė yra 0, tai neįvyks.
- Jei įvykio tikimybė yra 1, tai įvyks.
Tikimybių sudėjimo teorema:
"Dviejų nesuderinamų įvykių sumos tikimybė yra lygi šių įvykių tikimybių sumai."
P(A+B) = P(A) + P(B)
Tikimybė sumos du bendri renginiai yra lygi šių įvykių tikimybių sumai, neatsižvelgiant į jų bendrą atsiradimą:
P(A+B) = P(A) + P(B) – P(AB)
Tikimybių daugybos teorema
„Dviejų įvykių sandaugos tikimybė yra lygi vieno iš jų tikimybių sandaugai sąlyginė tikimybė kitas, skaičiuojamas su sąlyga, kad įvyko pirmasis.
P(AB)=P(A)*P(B)
Vystymai paskambino nesuderinamas, jei vieno iš jų išvaizda pašalina kitų išvaizdą. Tai yra, gali įvykti tik vienas konkretus įvykis arba kitas.
Vystymai paskambino Bendras, nebent vieno iš jų atsiradimas užkerta kelią kito atsiradimui.
Du atsitiktiniai įvykiai A ir B vadinami nepriklausomas, jeigu vieno iš jų atsiradimas nekeičia kito atsiradimo tikimybės. Kitu atveju įvykiai A ir B vadinami priklausomais.