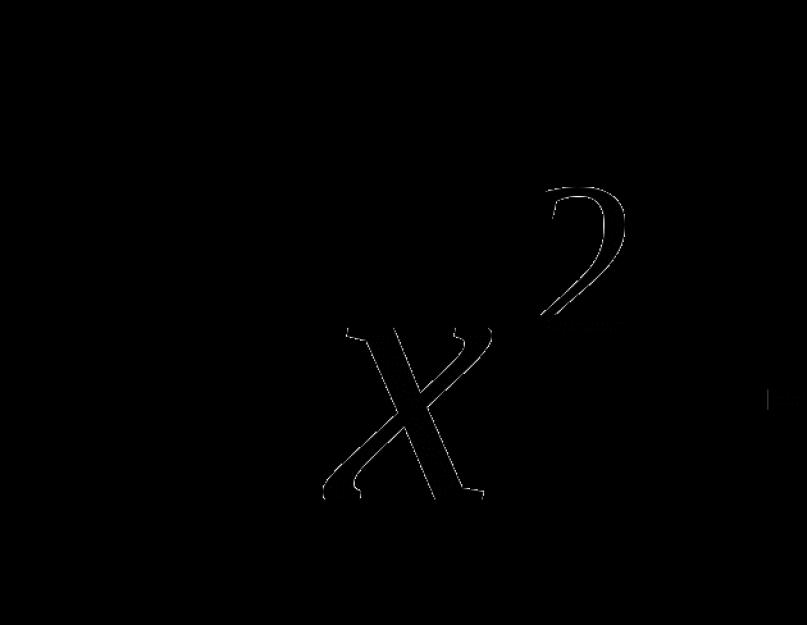Sažetak lekcije

„Metode rješenja iracionalne jednačine»

11. razred fizičko-matematičkog profila.

Zelenodolsky opštinski okrug RT"

Valieva S.Z.

Tema lekcije: Metode rješavanja iracionalnih jednačina

Svrha lekcije: 1. Istražite razne načine rješenja iracionalnih jednačina.

1. 
   Razviti sposobnost generalizacije, pravilnog odabira metoda za rješavanje iracionalnih jednačina.
2. 
   Razvijati samostalnost, obrazovati govornu pismenost

Vrsta lekcije: seminar.
Plan lekcije:

1. 
   Organiziranje vremena
2. 
   Učenje novog gradiva
3. 
   Sidrenje
4. 
   Zadaća
5. 
   Sažetak lekcije

Tokom nastave
I. Vrijeme organizacije: poruka teme lekcije, svrha lekcije.

U prethodnoj lekciji razmatrali smo rješavanje iracionalnih jednadžbi koje sadrže kvadratne korijene njihovim kvadriranjem. U ovom slučaju dobijamo jednačinu posledice, koja ponekad dovodi do pojave stranih korena. A onda je obavezan dio rješavanja jednadžbe provjera korijena. Razmotrili smo i rješavanje jednadžbi koristeći definiciju kvadratnog korijena. U ovom slučaju, provjera se može izostaviti. Međutim, prilikom rješavanja jednačina nije uvijek potrebno odmah prijeći na „slijepu“ primjenu algoritama za rješavanje jednačine. U zadacima Jedinstvenog državnog ispita postoji dosta jednadžbi, pri rješavanju kojih je potrebno odabrati metodu rješenja koja vam omogućava da lakše, brže rješavate jednadžbe. Stoga je neophodno poznavati i druge metode rješavanja iracionalnih jednačina, sa kojima ćemo se danas upoznati. Prethodno je razred bio podijeljen u 8 kreativnih grupa, a dobili su konkretne primjere kako bi otkrili suštinu određene metode. Dajemo im riječ.

II. Učenje novog gradiva.

Iz svake grupe 1 učenik objašnjava djeci kako se rješavaju iracionalne jednačine. Cijeli razred sluša i bilježi svoju priču.

1 način. Uvođenje nove varijable.

Riješite jednačinu: (2x + 3) 2 - 3

4x 2 + 12x + 9 - 3

4x 2 - 8x - 51 - 3

, t ≥0

x 2 - 2x - 6 \u003d t 2;

4t 2 – 3t – 27 = 0

x 2 - 2x - 15 \u003d 0

x 2 - 2x - 6 \u003d 9;

Odgovor: -3; 5.

2 way. ODZ istraživanja.

riješiti jednačinu

ODZ:


x = 2. Provjerom se uvjeravamo da je x = 2 korijen jednadžbe.

3 way. Množenje obje strane jednačine konjugiranim faktorom.

+
(pomnožite obje strane sa -
)

x + 3 - x - 8 \u003d 5 (-)

2=4, dakle x=1. Provjerom smo uvjereni da je x \u003d 1 korijen ove jednadžbe.

4 way. Redukcija jednadžbe na sistem uvođenjem varijable.

riješiti jednačinu

Neka je = u,
=v.

Dobijamo sistem:

Rešimo metodom zamene. Dobijamo u = 2, v = 2. Dakle,

dobijamo x = 1.

Odgovor: x = 1.

5 način. Odabir punog kvadrata.

riješiti jednačinu

Otvorimo module. Jer -1≤cos0.5x≤1, zatim -4≤cos0.5x-3≤-2, dakle . Isto tako,

Tada dobijamo jednačinu

x = 4πn, nZ.

Odgovor: 4πn, nZ.

6 način. Metoda ocjenjivanja

riješiti jednačinu

ODZ: x 3 - 2x 2 - 4x + 8 ≥ 0, po definiciji, desna strana -x 3 + 2x 2 + 4x - 8 ≥ 0

dobijamo
one. x 3 - 2x 2 - 4x + 8 = 0. Rješavajući jednačinu faktoringom, dobijamo x = 2, x = -2

Metoda 7: Korištenje svojstava monotonosti funkcija.

Riješite jednačinu. Funkcije se striktno povećavaju. Zbir rastućih funkcija raste i ova jednadžba ima najviše jedan korijen. Odabirom nalazimo x = 1.

8 način. Upotreba vektora.

Riješite jednačinu. ODZ: -1≤h≤3.

Neka vektor
. Skalarni proizvod vektori - da lijeva strana. Nađimo proizvod njihovih dužina. Ovo je prava strana. Imam
, tj. vektori a i b su kolinearni. Odavde
. Kvadratirajmo obje strane. Rješavajući jednadžbu, dobivamo x = 1 i x =
.

1. 
   Konsolidacija.(svaki učenik dobija nastavni listić)

Prednji usmeni rad

Pronađite ideju za rješavanje jednačina (1-10)

1.
(ODZ - )

2.
x = 2

3. x 2 - 3x +
(zamjena)

4. (izbor punog kvadrata)

5.
(Svođenje jednačine na sistem uvođenjem varijable.)

6.
(množenjem sa spojnim izrazom)

7.
jer
. Ova jednadžba nema korijen.

8. Jer svaki član nije negativan, izjednačavamo ih sa nulom i rješavamo sistem.

9. 3

10. Pronađite korijen jednačine (ili proizvod korijena, ako ih ima nekoliko) jednadžbe.

Napisano samostalan rad nakon čega slijedi verifikacija

riješiti jednačine pod brojevima 11,13,17,19

Riješite jednačine:

12. (x + 6) 2 -

14.

Metoda ocjenjivanja

Korištenje svojstava monotonosti funkcija.

Upotreba vektora.

1. 
   Koja od ovih metoda se koristi za rješavanje drugih vrsta jednačina?
2. 
   Koja od ovih metoda vam se najviše dopala i zašto?

1. 
   Domaći zadatak: Riješiti preostale jednačine.

Bibliografija:

1. 
   Algebra i početak matematičke analize: udžbenik. za 11 ćelija. opšte obrazovanje institucije / S.M. Nikolsky, M.K. Potapov, N.N. Reshetnikov, A.V. Shevkin. M: Prosvetljenje, 2009

1. 
   Didaktički materijali iz algebre i principi analize za 11. razred /B.M. Ivlev, S.M. Sahakyan, S.I. Schwarzburd. – M.: Prosvjeta, 2003.
2. 
   Mordkovich A. G. Algebra i počeci analize. 10 - 11 ćelija: Zadatak za opšte obrazovanje. institucije. – M.: Mnemosyne, 2000.
3. 
   Ershova A. P., Goloborodko V. V. Nezavisni i test papiri iz algebre i počeci analize za 10-11 razred. – M.: Ileksa, 2004
4. 
   KIM USE 2002 - 2010

6. Algebarski simulator. A.G. Merzlyak, V.B. Polonsky, M.S. Yakir. Priručnik za školarce i polaznike. Moskva.: "Ileksa" 2001.
7. Jednačine i nejednačine. Nestandardne metode rješenja. edukativni - Toolkit. 10 - 11 časova. S.N. Oleinik, M.K. Potapov, P. I. Pasichenko. Moskva. "Drofa". 2001

Vaša privatnost nam je važna. Iz tog razloga smo razvili Politiku privatnosti koja opisuje kako koristimo i pohranjujemo vaše podatke. Molimo pročitajte našu politiku privatnosti i javite nam ako imate pitanja.

Prikupljanje i korištenje ličnih podataka

Lični podaci odnose se na podatke koji se mogu koristiti za identifikaciju ili kontaktiranje određene osobe.

Od vas se može tražiti da unesete svoje lične podatke u bilo koje vrijeme kada nas kontaktirate.

U nastavku su navedeni neki primjeri vrsta ličnih podataka koje možemo prikupljati i kako ih možemo koristiti.

Koje lične podatke prikupljamo:

• Kada podnesete prijavu na stranici, možemo prikupljati različite informacije, uključujući vaše ime, broj telefona, adresu Email itd.

Kako koristimo vaše lične podatke:

• Lični podaci koje prikupljamo omogućavaju nam da vas kontaktiramo i informiramo o jedinstvenim ponudama, promocijama i drugim događajima i nadolazećim događajima.
• S vremena na vrijeme možemo koristiti vaše lične podatke kako bismo vam poslali važna obavještenja i komunikacije.
• Lične podatke možemo koristiti i za interne svrhe, kao što su provođenje revizija, analiza podataka i različita istraživanja kako bismo poboljšali usluge koje pružamo i dali vam preporuke u vezi s našim uslugama.
• Ako učestvujete u nagradnoj igri, natjecanju ili sličnom poticaju, možemo koristiti informacije koje nam date za upravljanje takvim programima.

Otkrivanje trećim licima

Podatke primljene od vas ne otkrivamo trećim licima.

Izuzeci:

• Po potrebi - u skladu sa zakonom, sudski nalog, u sudskim postupcima, i/ili na osnovu javnih zahtjeva ili zahtjeva od vladine agencije na teritoriji Ruske Federacije - otkrijte svoje lične podatke. Takođe možemo otkriti informacije o vama ako utvrdimo da je takvo otkrivanje neophodno ili prikladno iz razloga sigurnosti, provođenja zakona ili drugih razloga javnog interesa.
• U slučaju reorganizacije, spajanja ili prodaje, možemo prenijeti lične podatke koje prikupimo relevantnom trećem licu nasljedniku.

Zaštita ličnih podataka

Poduzimamo mjere opreza - uključujući administrativne, tehničke i fizičke - da zaštitimo vaše osobne podatke od gubitka, krađe i zloupotrebe, kao i od neovlaštenog pristupa, otkrivanja, izmjene i uništenja.

Održavanje vaše privatnosti na nivou kompanije

Kako bismo osigurali da su vaši lični podaci sigurni, našim zaposlenima komuniciramo o privatnosti i sigurnosnoj praksi i striktno provodimo praksu privatnosti.

Rješenje iracionalnih jednačina.

U ovom članku ćemo govoriti o načinima rješavanja problema najjednostavnije iracionalne jednadžbe.

Iracionalna jednadžba naziva se jednadžba koja sadrži nepoznatu pod predznakom korijena.

Pogledajmo dvije vrste iracionalne jednačine, koji su na prvi pogled vrlo slični, a zapravo se međusobno jako razlikuju.

(1)

(2)

U prvoj jednačini vidimo da je nepoznato pod znakom korena trećeg stepena. Možemo uzeti čudan korijen negativan broj, dakle, u ovoj jednačini nema ograničenja ni na izraz pod predznakom korijena ni na izraz na desnoj strani jednačine. Možemo podići obje strane jednadžbe na treći stepen da bismo se riješili korijena. Dobijamo ekvivalentnu jednačinu:

Kada podižemo desnu i lijevu stranu jednačine na neparan stepen, ne možemo se bojati dobijanja stranih korijena.

Primjer 1. Hajde da riješimo jednačinu

Podignimo obje strane jednadžbe na treći stepen. Dobijamo ekvivalentnu jednačinu:

Pomaknimo sve pojmove u jednom smjeru i izvadimo x iz zagrada:

Svaki faktor izjednačimo sa nulom, dobijemo:

Odgovor: (0;1;2)

Pogledajmo pobliže drugu jednačinu: . Na lijevoj strani jednadžbe je kvadratni korijen, koji uzima samo nenegativne vrijednosti. Dakle, da bi jednačina imala rješenja, desna strana također mora biti nenegativna. Stoga je na desnoj strani jednačine postavljen sljedeći uvjet:

Naslov="(!LANG:g(x)>=0"> - это !} uslov za postojanje korena.

Da biste riješili jednačinu ove vrste, trebate kvadrirati obje strane jednačine:

(3)

Kvadriranje može uvesti strane korijene, pa su nam potrebne jednadžbe:

Title="(!LANG:f(x)>=0"> (4)!}

Međutim, nejednakost (4) proizlazi iz uvjeta (3): ako je kvadrat nekog izraza na desnoj strani jednakosti, a kvadrat bilo kojeg izraza može imati samo nenegativne vrijednosti, tada i lijeva strana mora biti ne -negativan. Dakle, uvjet (4) automatski slijedi iz uvjeta (3) i našeg jednačina je ekvivalentno sistemu:

Title="(!LANG:delim(lbrace)(matrix(2)(1)((f(x)=g^2((x))) (g(x)>=0) ))( )">!}

Primjer 2. Rešimo jednačinu:

.

Pređimo na ekvivalentan sistem:

Title="(!LANG:delim(lbrace)(matrix(2)(1)((2x^2-7x+5=((1-x))^2) (1-x>=0) ))( )">!}

Rješavamo prvu jednačinu sistema i provjeravamo koji korijeni zadovoljavaju nejednačinu.

Nejednakost title="(!LANG:1-x>=0">удовлетворяет только корень !}

Odgovor: x=1

Pažnja! Ako u procesu rješavanja kvadriramo obje strane jednadžbe, onda moramo zapamtiti da se mogu pojaviti strani korijeni. Stoga, ili se trebate prebaciti na ekvivalentni sistem, ili na kraju rješenja PROVJERITE: pronađite korijene i zamijenite ih u originalnu jednačinu.

Primjer 3. Rešimo jednačinu:

Da bismo riješili ovu jednačinu, također moramo kvadrirati obje strane. Nemojmo se zamarati ODZ-om i uvjetom postojanja korijena u ovoj jednadžbi, već ćemo jednostavno na kraju rješenja provjeriti.

Kvadirajmo obje strane jednadžbe:

Prilikom izučavanja algebre studenti se susreću sa mnogo vrsta jednačina. Među onima koji su najjednostavniji mogu se navesti linearni koji sadrže jednu nepoznatu. Ako se varijabla u matematičkom izrazu podigne na određeni stepen, onda se jednačina naziva kvadratna, kubična, bikvadratna itd. Ovi izrazi mogu sadržavati racionalne brojeve. Ali postoje i iracionalne jednačine. Razlikuju se od ostalih po prisutnosti funkcije u kojoj je nepoznato pod znakom radikala (to jest, čisto izvana, varijabla se ovdje može vidjeti napisana pod kvadratnim korijenom). Rješavanje iracionalnih jednačina ima svoje karakteristike. Prilikom izračunavanja vrijednosti varijable da bi se dobio tačan odgovor, one se moraju uzeti u obzir.

"Neizrecivo riječima"

Nije tajna da su drevni matematičari uglavnom radili s racionalnim brojevima. To uključuje, kao što znate, cijele brojeve, izražene kroz obične i decimalne periodične razlomke, predstavnike ove zajednice. Međutim, naučnici Bliskog i Bliskog istoka, kao i Indije, razvijajući trigonometriju, astronomiju i algebru, takođe su naučili da rešavaju iracionalne jednačine. Na primjer, Grci su poznavali takve količine, ali, stavljajući ih u verbalnu formu, koristili su koncept "alogos", što je značilo "neiskazivo". Nešto kasnije, Evropljani su, oponašajući ih, takve brojeve nazvali "gluhim". Oni se razlikuju od svih ostalih po tome što se mogu predstaviti samo u obliku beskonačnog neperiodnog razlomka, čiji je konačni numerički izraz jednostavno nemoguće dobiti. Stoga se takvi predstavnici područja brojeva češće pišu u obliku brojeva i znakova kao neki izraz koji se nalazi ispod korijena drugog ili više.

Na osnovu prethodnog, pokušaćemo da definišemo iracionalnu jednačinu. Takvi izrazi sadrže takozvane "neizrazive brojeve", napisane znakom kvadratnog korijena. Mogu biti sve vrste prilično složenih opcija, ali u svojim najjednostavniji oblik izgleda kao na slici ispod.

Počevši rješavati iracionalne jednadžbe, prije svega je potrebno izračunati površinu dozvoljene vrijednosti varijabla.

Da li izraz ima smisla?

Potreba za provjerom dobijenih vrijednosti proizlazi iz svojstava.Kao što je poznato, takav izraz je prihvatljiv i ima bilo kakvo značenje samo pod određenim uslovima. U slučajevima parnog korijena, svi radikalni izrazi moraju biti pozitivni ili jednaki nuli. Ako ovaj uslov nije ispunjen, onda se prikazana matematička notacija ne može smatrati smislenom.

Dajemo konkretan primjer kako riješiti iracionalne jednadžbe (na slici ispod).

AT ovaj slučaj Očigledno je da ovi uslovi ne mogu biti zadovoljeni ni za jednu vrijednost koju uzima željena vrijednost, jer se ispostavlja da je 11 ≤ x ≤ 4. To znači da samo Ø može biti rješenje.

Metoda analize

Iz navedenog postaje jasno kako riješiti neke vrste iracionalnih jednačina. Evo na efikasan način može biti jednostavna analiza.

Navodimo niz primjera koji to opet jasno pokazuju (na fotografiji ispod).

U prvom slučaju, nakon pažljivog razmatranja izraza, odmah postaje krajnje jasno da on ne može biti istinit. Zaista, na kraju krajeva, na lijevoj strani jednakosti treba dobiti pozitivan broj, koji ni na koji način ne može biti jednak -1.

U drugom slučaju, zbir dva pozitivna izraza može se smatrati jednakim nuli samo kada je x - 3 = 0 i x + 3 = 0 u isto vrijeme. Opet, ovo je nemoguće. I tako, u odgovoru treba ponovo napisati Ø.

Treći primjer je vrlo sličan prethodnom. Zaista, ovdje uvjeti ODZ zahtijevaju da bude zadovoljena sljedeća apsurdna nejednakost: 5 ≤ x ≤ 2. I takva jednačina na sličan način ne može imati zdrava rješenja.

Neograničeno zumiranje

Priroda iracionalnog može se najjasnije i najpotpunije objasniti i spoznati samo kroz beskonačan niz decimalnih brojeva. I konkretno odličan primjer od članova ove porodice je pi. Ne bez razloga, pretpostavlja se da je ova matematička konstanta poznata od davnina, da se koristi za izračunavanje obima i površine kruga. No, među Evropljanima, prvi su ga u praksi primijenili Englez William Jones i Švicarac Leonhard Euler.

Ova konstanta nastaje na sljedeći način. Ako uporedimo najrazličitije opsege, onda je omjer njihovih duljina i promjera nužno jednak istom broju. Ovo je pi. Ako ga izrazimo kroz običan razlomak, otprilike ćemo dobiti 22/7. To je prvi učinio veliki Arhimed, čiji je portret prikazan na gornjoj slici. Zbog toga je sličan broj dobio i njegovo ime. Ali ovo nije eksplicitna, već približna vrijednost možda najnevjerovatnijeg broja. Briljantni naučnik je pronašao željenu vrijednost sa tačnošću od 0,02, ali, u stvari, ova konstanta nema stvarnu vrijednost, već se izražava kao 3,1415926535... To je beskonačan niz brojeva, koji se neograničeno približava određenoj mitskoj vrijednosti.

Kvadratura

Ali da se vratimo na iracionalne jednadžbe. Da biste pronašli nepoznato, u ovom slučaju se vrlo često pribjegava jednostavna metoda: kvadrat na obje strane postojeće jednakosti. Ova metoda obično daje dobre rezultate. Ali treba uzeti u obzir podmuklost iracionalnih vrijednosti. Svi korijeni dobiveni kao rezultat moraju se provjeriti, jer možda nisu prikladni.

Ali nastavimo s razmatranjem primjera i pokušajmo pronaći varijable na novopredloženi način.

Uopće nije teško, koristeći Vietinu teoremu, pronaći željene vrijednosti veličina nakon što smo, kao rezultat određenih operacija, formirali kvadratna jednačina. Ovdje se ispostavilo da će među korijenima biti 2 i -19. Međutim, prilikom provjere, zamjene dobivenih vrijednosti u originalni izraz, možete se uvjeriti da nijedan od ovih korijena nije prikladan. Ovo je uobičajena pojava u iracionalnim jednačinama. To znači da naša dilema opet nema rješenja, a u odgovoru treba navesti prazan skup.

Složeniji primjeri

U nekim slučajevima potrebno je kvadrirati obje strane izraza ne jednom, već nekoliko puta. Razmotrite primjere gdje je gore navedeno potrebno. Oni se mogu vidjeti u nastavku.

Nakon što ste dobili korijene, ne zaboravite ih provjeriti, jer se mogu pojaviti dodatni. Trebalo bi objasniti zašto je to moguće. Prilikom primjene takve metode na neki način dolazi do racionalizacije jednačine. Ali, oslobađajući se korijena koji su nam nepoželjni, koji nas sprečavaju da izvodimo aritmetičke operacije, mi, takoreći, proširujemo postojeći raspon vrijednosti, što je (kao što možete razumjeti) ispunjeno posljedicama. Predviđajući ovo, vršimo provjeru. U ovom slučaju postoji šansa da se uvjerite da samo jedan od korijena odgovara: x = 0.

Sistemi

Šta učiniti u slučajevima kada je potrebno riješiti sisteme iracionalnih jednačina, a imamo ne jednu, već dvije cijele nepoznanice? Ovdje postupamo na isti način kao u običnim slučajevima, ali uzimajući u obzir gornja svojstva ovih matematičkih izraza. I u svakom novom zadatku, naravno, treba primijeniti kreativan pristup. Ali, opet, bolje je uzeti u obzir sve konkretan primjer ispod. Ovdje nije potrebno samo pronaći varijable x i y, već i navesti njihov zbir u odgovoru. Dakle, postoji sistem koji sadrži iracionalne količine (pogledajte sliku ispod).

Kao što vidite, takav zadatak nije natprirodno težak. Samo treba biti pametan i pogoditi da je lijeva strana prve jednadžbe kvadrat zbira. Slični zadaci se nalaze na ispitu.

Iracionalno u matematici

Svaki put, potreba za stvaranjem novih tipova brojeva pojavila se za čovječanstvo kada mu je nedostajalo „prostora“ za rješavanje nekih jednačina. Iracionalni brojevi nisu izuzetak. Kao što svedoče činjenice iz istorije, prvi put su veliki mudraci na to skrenuli pažnju još pre naše ere, u 7. veku. To je uradio matematičar iz Indije, poznat kao Manava. Jasno je shvatio da je nemoguće izvući korijen iz nekih prirodnih brojeva. Na primjer, ovo uključuje 2; 17 ili 61, kao i mnoge druge.

Jedan od Pitagorejaca, mislilac po imenu Hipas, došao je do istog zaključka, pokušavajući da izvrši proračune sa numeričkim izrazima stranica pentagrama. Otkrivši matematičke elemente koji se ne mogu numerički izraziti i nemaju svojstva običnih brojeva, toliko je razljutio kolege da je bačen u more. Činjenica je da su drugi pitagorejci njegovo razmišljanje smatrali pobunom protiv zakona univerzuma.

Radikalni znak: evolucija

Znak korijena za izražavanje numeričke vrijednosti "gluhih" brojeva počeo je da se koristi u rješavanju iracionalnih nejednačina i jednačina daleko od odmah. Po prvi put, evropski, a posebno italijanski, matematičari su počeli da razmišljaju o radikalu oko 13. veka. Istovremeno su došli na ideju da za oznaku koriste latinicu R. No, njemački matematičari su u svojim radovima postupili drugačije. Više im se dopalo slovo V. U Njemačkoj su se ubrzo proširile oznake V (2), V (3), koje su trebale izraziti kvadratni korijen od 2, 3 itd. Kasnije su se umiješali Holanđani i promijenili predznak radikala. I Rene Descartes je završio evoluciju, dovodeći znak kvadratnog korijena do modernog savršenstva.

Oslobađanje od iracionalnog

Iracionalne jednadžbe i nejednačine mogu uključivati ​​varijablu ne samo ispod predznaka kvadratnog korijena. Može biti bilo kog stepena. Najčešći način da ga se riješite je podizanje obje strane jednadžbe na odgovarajući stepen. Ovo je glavna radnja koja pomaže u operacijama s iracionalnim. Radnje u parnim slučajevima se ne razlikuju posebno od onih koje smo ranije analizirali. Ovdje treba uzeti u obzir uslove za nenegativnost radikalnog izraza, a takođe je na kraju rješenja potrebno izdvojiti vanjske vrijednosti varijabli na način koji je prikazan u već razmatrani primjeri.

Od dodatnih transformacija koje pomažu u pronalaženju tačnog odgovora, često se koristi množenje izraza konjugatom, a često je potrebno uvesti i novu varijablu, što olakšava rješenje. U nekim slučajevima, za pronalaženje vrijednosti nepoznanica, preporučljivo je koristiti grafove.