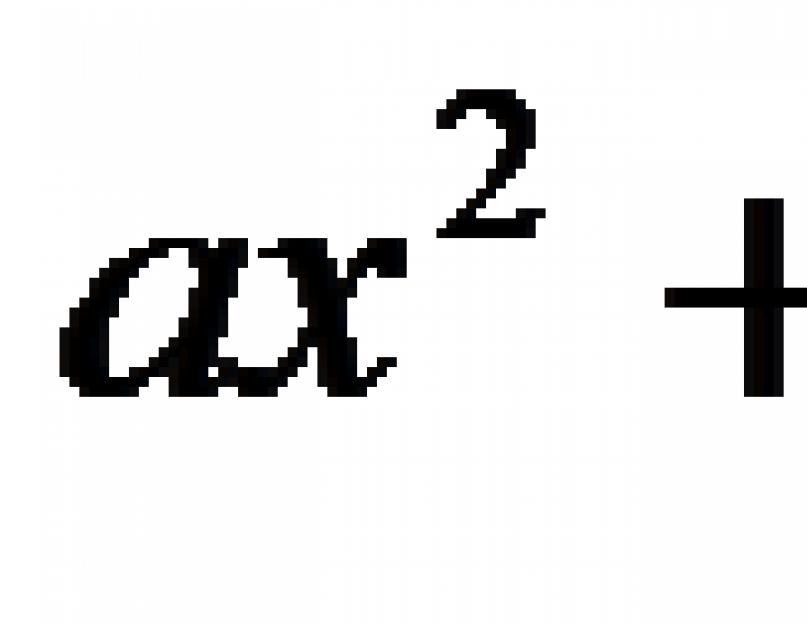عمل بحثي

حول الموضوع

"طرق الحل المعادلات التربيعية »

إجراء:
المجموعة 8 فئة "G"

مدير العمل:
بنكوفسكايا ماريا ميخائيلوفنا

أهداف وغايات المشروع.

1. أظهر أن الرياضيات ، مثل أي علم آخر ، لديها ما يكفي من الألغاز التي لم يتم حلها.
2. التأكيد على أن علماء الرياضيات يتميزون بالتفكير غير القياسي. وأحيانًا الفطنة والحدس عالم رياضيات جيدهي ببساطة مذهلة!
3. أظهر أن محاولة حل المعادلات التربيعية ساهمت في تطوير مفاهيم وأفكار جديدة في الرياضيات.
4. تعلم كيفية العمل مع مصادر مختلفة من المعلومات.
5. متابعة عمل بحثيالرياضيات

مراحل البحث

1. تاريخ ظهور المعادلات التربيعية.

2. تعريف المعادلة التربيعية وأنواعها.

3. حل المعادلات التربيعية باستخدام صيغة التمييز.

4. فرانسوا فيت ونظريته.

5. خواص المعاملات لإيجاد جذور المعادلة التربيعية بسرعة.

6. التوجه العملي.

من خلال المعادلات والنظريات

لقد قمت بحل الكثير من المشاكل.

(تشوسر ، شاعر إنجليزي، العصور الوسطى.)

المسرح. تاريخ ظهور المعادلات التربيعية.

كانت الحاجة إلى حل المعادلات ليس فقط من الدرجة الأولى ، ولكن أيضًا من الدرجة الثانية ، التي تعود إلى العصور القديمة بسبب الحاجة إلى حل المشكلات المتعلقة بإيجاد المناطق قطع ارضوأعمال الحفر ذات الطبيعة العسكرية ، وكذلك مع تطور علم الفلك والرياضيات نفسها.

كان البابليون قادرين على حل المعادلات التربيعية حوالي عام 2000 قبل الميلاد. تتطابق قاعدة حل هذه المعادلات ، المنصوص عليها في النصوص البابلية ، بشكل أساسي مع القواعد الحديثة ، لكن من غير المعروف كيف جاء البابليون لإيجاد القاعدة. تقريبًا كل النصوص المسمارية التي تم العثور عليها حتى الآن لا تقدم سوى مشاكل تتعلق بالحلول المذكورة في شكل وصفات ، مع عدم وجود إشارة إلى كيفية العثور عليها.

على الرغم من مستوى عالتطور الجبر في بابل ، في النصوص المسمارية لا يوجد مفهوم للرقم السالب والطرق العامة لحل المعادلات التربيعية.

يحتوي "الحساب" لديوفانتوس على سلسلة منهجية من المسائل مصحوبة بتفسيرات وتحل بصياغة معادلات بدرجات مختلفة، لكنها تفتقر إلى شرح منهجي للجبر.

تم العثور بالفعل على مشاكل المعادلات التربيعية في الأطروحات الفلكية "Aryabhattiam" ، التي جمعت في عام 499. عالم الرياضيات والفلك الهندي أرياباتا. عالم هندي آخر ، Brahmagupta (القرن السابع) ، شرح قاعدة عامةحلول المعادلات التربيعية المختزلة إلى شكل أساسي واحد:

تعطي أطروحة الخورزمي الجبرية تصنيفًا للمعادلات الخطية والتربيعية. المؤلف لديه 6 أنواع من المعادلات. للخوارزمي الذي لا يعرف أرقام سالبة، شروط كل معادلة هي إضافات ، وليست مطروحات فرعية. في الوقت نفسه ، لا يتم أخذ المعادلات التي ليس لها حلول إيجابية في الاعتبار بشكل متعمد ؛ عند حل معادلة تربيعية غير مكتملة ، لا يأخذ الخوارزمي ، مثل جميع العلماء قبل القرن السابع عشر ، في الاعتبار الحل الصفري.

إن أطروحة الخوارزمي هي أول كتاب وصل إلينا ، حيث يتم عرض تصنيف المعادلات التربيعية والصيغ لحلها بشكل منهجي.

تم وضع صيغ حل المعادلات التربيعية على نموذج الخوارزمي في أوروبا لأول مرة في كتاب العداد ، الذي كتبه عالم الرياضيات الإيطالي ليوناردو فيبوناتشي عام 1202. يتميز هذا العمل الضخم باكتماله ووضوح عرضه. طور المؤلف بشكل مستقل بعض الأساليب الجبرية الجديدة لحل المشكلات ، وكان أول من اقترب من إدخال الأعداد السالبة في أوروبا. ساهم كتابه في انتشار المعرفة الجبرية ليس فقط في إيطاليا ، ولكن أيضًا في ألمانيا وفرنسا ودول أوروبية أخرى. مرت العديد من المشكلات من كتاب العداد إلى جميع الكتب المدرسية الأوروبية تقريبًا في القرنين السادس عشر والسابع عشر والثامن عشر جزئيًا.

قاعدة عامة لحل المعادلات التربيعية مختزلة إلى صيغة واحدة أساسية مع كل المجموعات الممكنة من العلامات المعاملات ب ، جتمت صياغته في أوروبا فقط في عام 1544 بواسطة M. Stiefel.

اشتقاق صيغة حل المعادلة التربيعية في نظرة عامةفييت ، لكن فييت أدركت الجذور الإيجابية فقط. كان علماء الرياضيات الإيطاليون Tartaglia و Cardano و Bombelli من بين الأوائل في القرن السادس عشر الذين أخذوا في الاعتبار ليس فقط الجذور الإيجابية ، ولكن أيضًا الجذور السلبية. فقط في القرن السابع عشر ، وبفضل أعمال جيرارد وديكارت ونيوتن وعلماء آخرين ، اتخذت طريقة حل المعادلات التربيعية شكلاً حديثًا.

يتحول:

تم العثور على مشاكل في المعادلات التربيعية بالفعل في 499.

في الهند القديمةتم توزيع المسابقات العامة في حل المشكلات الصعبة - أولمبيادز .

© 2015-2019 الموقع
جميع الحقوق تنتمي إلى مؤلفيها. لا يدعي هذا الموقع حقوق التأليف ، ولكنه يوفر الاستخدام المجاني.
تاريخ إنشاء الصفحة: 2016-04-11

ممثلو الحضارات المختلفة: مصر القديمةبابل القديمة اليونان القديمة، الهند القديمة، الصين القديمة، شرق العصور الوسطى ، أتقنت أوروبا تقنيات حل المعادلات التربيعية.

لأول مرة ، تمكن علماء الرياضيات في مصر القديمة من حل معادلة تربيعية. تحتوي إحدى البرديات الرياضية على المشكلة:

"ابحث عن جوانب حقل له شكل مستطيل ، إذا كانت مساحته 12 ، و- الأطوال تساوي العرض." تقول البردية: "طول الحقل 4".

مرت آلاف السنين ، دخلت الأرقام السالبة في الجبر. بحل المعادلة x² = 16 ، نحصل على رقمين: 4 ، -4.

بالطبع ، في المسألة المصرية ، نأخذ X = 4 ، لأن طول الحقل يمكن أن يكون فقط قيمة موجبة.

تشير المصادر التي وصلت إلينا إلى أن العلماء القدماء امتلكوا بعض الأساليب العامة لحل المشكلات بكميات غير معروفة. قاعدة حل المعادلات التربيعية ، المنصوص عليها في النصوص البابلية ، هي في الأساس نفس القاعدة الحديثة ، لكن من غير المعروف كيف "وصل البابليون إلى هذه النقطة". ولكن في كل نصوص البرديات والكتابة المسمارية تقريبًا ، يتم تقديم مشاكل الحلول فقط. قام المؤلفون أحيانًا فقط بتزويد حساباتهم العددية بتعليقات متوسطة مثل: "انظر!" ، "افعلها!" ، "لقد وجدت ذلك صحيحًا!".

كتب عالم الرياضيات اليوناني Diophantus وحل المعادلات التربيعية. لا يحتوي "الحساب" الخاص به على عرض منهجي للجبر ، ولكنه يحتوي على سلسلة منهجية من المسائل ، مصحوبة بتفسيرات وتحل عن طريق تجميع المعادلات بدرجات مختلفة.

تم العثور بالفعل على مهام تجميع المعادلات التربيعية في الأطروحة الفلكية "Aria-bhatiam" ، التي جمعتها في عام 499 عالم الرياضيات والفلك الهندي أريابهاتا.

حدد عالم هندي آخر Brahmagupta (القرن السابع) القاعدة العامة لحل المعادلات التربيعية للصيغة ax² + bx = c.

في الهند القديمة ، كانت المسابقات العامة في حل المشكلات الصعبة شائعة. في أحد الكتب الهندية القديمة عن مثل هذه المسابقات ، قيل ما يلي: "كما تشرق الشمس على النجوم بتألقها ، لذلك رجل عالميحجب مجد آخر في الجلسات العامة ويقترح ويحل المسائل الجبرية. غالبًا ما كانت المهمات ترتدي الشكل الشعري.

إليكم إحدى مشكلات عالم الرياضيات الهندي الشهير في القرن الثاني عشر. باسكارا:

قطيع من القردة الطرية

الأكل الجيد والاستمتاع.

الجزء الثامن منهم في الساحة كان مسليا في المقاصة.

واثنا عشر على طول الكروم ... بدأوا يقفزون معلقين ...​

كم عدد القردة

أخبرني ، في هذا القطيع؟

يشير حل Bhaskara إلى أنه كان على علم بالقيمة الثنائية لجذور المعادلات التربيعية.

تعود أقدم النصوص الرياضية الصينية التي وصلت إلينا إلى نهاية القرن الأول قبل الميلاد. قبل الميلاد. في القرن الثاني. قبل الميلاد. تمت كتابة الرياضيات في تسعة كتب. في وقت لاحق ، في القرن السابع ، تم تضمينه في مجموعة "عشر رسائل كلاسيكية" ، والتي تمت دراستها لعدة قرون. تشرح أطروحة "الرياضيات في تسعة كتب" كيفية استخراج الجذر التربيعي باستخدام صيغة مربع مجموع رقمين.

كانت تسمى الطريقة "تيان يوان" (حرفيا - "العنصر السماوي") - حيث أشار الصينيون إلى كمية غير معروفة.​

كان الدليل الأول لحل المشكلات ، والذي أصبح معروفًا على نطاق واسع ، هو عمل عالم بغداد في القرن التاسع. محمد بن موسى الخوارزمي. كلمة "الجبر" - مع مرور الوقت تحولت إلى كلمة مشهورة "الجبر" ، وأصبح تكوين الخوارزمي نفسه نقطة البدايةفي تطوير علم حل المعادلات. تعطي أطروحة الخورزمي الجبرية تصنيفًا للمعادلات الخطية والتربيعية. يسرد المؤلف ستة أنواع من المعادلات ، معربًا عنها على النحو التالي:

-المربعات جذور متساوية، هذا هو آه ² = ب س ؛

-المربعات عدد متساوٍ، هذا هو آه ² = ج ؛

-الجذور تساوي العدد، وهذا هو ، الفأس = ج ؛

-المربعات والأرقام تساوي الجذور، هذا هو آه ² + ج \ u003d ب س ؛

-المربعات والجذور تساوي العدد، هذا هو آه ² + bx \ u003d ج ​​؛

-الجذور والأرقام مربعة، أي bx + c = ax ²;

إن أطروحة الخوارزمي هي أول كتاب وصل إلينا ، حيث يتم تقديم تصنيف المعادلات التربيعية بشكل منهجي وتقديم الصيغ لحلها.

تم وضع صيغ حل المعادلات التربيعية على نموذج الخوارزمي في أوروبا لأول مرة في كتاب العداد ، الذي كتبه عالم الرياضيات الإيطالي ليوناردو فيبوناتشي عام 1202. طور المؤلف بشكل مستقل بعض الأمثلة الجبرية الجديدة لحل المشكلات وكان أول من اقترب من إدخال الأرقام السالبة في أوروبا. ساهم كتابه في انتشار المعرفة الجبرية ليس فقط في إيطاليا ، ولكن أيضًا في ألمانيا وفرنسا ودول أوروبية أخرى. تم تضمين العديد من المهام من كتاب العداد في جميع الكتب المدرسية الأوروبية تقريبًا في القرنين السادس عشر والسابع عشر. وجزء من القرن الثامن عشر.

القاعدة العامة لحل المعادلات التربيعية مختزلة إلى صيغة واحدة أساسية x ² + bx \ u003d c ، مع كل التوليفات الممكنة لعلامات المعاملين b و c ، صاغها M. Stiefel في أوروبا فقط في عام 1544.

يمتلك فييتا اشتقاقًا عامًا لصيغة حل المعادلة التربيعية ، لكنه أدرك أيضًا الجذور الإيجابية فقط. كان علماء الرياضيات الإيطاليون تارتاليا وكاردانو وبومبيلي من بين الأوائل في القرن السادس عشر. تأخذ في الاعتبار بالإضافة إلى الجذور الإيجابية والسلبية. فقط في القرن السابع عشر ، وبفضل أعمال جيرارد وديكارت ونيوتن وعلماء آخرين ، اتخذت طريقة حل المعادلات التربيعية شكلاً حديثًا.

​

​

مدرسة Kopyevskaya الثانوية الريفية

10 طرق لحل المعادلات التربيعية

الرأس: باتريكيفا غالينا أناتوليفنا ،

مدرس رياضيات

s.Kopyevo ، 2007

1. تاريخ تطور المعادلات التربيعية

1.1 المعادلات التربيعية في بابل القديمة

1.2 كيف قام ديوفانتوس بتجميع وحل المعادلات التربيعية

1.3 المعادلات التربيعية في الهند

1.4 المعادلات التربيعية في الخوارزمي

1.5 المعادلات التربيعية في أوروبا القرنين الثالث عشر والسابع عشر

1.6 حول نظرية فييتا

2. طرق حل المعادلات التربيعية

استنتاج

المؤلفات

1. تاريخ تطور المعادلات التربيعية

1.1 المعادلات التربيعية في بابل القديمة

كانت الحاجة إلى حل المعادلات ليس فقط من الدرجة الأولى ، ولكن أيضًا من الدرجة الثانية في العصور القديمة بسبب الحاجة إلى حل المشكلات المتعلقة بإيجاد مناطق الأرض وأعمال الحفر ذات الطبيعة العسكرية ، وكذلك تطوير علم الفلك و الرياضيات نفسها. كانت المعادلات التربيعية قادرة على حل حوالي 2000 قبل الميلاد. ه. البابليون.

بتطبيق تدوين جبري حديث ، يمكننا القول أنه في نصوصهم المسمارية توجد ، بالإضافة إلى النصوص غير المكتملة ، على سبيل المثال ، معادلات تربيعية كاملة:

X 2 + X = ¾; X 2 - X = 14,5

تتطابق قاعدة حل هذه المعادلات ، المنصوص عليها في النصوص البابلية ، بشكل أساسي مع القاعدة الحديثة ، لكن من غير المعروف كيف جاء البابليون إلى هذه القاعدة. تقريبًا كل النصوص المسمارية التي تم العثور عليها حتى الآن لا تقدم سوى مشاكل تتعلق بالحلول المذكورة في شكل وصفات ، مع عدم وجود إشارة إلى كيفية العثور عليها.

على الرغم من ارتفاع مستوى تطور علم الجبر في بابل ، إلا أن النصوص المسمارية تفتقر إلى مفهوم الرقم السالب والطرق العامة لحل المعادلات التربيعية.

1.2 كيف قام ديوفانتوس بتجميع وحل المعادلات التربيعية.

لا يحتوي حساب Diophantus 'الحسابي على عرض منهجي للجبر ، ولكنه يحتوي على سلسلة منهجية من المسائل ، مصحوبة بتفسيرات ويتم حلها عن طريق وضع معادلات بدرجات مختلفة.

عند تجميع المعادلات ، يختار Diophantus بمهارة المجهول لتبسيط الحل.

هنا ، على سبيل المثال ، هي إحدى مهامه.

المهمة 11."أوجد رقمين مع العلم أن مجموعهما 20 وحاصل ضربهما 96"

يجادل Diophantus على النحو التالي: ينتج عن حالة المشكلة أن الأرقام المرغوبة ليست متساوية ، لأنه إذا كانت متساوية ، فلن يكون ناتجها 96 ، بل 100. وهكذا ، سيكون أحدهم أكثر من نصف المجموع ، أي. 10 + سوالآخر أصغر أي 10's. الفرق بينهما 2x .

ومن هنا جاءت المعادلة:

(10 + س) (10 - س) = 96

100 - × 2 = 96

× 2-4 = 0 (1)

من هنا س = 2. أحد الأرقام المطلوبة هو 12 ، آخر 8 . المحلول س = -2بالنسبة إلى Diophantus غير موجود ، لأن الرياضيات اليونانية كانت تعرف الأعداد الموجبة فقط.

إذا حللنا هذه المشكلة باختيار أحد الأرقام المرغوبة باعتباره المجهول ، فسنصل إلى حل المعادلة

ص (20 - ص) = 96 ،

ص 2 - 20 ص + 96 = 0. (2)

من الواضح أن Diophantus يبسط الحل باختيار نصف فرق الأرقام المرغوبة على أنها غير معروفة ؛ تمكن من تقليل المشكلة إلى حل معادلة تربيعية غير مكتملة (1).

1.3 المعادلات التربيعية في الهند

تم العثور بالفعل على مشاكل المعادلات التربيعية في المسالك الفلكية "Aryabhattam" ، التي جمعت في 499 من قبل عالم الرياضيات والفلك الهندي Aryabhatta. حدد عالم هندي آخر ، Brahmagupta (القرن السابع) ، القاعدة العامة لحل المعادلات التربيعية التي تم تقليصها إلى شكل أساسي واحد:

آه 2+ ب س = ج ، أ> 0. (1)

في المعادلة (1) ، المعاملات ، باستثناء أ، يمكن أن تكون سلبية أيضًا. يتطابق حكم براهماغوبتا بشكل أساسي مع حكمنا.

في الهند القديمة ، كانت المسابقات العامة في حل المشكلات الصعبة شائعة. في أحد الكتب الهندية القديمة ، قيل ما يلي عن مثل هذه المسابقات: "عندما تشرق الشمس على النجوم بتألقها ، فإن الشخص المتعلم سوف يتفوق على مجد آخر في الاجتماعات العامة ، ويقترح ويحل المسائل الجبرية." غالبًا ما كانت ترتدي المهام في شكل شعري.

إليكم إحدى مشكلات عالم الرياضيات الهندي الشهير في القرن الثاني عشر. باسكارا.

المهمة 13.

"قطيع مرح من القرود واثنا عشر في الكروم ...

بعد أن أكل السلطة ، استمتع. بدأوا في القفز ، معلقين ...

الجزء الثامن منهم في مربع كم عدد القردة هناك ،

يلهون في المرج. أخبرني ، في هذا القطيع؟

يشير حل باسكارا إلى أنه كان على علم بالقيمة الثنائية لجذور المعادلات التربيعية (الشكل 3).

المعادلة المقابلة للمسألة 13 هي:

( x /8) 2 + 12 = x

يكتب باسكارا تحت ستار:

× 2 - 64 × = -768

ولتكملة الجهه اليسرىمن هذه المعادلة إلى المربع ، يضيف إلى كلا الجانبين 32 2 ، ثم الحصول على:

× 2 - 64 × + 32 2 = -768 + 1024 ،

(س - 32) 2 = 256 ،

س - 32 = ± 16 ،

× 1 = 16 ، × 2 = 48.

1.4 المعادلات التربيعية في الخوارزمي

تعطي أطروحة الخورزمي الجبرية تصنيفًا للمعادلات الخطية والتربيعية. يسرد المؤلف 6 أنواع من المعادلات ، معربًا عنها على النحو التالي:

1) "المربعات تساوي الجذور" ، أي الفأس 2 + ج = ب X.

2) "المربعات تساوي الرقم" ، أي الفأس 2 = ق.

3) "الجذور تساوي العدد" ، أي آه = ق.

4) "المربعات والأرقام تساوي الجذور" ، أي الفأس 2 + ج = ب X.

5) "المربعات والجذور تساوي العدد" ، أي آه 2+ bx = ق.

6) "الجذور والأرقام تساوي المربعات" ، أي bx + ج \ u003d فأس 2.

بالنسبة للخوارزمي ، الذي تجنب استخدام الأعداد السالبة ، فإن مصطلحات كل من هذه المعادلات هي عمليات الجمع ، وليس الطرح. في هذه الحالة ، من الواضح أن المعادلات التي ليس لها حلول إيجابية لا تؤخذ في الاعتبار. يحدد المؤلف طرق حل هذه المعادلات باستخدام طريقتي الجبر والمقبلة. قراراته ، بالطبع ، لا تتوافق تمامًا مع قراراتنا. ناهيك عن حقيقة أنها بلاغية بحتة ، وتجدر الإشارة ، على سبيل المثال ، إلى أنه عند حل معادلة تربيعية غير مكتملة من النوع الأول

الخوارزمي ، مثله مثل جميع علماء الرياضيات قبل القرن السابع عشر ، لا يأخذ في الحسبان الحل الصفري ، ربما لأنه لا يهم في مشاكل عملية محددة. عند حل المعادلات التربيعية الكاملة ، يحدد الخورزمي قواعد الحل ، ثم البراهين الهندسية ، باستخدام أمثلة عددية معينة.

المهمة 14."المربع والرقم 21 يساوي 10 جذور. ابحث عن الجذر " (بافتراض جذر المعادلة x 2 + 21 = 10x).

يتحول حل المؤلف إلى شيء كالتالي: اقسم عدد الجذور إلى النصف ، وستحصل على 5 ، واضرب 5 في نفسه ، واطرح 21 من الناتج ، ويتبقى 4. خذ جذر 4 ، وستحصل على 2. اطرح 2 من 5 ، أنت الحصول على 3 ، سيكون هذا هو الجذر المطلوب. أو أضف 2 إلى 5 ، ما يعطينا 7 ، فهذا أيضًا جذر.

تعتبر رسالة الخورزمي أول كتاب وصل إلينا ، حيث تم تحديد تصنيف المعادلات التربيعية بشكل منهجي وإعطاء الصيغ لحلها.

1.5 المعادلات التربيعية في أوروبا الثالث عشر - السابع عشر قرون

تم وضع صيغ حل المعادلات التربيعية على نموذج الخوارزمي في أوروبا لأول مرة في "كتاب العداد" ، الذي كتبه عالم الرياضيات الإيطالي ليوناردو فيبوناتشي عام 1202. يتميز هذا العمل الضخم ، الذي يعكس تأثير الرياضيات ، في كل من بلاد الإسلام واليونان القديمة ، بالاكتمال والوضوح في العرض. طور المؤلف بشكل مستقل بعض الأمثلة الجبرية الجديدة لحل المشكلات وكان أول من اقترب من إدخال الأرقام السالبة في أوروبا. ساهم كتابه في انتشار المعرفة الجبرية ليس فقط في إيطاليا ، ولكن أيضًا في ألمانيا وفرنسا ودول أوروبية أخرى. تم تمرير العديد من المهام من "كتاب العداد" إلى جميع الكتب المدرسية الأوروبية تقريبًا في القرنين السادس عشر والسابع عشر. وجزئيا الثامن عشر.

القاعدة العامة لحل المعادلات التربيعية المختزلة إلى شكل أساسي واحد:

× 2+ bx = مع

لجميع المجموعات الممكنة لعلامات المعاملات ب , معتمت صياغته في أوروبا فقط في عام 1544 بواسطة M. Stiefel.

لدى Vieta اشتقاق عام لصيغة حل المعادلة التربيعية ، لكن فييتا أدركت الجذور الإيجابية فقط. كان علماء الرياضيات الإيطاليون تارتاليا وكاردانو وبومبيلي من بين الأوائل في القرن السادس عشر. ضع في اعتبارك ، بالإضافة إلى الجذور الإيجابية والسلبية. فقط في القرن السابع عشر. بفضل عمل جيرارد وديكارت ونيوتن وآخرين طريقة العلماءحل المعادلات التربيعية يتخذ شكلًا حديثًا.

1.6 حول نظرية فييتا

النظرية التي تعبر عن العلاقة بين معاملات المعادلة التربيعية وجذورها ، التي تحمل اسم فيتا ، صاغها لأول مرة في عام 1591 على النحو التالي: "إذا ب + دمضروبا أ - أ 2 ، يساوي BD، ومن بعد أيساوي فيومتساو د ».

لفهم فييتا ، يجب على المرء أن يتذكر ذلك لكن، مثل أي حرف علة ، يعني بالنسبة له المجهول (لدينا X)، حروف العلة في، د- معاملات المجهول. بلغة الجبر الحديثة ، فإن صياغة فييتا أعلاه تعني: إذا

(أ + ب ) س - س 2 = أب ,

× 2 - (أ + ب ) x + أ ب = 0,

س 1 = أ ، س 2 = ب .

للتعبير عن العلاقة بين جذور المعادلات ومعاملاتها بالصيغ العامة المكتوبة باستخدام الرموز ، أسس فيت التوحيد في طرق حل المعادلات. ومع ذلك ، فإن رمزية فييتا لا تزال بعيدة كل البعد عن نظرة حديثة. لم يتعرف على الأرقام السالبة ، وبالتالي ، عند حل المعادلات ، لم يأخذ في الاعتبار سوى الحالات التي تكون فيها جميع الجذور موجبة.

2. طرق حل المعادلات التربيعية

المعادلات التربيعية هي الأساس الذي تقوم عليه مبنى مهيبالجبر. إيجاد المعادلات التربيعية تطبيق واسععند حل المعادلات والمتباينات المثلثية والأسية واللوغاريتمية وغير المنطقية والمتجاوزة. نعلم جميعًا كيفية حل المعادلات التربيعية من المدرسة (الصف الثامن) حتى التخرج.

الصفحة الرئيسية> تقرير

المدرسة الثانوية مذكرة التفاهم التي سميت على اسم الأبطال الاتحاد السوفياتي
سوتنيكوفا أ. و Shepeleva N.G.S Uritskoe

تقرير عن الموضوع:

"تاريخ الظهور

المعادلات التربيعية"

أُعدت بواسطة:إيزوتوفا جوليا
أمبليفا إلينا ،
شيبليف نيكولاي ،

دياتشينكو يوري.

يا رياضيات. لقرون ، أنت مغطى بالمجد ،

نجم كل النجوم الدنيوية.

أنت ملكة مهيبة

لا عجب في تعميد غاوس.

صارم ، منطقي ، مهيب ،

نحيف في الرحلة ، مثل السهم ،

مجدك الأبدي

على مر العصور ، نالت الخلود.

نحمد العقل البشري

أفعاله الأيدي السحرية,

أمل هذا العصر

ملكة كل العلوم الأرضية.

نريد أن نخبرك اليوم

تاريخ الحدوث

ما يجب أن يعرفه كل طالب

تاريخ المعادلات التربيعية.

إقليدس في القرن الثالث قبل الميلاد. ه. في "مبادئه" المكرس للجبر الهندسي الكتاب الثاني بأكمله ، والذي يحتوي على جميع المواد اللازمة لحل المعادلات التربيعية.

إقليدس (Eνκλειδηζ) ، عالم رياضيات يوناني قديم ، مؤلف أول رسالة نظرية في الرياضيات وصلت إلينا

المعلومات حول إقليدس نادرة للغاية. الشيء الوحيد الذي يمكن اعتباره موثوقًا هو ذلك النشاط العلميتدفقت في الإسكندرية في القرن الثالث قبل الميلاد. ه. إقليدس هو أول عالم رياضيات في مدرسة الإسكندرية. له الوظيفة الرئيسية"البدايات" (في الشكل اللاتيني - "العناصر") تحتوي على عرض للقياسات والقياس الفراغي وعدد من القضايا في نظرية الأعداد ؛ في ذلك لخص التطور السابق للرياضيات اليونانية وخلق الأساس مزيد من التطويرالرياضيات. مالك الحزين - عالم رياضيات ومهندس يوناني لأول مرة في اليونان في القرن الأول الميلادي. يعطي طريقة جبرية بحتة لحل المعادلة التربيعية.

مالك الحزين الاسكندريه؛ قوى. ن. هـ ، ميكانيكي وعالم رياضيات يوناني. وقت حياته غير مؤكد ، ومن المعروف فقط أنه اقتبس من أرخميدس (الذي توفي عام 212 قبل الميلاد) ، وهو نفسه نقله بابوس (300 م). في الوقت الحاضر ، الرأي السائد هو أنه عاش في القرن الأول. ن. ه. درس الهندسة والميكانيكا والهيدروستاتيك والبصريات. اخترع النموذج الأولي للمحرك البخاري وأدوات التسوية الدقيقة. أشهر الآلات الآلية كانت المسارح الأوتوماتيكية والنوافير وغيرها.وصف G. المزواة ، بالاعتماد على قوانين الإحصائيات والحركية ، وقدم وصفًا للرافعة ، والكتلة ، والمروحة ، والمركبات العسكرية. في علم البصريات ، صاغ قوانين انعكاس الضوء في الرياضيات - طرق قياس أهمها الأشكال الهندسية. أعمال G. الرئيسية هي Etrika و Pneumatics و Autopoietics و Mechanics (بالفرنسية ؛ تم حفظ العمل بالكامل باللغة العربية) ، Catoptics (علم المرايا ؛ محفوظ فقط في الترجمة اللاتينية) وآخرون.استخدم G. إنجازات أسلافه: إقليدس ، أرخميدس ، ستراتو من لامبساك. أسلوبه بسيط وواضح ، رغم أنه في بعض الأحيان مقتضب للغاية أو غير منظم. نشأ الاهتمام في كتابات ج. في القرن الثالث. ن. ه. علق الطلاب اليونانيون ثم البيزنطيون والعربيون على أعماله وترجموها.

ديوفانتوس- قام عالم يوناني في القرن الثالث الميلادي ، دون اللجوء إلى الهندسة ، بحل بعض المعادلات التربيعية بطريقة جبرية بحتة ، وتمت كتابة المعادلة نفسها وحلها في شكل رمزي

"سأخبرك كيف قام عالم الرياضيات اليوناني ديوفانتوس بتأليف وحل المعادلات التربيعية. وهنا على سبيل المثال من مهامه:"أوجد رقمين مع العلم أن مجموعهما 20 وحاصل ضربهما 96."

1. من حالة المشكلة يترتب على ذلك أن الأرقام المرغوبة ليست متساوية ، لأن إذا كانتا متساويتين ، فلن يكون ناتجهما 96 بل 100.

2. هكذا. واحد منهم سيكون أكثر من نصف مجموعهم ، أي. 10 + س ، والآخر أقل ، أي 10 - س.

3. الفرق بينهما هو 2x.

4. ومن هنا جاءت المعادلة (10 + س) * (10 - س) = 96

100 - س 2 = 96 × 2-4 = 0

5. الإجابة س = 2. أحد الأرقام المرغوبة هو 12 ،
أخرى - 8. الحل x = - 2 لـ Diophantus غير موجود ، لأن عرفت الرياضيات اليونانية الأرقام الموجبة فقط ". عرف Diophantus كيفية حل المعادلات المعقدة للغاية ، المستخدمة في المجهول تسميات الحروف، أدخل رمزًا خاصًا للحساب ، واختصارات الكلمات المستخدمة. بهاسكاري - عقارية- عالم رياضيات هندي في القرن الثاني عشر الميلادي. افتتح الطريقة العامةحلول المعادلات التربيعية.

دعنا نحلل إحدى مشاكل علماء الرياضيات الهنود ، على سبيل المثال ، مشكلة بهاسكارا:

"قطيع من القرود يستمتع بوقته: ثُمن العدد الإجمالي في مربع مرح في الغابة ، بينما يصرخ الاثنا عشر الباقي في أعلى التل. قل لي ، كم عدد القردة هناك؟ "

وتعليقًا على المشكلة ، أود أن أقول إن المعادلة (x / 8) 2 + 12 = x تتوافق مع المشكلة. يكتب Bhaskara كـ x 2 - 64x \ u003d - 768. بإضافة مربع 32 إلى كلا الجزأين ، ستأخذ المعادلة الشكل:

× 2 - 64 × + 32 2 = - 768 + 1024

(س - 32) 2 = 256

بعد استخراج الجذر التربيعي ، نحصل على: x - 32 = 16.

"في هذه القضية، يقول باسكارا ، - الوحدات السالبة للجزء الأول هي بحيث تكون وحدات الجزء الثاني أقل منها ، وبالتالي يمكن اعتبار الأخير موجبًا وسالبًا ، ونحصل على القيمة المزدوجة للمجهول: 48 و 16.

يجب أن نستنتج أن حل Bhaskara يشير إلى أنه كان على علم بالقيمة الثنائية لجذور المعادلات التربيعية.

يقترح حل مشكلة باسكارا الهندية القديمة:

"مربع خُمس القرود ، الذي تم تقليصه بمقدار ثلاثة ، مختبئًا في الكهف ، تسلق أحد القرود شجرة ، وكان مرئيًا. كم عدد القرود هناك؟ وتجدر الإشارة إلى أن هذه المشكلة تم حلها أوليًا ، واختزلها إلى معادلة تربيعية.
الخورزمي - عالم عربي كتب كتاب الإصلاح والمعارضة عام 825 م. كان أول كتاب في الجبر في العالم. كما قدم ستة أنواع من المعادلات التربيعية ولكل من المعادلات الست التي صاغها في صيغة لفظية قاعدة خاصة لحلها. في الرسالة ، يسرد خورزمي ستة أنواع من المعادلات ، معبراً عنها على النحو التالي:

1. "المربعات تساوي الجذور" ، أي الفأس 2 = بوصة.

2. "المربعات تساوي العدد" ، أي الفأس 2 = ق.

3. "الجذور تساوي العدد" ، أي آه = ق.

4. "المربعات والأرقام تساوي الجذور" ، أي فأس 2 + ج \ u003d بوصة.

5. "المربعات والجذور تساوي العدد" ، أي الفأس 2 + في = s.

6. "الجذور والأرقام تساوي المربعات" ، أي في + c \ u003d ah 2.

لنحلل مشكلة الخوارزمي التي تختزل في حل معادلة تربيعية. "مربع ورقم يساوي الجذور." على سبيل المثال ، مربع واحد والرقم 21 يساوي 10 جذور لنفس المربع ، أي السؤال هو ، مما يتكون المربع ، والذي بعد إضافة 21 إليه ، يصبح مساويًا لـ 10 جذور لنفس المربع؟

و باستخدام الصيغة الرابعة للخوارزمي ، يجب على الطلاب كتابة: x 2 + 21 = 10x

فرانسوا فيت - عالم رياضيات فرنسي ، صاغ وأثبت النظرية حول مجموع وحاصل جذر المعادلة التربيعية المعطاة.

الفن الذي أقدمه جديدًا ، أو على الأقل تعرض للتلف بسبب تأثير البرابرة الذين رأيته مناسبًا لمنحه مظهرًا جديدًا تمامًا.

فرانسوا فيت

ومع ذلك ، وُلد فرانسوا (1540-13.12. 1603) في بلدة فونتيني لو كومت في مقاطعة بواتو ، بالقرب من قلعة لاروشيل الشهيرة. بعد حصوله على شهادة في القانون ، من سن التاسعة عشرة ، عمل بنجاح كمحام في مسقط رأس. كمحامية ، تمتعت فيت بالاحترام والمكانة بين السكان. كان شخصًا متعلمًا على نطاق واسع. عرف علم الفلك والرياضيات وكل شيء وقت فراغأعطت لهذه العلوم.

العاطفة الرئيسيةكانت فييتا رياضيات. درس بعمق أعمال كلاسيكيات أرخميدس وديوفانتوس ، أسلاف كاردانو وبومبيلي وستيفين وغيرهم. لم يكن فييتا معجبًا بهم فحسب ، بل رأى عيبًا كبيرًا فيها ، وهو صعوبة الفهم بسبب الرمزية اللفظية: تم تسجيل جميع الإجراءات والعلامات تقريبًا بالكلمات ، ولم يكن هناك أي تلميح لتلك القواعد المريحة شبه التلقائية التي نستخدمها الآن . كان من المستحيل التدوين ، وبالتالي البدء في شكل عام ، أو مقارنات جبرية أو أي تعبيرات جبرية أخرى. تم حل كل نوع من المعادلات ذات المعاملات العددية وفقًا لقاعدة خاصة. لذلك ، كان من الضروري إثبات وجود الإجراءات العامةعلى جميع الأرقام التي لا تعتمد على هذه الأرقام نفسها. أثبت فيت وأتباعه أنه لا يهم ما إذا كان الرقم المعني هو عدد الأشياء أو طول المقطع. الشيء الرئيسي هو أنه من الممكن إجراء عمليات جبرية بهذه الأرقام ، ونتيجة لذلك ، مرة أخرى الحصول على أرقام من نفس النوع. ومن ثم يمكن الإشارة إليها ببعض العلامات المجردة. فعل فييت ذلك بالضبط. لم يقدم حساب التفاضل والتكامل الخاص به فحسب ، بل قام باكتشاف جديد جوهريًا ، وحدد لنفسه هدفًا ألا وهو دراسة ليس الأرقام ، بل دراسة الإجراءات عليها. سمحت طريقة التسجيل هذه لـ Vieta بعمل اكتشافات مهمة عند الدراسة الخصائص المشتركةالمعادلات الجبرية. ليس من قبيل المصادفة أن يُطلق على فييتا لقب "أب" الجبر ، مؤسس رموز الحروف.

مصادر المعلومات:

http :// سوم. fio. en/ مصادر/ كاربوهينا/2003/12/ مكتمل%20 الشغل/ حفلة موسيقية/ فهرس1. هتم

http :// الصفحات. مارسو. en/ iac/ المدرسة/ س4/ صفحة74. لغة البرمجة