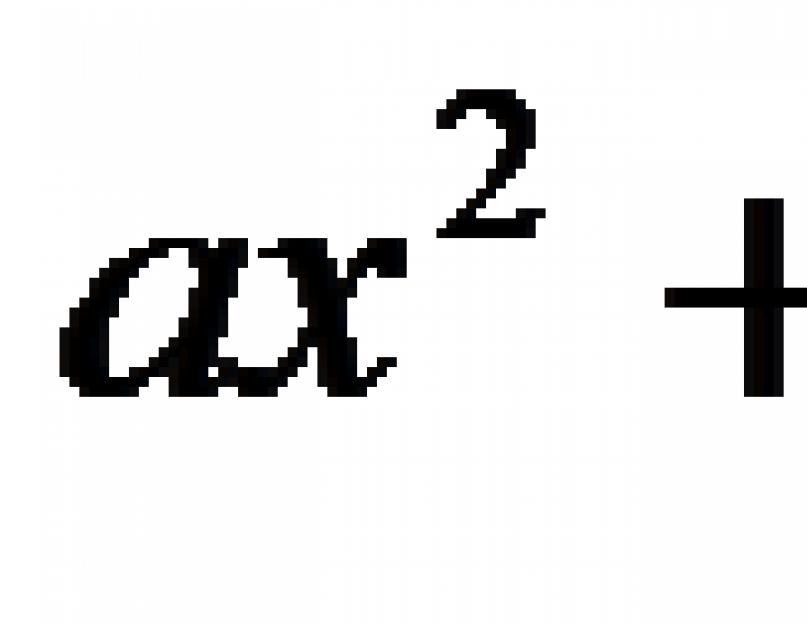Kutatómunka

A témán

"Megoldási módok másodfokú egyenletek »

Teljesített:
csoport 8 "G" osztály

Munkavezető:
Benkovszkaja Mária Mihajlovna

A projekt céljai és célkitűzései.

1. Mutassuk meg, hogy a matematikának, mint minden más tudománynak, elege van a megfejtetlen rejtélyeiből.
2. Hangsúlyozza, hogy a matematikusokat a nem szabványos gondolkodás jellemzi. És néha szellemesség és intuíció jó matematikus egyszerűen csodálatosak!
3. Mutassuk meg, hogy a másodfokú egyenletek megoldására tett kísérlet is hozzájárult új matematikai fogalmak és ötletek kifejlesztéséhez!
4. Tanuljon meg különböző információforrásokkal dolgozni.
5. Folytatás kutatómunka matematika

Kutatási szakaszok

1. A másodfokú egyenletek keletkezésének története.

2. Másodfokú egyenlet definíciója és típusai.

3. Másodfokú egyenletek megoldása a diszkrimináns képlet segítségével.

4. Francois Viet és tétele.

5. Együtthatók tulajdonságai másodfokú egyenlet gyökereinek gyors megtalálásához.

6. Gyakorlati tájékozódás.

Egyenletek, tételek révén

Sok problémát megoldottam.

(Chaucer, angol költő, középkorú.)

színpad. A másodfokú egyenletek kialakulásának története.

Az ókorban nemcsak első, hanem másodfokú egyenletek megoldásának igényét a területkereséssel kapcsolatos problémák megoldásának igénye okozta. földterületekés katonai jellegű földmunkákkal, valamint magával a csillagászat és a matematika fejlődésével.

A babilóniaiak Kr.e. 2000 körül tudtak másodfokú egyenleteket megoldani. A babilóniai szövegekben megfogalmazott ezen egyenletek megoldási szabálya lényegében egybeesik a modernekkel, de nem ismert, hogy a babiloniak hogyan találták meg a szabályt. Az eddig talált ékírásos szövegek szinte mindegyike csak a recept formájában megfogalmazott megoldási problémákat ad, a megtalálás módját nem jelzik.

Ellenére magas szint az algebra fejlődése Babilonban, az ékírásos szövegekben nincs negatív szám fogalma és általános módszerek a másodfokú egyenletek megoldására.

Diophantus "Aritmetikája" szisztematikus feladatsort tartalmaz, magyarázatokkal kísérve és egyenletek megfogalmazásával megoldva. különféle fokozatok, de hiányzik belőle az algebra szisztematikus kifejtése.

A másodfokú egyenletekkel kapcsolatos problémák már megtalálhatók az "Aryabhattiam" csillagászati ​​értekezésekben, amelyeket 499-ben állítottak össze. Aryabhatta indiai matematikus és csillagász. Egy másik indiai tudós, Brahmagupta (7. század) kifejtette Általános szabály másodfokú egyenletek egyetlen kanonikus formára redukált megoldásai:

Al-Khorezmi algebrai értekezése a lineáris és másodfokú egyenletek osztályozását adja meg. A szerzőnek 6 féle egyenlete van. Al-Khwarizminak, aki nem tudta negatív számok, az egyes egyenletek tagjai összeadások, nem pedig részfejek. Ugyanakkor a pozitív megoldásokkal nem rendelkező egyenleteket szándékosan nem veszik figyelembe; egy hiányos másodfokú egyenlet megoldása során al-Khwarizmi, mint minden 17. század előtti tudós, nem veszi figyelembe a nulla megoldást.

Al-Khwarizmi értekezése az első olyan könyv, amely eljutott hozzánk, amelyben szisztematikusan bemutatják a másodfokú egyenletek osztályozását és a megoldási képleteket.

A másodfokú egyenletek al-Khwarizmi mintájára Európában történő megoldására szolgáló képleteket először az Abakusz könyve adta meg, amelyet Leonardo Fibonacci olasz matematikus írt 1202-ben. Ezt a terjedelmes művet a teljesség és a bemutatás egyértelműsége jellemzi. A szerző önállóan dolgozott ki néhány új algebrai feladatmegoldási módszert, és Európában elsőként közelítette meg a negatív számok bevezetését. Könyve hozzájárult az algebrai ismeretek elterjedéséhez nemcsak Olaszországban, hanem Németországban, Franciaországban és más európai országokban is. Az Abakusz könyvéből sok probléma bekerült szinte az összes 16-17. és részben 18. századi európai tankönyvbe.

Általános szabály a másodfokú egyenletek megoldására egyetlen kanonikus alakra redukálva minden lehetséges jelkombinációval együtthatók b,c Európában csak 1544-ben fogalmazta meg M. Stiefel.

Másodfokú egyenlet megoldási képletének levezetése in Általános nézet Vietnek vannak, de Viet csak pozitív gyökereket ismert fel. Tartaglia, Cardano, Bombelli olasz matematikusok a 16. században az elsők között vették figyelembe nemcsak a pozitív, hanem a negatív gyökereket is. Csak a 17. században, Girrard, Descartes, Newton és más tudósok munkáinak köszönhetően, a másodfokú egyenletek megoldásának módszere öltött modern formát.

KIDERÜL:

A másodfokú egyenletekkel kapcsolatos problémák már 499-ben találhatók.

NÁL NÉL ősi india nyilvános versenyeket rendeztek nehéz feladatok megoldásában - OLIMPIÁDOK .

©2015-2019 oldal
Minden jog a szerzőket illeti. Ez az oldal nem igényel szerzői jogot, de ingyenesen használható.
Az oldal létrehozásának dátuma: 2016-04-11

Különböző civilizációk képviselői: Az ókori Egyiptom, ókori Babilon, Ókori Görögország, ókori India, Ősi Kína, Középkori Kelet, Európa elsajátította a másodfokú egyenletek megoldásának technikáit.

Az ókori Egyiptom matematikusai először tudtak másodfokú egyenletet megoldani. Az egyik matematikai papirusz a következő problémát tartalmazza:

"Keresse meg egy téglalap alakú mező oldalait, ha területe 12, és - a hossza megegyezik a szélességével." „A mező hossza 4” – mondja a papirusz.

Évezredek teltek el, negatív számok léptek be az algebrába. Az x² = 16 egyenletet megoldva két számot kapunk: 4, -4.

Természetesen az egyiptomi feladatban X = 4-et vennénk, mivel a mező hossza csak pozitív érték lehet.

A hozzánk eljutott források azt mutatják, hogy az ókori tudósok rendelkeztek néhány általános módszerrel az ismeretlen mennyiségekkel kapcsolatos problémák megoldására. A másodfokú egyenletek megoldásának szabálya, amelyet a babiloni szövegek lefektetnek, lényegében megegyezik a modernnel, de nem ismert, hogy a babilóniaiak hogyan „jutottak idáig”. De szinte minden megtalálható papiruszban és ékírásos szövegben csak a megoldással kapcsolatos problémák szerepelnek. A szerzők csak néha mellékelték numerikus számításaikat olyan átlagos megjegyzésekkel, mint: „Nézd!”, „Csináld!”, „Jól találtad!”.

Diophantus görög matematikus másodfokú egyenleteket írt és oldott meg. "Aritmetikája" nem tartalmazza az algebra szisztematikus bemutatását, de szisztematikus feladatsort tartalmaz, magyarázatokkal kísérve, és különböző fokú egyenletek összeállításával megoldva.

A másodfokú egyenletek összeállítására vonatkozó feladatok már megtalálhatók az "Aria-bhatiam" csillagászati ​​értekezésben, amelyet Ariabhatta indiai matematikus és csillagász állított össze 499-ben.

Egy másik indiai tudós, Brahmagupta (7. század) felvázolta az ax² + bx = c alakú másodfokú egyenletek megoldásának általános szabályát.

Az ókori Indiában gyakoriak voltak a nyilvános versenyek a nehéz problémák megoldásában. Az egyik régi indiai könyv az ilyen versenyekről a következőt mondja: „Ahogy a nap ragyogásával felülmúlja a csillagokat, úgy tudós ember elhomályosítani egy másik dicsőségét nyilvános üléseken, algebrai problémákat javasolva és megoldva. A feladatokat gyakran költői formába öltöztették.

Itt van a XII. század híres indiai matematikusának egyik problémája. Bhaskara:

Nyüzsgő majmok csapata

Jól étkezni, szórakozni.

Nyolcadik részük a téren a tisztáson mulatott.

És tizenketten a szőlő mellett… ugrálni kezdtek, lógva…​

Hány majom volt

Mondja, ebben a nyájban?

Bhaskara megoldása azt jelzi, hogy tudott a másodfokú egyenletek gyökereinek kétértékűségéről.

A legősibb kínai matematikai szövegek, amelyek hozzánk jutottak, a Kr.e. I. század végére nyúlnak vissza. IDŐSZÁMÍTÁSUNK ELŐTT. A II században. IDŐSZÁMÍTÁSUNK ELŐTT. Matematika Kilenc könyvben íródott. Később, a 7. században bekerült a "Tíz klasszikus traktátus" gyűjteményébe, amelyet évszázadokon át tanulmányoztak. A „Matematika kilenc könyvben” című értekezés elmagyarázza, hogyan lehet kivonni a négyzetgyököt a két szám összegének négyzetének képletével.

A módszert "tian-yuan"-nak (szó szerint - "mennyei elemnek") hívták - mivel a kínaiak egy ismeretlen mennyiséget jelöltek.​

Az első, széles körben ismertté vált problémamegoldó útmutató a 9. századi bagdadi tudós munkája volt. Mohamed bin Musza al-Khwarizmi. Az "al-jabr" szó - idővel a jól ismert "algebra" szóvá változott, és maga az al-Khwarizmi összetétele is Kiindulópont az egyenletmegoldás tudományának fejlődésében. Al-Khorezmi algebrai értekezése a lineáris és másodfokú egyenletek osztályozását adja meg. A szerző hatféle egyenletet sorol fel, ezeket a következőképpen fejezi ki:

-négyzetek egyenlő gyökök, vagyis ah ² = bx;

-egyenlő számú négyzet, vagyis ah ² = c;

-a gyökök egyenlőek a számmal, azaz ax = c;

-a négyzetek és a számok egyenlőek a gyökökkel, vagyis ah ²+ c \u003d bx;

-négyzetek és gyökök egyenlőek a számmal, vagyis ah ² + bx \u003d c;

-a gyökök és a számok négyzetek, azaz bx + c = ax ²;

Al-Khwarizmi értekezése az első olyan könyv, amely eljutott hozzánk, amelyben szisztematikusan bemutatják a másodfokú egyenletek osztályozását, és megadják a megoldásukra vonatkozó képleteket.

A másodfokú egyenletek al-Khwarizmi mintájára Európában történő megoldására szolgáló képleteket először az Abakusz könyve adta meg, amelyet Leonardo Fibonacci olasz matematikus írt 1202-ben. A szerző önállóan dolgozott ki néhány új algebrai problémamegoldási példát, és Európában elsőként közelítette meg a negatív számok bevezetését. Könyve hozzájárult az algebrai ismeretek elterjedéséhez nemcsak Olaszországban, hanem Németországban, Franciaországban és más európai országokban is. Az Abakusz könyvéből sok feladat bekerült szinte minden 16-17. századi európai tankönyvbe. és a 18. század egy része.

A másodfokú egyenletek megoldásának általános szabálya egyetlen x kanonikus alakra redukálva ² + bx \u003d c, a b és c együtthatók minden lehetséges előjelének kombinációjával, Európában csak 1544-ben fogalmazta meg M. Stiefel.

Vietának van egy általános levezetése a másodfokú egyenlet megoldására, de ő is csak pozitív gyököket ismert fel. Tartaglia, Cardano, Bombelli olasz matematikusok az elsők között voltak a 16. században. a pozitív és negatív gyökerek mellett vegye figyelembe. Csak a 17. században, Girard, Descartes, Newton és más tudósok munkáinak köszönhetően, a másodfokú egyenletek megoldásának módszere öltött modern formát.

​

​

Kopjevszkaja vidéki középiskola

10 módszer a másodfokú egyenletek megoldására

Vezető: Patrikeeva Galina Anatoljevna,

matematika tanár

s.Kopyevo, 2007

1. A másodfokú egyenletek kialakulásának története

1.1 Másodfokú egyenletek az ókori Babilonban

1.2 Hogyan állította össze és oldotta meg Diophantus a másodfokú egyenleteket

1.3 Másodfokú egyenletek Indiában

1.4 Másodfokú egyenletek al-Khwarizmiban

1.5 Másodfokú egyenletek Európában XIII - XVII. század

1.6 Vieta tételéről

2. Másodfokú egyenletek megoldási módszerei

Következtetés

Irodalom

1. A másodfokú egyenletek kialakulásának története

1.1 Másodfokú egyenletek az ókori Babilonban

Az ókorban nemcsak az első, hanem a másodfokú egyenletek megoldásának igényét a katonai jellegű földterületek és földművek felkutatásával, valamint a csillagászat fejlődésével kapcsolatos problémák megoldásának igénye okozta. maga a matematika. A másodfokú egyenleteket Kr.e. 2000 körül tudták megoldani. e. babilóniaiak.

A modern algebrai jelölést alkalmazva elmondhatjuk, hogy ékírásos szövegeikben a hiányos szövegeken kívül vannak például teljes másodfokú egyenletek:

x 2 + x = ¾; x 2 - x = 14,5

Az egyenletek megoldására vonatkozó, a babiloni szövegekben megfogalmazott szabály lényegében egybeesik a modernnel, de nem ismert, hogy a babilóniaiak hogyan jutottak el ehhez a szabályhoz. Az eddig talált ékírásos szövegek szinte mindegyike csak a recept formájában megfogalmazott megoldási problémákat ad, a megtalálás módját nem jelzik.

Annak ellenére, hogy Babilonban magas az algebra fejlettsége, az ékírásos szövegekből hiányzik a negatív szám fogalma és a másodfokú egyenletek megoldásának általános módszerei.

1.2 Hogyan állította össze és oldotta meg Diophantus a másodfokú egyenleteket.

Diophantus aritmetikája nem tartalmazza az algebra szisztematikus kifejtését, hanem egy szisztematikus feladatsort tartalmaz magyarázatokkal kísérve, amelyeket különböző fokú egyenletek felállításával oldanak meg.

Az egyenletek összeállításakor Diophantus ügyesen választ ismeretleneket, hogy leegyszerűsítse a megoldást.

Itt van például az egyik feladata.

11. feladat."Keress két számot úgy, hogy az összegük 20, a szorzatuk pedig 96"

Diophantus a következőképpen érvel: a feladat feltételéből az következik, hogy a kívánt számok nem egyenlőek, hiszen ha egyenlőek lennének, akkor a szorzatuk nem 96 lenne, hanem 100. Így az egyik a számuk több mint fele lesz. összeg, azaz . 10+x, a másik kisebb, i.e. 10-es. A különbség köztük 2x .

Ezért az egyenlet:

(10 + x) (10 - x) = 96

100 - x 2 = 96

x 2-4 = 0 (1)

Innen x = 2. A kívánt számok egyike 12 , Egyéb 8 . Megoldás x = -2 mert Diophantus nem létezik, mivel a görög matematika csak pozitív számokat ismert.

Ha ezt a feladatot úgy oldjuk meg, hogy a kívánt számok egyikét ismeretlennek választjuk, akkor eljutunk az egyenlet megoldásához

y(20 - y) = 96,

y 2 - 20y + 96 = 0. (2)

Nyilvánvaló, hogy Diophantus leegyszerűsíti a megoldást azzal, hogy a kívánt számok félkülönbségét választja ismeretlennek; sikerül a problémát egy hiányos másodfokú egyenlet (1) megoldására redukálnia.

1.3 Másodfokú egyenletek Indiában

A másodfokú egyenletekkel kapcsolatos problémák már megtalálhatók az "Aryabhattam" csillagászati ​​traktátusban, amelyet Aryabhatta indiai matematikus és csillagász állított össze 499-ben. Egy másik indiai tudós, Brahmagupta (7. század) felvázolta az egyetlen kanonikus formára redukált másodfokú egyenletek megoldásának általános szabályát:

ah 2+ b x = c, a > 0. (1)

Az (1) egyenletben az együtthatók, kivéve a a, negatív is lehet. Brahmagupta uralma lényegében egybeesik a miénkkel.

Az ókori Indiában gyakoriak voltak a nyilvános versenyek a nehéz problémák megoldásában. Az egyik régi indiai könyvben a következőt mondják az ilyen versenyekről: „Ahogy a nap felülmúlja a csillagokat ragyogásával, úgy a tanult ember is felülmúlja a másik dicsőségét a nyilvános összejöveteleken, algebrai feladatokat javasolva és megoldva.” A feladatokat gyakran költői formába öltöztették.

Itt van a XII. század híres indiai matematikusának egyik problémája. Bhaskara.

13. feladat.

„Egy nyüzsgő majomcsapat és tizenkettő a szőlőben…

Miután evett erőt, jól érezte magát. Ugrálni kezdtek, lógva...

Nyolcadik részük egy négyzetben Hány majom volt ott,

Szórakozás a réten. Mondja, ebben a nyájban?

Bhaskara megoldása azt jelzi, hogy tudott a másodfokú egyenletek gyökeinek kétértékűségéről (3. ábra).

A 13. feladatnak megfelelő egyenlet:

( x /8) 2 + 12 = x

Bhaskara ezt írja leple alatt:

x 2 - 64x = -768

és kiegészíteni bal oldal ennek az egyenletnek a négyzetéhez, mindkét oldalhoz hozzáadódik 32 2 , akkor kapok:

x 2 - 64x + 32 2 = -768 + 1024,

(x - 32) 2 = 256,

x - 32 = ± 16,

x 1 = 16, x 2 = 48.

1.4 Másodfokú egyenletek al-Khorezmiben

Al-Khorezmi algebrai értekezése a lineáris és másodfokú egyenletek osztályozását adja meg. A szerző 6 típusú egyenletet sorol fel, ezeket a következőképpen fejezi ki:

1) "A négyzetek egyenlőek a gyökökkel", azaz. ax 2 + c = b X.

2) "A négyzetek egyenlőek a számmal", azaz. ax 2 = s.

3) "A gyökök egyenlőek a számmal", azaz. ah = s.

4) "A négyzetek és a számok egyenlőek a gyökkel", azaz. ax 2 + c = b X.

5) "A négyzetek és a gyökök egyenlőek a számmal", azaz. ah 2+ bx = s.

6) "A gyökök és a számok egyenlőek a négyzetekkel", azaz. bx + c \u003d ax 2.

Al-Khwarizmi számára, aki kerülte a negatív számok használatát, ezen egyenletek mindegyike összeadás, nem kivonás. Ebben az esetben nyilvánvalóan nem veszik figyelembe azokat az egyenleteket, amelyeknek nincs pozitív megoldása. A szerző felvázolja ezen egyenletek megoldásának módszereit al-jabr és al-muqabala módszereivel. Döntései természetesen nem teljesen esnek egybe a miénkkel. Arról nem is beszélve, hogy pusztán retorikai, meg kell jegyezni például, hogy az első típusú hiányos másodfokú egyenlet megoldásakor

al-Khorezmi, mint minden matematikus a 17. század előtt, nem veszi figyelembe a nulla megoldást, valószínűleg azért, mert az konkrét gyakorlati problémáknál nem számít. A teljes másodfokú egyenletek megoldása során al-Khorezmi meghatározott numerikus példák segítségével meghatározza a megoldási szabályokat, majd a geometriai bizonyításokat.

14. feladat.„A négyzet és a 21-es szám egyenlő 10 gyökkel. Találd meg a gyökeret" (az x 2 + 21 = 10x egyenlet gyökerét feltételezve).

A szerző megoldása valahogy így hangzik: oszd el a gyökök számát felére, kapsz 5-öt, 5-öt megszorozod önmagával, a szorzatból kivonod a 21-et, marad 4. Vedd a 4 gyökét, kapsz 2-t. Vonsz ki 2-t 5-ből, kap 3-at, ez lesz a kívánt gyökér. Vagy adj hozzá 2-t az 5-höz, ami 7-et ad, ez is egy gyökér.

A Treatise al - Khorezmi az első olyan könyv, amely eljutott hozzánk, amelyben szisztematikusan leírják a másodfokú egyenletek osztályozását, és megadják a megoldásukra vonatkozó képleteket.

1.5 Másodfokú egyenletek Európában XIII - A XVII században

A másodfokú egyenletek megoldásának képleteit az al-Khorezmi mintájára Európában először az "Abakusz könyve" írta le, amelyet 1202-ben Leonardo Fibonacci olasz matematikus írt. Ez a terjedelmes munka, amely a matematika hatását tükrözi mind az iszlám országaiban, mind az ókori Görögországban, mind a teljesség, mind az áttekinthetőség jellemzi. A szerző önállóan dolgozott ki néhány új algebrai problémamegoldási példát, és Európában elsőként közelítette meg a negatív számok bevezetését. Könyve hozzájárult az algebrai ismeretek elterjedéséhez nemcsak Olaszországban, hanem Németországban, Franciaországban és más európai országokban is. Az „Abakusz könyvéből” sok feladat bekerült szinte az összes 16-17. századi európai tankönyvbe. részben pedig XVIII.

A másodfokú egyenletek megoldásának általános szabálya egyetlen kanonikus formára redukálva:

x 2+ bx = vele,

az együtthatók minden lehetséges előjel-kombinációjára b , Val vel Európában csak 1544-ben fogalmazta meg M. Stiefel.

Vietának van egy általános levezetése a másodfokú egyenlet megoldására, de Vieta csak pozitív gyököket ismert fel. Tartaglia, Cardano, Bombelli olasz matematikusok az elsők között voltak a 16. században. A pozitív és negatív gyökerek mellett vegye figyelembe. Csak a XVII. Köszönhetően Girard, Descartes, Newton és mások munkájának tudósok módjára a másodfokú egyenletek megoldása modern formát ölt.

1.6 Vieta tételéről

A Vieta nevet viselő másodfokú egyenlet együtthatói és gyökei közötti összefüggést kifejező tételt először 1591-ben fogalmazta meg így: „Ha B + D szorozva A - A 2 , egyenlő BD, akkor A egyenlő NÁL NÉLés egyenlő D ».

Ahhoz, hogy megértsük Vietát, emlékeznünk kell erre DE, mint minden magánhangzó, számára az ismeretlent jelentette (a mi x), a magánhangzók NÁL NÉL, D- együtthatók az ismeretlenre. A modern algebra nyelvén Vieta fenti megfogalmazása azt jelenti: ha

(egy + b )x - x 2 = ab ,

x 2 - (a + b )x + a b = 0,

x 1 = a, x 2 = b .

Az egyenletek gyökei és együtthatói közötti kapcsolatot szimbólumokkal írt általános képletekkel kifejezve, Viet egységességet állapított meg az egyenletek megoldási módszereiben. Vieta szimbolikája azonban még messze van modern megjelenés. Nem ismerte fel a negatív számokat, ezért az egyenletek megoldása során csak azokat az eseteket vette figyelembe, ahol minden gyök pozitív.

2. Másodfokú egyenletek megoldási módszerei

A másodfokú egyenletek képezik az alapot, amelyre a fenséges épület algebra. Másodfokú egyenletek találni széles körű alkalmazás trigonometrikus, exponenciális, logaritmikus, irracionális és transzcendentális egyenletek és egyenlőtlenségek megoldása során. Mindannyian tudjuk, hogyan kell másodfokú egyenleteket megoldani az iskolától (8. osztály) egészen az érettségiig.

Kezdőlap > Jelentés

Hősökről elnevezett MOU középiskola szovjet Únió
Sotnikova A.T. és Shepeleva N. G. s. Uritskoe

Beszámoló a témáról:

"A megjelenés története

másodfokú egyenletek"

Készítette:Izotova Julia,
Ampleeva Elena,
Nyikolaj Sepelev,

Djacsenko Jurij.

Ó, matematika. Évszázadokon át borít a dicsőség,

Minden földi világítótest lámpása.

Te fenséges királynő

Nem csoda, hogy Gauss megkeresztelkedett.

Szigorú, logikus, fenséges,

Repülés közben karcsú, mint egy nyíl,

Örök dicsőséged

Az idők során halhatatlanságra tett szert.

Dicsérjük az emberi elmét

a tetteit varázslatos kezek,

E kor reménysége

Minden földi tudomány királynője.

Ma szeretnénk elmondani

Előfordulás története

Amit minden diáknak tudnia kell

A másodfokú egyenletek története.

Eukleidész, a Kr.e. III. században. e. a geometriai algebrának szentelt "Elvek"-ben a teljes második könyvet, amely minden szükséges anyagot tartalmaz a másodfokú egyenletek megoldásához.

Euklidész (Eνκλειδηζ), ókori görög matematikus, az első hozzánk eljutott matematikai elméleti értekezés szerzője

Euklidészről rendkívül kevés információ áll rendelkezésre. Az egyetlen dolog, ami megbízhatónak tekinthető, az tudományos tevékenység az ie III. században Alexandriában folyt. e. Eukleidész az alexandriai iskola első matematikusa. Övé fő munka A "Kezdetek" (latinizált formában - "Elemek") a planimetria, a sztereometria és számos számelméleti kérdés bemutatását tartalmazza; benne foglalta össze a görög matematika korábbi fejlődését és megteremtette az alapot további fejlődés matematika. Gém - Görög matematikus és mérnök először Görögországban a Kr.u. I. században. tisztán algebrai módszert ad a másodfokú egyenlet megoldására.

Alexandriai gém; Gém, én c. n. e., görög mechanikus és matematikus. Életének ideje bizonytalan, csak annyit tudni, hogy Arkhimédészt (aki Kr. e. 212-ben halt meg), őt magát Pappus (i.sz. 300 körül) idézte. Jelenleg az a vélemény uralkodik, hogy az I. században élt. n. e. Geometriát, mechanikát, hidrosztatikát, optikát tanult; feltalálta a gőzgép prototípusát és a precíziós szintező műszereket. A legnépszerűbb automaták az automata színházak, szökőkutak és egyebek voltak.G. a statika és a kinetika törvényeire támaszkodva leírta a teodolitot, leírást adott a karról, a blokkról, a propellerről és a katonai járművekről. Az optikában a fényvisszaverődés törvényeit fogalmazta meg, a matematikában - a legfontosabb mérési módszereket. geometriai formák. G. fő művei az Etrika, Pneumatika, Autopoietika, Mechanika (francia; a mű teljes egészében arabul őrződött meg), a Katoptika (a tükrök tudománya; csak Latin fordítás) és mások.. G. felhasználta elődei vívmányait: Euklidész, Arkhimédész, Lampsakból származó Strato. Stílusa egyszerű és világos, bár néha túl lakonikus vagy strukturálatlan. G. írásai iránti érdeklődés a III. n. e. Görög, majd bizánci és arab diákok kommentálták és fordították műveit.

Diophantus- egy görög tudós a Kr.u. 3. században, anélkül, hogy a geometriához folyamodott volna, néhány másodfokú egyenletet tisztán algebrai módon oldott meg, és magát az egyenletet és megoldását szimbolikus formában írták le.

„Elmondom, hogyan alkotott és oldott meg másodfokú egyenleteket a görög matematikus, Diophantus. Itt van például az egyik feladata:"Keress két számot úgy, hogy az összegük 20, a szorzatuk pedig 96."

1. A feladat feltételéből következik, hogy a kívánt számok nem egyenlőek, mert ha egyenlőek lennének, akkor a szorzatuk nem 96, hanem 100 lenne.

2. Így. egyikük több mint a fele lesz az összegüknek, i.e. 10 + x, a másik kisebb, azaz. 10 - x.

3. A különbség köztük 2x.

4. Ebből adódik a (10 + x) * (10 - x) = 96 egyenlet

100 - x 2 = 96 x 2 - 4 = 0

5. Válasz x = 2. A kívánt számok egyike a 12,
egyéb - 8. Az x = - 2 megoldás Diophantus esetében nem létezik, mert A görög matematika csak pozitív számokat ismert. Diophantus tudta, hogyan kell megoldani nagyon összetett egyenleteket, amelyeket ismeretlenekre használtak betűjelölések, bevezetett egy speciális szimbólumot a számításhoz, szórövidítéseket használt. Bhaskare – Akaria- Indiai matematikus a XII. században. nyitott általános módszer másodfokú egyenletek megoldásai.

Elemezzük az indiai matematikusok egyik problémáját, például Bhaskara problémáját:

„Egy nyáj majom szórakozik: nyolcaduk egy négyzeten tréfálkodik az erdőben, a maradék tizenkettő a halom tetején sikít. Mondd, hány majom van?

A feladatot kommentálva azt szeretném mondani, hogy az (x/8) 2 + 12 = x egyenlet felel meg a feladatnak. Bhaskara x 2 - 64x \u003d - 768 alakot ír. Ha mindkét részhez hozzáadjuk a 32-es négyzetet, az egyenlet a következőképpen alakul:

x 2 - 64 x + 32 2 = - 768 + 1024

(x - 32) 2 = 256

A négyzetgyök kinyerése után a következőt kapjuk: x - 32 = 16.

"NÁL NÉL ez az eset, mondja Bhaskara, - az első rész negatív egységei olyanok, hogy a második rész egységei kisebbek náluk, és ezért az utóbbit tekinthetjük pozitívnak és negatívnak is, és megkapjuk az ismeretlen kettős értékét: 48 ill. 16.

Meg kell állapítani, hogy Bhaskara megoldása azt jelzi, hogy tudott a másodfokú egyenletek gyökereinek kétértékűségéről.

A régi indiai Bhaskara probléma megoldását javasolják:

„A majmok egyötödének négyzete hárommal csökkentve megbújt a barlangban, egy majom felmászott egy fára, látszott. Hány majom volt? Meg kell jegyezni, hogy ez a probléma elemileg megoldott, másodfokú egyenletre redukálva.
Al - Khorezmi - egy arab tudós, aki 825-ben megírta a "A helyreállítás és az ellenállás könyve" című könyvet. Ez volt a világ első algebrai tankönyve. Hatféle másodfokú egyenletet is adott, és mind a hat egyenletre, amelyeket verbális formában fogalmazott meg, egy speciális szabályt ennek megoldására. A dolgozatban Khorezmi 6 típusú egyenletet sorol fel, ezeket a következőképpen fejezi ki:

1. "A négyzetek egyenlőek a gyökökkel", azaz. ax 2 = in.

2. "A négyzetek egyenlőek a számmal", azaz. ax 2 = s.

3. "A gyökök egyenlőek a számmal", azaz. ah = s.

4. "A négyzetek és a számok egyenlőek a gyökekkel", azaz. ax 2 + c \u003d be.

5. "A négyzetek és a gyökök egyenlőek a számmal", azaz. ax 2 + in = s.

6. "A gyökök és a számok egyenlőek a négyzetekkel", azaz. in + c \u003d ah 2.

Elemezzük al-Khwarizmi problémáját, amely egy másodfokú egyenlet megoldására redukálódik. "Egy négyzet és egy szám egyenlő a gyökekkel." Például egy négyzet és a 21-es szám egyenlő ugyanannak a négyzetnek 10 gyökével, azaz. a kérdés az, hogy miből alakul ki egy négyzet, amelyhez 21-et hozzáadva egyenlő lesz ugyanannak a négyzetnek a 10 gyökével?

És al-Khwarizmi 4. képletével a tanulóknak fel kell írniuk: x 2 + 21 = 10x

François Viet - francia matematikus, megfogalmazta és bebizonyította az adott másodfokú egyenlet gyökeinek összegére és szorzatára vonatkozó tételt.

Az általam bemutatott művészet új, vagy legalábbis annyira elrontotta a barbárok hatása, hogy jónak láttam teljesen új külsőt adni.

François Viet

Pedig François (1540-13.12.1603) Fontenay-le-Comte városában született Poitou tartományban, nem messze a híres La Rochelle erődtől. Jogi diploma megszerzése után tizenkilenc éves korától sikeresen praktizált ügyvédként szülőváros. Ügyvédként Viet tekintélyt és tiszteletet élvezett a lakosság körében. Széleskörűen művelt ember volt. Ismerte a csillagászatot, a matematikát és minden mást Szabadidő adott ezeknek a tudományoknak.

Fő szenvedély Vieta matematika volt. Mélyen tanulmányozta Arkhimédész és Diophantus klasszikusok műveit, Cardano, Bombelli, Stevin és mások közvetlen elődjeit. Vieta nemcsak csodálta őket, hanem egy nagy hibát is látott bennük, ami a verbális szimbolikából adódó megértés nehézsége volt: Szinte minden cselekvést és jelet szavakkal rögzítettek, nyoma sem volt azoknak a kényelmes, szinte automatikus szabályoknak, amelyeket most használunk. . Lehetetlen volt leírni, és ezért általános formában elkezdeni algebrai összehasonlításokat vagy bármilyen más algebrai kifejezést. Minden numerikus együtthatós egyenlettípust egy speciális szabály szerint oldottak meg. Ezért be kellett bizonyítani, hogy vannak általános akciók minden olyan számon, amely nem függ ezektől a számoktól. Viet és követői megállapították, hogy nem mindegy, hogy a szóban forgó szám az objektumok száma vagy a szakasz hossza. A lényeg az, hogy ezekkel a számokkal lehetséges algebrai műveleteket végrehajtani, és ennek eredményeként ismét azonos típusú számokat kapni. Ezért néhány absztrakt jellel jelölhetők. Viet pont ezt tette. Nemcsak bevezette a szó szerinti számítását, hanem egy alapvetően új felfedezést tett, és azt a célt tűzte ki maga elé, hogy ne a számokat, hanem az azokon végzett cselekvéseket tanulmányozza. Ez a felvételi módszer lehetővé tette Vietának, hogy fontos felfedezéseket tegyen tanulmányai során közös tulajdonságok algebrai egyenletek. Nem véletlenül nevezik Vietát az algebra "atyjának", a betűszimbólumok megalapítójának.

Információs források:

http :// som. fio. hu/ erőforrások/ Karpuhina/2003/12/ Befejezve%20 munka/ Koncert/ index1. htm

http :// oldalakat. marsu. hu/ iac/ iskola/ s4/ oldalon74. html