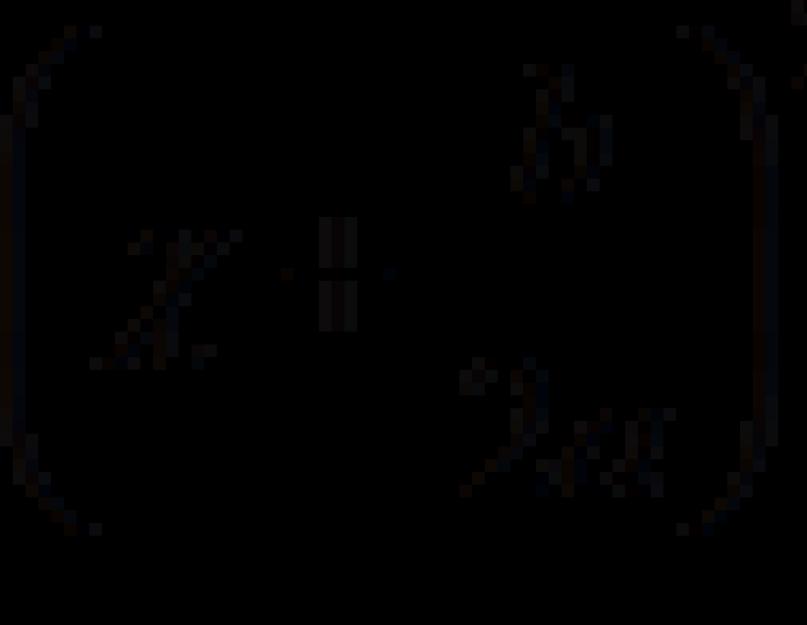Az előfordulás történetéből másodfokú egyenletek

Az algebra különféle problémák egyenletekkel történő megoldása kapcsán merült fel. Általában problémák esetén egy vagy több ismeretlent kell találni, miközben ismerjük a kívánt és megadott mennyiségeken végrehajtott egyes műveletek eredményét. Az ilyen feladatok egy vagy több egyenletrendszer megoldására redukálódnak, adott mennyiségeken végzett algebrai műveletek segítségével a kívántak megtalálására. Algebra tanulmányok általános tulajdonságok mennyiségekkel kapcsolatos intézkedések.

A lineáris és másodfokú egyenletek megoldására szolgáló algebrai módszerek már 4000 évvel ezelőtt ismertek voltak. Ókori Babilon.

Másodfokú egyenletek az ókori Babilonban

Az ókorban nemcsak az első, hanem a másodfokú egyenletek megoldásának igényét a katonai jellegű földterületek és földművek felkutatásával, valamint a csillagászat fejlődésével kapcsolatos problémák megoldásának igénye okozta. maga a matematika. A babilóniaiak Kr.e. 2000 körül tudták, hogyan kell másodfokú egyenleteket megoldani. A modern algebrai jelölést alkalmazva elmondhatjuk, hogy ékírásos szövegeikben a hiányos szövegeken kívül vannak például teljes másodfokú egyenletek:

https://pandia.ru/text/78/002/images/image002_15.gif" width="93" height="41 src=">

Az egyenletek megoldására vonatkozó, a babiloni szövegekben megfogalmazott szabály lényegében egybeesik a modernnel, de nem ismert, hogy a babilóniaiak hogyan jutottak el ehhez a szabályhoz. Az eddig talált ékírásos szövegek szinte mindegyike csak a recept formájában megfogalmazott megoldási problémákat ad, a megtalálás módját nem jelzik. Annak ellenére magas szint Az algebra fejlődése Babilonban, az ékírásos szövegekből hiányzik a koncepció negatív számÉs közös módszerek másodfokú egyenletek megoldásai.

Diophantus aritmetikája nem tartalmazza az algebra szisztematikus kifejtését, hanem egy szisztematikus feladatsort tartalmaz magyarázatokkal kísérve, amelyeket különböző fokú egyenletek felállításával oldanak meg.

Az egyenletek összeállításakor Diophantus ügyesen választ ismeretleneket, hogy leegyszerűsítse a megoldást.

Itt van például az egyik feladata.

2. feladat "Keress két számot, tudva, hogy összegük 20, szorzatuk pedig 96."

Diophantus a következőképpen érvel: a feladat feltételéből az következik, hogy a kívánt számok nem egyenlőek, hiszen ha egyenlőek lennének, akkor a szorzatuk nem 96, hanem 100 lenne. Így az egyik több lesz, mint összegük fele, azaz .10 + x. A másik kisebb, azaz 10 - x. 2x a különbség köztük. Ezért az egyenlet:

(10+x)(10-x)=96,

Tehát x = 2. A kívánt számok egyike 12, a másik 8. Az x = - 2 megoldás Diophantusra nem létezik, mivel a görög matematika csak pozitív számokat ismert.

Ha ezt a feladatot megoldjuk, az egyik ismeretlen számot ismeretlennek választva, akkor eljuthatunk az egyenlet megoldásához:

Nyilvánvaló, hogy Diophantus leegyszerűsíti a megoldást azzal, hogy a kívánt számok félkülönbségét választja ismeretlennek; sikerül a problémát egy hiányos másodfokú egyenlet megoldására redukálnia.

Másodfokú egyenletek Indiában

A másodfokú egyenletekkel kapcsolatos problémák már megtalálhatók az Aryabhattam csillagászati értekezésben, amelyet Aryabhatta indiai matematikus és csillagász állított össze 499-ben. Egy másik indiai tudós, Brahmagupta (7. század) kifejtette Általános szabály másodfokú egyenletek egyetlen kanonikus formára redukált megoldásai:

ax2 + bx = c, a>

Az (1) egyenletben az együtthatók negatívak is lehetnek. Brahmagupta uralma lényegében egybeesik a miénkkel.

Indiában gyakoriak voltak a nyilvános versenyek a nehéz problémák megoldásában. Az egyik régi indiai könyvben a következőt mondják az ilyen versenyekről: „Ahogy a nap ragyogásával felülmúlja a csillagokat, úgy tudós ember eclipse dicsőség a népszerű összeállításokban, algebrai problémákat kínálva és megoldva. A feladatokat gyakran költői formába öltöztették.

Itt van a XII. század híres indiai matematikusának egyik problémája. Bhaskara.

Bhaskara megoldása azt jelzi, hogy a szerző tisztában volt a másodfokú egyenletek gyökereinek kétértékűségével.

A 3. feladatnak megfelelő egyenlet:

https://pandia.ru/text/78/002/images/image004_11.gif" width="12" height="26 src=">x2 - 64x = - 768

és kiegészíteni bal oldal ennek az egyenletnek a négyzetéig, mindkét oldalához hozzáad 322-t, majd kap:

x2 - b4x + 322 = -768 + 1024,

(x - 32) 2 = 256,

x1 = 16, x2 = 48.

Al-Khwarizmi másodfokú egyenletei

Al-Khwarizmi algebrai értekezése a lineáris és másodfokú egyenletek osztályozását adja meg. A szerző 6 típusú egyenletet sorol fel, ezeket a következőképpen fejezi ki:

1) „A négyzetek egyenlőek a gyökekkel”, azaz ax2 = bx.

2) „A négyzetek egyenlőek a számmal”, azaz ax2 = c.

3) "A gyökerek egyenlőek a számmal", azaz ax \u003d c.

4) „A négyzetek és a számok egyenlőek a gyökekkel”, azaz ax2 + c = bx.

5) „A négyzetek és a gyökök egyenlőek a számmal”, azaz ax2 + bx = c.

6) „A gyökök és a számok egyenlőek a négyzetekkel”, azaz bx + c == ax2.

Al-Khwarizmi számára, aki kerülte a negatív számok használatát, ezen egyenletek mindegyike összeadás, nem kivonás. Ebben az esetben nyilvánvalóan nem veszik figyelembe azokat az egyenleteket, amelyeknek nincs pozitív megoldása. A szerző felvázolja ezen egyenletek megoldásának módszereit al-jabr és al-muqabala módszereivel. Az ő döntése természetesen nem esik teljesen egybe a miénkkel. Arról nem is beszélve, hogy pusztán retorikai jellegű, meg kell jegyezni például, hogy az első típusú hiányos másodfokú egyenlet megoldása során Al-Khwarizmi, mint minden 17. század előtti matematikus, nem veszi figyelembe a nullát. megoldás, valószínűleg azért, mert konkrét gyakorlati feladatoknál ez nem számít. A teljes másodfokú egyenletek megoldása során Al-Khwarizmi meghatározott numerikus példákkal, majd azok geometriai bizonyításával határozza meg a megoldásukra vonatkozó szabályokat.

Vegyünk egy példát.

4. feladat „A négyzet és a 21 szám egyenlő 10 gyökkel. Keresse meg a gyökeret ”(az x2 + 21 \u003d 10x egyenlet gyökere magában foglalja).

Megoldás: oszd fel a gyökök számát, 5-öt kapsz, 5-öt megszorozod önmagával, a szorzatból kivonsz 21-et, marad 4. Vedd a 4 gyökét, kapsz 2-t. Vonsz ki 2-t 5-ből, kapsz 3-at, ez lesz a kívánt gyökér. Vagy adj hozzá 2-t az 5-höz, ami 7-et ad, ez is egy gyökér.

Al-Khwarizmi értekezése az első olyan könyv, amely eljutott hozzánk, amelyben szisztematikusan bemutatják a másodfokú egyenletek osztályozását, és megadják a megoldásukra vonatkozó képleteket.

Másodfokú egyenletek EurópábanXII- A XVIIV.

A másodfokú egyenletek Al-Khwarizmi mintájára Európában történő megoldásának formáit először az 1202-ben írt "Abacus könyve" írta le. Leonard Fibonacci olasz matematikus. A szerző önállóan dolgozott ki néhány új algebrai problémamegoldási példát, és Európában elsőként közelítette meg a negatív számok bevezetését.

Ez a könyv hozzájárult az algebrai ismeretek elterjedéséhez nemcsak Olaszországban, hanem Németországban, Franciaországban és más európai országokban is. Ebből a könyvből sok feladat átkerült szinte az összes 14-17. századi európai tankönyvbe. A másodfokú egyenletek megoldásának általános szabályát egyetlen kanonikus x2 + bx = c formára redukálva a b, c jelek és együtthatók összes lehetséges kombinációjával, Európában M. Stiefel fogalmazta meg 1544-ben.

Másodfokú egyenlet megoldási képletének levezetése in Általános nézet Vietnek vannak, de Viet csak pozitív gyökereket ismert fel. Tartaglia, Cardano, Bombelli olasz matematikusok az elsők között voltak a 16. században. a pozitív és negatív gyökerek mellett figyelembe kell venni. Csak a XVII. Girard, Descartes, Newton és mások munkáinak köszönhetően tudósok módjára a másodfokú egyenletek megoldása modern formát ölt.

A gyakorlati problémák megoldására szolgáló algebrai módszerek eredete a tudományhoz kapcsolódik ókori világ. A matematikatörténetből ismert, hogy az egyiptomi, sumér, babiloni írnokok-számítógépek által megoldott matematikai jellegű problémák jelentős része (Kr. e. XX-VI. század) számított természetű volt. Azonban már ekkor is felmerültek olyan problémák, amelyekben egy mennyiség kívánt értékét valamilyen közvetett feltétel határozta meg, amely modern szemszögünkből egy egyenlet vagy egyenletrendszer megfogalmazását követeli meg. Kezdetben aritmetikai módszereket alkalmaztak az ilyen problémák megoldására. Később elkezdtek kialakulni az algebrai ábrázolások kezdetei. Például a babiloni számológépek olyan problémákat tudtak megoldani, amelyek csökkenthetőek modern osztályozás másodfokú egyenletekhez. Szöveges feladatok megoldására született egy módszer, amely később az algebrai komponens kiemelésének és önálló vizsgálatának alapjául szolgált.

Ezt a vizsgálatot már egy másik korszakban végezték, először arab matematikusok (Kr. u. VI-X. század), akik rávilágítottak arra a jellegzetes cselekvésre, amellyel az egyenleteket redukálták standard nézet hasonló tagok redukálása, kifejezések áthelyezése az egyenlet egyik részéből a másikba előjelváltással. Aztán a reneszánsz európai matematikusai hosszas keresés eredményeként megalkották a modern algebra nyelvét, a betűhasználatot, az aritmetikai műveletek szimbólumainak bevezetését, zárójeleket stb. A XVI. 17. századok. Az algebra, mint a matematika sajátos része, amelynek megvan a maga tárgya, módszere, alkalmazási területei, már kialakult. Ennek továbbfejlesztése korunkig a módszerek tökéletesítésében, az alkalmazási kör bővítésében, a fogalmak tisztázásában és a matematika más ágai fogalmaival való kapcsolatában állt.

Tehát, tekintettel az egyenlet fogalmához kapcsolódó anyag fontosságára és kiterjedtségére, annak tanulmányozása modern módszertan a matematika eredetének és működésének három fő területéhez kapcsolódik.

Bármely másodfokú egyenlet megoldásához tudnia kell:

a diszkrimináns megtalálásának képlete;

a másodfokú egyenlet gyökereinek megkeresésére szolgáló képlet;

· Algoritmusok az ilyen típusú egyenletek megoldására.

hiányos másodfokú egyenletek megoldása;

teljes másodfokú egyenletek megoldása;

oldja meg a megadott másodfokú egyenleteket;

megtalálni a hibákat a megoldott egyenletekben és kijavítani azokat;

Csinálj egy ellenőrzést.

Minden egyenlet megoldása két fő részből áll:

ennek az egyenletnek a átalakítása a legegyszerűbbre;

szerinti egyenletek megoldása ismert szabályok, képletek vagy algoritmusok.

A tanulók másodfokú egyenletek megoldásában végzett tevékenységének módszereinek általánosítása fokozatosan történik. A következő szakaszok különböztethetők meg a "Kvadratikus egyenletek" téma tanulmányozása során:

I. szakasz - "Nem teljes másodfokú egyenletek megoldása."

II. szakasz - "Teljes másodfokú egyenletek megoldása."

III. szakasz - "A redukált másodfokú egyenletek megoldása."

Az első szakaszban a nem teljes másodfokú egyenleteket veszik figyelembe. Mivel eleinte a matematikusok megtanulták megoldani a hiányos másodfokú egyenleteket, hiszen ehhez nem kellett semmit sem kitalálniuk, ahogy mondják. Ezek a következő alakú egyenletek: ax2 = 0, ax2 + c = 0, ahol c≠ 0, ax2 + bx = 0, ahol b ≠ 0. Tekintsük több ilyen egyenlet megoldását:

1. Ha ax2 = 0. Az ilyen típusú egyenleteket a következő algoritmus szerint oldjuk meg:

1) keresse meg x2-t;

2) keresse meg x-et.

Például 5x2 = 0 . Ha az egyenlet mindkét oldalát elosztjuk 5-tel, akkor kiderül: x2 = 0, tehát x = 0.

2. Ha ax2 + c = 0, c≠ 0 Az ilyen típusú egyenleteket a következő algoritmus szerint oldjuk meg:

1) mozgassa a kifejezéseket a jobb oldalra;

2) keresse meg az összes számot, amelyek négyzete egyenlő a c számmal.

Például x2 - 5 = 0, Ez az egyenlet ekvivalens az x2 = 5 egyenlettel. Ezért meg kell találni az összes olyan számot, amelyek négyzete egyenlő az 5-ös számmal.gif" width="16" height="19 ">..gif" width=" 16" height="19 src=">, és nincs más gyökere.

3. Ha ах2 + bх = 0, b ≠ 0. Az ilyen egyenleteket a következő algoritmus szerint oldjuk meg:

1) mozgassa ki a közös tényezőt a zárójelekből;

2) keresse meg x1, x2.

Például x2 - 3x \u003d 0. Írjuk át az x2 - 3x \u003d 0 egyenletet x (x - 3) \u003d 0 alakban. Ennek az egyenletnek nyilvánvalóan x1 \u003d 0, x2 \u003d gyökei vannak. nincs más gyöke, mert ha x helyett nullától és 3-tól bármely más számot helyettesítünk, akkor az x (x - 3) \u003d 0 egyenlet bal oldalán olyan számot kapunk, amely nem egyenlő nullával.

Tehát ezek a példák bemutatják, hogyan oldják meg a nem teljes másodfokú egyenleteket:

1) ha az egyenlet alakja ax2 = 0, akkor egy gyöke van x = 0;

2) ha az egyenlet alakja ax2 + bx = 0, akkor a faktorizációs módszert alkalmazzuk: x (ax + b) = 0; tehát vagy x = 0 vagy ax + b = 0..gif" width="16" height="41"> Abban az esetben, ha -< 0, уравнение х2 = - не имеет корней (значит, не имеет корней и исходное уравнение ах2 + с = 0). В случае, когда - >0, azaz - = m, ahol m>0, az x2 = m egyenletnek két gyöke van

https://pandia.ru/text/78/002/images/image010_9.gif" width="29" height="24 src=">.gif" width="29" height="24 src=">, (ebben az esetben a rövidebb = jelölés megengedett.

Tehát egy nem teljes másodfokú egyenletnek két gyöke lehet, egy gyöke, nincs gyöke.

A második szakaszban megtörténik az átmenet a teljes másodfokú egyenlet megoldására. Ezek ax2 + bx + c = 0 alakú egyenletek, ahol a, b, c adott számok, a ≠ 0, x az ismeretlen.

Bármely teljes másodfokú egyenlet átalakítható alakra , annak érdekében, hogy meghatározzuk egy másodfokú egyenlet gyökeinek számát, és megtaláljuk ezeket a gyököket. A teljes másodfokú egyenletek megoldásának következő eseteit vizsgáljuk: D< 0, D = 0, D > 0.

1. Ha D< 0, то квадратное уравнение ах2 + bx + c = 0 не имеет действительных корней.

Például 2x2 + 4x + 7 = 0. Megoldás: itt a = 2, b = 4, c = 7.

D \u003d b2 - 4ac \u003d 42 - 4 * 2 * 7 \u003d 16 - 56 \u003d - 40.

Mivel D< 0, то данное квадратное уравнение не имеет корней.

2. Ha D \u003d 0, akkor az ax2 + bx + c \u003d 0 másodfokú egyenletnek egy gyöke van, amelyet a képlet talál meg.

Például 4x - 20x + 25 = 0. Megoldás: a = 4, b = - 20, c = 25.

D \u003d b2 - 4ac \u003d (-20) 2 - 4 * 4 * 25 = 400 - 400 \u003d 0.

Mivel D = 0, ennek az egyenletnek egy gyöke van. Ez a gyökér a ..gif" width="100" height="45">.gif" width="445" height="45 src="> képlet segítségével található.

Összeállítunk egy algoritmust egy ax2 + bx + c = 0 alakú egyenlet megoldására.

1. Számítsa ki a D diszkriminánst a D = b2 - 4ac képlet segítségével.

2. Ha D< 0, то квадратное уравнение ах2 + bx + c = 0 не имеет корней.

3. Ha D = 0, akkor a másodfokú egyenletnek egy gyöke van, amelyet a képlet talál

4..gif" width="101" height="45">.

Ez az algoritmus univerzális, nem teljes és teljes másodfokú egyenletekre egyaránt alkalmazható. A nem teljes másodfokú egyenleteket azonban ez az algoritmus általában nem oldja meg.

A matematikusok gyakorlatias, gazdaságos emberek, ezért a következő képletet használják: https://pandia.ru/text/78/002/images/image022_5.gif" width="155" height="53">. (4)

2..gif" width="96" height="49 src=">, amelynek előjele megegyezik a D-vel..gif" width="89" height="49"> akkor a (3) egyenletnek két gyöke van ;

2) ha akkor az egyenletnek két egybeeső gyöke van;

3) ha akkor az egyenletnek nincs gyöke.

A másodfokú egyenletek tanulmányozásának fontos pontja a Vieta-tétel figyelembe vétele, amely kimondja, hogy a redukált másodfokú egyenlet gyökei és együtthatói között van kapcsolat.

Vieta tétele. Az adott másodfokú egyenlet gyökeinek összege egyenlő a második együtthatóval. ellenkező előjel, és a gyökök szorzata egyenlő a szabad taggal.

Más szavakkal, ha x1 és x2 az x2 + px + q = 0 egyenlet gyöke, akkor

Ezeket a képleteket Vieta formuláknak nevezik F. Vieta () francia matematikus tiszteletére, aki bevezette az algebrai szimbólumok rendszerét, kidolgozta az elemi algebra alapjait. Ő volt az elsők között, aki elkezdte a számokat betűkkel jelölni, ami jelentősen továbbfejlesztette az egyenletelméletet.

Például a fenti x2 - 7x +10 \u003d 0 egyenletnek 2 és 5 gyöke van. A gyökök összege 7, a szorzat pedig 10. Látható, hogy a gyökök összege egyenlő a második együtthatóval. , ellenkező előjellel vettük, és a gyökök szorzata egyenlő a szabad taggal.

Van Vieta tételének ellentétes tétele is.

Tétel fordítottja Vieta tételének. Ha az (5) képletek érvényesek az x1, x2, p, q számokra, akkor x1 és x2 az x2 + px + q = 0 egyenlet gyöke.

Vieta tételét és inverz tételét gyakran használják különféle problémák megoldására.

Például. Írjuk fel a megadott másodfokú egyenletet, melynek gyöke az 1 és a -3 szám.

Vieta képletei szerint

– p = x1 + x2 = - 2,

Ezért a kívánt egyenlet x2 + 2x - 3 = 0.

A Vieta-tétel elsajátításának bonyolultsága több körülményhez kapcsolódik. Mindenekelőtt figyelembe kell venni a direkt és az inverz tételek közötti különbséget. Vieta közvetlen tételében egy másodfokú egyenlet és gyökei adottak; az inverzben csak két szám van, és a másodfokú egyenlet megjelenik a tétel végén. A tanulók gyakran elkövetik azt a hibát, hogy érvelésüket a direkt vagy inverz Vieta-tételre való helytelen hivatkozással támasztják alá.

Például egy másodfokú egyenlet gyökeinek kiválasztásával keresésekor az inverz Vieta-tételre kell hivatkozni, nem pedig a közvetlenre, ahogy azt a tanulók gyakran teszik. Ahhoz, hogy Vieta tételeit a nulla diszkriminancia esetére is kiterjesszük, egyet kell értenünk azzal, hogy ebben az esetben a másodfokú egyenletnek két egyenlő gyöke van. Az ilyen megegyezés kényelme a négyzetes trinomiális faktorizálásában nyilvánul meg.

Kutatás

A témán

"Módszerek másodfokú egyenletek megoldására"

Teljesített:
csoport 8 "G" osztály

Munkavezető:
Benkovszkaja Mária Mihajlovna

A projekt céljai és célkitűzései.

1. Mutassuk meg, hogy a matematikának, mint minden más tudománynak, elege van a megfejtetlen rejtélyeiből.
2. Hangsúlyozza, hogy a matematikusokat a nem szabványos gondolkodás jellemzi. És néha szellemesség és intuíció jó matematikus egyszerűen csodálatosak!
3. Mutassuk meg, hogy a másodfokú egyenletek megoldására tett kísérlet is hozzájárult új matematikai fogalmak és ötletek kifejlesztéséhez!
4. Tanuljon meg különböző információforrásokkal dolgozni.
5. A matematikai kutatómunka folytatása

Kutatási szakaszok

1. A másodfokú egyenletek keletkezésének története.

2. Másodfokú egyenlet definíciója és típusai.

3. Másodfokú egyenletek megoldása a diszkrimináns képlet segítségével.

4. Francois Viet és tétele.

5. Együtthatók tulajdonságai másodfokú egyenlet gyökereinek gyors megtalálásához.

6. Gyakorlati tájékozódás.

Egyenletek, tételek révén

Sok problémát megoldottam.

(Chaucer, angol költő, középkorú.)

színpad. A másodfokú egyenletek kialakulásának története.

Az ókorban nemcsak első, hanem másodfokú egyenletek megoldásának igényét a területkereséssel kapcsolatos problémák megoldásának igénye okozta. földterületekés katonai jellegű földmunkákkal, valamint magával a csillagászat és a matematika fejlődésével.

A babilóniaiak Kr.e. 2000 körül tudtak másodfokú egyenleteket megoldani. A babilóniai szövegekben megfogalmazott ezen egyenletek megoldási szabálya lényegében egybeesik a modernekkel, de nem ismert, hogy a babiloniak hogyan találták meg a szabályt. Az eddig talált ékírásos szövegek szinte mindegyike csak a recept formájában megfogalmazott megoldási problémákat ad, a megtalálás módját nem jelzik.

Annak ellenére, hogy Babilonban magas az algebra fejlettsége, az ékírásos szövegekből hiányzik a negatív szám fogalma és a másodfokú egyenletek megoldásának általános módszerei.

Diophantus "Aritmetikája" szisztematikus feladatsort tartalmaz, magyarázatokkal kísérve és egyenletek megfogalmazásával megoldva. különféle fokozatok, de hiányzik belőle az algebra szisztematikus kifejtése.

A másodfokú egyenletekkel kapcsolatos problémák már megtalálhatók az "Aryabhattiam" csillagászati értekezésekben, amelyeket 499-ben állítottak össze. Aryabhatta indiai matematikus és csillagász. Egy másik indiai tudós, Brahmagupta (7. század) felvázolta az egyetlen kanonikus formára redukált másodfokú egyenletek megoldásának általános szabályát:

Al-Khorezmi algebrai értekezése a lineáris és másodfokú egyenletek osztályozását adja meg. A szerzőnek 6 féle egyenlete van. Al-Khwarizmi számára, aki nem ismerte a negatív számokat, az egyes egyenletek tagjai összeadások, nem kivonások. Ugyanakkor a pozitív megoldásokkal nem rendelkező egyenleteket szándékosan nem veszik figyelembe; egy hiányos másodfokú egyenlet megoldása során al-Khwarizmi, mint minden 17. század előtti tudós, nem veszi figyelembe a nulla megoldást.

Al-Khwarizmi értekezése az első olyan könyv, amely eljutott hozzánk, amelyben szisztematikusan bemutatják a másodfokú egyenletek osztályozását és a megoldási képleteket.

A másodfokú egyenletek al-Khwarizmi mintájára Európában történő megoldására szolgáló képleteket először az Abakusz könyve adta meg, amelyet Leonardo Fibonacci olasz matematikus írt 1202-ben. Ezt a terjedelmes munkát a teljesség és a bemutatás egyértelműsége jellemzi. A szerző önállóan dolgozott ki néhány új algebrai feladatmegoldási módszert, és Európában elsőként közelítette meg a negatív számok bevezetését. Könyve hozzájárult az algebrai ismeretek elterjedéséhez nemcsak Olaszországban, hanem Németországban, Franciaországban és más európai országokban is. Az Abakusz könyvéből sok probléma bekerült szinte az összes 16-17. és részben 18. századi európai tankönyvbe.

Általános szabály a másodfokú egyenletek megoldására egyetlen kanonikus alakra redukálva minden lehetséges jelkombinációval együtthatók b,c Európában csak 1544-ben fogalmazta meg M. Stiefel.

Vietának van egy általános levezetése a másodfokú egyenlet megoldására, de Vieta csak pozitív gyököket ismert fel. Tartaglia, Cardano, Bombelli olasz matematikusok a 16. században az elsők között vették figyelembe nemcsak a pozitív, hanem a negatív gyökereket is. Csak a 17. században, Girrard, Descartes, Newton és más tudósok munkáinak köszönhetően, a másodfokú egyenletek megoldásának módszere öltött modern formát.

KIDERÜL:

A másodfokú egyenletekkel kapcsolatos problémák már 499-ben találhatók.

BAN BEN ősi india nyilvános versenyeket rendeztek nehéz feladatok megoldásában - OLIMPIÁDOK .

©2015-2019 oldal
Minden jog a szerzőket illeti. Ez az oldal nem igényel szerzői jogot, de ingyenesen használható.
Az oldal létrehozásának dátuma: 2016-04-11

BEVEZETÉS

Egyenletek egy iskolai algebra tanfolyamon vezető hely. Több időt szentelnek a tanulásuknak, mint az iskolai matematika tanfolyam bármely más témájának. Az egyenletelmélet erőssége abban rejlik, hogy nemcsak elméleti jelentőséggel bír a természeti törvények ismeretében, hanem konkrét gyakorlati célokat is szolgál. A legtöbb probléma a térformákkal és a mennyiségi viszonyokkal való Világ döntésen múlik különféle fajták egyenletek. A megoldási módok elsajátításával az emberek választ találnak rájuk különféle kérdéseket tudomány és technológia (közlekedés, Mezőgazdaság, ipar, kommunikáció stb.). Szintén az egyenletmegoldó képesség kialakítása szempontjából nagy jelentőséggel bír a tanuló önálló munkája az egyenletmegoldás elsajátításában. Bármely téma tanulmányozása során az egyenletek hatékony eszközként használhatók az elméleti ismeretek megszilárdítására, elmélyítésére, megismétlésére és bővítésére, a hallgatók kreatív matematikai tevékenységének fejlesztésére.

A modern világban az egyenleteket széles körben használják a matematika különböző ágaiban, fontos alkalmazott problémák megoldásában. Ezt a témát a bemutatás nagy mélysége és a tanulásban az ennek segítségével létrejött összefüggések gazdagsága, az előadás logikai érvényessége jellemzi. Ezért kivételes helyet foglal el az egyenletek sorában. A „Négyzet trinomiumok” témakör tanulmányozásába a hallgatók már némi tapasztalatot szerezve, meglehetősen nagy algebrai és általános matematikai fogalmak, fogalmak és készségek birtokában kezdenek el tanulni. Jelentős mértékben a téma anyagán van szükség az egyenletekkel kapcsolatos anyag szintetizálására, a historizmus és az akadálymentesítés elveinek megvalósítására.

Relevancia A téma a historizmus alapelvei megvalósításának szükségessége és ennek megvalósításához szükséges anyag hiánya a "Másodfokú egyenletek megoldása" témakörben.

Kutatási probléma: történelmi anyag azonosítása a másodfokú egyenletek megoldásának megtanulásához.

A munka célja: ötletek kialakítása a másodfokú egyenletek matematika órákon történő feldolgozásával kapcsolatban, a historizmus elemeit tartalmazó leckekészlet kiválasztása a "Kvadrális egyenletek" témában.

A vizsgálat tárgya: másodfokú egyenletek megoldása 8. osztályban a historizmus elemeinek felhasználásával.

Tanulmányi tárgy: másodfokú egyenletek és leckék kidolgozása a másodfokú egyenletek történeti anyagok felhasználásával történő megoldásának megtanulásához.

Feladatok:

elvégzi a kutatási probléma tudományos és módszertani szakirodalmának elemzését;

elemezze az iskolai tankönyveket, és emelje ki bennük a másodfokú egyenletek megoldásának tanulásának helyét;

vegyen fel egy leckét a másodfokú egyenletek történelmi anyagok felhasználásával történő megoldásáról.

Kutatási módszerek:

szakirodalom elemzése a "Másodfokú egyenletek megoldása" témában;

a tanulók megfigyelése a "Másodfokú egyenletek megoldása" témában tartott óra során;

anyagválogatás: leckék a "Másodfokú egyenletek megoldása" témában történelmi hivatkozással.

1. § A másodfokú egyenletek keletkezésének történetéből

Az algebra különféle problémák egyenletekkel történő megoldása kapcsán merült fel. Általában problémák esetén egy vagy több ismeretlent kell találni, miközben ismerjük a kívánt és megadott mennyiségeken végrehajtott egyes műveletek eredményét. Az ilyen feladatok egy vagy több egyenletrendszer megoldására redukálódnak, adott mennyiségeken végzett algebrai műveletek segítségével a kívántak megtalálására. Az algebra a mennyiségekre gyakorolt hatások általános tulajdonságait vizsgálja.

A lineáris és másodfokú egyenletek megoldására szolgáló algebrai technikák már 4000 évvel ezelőtt ismertek voltak az ókori Babilonban.

Másodfokú egyenletek az ókori Babilonban

Az egyenletek megoldására vonatkozó, a babiloni szövegekben megfogalmazott szabály lényegében egybeesik a modernnel, de nem ismert, hogy a babilóniaiak hogyan jutottak el ehhez a szabályhoz. Az eddig talált ékírásos szövegek szinte mindegyike csak a recept formájában megfogalmazott megoldási problémákat ad, a megtalálás módját nem jelzik. Annak ellenére, hogy Babilonban magas az algebra fejlettsége, az ékírásos szövegekből hiányzik a negatív szám fogalma és a másodfokú egyenletek megoldásának általános módszerei.

Az egyenletek összeállításakor Diophantus ügyesen választ ismeretleneket, hogy leegyszerűsítse a megoldást.

Itt van például az egyik feladata.

2. feladat "Keress két számot, tudva, hogy összegük 20, szorzatuk pedig 96."

Diophantus a következőképpen érvel: a feladat feltételéből az következik, hogy a kívánt számok nem egyenlőek, hiszen ha egyenlőek lennének, akkor a szorzatuk nem 96, hanem 100 lenne. Így az egyik több lesz, mint összegük fele, azaz .
. A másik kisebb, pl.
. A különbség köztük
. Ezért az egyenlet:

Innen
. A kívánt számok egyike 12, a másik 8. Megoldás
mert Diophantus nem létezik, mivel a görög matematika csak pozitív számokat ismert.

Ha ezt a feladatot megoldjuk, az egyik ismeretlen számot ismeretlennek választva, akkor eljuthatunk az egyenlet megoldásához:

Másodfokú egyenletek Indiában

A másodfokú egyenletekkel kapcsolatos problémák már megtalálhatók az Aryabhattam csillagászati értekezésben, amelyet Aryabhatta indiai matematikus és csillagász állított össze 499-ben. Egy másik indiai tudós, Brahmagupta (7. század) felvázolta az egyetlen kanonikus formára redukált másodfokú egyenletek megoldásának általános szabályát:

(1)

Az (1) egyenletben az együtthatók negatívak is lehetnek. Brahmagupta uralma lényegében egybeesik a miénkkel.

Indiában gyakoriak voltak a nyilvános versenyek a nehéz problémák megoldásában. Az egyik régi indiai könyvben a következőt mondják az ilyen versenyekről: „Ahogy a nap ragyogó fényével felülmúlja a csillagokat, úgy a tanult ember is felülmúlja a dicsőséget a nyilvános üléseken, ahol algebrai feladatokat javasol és old meg.” A feladatokat gyakran költői formába öltöztették.

Itt van a XII. század híres indiai matematikusának egyik problémája. Bhaskara.

Bhaskara megoldása azt jelzi, hogy a szerző tisztában volt a másodfokú egyenletek gyökereinek kétértékűségével.

A 3. feladatnak megfelelő egyenlet:

Bhaskara ezt írja leple alatt:

és hogy ennek az egyenletnek a bal oldalát a négyzethez egészítse ki, mindkét oldalához hozzáad 322-t, így kapja:

Al-Khwarizmi másodfokú egyenletei

Al-Khwarizmi algebrai értekezése a lineáris és másodfokú egyenletek osztályozását adja meg. A szerző 6 típusú egyenletet sorol fel, ezeket a következőképpen fejezi ki:

Vegyünk egy példát.

4. feladat „A négyzet és a 21 szám egyenlő 10 gyökkel. Keresse meg a "gyököt" (az egyenlet gyökerét jelenti
).

Másodfokú egyenletek EurópábanXII- A XVIIV.

Ez a könyv hozzájárult az algebrai ismeretek elterjedéséhez nemcsak Olaszországban, hanem Németországban, Franciaországban és más európai országokban is. Ebből a könyvből sok feladat átkerült szinte az összes 14-17. századi európai tankönyvbe. Általános szabály a másodfokú egyenletek megoldására egyetlen kanonikus alakra redukálva
a b, c jelek és együtthatók minden lehetséges kombinációjával, 1544-ben fogalmazta meg Európában M. Stiefel.

Vietának van egy általános levezetése a másodfokú egyenlet megoldására, de Vieta csak pozitív gyököket ismert fel. Tartaglia, Cardano, Bombelli olasz matematikusok az elsők között voltak a 16. században. a pozitív és negatív gyökerek mellett figyelembe kell venni. Csak a XVII. Girard, Descartes, Newton és más tudósok munkáinak köszönhetően a másodfokú egyenletek megoldásának módszere modern formát ölt.

A gyakorlati problémák megoldására szolgáló algebrai módszerek eredete az ókori világ tudományához kapcsolódik. A matematikatörténetből ismert, hogy az egyiptomi, sumér, babiloni írnokok-számítógépek által megoldott matematikai jellegű problémák jelentős része (Kr. e. XX-VI. század) számított természetű volt. Azonban már ekkor is felmerültek olyan problémák, amelyekben egy mennyiség kívánt értékét valamilyen közvetett feltétel határozta meg, amely modern szemszögünkből egy egyenlet vagy egyenletrendszer megfogalmazását követeli meg. Kezdetben aritmetikai módszereket alkalmaztak az ilyen problémák megoldására. Később elkezdtek kialakulni az algebrai ábrázolások kezdetei. Például a babiloni számológépek olyan problémákat tudtak megoldani, amelyek a modern osztályozás szempontjából másodfokú egyenletekre redukálódnak. Szöveges feladatok megoldására született egy módszer, amely később az algebrai komponens kiemelésének és önálló vizsgálatának alapjául szolgált.

Ezt a vizsgálatot már egy másik korszakban végezték el, először arab matematikusok (Kr. u. VI-X. század), akik olyan jellegzetes cselekvéseket jelöltek meg, amelyek révén az egyenletek szabványos formára redukálódnak, a hasonló kifejezések redukálása, a kifejezések áthelyezése az egyik részből. egyenlet egy másik előjelváltozással. Aztán a reneszánsz európai matematikusai hosszas keresés eredményeként megalkották a modern algebra nyelvét, a betűhasználatot, az aritmetikai műveletek szimbólumainak bevezetését, zárójeleket stb. A XVI. 17. századok. Az algebra, mint a matematika sajátos része, amelynek megvan a maga tárgya, módszere, alkalmazási területei, már kialakult. Ennek továbbfejlesztése korunkig a módszerek tökéletesítésében, az alkalmazási kör bővítésében, a fogalmak tisztázásában és a matematika más ágai fogalmaival való kapcsolatában állt.

Tehát, tekintettel az egyenlet fogalmához kapcsolódó anyag fontosságára és kiterjedtségére, a matematika modern módszertanában való tanulmányozása az előfordulásának és működésének három fő területéhez kapcsolódik.

Kezdőlap > Jelentés

Hősökről elnevezett MOU középiskola szovjet Únió
Sotnikova A.T. és Shepeleva N. G. s. Uritskoe

Beszámoló a témáról:

"A megjelenés története

másodfokú egyenletek"

Készítette:Izotova Julia,
Ampleeva Elena,
Nyikolaj Sepelev,

Djacsenko Jurij.

Ó, matematika. Évszázadokon át borít a dicsőség,

Minden földi világítótest lámpása.

Te fenséges királynő

Nem csoda, hogy Gauss megkeresztelkedett.

Szigorú, logikus, fenséges,

Repülés közben karcsú, mint egy nyíl,

Örök dicsőséged

Az idők során halhatatlanságra tett szert.

Dicsérjük az emberi elmét

a tetteit varázs kezek,

E kor reménysége

Minden földi tudomány királynője.

Ma szeretnénk elmondani

Előfordulás története

Amit minden diáknak tudnia kell

A másodfokú egyenletek története.

Eukleidész, a Kr.e. III. században. e. a geometriai algebrának szentelt "Elvek"-ben a teljes második könyvet, amely minden szükséges anyagot tartalmaz a másodfokú egyenletek megoldásához.

Euklidész (Eνκλειδηζ), ókori görög matematikus, az első hozzánk eljutott matematikai elméleti értekezés szerzője

Euklidészről rendkívül kevés információ áll rendelkezésre. Az egyetlen dolog, ami megbízhatónak tekinthető, az tudományos tevékenység az ie III. században Alexandriában folyt. e. Eukleidész az alexandriai iskola első matematikusa. Övé fő munka A "Kezdetek" (latinizált formában - "Elemek") a planimetria, a sztereometria és számos számelméleti kérdés bemutatását tartalmazza; benne foglalta össze a görög matematika korábbi fejlődését és megteremtette az alapot további fejlődés matematika. Gém - Görög matematikus és mérnök először Görögországban a Kr.u. I. században. tisztán algebrai módszert ad a másodfokú egyenlet megoldására.

Alexandriai gém; Heron, I c. n. e., görög mechanikus és matematikus. Életének ideje bizonytalan, csak annyit tudni, hogy Arkhimédészt (aki Kr. e. 212-ben halt meg), őt magát Pappus (i.sz. 300 körül) idézte. Jelenleg az a vélemény uralkodik, hogy az I. században élt. n. e. Geometriát, mechanikát, hidrosztatikát, optikát tanult; feltalálta a gőzgép prototípusát és a precíziós szintező műszereket. A legnépszerűbb automaták az automata színházak, szökőkutak és egyebek voltak.G. a statika és a kinetika törvényeire támaszkodva leírta a teodolitot, leírást adott a karról, a blokkról, a propellerről és a katonai járművekről. Az optikában a fényvisszaverődés törvényeit fogalmazta meg, a matematikában - a legfontosabb mérési módszereket. geometriai formák. G. fő művei az Etrika, Pneumatika, Autopoietika, Mechanika (francia; a mű teljes egészében arabul őrződött meg), a Katoptika (a tükrök tudománya; csak Latin fordítás) és mások.. G. felhasználta elődei vívmányait: Euklidész, Arkhimédész, Lampsakból származó Strato. Stílusa egyszerű és világos, bár néha túl lakonikus vagy strukturálatlan. G. írásai iránti érdeklődés a III. n. e. Görög, majd bizánci és arab diákok kommentálták és fordították műveit.

Diophantus- egy görög tudós a Kr.u. 3. században, anélkül, hogy a geometriához folyamodott volna, néhány másodfokú egyenletet tisztán algebrai módon oldott meg, és magát az egyenletet és megoldását szimbolikus formában írták le.

„Elmondom, hogyan alkotott és oldott meg másodfokú egyenleteket a görög matematikus, Diophantus. Itt van például az egyik feladata:"Keress két számot úgy, hogy az összegük 20, a szorzatuk pedig 96."

1. A feladat feltételéből következik, hogy a kívánt számok nem egyenlőek, mert ha egyenlőek lennének, akkor a szorzatuk nem 96, hanem 100 lenne.

2. Így. egyikük több mint a fele lesz az összegüknek, i.e. 10 + x, a másik kisebb, azaz. 10 - x.

3. A különbség köztük 2x.

4. Ebből adódik a (10 + x) * (10 - x) = 96 egyenlet

100 - x 2 = 96 x 2 - 4 = 0

5. Válasz x = 2. A kívánt számok egyike a 12,
egyéb - 8. Az x = - 2 megoldás Diophantus esetében nem létezik, mert A görög matematika csak pozitív számokat ismert. Diophantus tudta, hogyan kell megoldani nagyon összetett egyenleteket, amelyeket ismeretlenekre használtak betűjelölések, bevezetett egy speciális szimbólumot a számításhoz, szórövidítéseket használt. Bhaskare – Akaria- Indiai matematikus a XII. században. felfedezett egy általános módszert a másodfokú egyenletek megoldására.

Elemezzük az indiai matematikusok egyik problémáját, például Bhaskara problémáját:

„Egy nyáj majom szórakozik: nyolcaduk egy négyzeten tréfálkodik az erdőben, a maradék tizenkettő a halom tetején sikít. Mondd, hány majom van?

A feladatot kommentálva azt szeretném mondani, hogy az (x/8) 2 + 12 = x egyenlet felel meg a feladatnak. Bhaskara x 2 - 64x \u003d - 768 alakot ír. Ha mindkét részhez hozzáadjuk a 32-es négyzetet, az egyenlet a következőképpen alakul:

x 2 - 64 x + 32 2 = - 768 + 1024

(x - 32) 2 = 256

A négyzetgyök kinyerése után a következőt kapjuk: x - 32 = 16.

"BAN BEN ez az eset, mondja Bhaskara, - az első rész negatív egységei olyanok, hogy a második rész egységei kisebbek náluk, és ezért az utóbbit tekinthetjük pozitívnak és negatívnak is, és megkapjuk az ismeretlen kettős értékét: 48 ill. 16.

Meg kell állapítani, hogy Bhaskara megoldása azt jelzi, hogy tudott a másodfokú egyenletek gyökereinek kétértékűségéről.

A régi indiai Bhaskara probléma megoldását javasolják:

„A majmok egyötödének négyzete hárommal csökkentve megbújt a barlangban, egy majom felmászott egy fára, látszott. Hány majom volt? Meg kell jegyezni, hogy ez a probléma elemileg megoldott, másodfokú egyenletre redukálva.

Al - Khorezmi - egy arab tudós, aki 825-ben megírta a "A helyreállítás és az ellenállás könyve" című könyvet. Ez volt a világ első algebrai tankönyve. Hatféle másodfokú egyenletet is adott, és mind a hat egyenletre, amelyeket verbális formában fogalmazott meg, egy speciális szabályt ennek megoldására. A dolgozatban Khorezmi 6 típusú egyenletet sorol fel, ezeket a következőképpen fejezi ki:

1. "A négyzetek egyenlőek a gyökökkel", azaz. ax 2 = in.

2. "A négyzetek egyenlőek a számmal", azaz. ax 2 = s.

3. "A gyökök egyenlőek a számmal", azaz. ah = s.

4. "A négyzetek és a számok egyenlőek a gyökekkel", azaz. ax 2 + c \u003d be.

5. "A négyzetek és a gyökök egyenlőek a számmal", azaz. ax 2 + in = s.

6. "A gyökök és a számok egyenlőek a négyzetekkel", azaz. in + c \u003d ah 2.

Elemezzük al-Khwarizmi problémáját, amely egy másodfokú egyenlet megoldására redukálódik. "Egy négyzet és egy szám egyenlő a gyökekkel." Például egy négyzet és a 21-es szám egyenlő ugyanannak a négyzetnek 10 gyökével, azaz. a kérdés az, hogy miből alakul ki egy négyzet, amelyhez 21-et hozzáadva egyenlő lesz ugyanannak a négyzetnek a 10 gyökével?

ÉS al-Khwarizmi 4. képletével a tanulóknak fel kell írniuk: x 2 + 21 = 10x

François Viet - francia matematikus, megfogalmazta és bebizonyította az adott másodfokú egyenlet gyökeinek összegére és szorzatára vonatkozó tételt.

Az általam bemutatott művészet új, vagy legalábbis annyira elrontotta a barbárok hatása, hogy jónak láttam teljesen új külsőt adni.

François Viet

Pedig François (1540-13.12.1603) Fontenay-le-Comte városában született Poitou tartományban, nem messze a híres La Rochelle erődtől. Jogi diploma megszerzése után tizenkilenc éves korától sikeresen praktizált ügyvédként szülőváros. Ügyvédként Viet tekintélyt és tiszteletet élvezett a lakosság körében. Széleskörűen művelt ember volt. Ismerte a csillagászatot, a matematikát és minden mást Szabadidő adott ezeknek a tudományoknak.

Fő szenvedély Vieta matematika volt. Mélyen tanulmányozta Arkhimédész és Diophantus klasszikusok műveit, Cardano, Bombelli, Stevin és mások közvetlen elődjeit. Vieta nemcsak csodálta őket, hanem egy nagy hibát is látott bennük, ami a verbális szimbolikából adódó megértés nehézsége volt: Szinte minden cselekvést és jelet szavakkal rögzítettek, nyoma sem volt azoknak a kényelmes, szinte automatikus szabályoknak, amelyeket most használunk. . Lehetetlen volt leírni, és ezért általános formában elkezdeni algebrai összehasonlításokat vagy bármilyen más algebrai kifejezést. Minden numerikus együtthatós egyenlettípust egy speciális szabály szerint oldottak meg. Ezért be kellett bizonyítani, hogy vannak általános akciók minden olyan számon, amely nem függ ezektől a számoktól. Viet és követői megállapították, hogy nem mindegy, hogy a szóban forgó szám az objektumok száma vagy a szakasz hossza. A lényeg az, hogy ezekkel a számokkal lehet algebrai műveleteket végrehajtani, és ennek eredményeként ismét ugyanolyan számokat kapni. Ezért néhány absztrakt jellel jelölhetők. Viet pont ezt tette. Nemcsak bevezette a szó szerinti számítását, hanem egy alapvetően új felfedezést tett, és azt a célt tűzte ki maga elé, hogy ne a számokat, hanem az azokon végzett cselekvéseket tanulmányozza. Ez az írásmód lehetővé tette Vietának, hogy fontos felfedezéseket tegyen az algebrai egyenletek általános tulajdonságainak tanulmányozásában. Nem véletlenül nevezik Vietát az algebra "atyjának", a betűszimbólumok megalapítójának.

Információs források:

http :// som. fio. hu/ erőforrások/ Karpuhina/2003/12/ Befejezve%20 munka/ Koncert/ index1. htm

http :// oldalakat. marsu. hu/ iac/ iskola/ s4/ oldalon74. html

Az Orosz Föderáció Oktatási Minisztériuma

Önkormányzati oktatási intézmény

"22-es középiskola"

Másodfokú és magasabb rendű egyenletek

Elkészült:

8 "B" osztály tanulói

Kuznyecov Jevgenyij és Rudy Alexey

Felügyelő:

Zenina Alevtina Dmitrievna

matematika tanár

Bevezetés

1.1 Egyenletek az ókori Babilonban

1.2 Az arabok egyenletei

1.3 Egyenletek Indiában

2. fejezet Másodfokú egyenletek és magasabb rendű egyenletek elmélete

2.1 Alapfogalmak

2.2 Páros együttható képletek x-hez

2.3 Vieta tétele

2.4 Különleges természetű másodfokú egyenletek

2.5 Vieta tétele magasabb fokú polinomokra (egyenletekre).

2.6 Négyzetekre redukálható egyenletek (kétnegyedes)

2.7 Biquadratic egyenletek tanulmányozása

2.8 Cordano képletek

2.9 Harmadfokú szimmetrikus egyenletek

2.10 Visszatérési egyenletek

2.11 Horner séma

Következtetés

Bibliográfia

1. számú melléklet

2. melléklet

3. függelék

Bevezetés

Az algebra iskolai kurzusában az egyenletek vezető helyet foglalnak el. Több időt vesz igénybe a tanulás, mint bármely más téma. Valójában az egyenleteknek nemcsak fontos elméleti jelentősége van, hanem pusztán gyakorlati célokat is szolgálnak. A való világ térbeli formáival és mennyiségi viszonyaival kapcsolatos problémák túlnyomó többsége különféle típusú egyenletek megoldására redukálódik. Megoldásuk módjait elsajátítva választ kapunk a tudomány és a technológia különböző kérdéseire (közlekedés, mezőgazdaság, ipar, hírközlés stb.).

Ebben az esszében szeretném bemutatni a különböző egyenletek megoldási képleteit és módszereit. Ehhez olyan egyenleteket adunk meg, amelyeket az iskolai tanterv nem tanulmányoz. Alapvetően ezek sajátos természetű és magasabb fokú egyenletek. Ennek a témának a feltárására e képletek bizonyítékait adjuk meg.

Kivonatunk céljai:

Fejlessze az egyenletmegoldási készségeket

Új módszerek kidolgozása az egyenletek megoldására

Tanuljon meg néhány új módszert és képletet ezen egyenletek megoldására.

A vizsgálat tárgya az elemi algebra, a vizsgálat tárgya az egyenlet. Ennek a témakörnek a megválasztása azon alapult, hogy mind az alapprogramban, mind az azt követő órákon vannak egyenletek. általános oktatási iskolák, líceumok, főiskolák. Számos geometriai, fizika, kémia és biológia problémát egyenletek segítségével oldanak meg. Az egyenleteket huszonöt évszázaddal ezelőtt oldották meg. Még ma is készítik őket – mindkettő felhasználásra oktatási folyamat, valamint az egyetemi versenyvizsgákra, a legmagasabb szintű olimpiára.

1. fejezet Másodfokú egyenletek és magasabb rendű egyenletek története

1.1 Egyenletek az ókori Babilonban

Az algebra különféle problémák egyenletekkel történő megoldása kapcsán merült fel. Általában problémák esetén egy vagy több ismeretlent kell találni, miközben ismerjük a kívánt és megadott mennyiségeken végrehajtott egyes műveletek eredményét. Az ilyen feladatok egy vagy több egyenletrendszer megoldására redukálódnak, adott mennyiségeken végzett algebrai műveletek segítségével a kívántak megtalálására. Az algebra a mennyiségekre gyakorolt hatások általános tulajdonságait vizsgálja.

A lineáris és másodfokú egyenletek megoldására szolgáló algebrai technikák már 4000 évvel ezelőtt ismertek voltak az ókori Babilonban. Az ókorban nemcsak az első, hanem a másodfokú egyenletek megoldásának szükségességét a földterületek felkutatásával és a katonai jellegű földmunkákkal, valamint a csillagászat fejlődésével kapcsolatos problémák megoldásának igénye okozta. és maga a matematika. Mint korábban említettük, a babilóniaiak tudták, hogyan kell megoldani a másodfokú egyenleteket Kr.e. 2000 körül. A modern algebrai jelölésekkel azt mondhatjuk, hogy hiányos és teljes másodfokú egyenletek egyaránt előfordulnak ékírásos szövegeikben.

Ezen egyenletek megoldásának szabálya, amely a babiloni szövegekben szerepel, lényegében egybeesik a modernekkel, de nem ismert, hogy a babilóniaiak hogyan jutottak el ehhez a szabályhoz. Az eddig talált ékírásos szövegek szinte mindegyike csak a recept formájában megfogalmazott megoldási problémákat ad, a megtalálás módját nem jelzik.

Annak ellenére, hogy Babilonban az algebra magas fejlettségi szintje van, az ékírásos szövegekben nem létezik negatív szám fogalma és általános módszerek a másodfokú egyenlet megoldására.

1.2 Az arabok egyenletei

Az egyenletek megoldásának néhány módszerét, mind a másodfokú, mind a magasabb fokú egyenleteket az arabok származtatták. Tehát a híres arab matematikus, Al-Khwarizmi "Al-Jabar" című könyvében számos módot írt le a különböző egyenletek megoldására. Különlegességük az volt, hogy Al-Khwarizmi összetett gyököket használt az egyenletek gyökereinek (megoldásának) megtalálásához. Az ilyen egyenletek megoldásának szükségessége az öröklés megosztásával kapcsolatos kérdésekben volt szükséges.

1.3 Egyenletek Indiában

A másodfokú egyenleteket Indiában is megoldották. A másodfokú egyenletekkel kapcsolatos problémák már megtalálhatók az Aryabhattam csillagászati értekezésben, amelyet Aryabhatta indiai matematikus és csillagász állított össze 499-ben. Egy másik indiai tudós, Brahmagupta (7. század) felvázolt egy általános szabályt az egyetlen kúpos alakra redukált másodfokú egyenletek megoldására:

ax² + bx= c, ahol a > 0

Ebben az egyenletben az együtthatók az a kivételével negatívak is lehetnek. Brahmagupta uralma lényegében egybeesik a miénkkel.

Az ókori Indiában gyakoriak voltak a nyilvános versenyek a nehéz problémák megoldásában. Az egyik régi indiai könyv a következőt írja az ilyen versenyekről: „Ahogy a nap ragyogó fényével felülmúlja a csillagokat, úgy a tanult ember is felülmúlja a másik dicsőségét a nyilvános üléseken, algebrai feladatokat javasolva és megoldva”. A feladatokat gyakran költői formába öltöztették.

Különféle egyenleteket, másodfokú és magasabb fokú egyenleteket is megoldottak távoli őseink. Ezeket az egyenleteket a legkülönbözőbb és egymástól legtávolabbi országokban oldották meg. Nagy szükség volt az egyenletekre. Az egyenleteket az építőiparban, a katonai ügyekben és a mindennapi helyzetekben használták.

2. fejezet Másodfokú és magasabb rendű egyenletek

2.1 Alapfogalmak

A másodfokú egyenlet a forma egyenlete

ahol az a, b, c együtthatók tetszőleges valós számok, és a ≠ 0.

A másodfokú egyenletet redukáltnak nevezzük, ha a vezető együtthatója 1.

Példa :

x2 + 2x + 6 = 0.

A másodfokú egyenletet nem redukáltnak nevezzük, ha a vezető együttható eltér 1-től.

Példa :

2x2 + 8x + 3 = 0.

A teljes másodfokú egyenlet olyan másodfokú egyenlet, amelyben mindhárom tag jelen van, más szóval ez egy olyan egyenlet, amelyben a b és c együttható értéke nem nulla.

Példa :

3x2 + 4x + 2 = 0.

A nem teljes másodfokú egyenlet olyan másodfokú egyenlet, amelyben legalább egy b, c együttható nullával egyenlő.

Így háromféle nem teljes másodfokú egyenlet létezik:

1) ax² = 0 (két azonos gyöke van x = 0).

2) ax² + bx = 0 (két gyöke van: x 1 = 0 és x 2 = -)

Példa :

x 1 = 0, x 2 = -5.

Válasz: x 1 \u003d 0, x 2 \u003d -5.

Ha -<0 - уравнение не имеет корней.

Példa :

Válasz: az egyenletnek nincs gyöke.

Ha –> 0, akkor x 1,2 = ±

Példa :

Válasz: x 1,2 =±

Bármely másodfokú egyenlet megoldható a diszkriminánssal (b² - 4ac). Általában a b² - 4ac kifejezést D betűvel jelöljük, és az ax² + bx + c = 0 másodfokú egyenlet diszkriminánsának (vagy az ax² + bx + c négyzet háromtagú diszkriminánsának) nevezik.

Példa :

x 2 +14x - 23 = 0

D \u003d b 2 - 4ac \u003d 144 + 92 \u003d 256

x 2 =

Válasz: x 1 = 1, x 2 = - 15.

A diszkriminánstól függően az egyenletnek lehet megoldása, de lehet, hogy nem.

1) Ha D< 0, то не имеет решения.

2) Ha D = 0, akkor az egyenletnek két egybeeső megoldása van x 1,2 =

3) Ha D > 0, akkor két megoldása van, amelyeket a következő képlettel találunk:

x 1,2 =

2.2 Páros együttható képletek x-hez

Megszoktuk, hogy a másodfokú egyenlet gyökerei

ax² + bx + c = 0 a képlet alapján találhatók

x 1,2 =

A matematikusok azonban soha nem hagyják el a lehetőséget, hogy megkönnyítsék számításaikat. Azt találták, hogy ez a képlet egyszerűsíthető, ha a b együttható b = 2k alakú, különösen, ha b páros szám.

Valóban, legyen az ax² + bx + c = 0 másodfokú egyenlet b együtthatója b = 2k alakú. Ha a képletünkbe behelyettesítjük a 2k számot b helyett, a következőt kapjuk:

Tehát az ax² + 2kx + c = 0 másodfokú egyenlet gyökerei a következő képlettel számíthatók ki:

x 1,2 =

Példa :

5x 2 - 2x + 1 = 0

Ennek a képletnek az az előnye, hogy nem a b szám négyzetes, hanem a fele, nem 4ac, hanem egyszerűen ac kivonásra kerül ebből a négyzetből, és végül, hogy a nevezőben nem 2a, hanem egyszerűen a szerepel.

Ha a másodfokú egyenlet adott, akkor a képletünk így fog kinézni:

Példa :

x 2 - 4x + 3 = 0

Válasz: x 1 = 3, x 2 = 1.

2.3 Vieta tétele

Francois Viet francia matematikus fedezte fel a másodfokú egyenlet gyökereinek egy nagyon furcsa tulajdonságát. Ezt a tulajdonságot Vieta tételének nevezzük:

Tehát az x 1 és x 2 számok az egyenlet gyökerei:

ax² + bx + c = 0

szükséges és elégséges, hogy az egyenlőség

x 1 + x 2 = -b/a és x 1 x 2 = c/a

Vieta tétele lehetővé teszi a másodfokú egyenlet előjeleinek és abszolút értékének megítélését

x² + bx + c = 0

1. Ha b>0, c>0, akkor mindkét gyök negatív.

2. Ha b<0, c>0, akkor mindkét gyök pozitív.

3. Ha b>0, c<0 то уравнение имеет корни разных знаков, причём отрицательный корень по абсолютной величине больше положительного.

4. Ha b<0, c<0 то уравнение имеет корни разных знаков, причём отрицательный корень по абсолютной величине меньше положительного.

2.4 Különleges természetű másodfokú egyenletek

1) Ha a + b + c = 0 az ax² + bx + c = 0 egyenletben, akkor

x 1 \u003d 1 és x 2 \u003d.

Bizonyíték :

Az ax² + bx + c = 0 egyenletben a gyökei

x 1,2 = (1).

Képviseljük b-t az a + b + c = 0 egyenlőségből

Ezt a kifejezést behelyettesítjük az (1) képletbe:

Ha az egyenlet két gyökerét külön-külön vesszük figyelembe, akkor a következőt kapjuk:

1) x 1 =

2) x 2 =

Ebből következik: x 1 \u003d 1 és x 2 \u003d.

1. Példa :

2x² - 3x + 1 = 0

a=2, b=-3, c=1.

a + b + c = 0, tehát

2. Példa :

418x² - 1254x + 836 = 0

Ezt a példát nagyon nehéz a diszkriminánson keresztül megoldani, de a fenti képlet ismeretében könnyen megoldható.

a=418, b=-1254, c=836.

x 1 = 1 x 2 = 2

2) Ha a - b + c = 0, az ax² + bx + c = 0 egyenletben, akkor:

x 1 \u003d -1 és x 2 \u003d -.

Bizonyíték :

Tekintsük az ax² + bx + c = 0 egyenletet, ami azt jelenti, hogy:

x 1,2 = (2).

Képviseljük b-t az a - b + c = 0 egyenlőségből

b = a + c, helyettesítsd be a (2) képletbe:

Két kifejezést kapunk:

1) x 1 =

2) x 2 =

Ez a képlet hasonló az előzőhöz, de azért is fontos, mert. gyakran van példa erre a típusra.

1) Példa :

2x² + 3x + 1 = 0

a = 2, b = 3, c = 1.

a - b + c = 0, tehát

2)Példa :

Válasz: x 1 \u003d -1; x 2 = -

3) "módszer" transzferek ”

Az y² + by + ac = 0 és ax² + bx + c = 0 másodfokú egyenletek gyökereit a következő összefüggések kapcsolják össze:

x 1 = és x 2 =

Bizonyíték :

a) Tekintsük az ax² + bx + c = 0 egyenletet

x 1,2 = =

b) Tekintsük az y² + x + ac = 0 egyenletet

y 1,2 =

Figyeljük meg, hogy mindkét megoldás diszkriminánsai egyenlőek, hasonlítsuk össze e két egyenlet gyökereit. A vezető együtthatóban különböznek egymástól, az első egyenlet gyökei a-val kisebbek, mint a másodiké. A Vieta-tételt és a fenti szabályt felhasználva nem nehéz különféle egyenleteket megoldani.

Példa :

Van egy tetszőleges másodfokú egyenletünk

10x² - 11x + 3 = 0

Ezt az egyenletet a fenti szabály szerint alakítjuk át

y² - 11 év + 30 = 0

Megkapjuk a redukált másodfokú egyenletet, amely könnyen megoldható Vieta tételével.

Legyen y 1 és y 2 az y² - 11y + 30 = 0 egyenlet gyöke

y 1 y 2 = 30 y 1 = 6

y 1 + y 2 = 11 y 2 = 5

Tudva, hogy ezen egyenletek gyökerei a-val különböznek egymástól, akkor

x 1 \u003d 6/10 \u003d 0,6

x 2 = 5/10 \u003d 0,5

Bizonyos esetekben célszerű először nem az adott ax² + bx + c = 0 egyenletet megoldani, hanem a + ac = 0-val redukált y² + -t, amelyet az adott a „átviteli” együtthatóból kapunk, majd elosztjuk a talált értéket. gyökezzünk a-val, hogy megtaláljuk az eredeti egyenletet.

2.5 Vieta képlet magasabb fokú polinomokhoz (egyenletekhez).

A Vieta által a másodfokú egyenletekre levezetett képletek magasabb fokú polinomokra is igazak.

Legyen a polinom

P(x) = a 0 x n + a 1 x n -1 + … +a n

N különböző x 1, x 2 …, x n gyöke van.

Ebben az esetben a következő alakzattal rendelkezik:

a 0 x n + a 1 x n-1 +…+ a n = a 0 (x – x 1) (x – x 2)… (x – x n)

Osszuk el ennek az egyenlőségnek mindkét részét 0 ≠ 0-val, és bontsuk ki a zárójeleket az első részben. Az egyenlőséget kapjuk:

x n + ()x n -1 + ... + () = x n - (x 1 + x 2 + ... + x n) x n -1 + (x 1 x 2 + x 2 x 3 + ... + x n -1 x n)x n - 2 + … +(-1) n x 1 x 2 … x n

De két polinom akkor és csak akkor egyenlő, ha az együtthatók azonos hatványokon egyenlők. Ebből az következik, hogy az egyenlőség

x 1 + x 2 + … + x n = -

x 1 x 2 + x 2 x 3 + … + x n -1 x n =

x 1 x 2 … x n = (-1) n

Például a harmadfokú polinomokhoz

a 0 x³ + a 1 x² + a 2 x + a 3

Vannak identitásaink

x 1 + x 2 + x 3 = -

x 1 x 2 + x 1 x 3 + x 2 x 3 =

x 1 x 2 x 3 = -

Ami a másodfokú egyenleteket illeti, ezt a képletet Vieta-képleteknek nevezik. Ezeknek a képleteknek a bal oldali részei szimmetrikus polinomok az adott egyenlet x 1 , x 2 ..., x n gyökéből, a jobb oldali részek pedig a polinom együtthatójával vannak kifejezve.

2.6 Négyzetekre redukálható egyenletek (kétnegyedes)

A negyedik fokú egyenletek másodfokú egyenletekre redukálódnak:

ax 4 + bx 2 + c = 0,

bikvadratikusnak nevezzük, sőt, a ≠ 0.

Elég, ha ebbe az egyenletbe x 2 \u003d y-t teszünk, ezért

ay² + by + c = 0

keresse meg a kapott másodfokú egyenlet gyökereit

y 1,2 =

Az x 1, x 2, x 3, x 4 gyökök azonnali megtalálásához cserélje ki az y-t x-re, és kapja meg

x2 =

x 1,2,3,4 = .

Ha a negyedik fokú egyenletben x 1, akkor van gyöke is x 2 \u003d -x 1,

Ha x 3, akkor x 4 \u003d - x 3. Egy ilyen egyenlet gyökeinek összege nulla.

Példa :

2x 4 - 9x² + 4 = 0

Az egyenletet behelyettesítjük a kétnegyedes egyenletek gyökeinek képletébe:

x 1,2,3,4 = ,

tudva, hogy x 1 \u003d -x 2 és x 3 \u003d -x 4, akkor:

x 3,4 =

Válasz: x 1,2 = ±2; x 1,2 =

2.7 Biquadratic egyenletek tanulmányozása

Vegyük a bikvadratikus egyenletet

ax 4 + bx 2 + c = 0,

ahol a, b, c valós számok, és a > 0. Egy segédismeretlen y = x² beiktatásával megvizsgáljuk ennek az egyenletnek a gyökereit, és az eredményeket táblázatba írjuk (lásd 1. számú melléklet)

2.8 Cardano képlet

Ha modern szimbolikát használunk, akkor a Cardano képlet levezetése így nézhet ki:

x =

Ez a képlet határozza meg a harmadfokú általános egyenlet gyökereit:

ax 3 + 3bx 2 + 3cx + d = 0.

Ez a képlet nagyon nehézkes és összetett (több összetett gyököt tartalmaz). Nem mindig érvényes, mert. nagyon nehéz befejezni.

2.9 Harmadfokú szimmetrikus egyenletek

A harmadik fokú szimmetrikus egyenleteket alakegyenleteknek nevezzük

ax³ + bx² + bx + a = 0 ( 1 )

ax³ + bx² - bx - a = 0 ( 2 )

ahol a és b adott számokat, és a¹0.

Mutassuk meg, hogyan működik az egyenlet ( 1 ).

ax³ + bx² + bx + a = a(x3 + 1) + bx(x + 1) = a(x + 1) (x² - x + 1) + bx(x + 1) = (x + 1) (ax² +(b – a)x + a).

Azt kapjuk, hogy az egyenlet ( 1 ) ekvivalens az egyenlettel

(x + 1) (ax² +(b - a)x + a) = 0.

Tehát a gyökerei az egyenlet gyökerei lesznek

ax² +(b - a)x + a = 0

és x szám = -1

az egyenlet ( 2 )

ax³ + bx² - bx - a = a(x3 - 1) + bx(x - 1) = a(x - 1) (x² + x + 1) + bx(x - 1) = (x - 1) (ax 2 + ax + a + bx) = (x - 1) (ax² + (b + a)x + a).

1) Példa :

2x³ + 3x² - 3x - 2 = 0

Nyilvánvaló, hogy x 1 = 1, és

x 2 és x 3 a 2x² + 5x + 2 = 0 egyenlet gyöke,

Keressük meg őket a diszkrimináns segítségével:

x 1,2 =

x 2 \u003d -, x 3 \u003d -2

2) Példa :

5x³ + 21x² + 21x + 5 = 0

Nyilvánvaló, hogy x 1 \u003d -1, és

x 2 és x 3 az 5x² + 26x + 5 = 0 egyenlet gyöke,

Keressük meg őket a diszkrimináns segítségével:

x 1,2 =

x 2 \u003d -5, x 3 = -0,2.

2.10 Visszatérési egyenletek

Reciprok egyenlet - algebrai egyenlet

a 0 x n + a 1 x n - 1 + ... + a n - 1 x + a n \u003d 0,

amelyben a k \u003d a n - k, ahol k = 0, 1, 2 ... n, sőt, a ≠ 0.

A reciprok egyenlet gyökereinek megtalálásának problémája egy kisebb fokú algebrai egyenlet megoldásának problémájára redukálódik. A reciprok egyenletek kifejezést L. Euler vezette be.

Az alak negyedik fokának egyenlete:

ax 4 + bx 3 + cx 2 + bmx + am² = 0, (a ≠ 0).

Ennek az egyenletnek a formába hozása

a (x² + m²/x²) + b(x + m/x) + c = 0, és y = x + m/x és y² - 2m = x² + m²/x²,

ahonnan az egyenletet másodfokúvá redukáljuk

ay² + by + (c-2am) = 0.

3x 4 + 5x 3 - 14x 2 - 10x + 12 = 0

Ha elosztjuk x 2-vel, megkapjuk az ekvivalens egyenletet

3x 2 + 5x - 14 - 5 ×, ill

Hol és

3(y 2 - 4) + 5y - 14 = 0, innen

y 1 = y 2 = -2, tehát

És hol

Válasz: x 1,2 = x 3,4 =.

A szimmetrikus egyenletek a reciprok egyenletek speciális esetei. Korábban beszéltünk harmadfokú szimmetriaegyenletekről, de vannak negyedfokú szimmetriaegyenletek is.

Negyedik fokozatú szimmetrikus egyenletek.

1) Ha m = 1, akkor ez egy első típusú szimmetrikus egyenlet, amelynek alakja

ax 4 + bx 3 + cx 2 + bx + a = 0 és egy új behelyettesítéssel megoldva

2) Ha m = -1, akkor ez egy második típusú szimmetrikus egyenlet, amelynek alakja

ax 4 + bx 3 + cx 2 - bx + a = 0 és egy új behelyettesítéssel megoldva

2.11 Horner séma

A polinomok felosztásához a „szögosztás” szabályt vagy Horner-sémát alkalmazzuk . Ebből a célból a polinomokat csökkenő fokozatba rendezzük xés keressük meg a Q(x) hányados elsőbbségi tagját abból a feltételből, hogy ha megszorozzuk a D(x) osztó elsőbbségi tagjával, akkor megkapjuk a P(x) osztalék elsőbbségi tagját. A hányados talált tagját megszorozzuk, majd az osztóval, és kivonjuk az osztalékból. A hányados rangidős tagját abból a feltételből határozzuk meg, hogy az osztó felső tagjával megszorozva a különbségi polinom rangidős tagját adja, stb. A folyamat addig folytatódik, amíg a különbség mértéke kisebb lesz, mint az osztó mértéke (lásd a 2. számú mellékletet).

Az R = 0 egyenletek esetén ezt az algoritmust a Horner-séma helyettesíti.

Példa :

x 3 + 4x 2 + x - 6 = 0

Megtaláljuk a szabad tag osztóit ±1; ±2; ± 3; ±6.

Az egyenlet bal oldalát f(x)-el jelöljük. Nyilvánvaló, hogy f(1) = 0, x1 = 1. Osszuk el az f(x)-et x - 1-gyel. (Lásd a 3. számú mellékletet)

x 3 + 4x 2 + x - 6 \u003d (x - 1) (x 2 + 5x + 6)

Az utolsó tényezőt Q(x) jelöljük. Megoldjuk a Q(x) = 0 egyenletet.

x 2,3 =

Válasz : 1; -2; -3.

Ebben a fejezetben adtunk néhány képletet különféle egyenletek megoldására. A legtöbb képlet adott egyenletek megoldása. Ezek a tulajdonságok nagyon kényelmesek, mivel sokkal könnyebb az egyenleteket egy külön képlet segítségével megoldani, és nem egy általános elv szerint. Mindegyik módszerre adtunk egy bizonyítást és néhány példát.

Következtetés

Az első fejezetben a másodfokú egyenletek és a magasabb rendű egyenletek keletkezésének történetét tárgyaltuk. Több mint 25 évszázaddal ezelőtt különféle egyenleteket oldottak meg. Az indiai Babilonban sokféle megoldás született az ilyen egyenletek megoldására. Az egyenletek szükségessége volt és lesz.

A második fejezet különböző módszereket mutat be másodfokú egyenletek és magasabb rendű egyenletek megoldására (gyökkeresésére). Alapvetően ezek egy adott természetű egyenletek megoldására szolgáló módszerek, vagyis minden egyes egyenletcsoportra, amelyet valamilyen közös tulajdonság vagy típus egyesít, egy speciális szabály van megadva, amely csak erre az egyenletcsoportra vonatkozik. Ez a módszer (a saját képlet kiválasztása minden egyenlethez) sokkal könnyebb, mint a gyökerek megtalálása a diszkrimináns segítségével.

Ebben az esszében minden cél megvalósult, a fő feladatokat teljesítették, új, eddig ismeretlen formulákat bizonyítottak és tanultak meg. A példák sok változatát átdolgoztuk, mielőtt absztraktba foglalnánk őket, így már tudjuk, hogyan kell megoldani néhány egyenletet. Mindegyik megoldás hasznos lesz számunkra a további vizsgálatok során. Ez az esszé segített a régi ismeretek osztályozásában és az újak elsajátításában.

Bibliográfia

1. Vilenkin N. Ya. „Algebra 8. osztályhoz”, M., 1995.

2. Galitsky M.L. „Feladatgyűjtés az algebrában”, M. 2002.

3. Daan-Dalmediko D. „Utak és labirintusok”, M., 1986.

4. Zvavich L.I. „Algebra 8. osztály”, M., 2002.

5. Kushnir I.A. „Egyenletek”, Kijev, 1996.

6. Savin Yu.P. „Egy fiatal matematikus enciklopédikus szótára”, M., 1985.

7. Mordkovich A.G. „Algebra 8. osztály”, M., 2003.

8. Khudobin A.I. „Feladatok gyűjtése az algebrában”, M., 1973.

9. Sharygin I.F. „Algebra fakultatív kurzus”, M., 1989.

1. számú melléklet

Biquadratic egyenletek tanulmányozása

C	b		következtetéseket
C	b		Az ay² +by+c=0 segédegyenlet gyökein	Ennek az egyenletnek a gyökeiről a(x²)² +bx² +c=0
C< 0	b- bármilyen valós szám		y< 0 ; y > 0 1 2	x = ±Öy
C > 0	b<0	D > 0		x = ±Öy
		D=0	y > 0	x = ±Öy
		D< 0	nincsenek gyökerei	nincsenek gyökerei
	b ≥ 0			nincsenek gyökerei
			nincsenek gyökerei	nincsenek gyökerei
			y > 0 y< 0 1 2	x = ±Öy
C=0	b > 0		y=0	x=0
	b = 0		y=0	x=0
	b< 0		y=0	x=0

2. melléklet

Polinom osztása polinom "sarokkal"

A0	egy 1	a 2	...	a n	c
+
b 0 c	b 1 c	…	b n-1 c
B0	b 1	b 2	…	b n	= R (maradvány)

3. függelék

Horner séma

Gyökér
	1	4	1	-6	1
x 1 = 1
lebontani	5	6	0
	1	1×1 +4 = 5	5x1 + 1 = 6	6×1 - 6 = 0
gyökér
x 1 = 1

1. § A másodfokú egyenletek keletkezésének történetéből

2.11 Horner séma

Francois Viet francia matematikus fedezte fel a másodfokú egyenlet gyökereinek egy nagyon furcsa tulajdonságát. Ezt a tulajdonságot Vieta tételének nevezzük:

Tehát az x 1 és x 2 számok az egyenlet gyökerei:

ax² + bx + c = 0

Vannak identitásaink

Az egyenletet behelyettesítjük a kétnegyedes egyenletek gyökeinek képletébe:

C< 0

y< 0 ; y > 0

1 2

x = ±Öy

x = ±Öy

x = ±Öy

y > 0 y< 0

1 2

x = ±Öy

Talán érdekelni fogja